基于模糊-EKF模型的锂离子电池SOC联合估算

2021-08-16梅周盛夏靖武

客车技术与研究 2021年4期

周斌，梅周盛，陈林，夏靖武

(汉腾汽车有限公司，江西上饶 334000)

电池管理系统(BMS)作为电动汽车电池系统的关键控制单元，对电池系统的性能发挥起着至关重要的作用[1]。BMS中的一个核心功能指标SOC又是BMS设计中的重中之重。

目前SOC的估算方法主要有四类[2]，其中安时(Ah)积分法在工程应用中最为广泛，也是最基本的一种算法，但存在两个明显的缺陷：一是初始SOC值无法确定；二是累计误差无法消除[3]。基于电池特征参数法是依据开路电压(OCV)和SOC一对一的关系进行估算，但获取开路电压需要电池长时间静置[4]。基于数据驱动的方法主要包括神经网络、模糊神经等，这一类算法需要获取电池在不同情况下的各种数据，利用大量数据对模型进行训练以获取精准的SOC计算，这类方法依赖于获取电池大量数据，难度大，对芯片数据处理能力要求也高[5-7]。基于模型的估算方法主要有卡尔曼滤波法、粒子滤波法等，在建立精确的电池等效电路模型基础上估算SOC，其估算精度可以达到较好的效果，但对模型精度依赖较大[8-10]。可见使用单一的SOC算法很难获得满意的效果。

本文首先建立锂电池的二阶(以下简称2-RC)等效电路模型并进行参数识别，然后依据扩展卡尔曼滤波(EKF)算法建立SOC估算模型并进行验证和分析，最后基于模糊控制建立EKF、Ah积分、OCV的联合估算模型，实现SOC实时估算，避免单一算法的缺陷。

1 锂离子电池等效电路模型参数识别

1.1 锂离子电池等效电路模型

建立精确的锂离子电池等效电路模型是EKF估算SOC的基础，常用的等效电路模型[11-12]有：Rint、Thevenin、n-RC(n≥2)等。其中Rint和Thevenin等效电路模型结构清晰、运算简单，但是精度上n-RC等效电路模型(n≥2)更优，一定范围内n越大精度就越高，但n过大其精度反而会降低，工程应用也更复杂。综合考虑模型精度及工程应用，本文选择2-RC等效电路模型，如图1所示。

图1 2-RC等效电路模型

图中R0表示锂电池的欧姆内阻，R1C1、R2C2组成的电路用于描述锂电池内部的极化效应，电压源U(s)表示电池的OCV值，其与电池SOC有关。UL表示负载电压；I表示电流(充电时为正，放电时为负)。根据等效电路可以得到如下公式：

UL=U(s)-U0-U1-U2

(1)

(2)

通过式(1)、(2)和试验数据可对图1模型中R0、R1、R2、C1、C2进行参数辨识。

1.2 模型参数识别

锂离子电池可看作一个非线性动态系统，在不同SOC时通过对系统施加一个恒流脉冲信号，计算电池输出特性并加以识别，可以得到电池模型的各个参数。采用指数拟合的方法[13]进行参数识别计算。

图2 恒流脉冲电池电压变化曲线

(3)

式中：UOCV为开路电压;U1(t)、U2(t)分别为AB段R1C1、R2C2网络端的电压值。

在BCD区域，B点以后电池从放电状态转换为静置状态，当电流为零的一瞬间，电池电压会有一个跳变(即BC段的电压ΔU1)，这是由于欧姆内阻所致。根据ΔU1可计算出欧姆内阻R0=ΔU1/I。

(4)

对AB及CD段试验数据进行指数拟合，并联合式(3)、(4)可识别出R1、R2、C1、C2。按照相同方法可分别识别不同SOC下模型的上述参数值。

识别出上述参数后，通过Simulink建立仿真模型，以图3中工况循环数据对应的电流值作为仿真输入，得到电池端电压仿真结果，将其与试验值进行比较，如图4所示，结果表明：最大误差在40 mV以内，平均误差为2.01 mV，2-RC等效电路模型能较好地反映电池的动态特性。

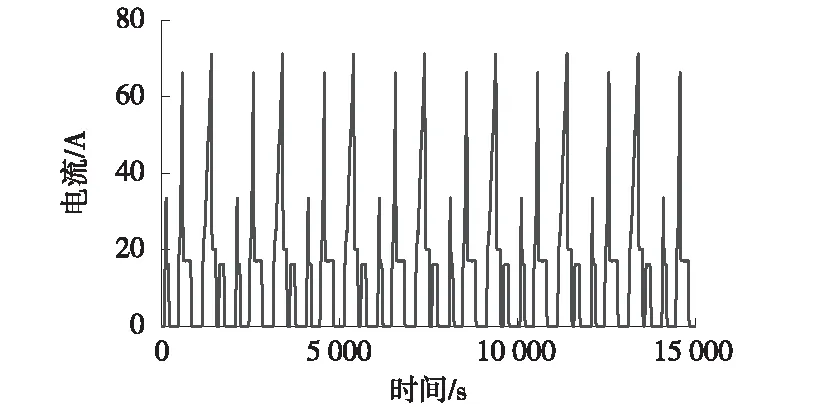
图3 工况电流曲线

图4 等效电路模型仿真值与试验值

2 EKF的锂离子电池SOC估算

2.1 EKF的SOC算法实现

EKF是针对非线性系统的一种滤波算法，将局部非线性化系统通过泰勒级数展开并去除高阶小量，以获取线性化系统，利用前一时刻的估算值和当前测量值进行递归推演，得到当前的最优估计值。利用EKF估算SOC时，其精度与电池模型精度、初始值、协方差矩阵均密切相关，特别是电池模型的精度。

EKF系统状态方程Xk和观测方程Zk如下：

Xk=AXk-1+Buk-1+wk-1，Zk=G(Xk，uk-1)+vk-1

(5)

式中：Xk为状态变量；uk-1为输入变量；Zk为观测变量；wk-1和vk-1分别为系统的随机输入噪声和观测噪声，wk-1和vk-1的方差与状态量初值无关，分别为Q和R。

根据电池等效模型计算公式(1)、(2)，RC网络计算公式(3)、(4)，以及Ah积分公式，得到系统状态及各个参数矩阵，如下：

(6)

(7)

(8)

式中U(s)为电池系统OCV，由试验数据通过MATLAB进行最小二乘法拟合，得到SOC的表达式。OCV的拟合精度直接关系到电池模型端电压的测量精度，因此也影响EKF对于SOC估算的精度。

确定好系统方程参数后，根据EKF步骤及递推公式，得到k时刻协方差矩阵Pk和增益矩阵Kk：

(9)

(10)

在MATLAB/Simulink中构建算法和模型，输入电池相关数据分别计算矩阵A、B、C和协方差矩阵P、增益矩阵K,并进行递推计算得到最终的估算结果，实现锂离子电池SOC的EKF估算。

2.2 EKF估算结果分析

使用50 Ah的锂离子电池测试数据，根据2.1中的计算方法进行EKF估算，选取常用的NEDC工况，设置EKF模型初始SOC为50%，得到如图5的SOC估算值，并与试验SOC真实值进行对比。

图5 EKF估算SOC结果

可以看出，EKF估算SOC在启动后300 s左右收敛到真实SOC值，此后的估算误差均较理想；当EKF收敛以后，SOC估算的误差在4%以内，并且当电流波动大导致残压变大或者呈现脉冲突变时，SOC误差也随之变大。

以上结果表明：二阶等效电路模型的EKF算法可以有效地进行SOC估算，并且收敛后的误差≤4%；等效电路模型的计算精度直接影响EKF估算的精度。

3 基于模糊控制的SOC联合估算

3.1 模糊控制联合估算模型的建立

从上述EKF方法及结果看，首先计算值需要一定的时间到达收敛，其次电池模型的精度直接影响估算精度。为解决EKF存在的此问题，利用模糊控制将EKF法、开路电压法和Ah积分法彼此联合，发挥各自算法的优势，建立联合估算算法对锂电池SOC进行估算。

本文采用Sugeno模糊控制系统模型[14-15]建立两个模糊控制器：①以BMS下电休眠时间Ts为输入，以开路电压SOC值SOCOCV的系数αOCV为输出的单输入单输出模糊控制器。②以运行时间Tr和单位周期内电流变化率ΔI作为输入，以EKF法的SOC值SOCEKF的系数βEKF作为输出的两输入单输出的模糊控制器。利用这个模糊控制器将EKF法、OCV法和Ah积分法进行联合，建立联合估算模型：

SOC0=αOCV·SOCOCV+(1-αOCV)·SOCold

(11)

SOCR=βEKF·SOCEKF+(1-βEKF)·SOCAh

(12)

式中：SOCAh为Ah积分法的SOC值；SOC0为初始SOC值；SOCR实时运行SOC值；SOCold为BMS内部储存的上次SOC值。

隶属度函数和规则是模糊控制器的关键，使用钟形函数。如图6所示，分别为单输入单输出系统中输入参数下电休眠时间Ts的隶属度函数曲线，两输入单输出系统中电流变化值ΔI和运行时间Tr的隶属度函数曲线。

图6 隶属函数曲线

参考实际电流的采样周期，以0.5 s时间间隔计算其时间的电流变化值ΔI。为确定不同ΔI对模型残压和EKF估算SOC的影响，将测试数据输入模型仿真，结果表明：当ΔI越小，模型残压越小且EKF估算SOC误差越小；当ΔI≥60 A后，模型残压和EKF估算SOC的误差值均保持在较高值，且几乎相同。故电流变化值ΔI的变化区间选取为(0，60 A)，运行时间区域选取为(0，5 000 s)，输出类型选用常数类型。ΔI选用Small、Mid、Big三个模糊语言进行描述，Tr用Short、Mid、Long三个模糊语言描述。结合图6，构建输出系数βEKF模糊规则，见表1。

表1 两输入单输出系统模糊规则

根据上述输入变量的隶属度函数和构建的模糊规则，最终系数αOCV和βEKF的输出控制图分别如图7和图8所示。在Simulink中将模糊控制器、EKF的SOC估算模块、Ah积分模块进行结合，用精准语言建立基于模糊控制的SOC联合估算模型，如图9所示。

图7 αOCV输出曲线

图8 βEKF输出曲线

图9 联合估算模型

图9所示的联合估算模型主要包括：SOC0计算模块、EKF计算模块、Ah积分计算模块以及模糊控制模块。SOC0计算模块用于计算初始SOC，先由模糊控制器确定系数αOCV，再根据该系数确定SOCOCV和SOCold的比例，进而计算出SOC0；EKF计算模块即为2.1中的EKF估算，是利用EKF法估算出电池SOCEKF；Ah积分模块利用Ah积分计算出SOCAh；模糊控制模块是将各个SOC计算模块进行联合。将试验数据代入联合估算模型中，可进行SOC联合估算。

3.2 模糊控制联合估算结果分析

将图10中实际采集的电流工况数据，代入3.1中所建立的SOC联合估算模型，得到联合估算SOC，并将其与EKF估算SOC和Ah积分SOC及真实SOC进行对比，如图11所示。

图10 NEDC工况实际电流激励曲线

图11 联合估算与安时积分、EKF估算结果对比

将三者估算值与真实试验SOC值进行对比得知：Ah积分法无法确定初始SOC值，整个计算过程一直无法消除误差；EKF法估算SOC在初始未收敛阶段估算误差较大；联合估算模型初始计算时通过模糊控制器计算系数αOCV，再根据式(9)结合SOCOCV和SOCold确定初始SOC值。实例中初始SOC的误差缩小到3%以内，较好的消除误差。

从联合估算SOC误差和EKF估算SOC误差曲线可知，联合估算最大误差为3.12%，EKF最大误差为3.92%，EKF估算时波动相对更大，这是因为模糊控制的联合估算法实时分配了SOCEKF和SOCAh的比例，减少了因电流波动造成的SOCEKF估算误差，整个过程相比于EKF，其SOC变化相对更加平滑，并且最大误差更小。