钢桥面板纵肋-顶板焊缝细节疲劳裂纹的应力强度因子分析
2021-08-15张启伟
李 丹 ,张启伟,姜 旭
(同济大学,上海市 200092)
0 引言
在焊接缺陷、应力集中、残余应力、车辆荷载反复作用等因素的影响下,疲劳问题成为制约正交异性钢桥面板发展的重要工程难题。U 肋-顶板焊缝一般从焊根或焊趾起裂,在疲劳裂纹穿透顶板、致使桥面防水层与铺装层损坏时才能发现,且检修困难,是正交异性钢桥面板中最为严重的疲劳病害[1]。近年来对于三维裂纹扩展模拟的研究不断发展,张高楠[2]以ANSYS 应力分析结果为基础,运用PATRAN及AGILE 模块首次对纵肋-顶板焊接模型进行3D断裂力学分析,对比认为简化为2D 模型会使分析结果过于保守。刘中祥[3]模拟了润扬大桥正交异性钢桥面板3 种典型细节的裂纹扩展过程,发现裂纹扩展相同长度时U 肋-顶板焊缝所需时间最短。黄云[4]等基于疲劳模型试验和理论研究,得出起始于顶板-纵肋焊根位置的裂纹属于Ⅰ型主导的复合型裂纹,裂纹面呈现出典型的空间曲面特征。既有研究对移动车载下U 肋-顶板焊缝焊根与焊趾处开裂模式的对比分析还不够深入系统。因此,本文以某钢箱梁斜拉桥为背景,建立正交异性钢桥面板节段模型与U 肋-顶板连接细节子模型,通过有限元方法计算移动车辆荷载下裂纹尖端的应力强度因子,对萌生于焊趾与焊根处的裂纹以及三种开裂模式进行对比研究。
1 扩展有限元方法
本文对于应力强度因子的研究基于ABAQUS 中的扩展有限元模块。扩展有限元法(XFEM)通过引入富集函数来描述不连续的位移场[5]。位移函数表示为:
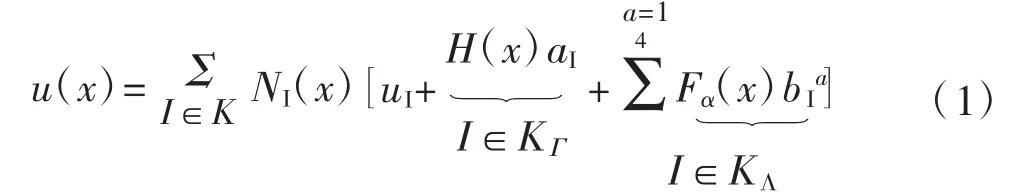
式中:NI(x)为常用的节点位移函数;uI是连续节点位移向量;aI是被分割单元的附加自由度;bIa是裂纹尖端单元的附加自由度;KΓ为被裂纹贯穿单元节点的集合;KΛ为裂尖单元节点的集合;H(x)是表示裂纹不连续位移场的跳跃函数,其表达式为:
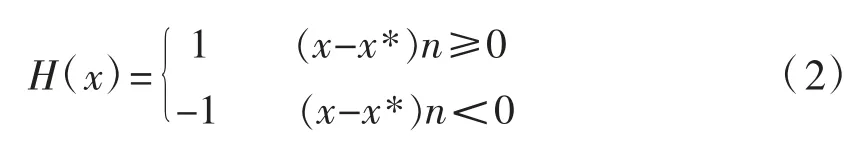
式中:x 为积分点;x*为裂纹面上最靠近的点;n 为外法线单位向量。
式(1)中最后一项Fα(x)为裂纹尖端渐进函数,描述裂尖位移,其表达式为:
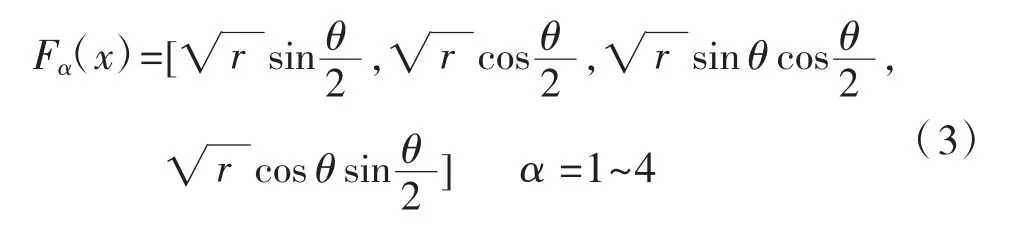
式中:(r,θ)表示裂纹尖端的极坐标。
扩展有限元法中裂纹面独立于网格存在,不需要与单元边界重合;在裂纹扩展过程中无需对裂纹尖端进行网格重划分;对网格密度要求较低,计算效率高,可以有效处理不连续问题。
2 钢箱梁节段有限元模型的建立
2.1 模型参数
以某千米级钢箱梁斜拉桥为项目背景,桥梁横截面车道示意见图1,由于17 号U 肋处于重车轮迹线下方,经实桥检测其疲劳病害也更为严重,故选择17 号U 肋的U 肋-顶板连接处作为关注部位,车辆横向加载以重车轮迹线为基准。
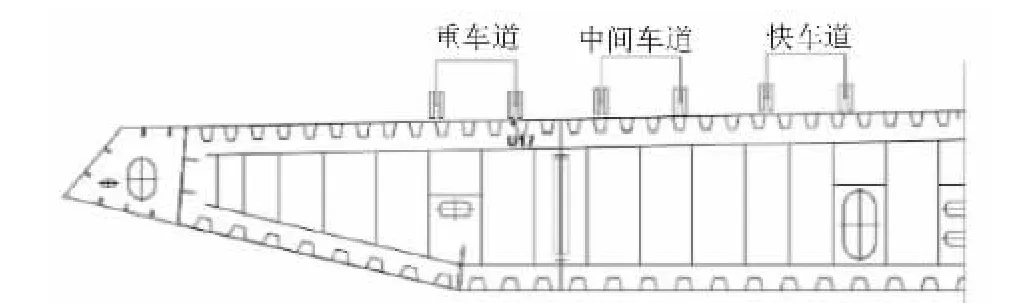
图1 横截面示意图
利用ABAQUS 有限元软件建立16 m 标准梁段的钢箱梁模型。依据实桥材料与尺寸,钢箱梁梁高4 m,顶板厚14 mm,U 肋厚8 mm,横隔板厚10 mm;钢材种类为Q345qD,弹性模量2.1×105MPa,泊松比0.3;钢桥面板U 肋与顶板间采用全熔透焊缝连接,焊脚尺寸为8 mm。
采用壳-实体耦合的建模方式,壳单元类型选用S4R,实体单元类型选用C3D8R。整体模型纵桥向端部采用固结约束,横向端部采用对称约束,由于本文关注点处于节段跨中位置,依据圣维南原理,上述边界条件对有限元计算结果影响较小。钢箱梁有限元模型见图2。
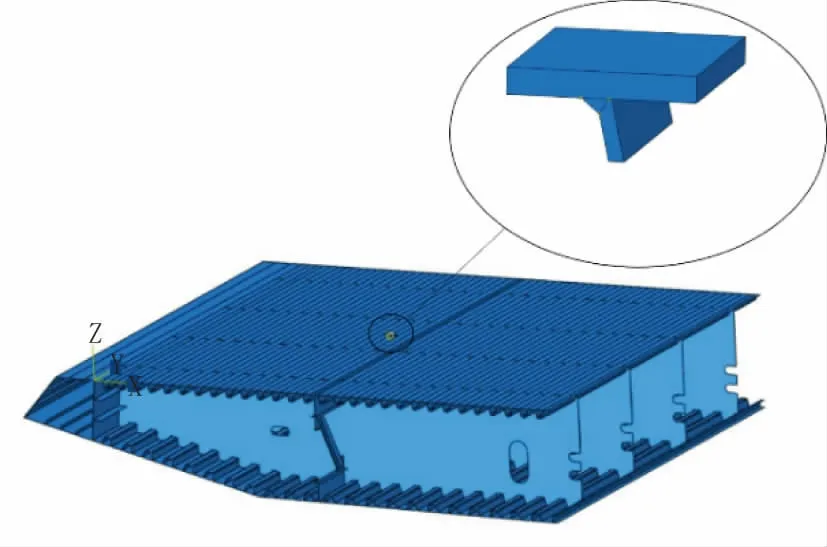
图2 钢箱梁有限元模型
钢箱梁整体网格尺寸为200 mm;U 肋-顶板连接细节的精细实体模型大小为100 mm×100 mm×40 mm(长×宽×高),网格尺寸为2 mm;在U 肋-顶板连接细节实体模型的焊根与焊趾处分别嵌入长轴为10 mm,深度方向2.5 mm 的半椭圆形裂纹。
2.2 加载方式
加载车辆选用《公路钢结构桥梁设计规范》(JTG D64—2015)中的疲劳荷载模型Ⅲ[6],见图3、图4。疲劳荷载模型Ⅲ由4 个标准轴组成,纵向前后两轴组间距较大(6 m),故而可以忽略叠加效应,同时为简化计算,本文仅考虑纵向轴距为1.2 m 的双轴轮载作为疲劳荷载。单车轮着地面积为200 mm×600 mm,偏于安全地不考虑桥面铺装的扩散效应。
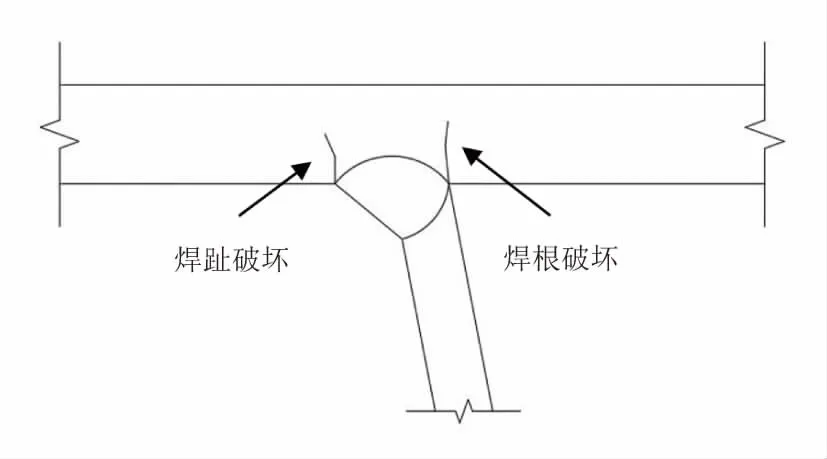
图3 U 肋-顶板焊缝疲劳破坏类型
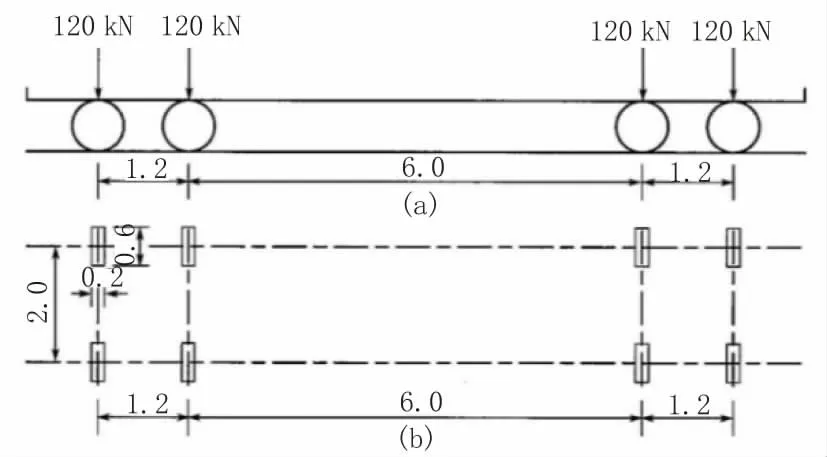
图4 疲劳破坏模型Ⅲ(单位:m)
使用FORTRAN 语言编写DLOAD 子程序在ABAQUS 中实现移动加载,设定横纵向移动步距均为200 mm(纵向中心处增加一个工况)。根据车轮位置横向分布概率模型,车轴偏离中心大于0.8 m 的概率几乎为零[6],故横向偏移中心轮迹线不超过0.8 m,共设9 个工况;纵向考虑横隔板的阻断作用,共设55个工况。加载工况布置见图5。
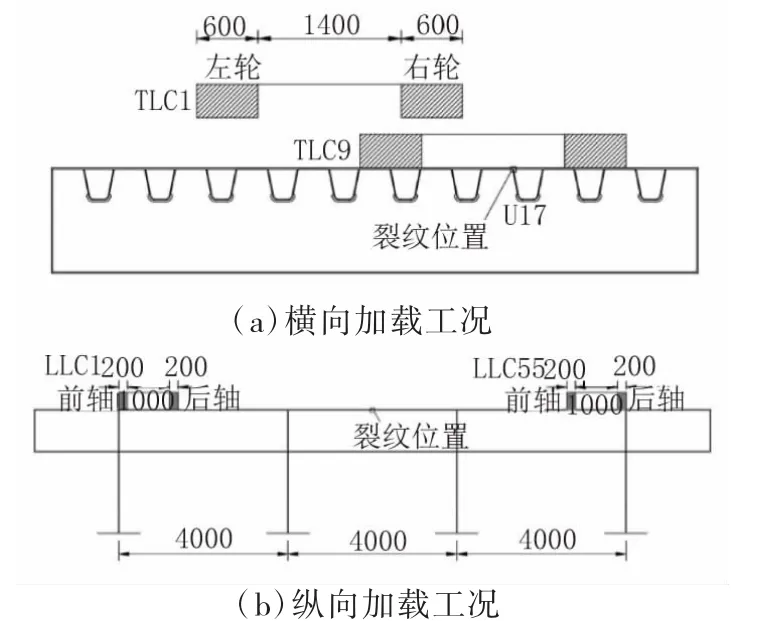
图5 车辆荷载工况(单位:mm)
3 应力强度因子分析
断裂力学将裂纹分为Ⅰ型裂纹(张开型裂纹)、Ⅱ型裂纹(滑开型裂纹)Ⅲ型裂纹(撕开型裂纹),KⅠ、KⅡ、KⅢ分别对应三种开裂模式的裂纹应力强度因子。采用2.2 所述的加载方式,提取裂纹尖端沿厚度方向中点的应力强度因子,设置15 道围线积分,取积分稳定后值。
(1)三种开裂模式的应力强度因子影响线
U 肋-顶板连接细节焊趾与焊根处裂纹尖端应力强度因子影响线见图6~图8。结果表明:
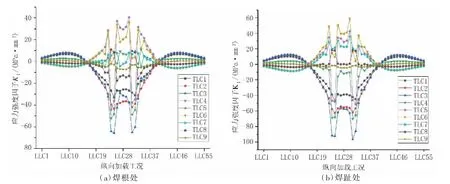
图6 应力强度因子影响线(单位:MP a·mm1/2)
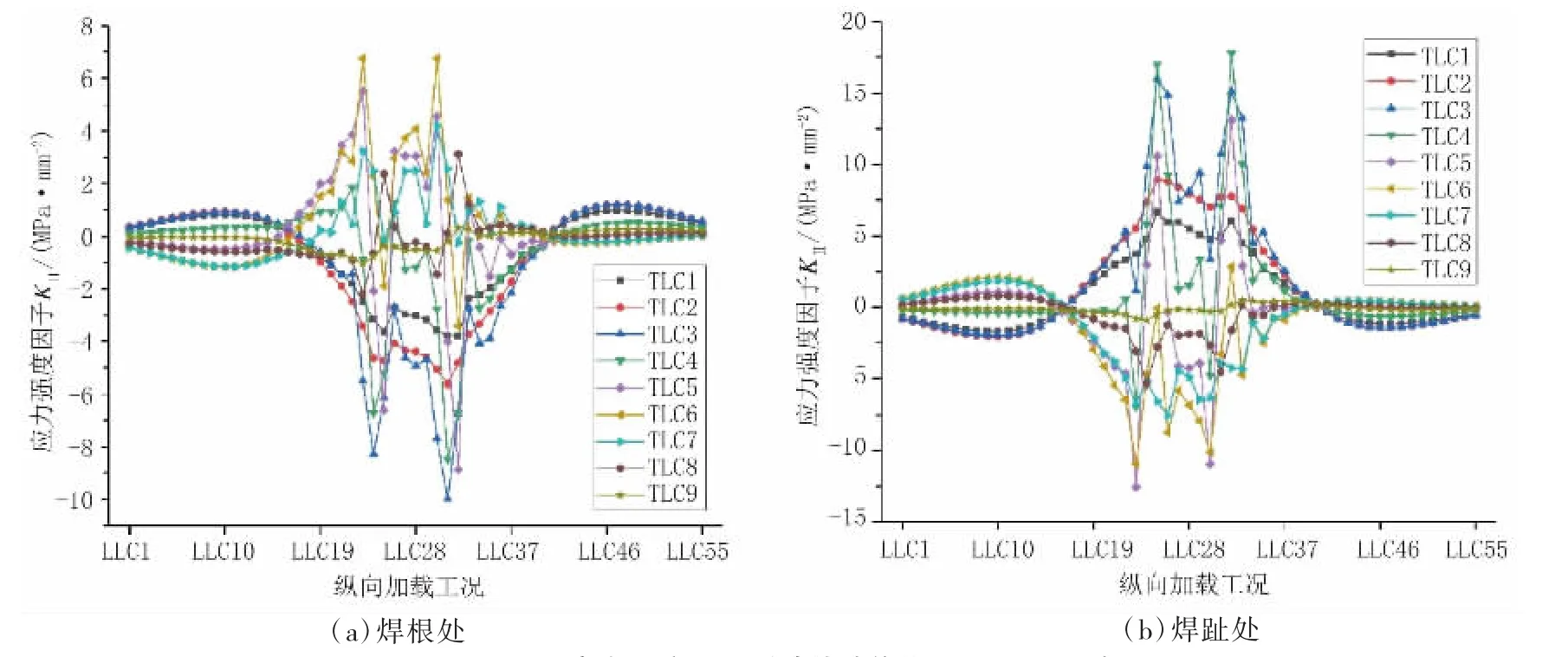
图7 应力强度因子影响线(单位:MP a·mm1/2)
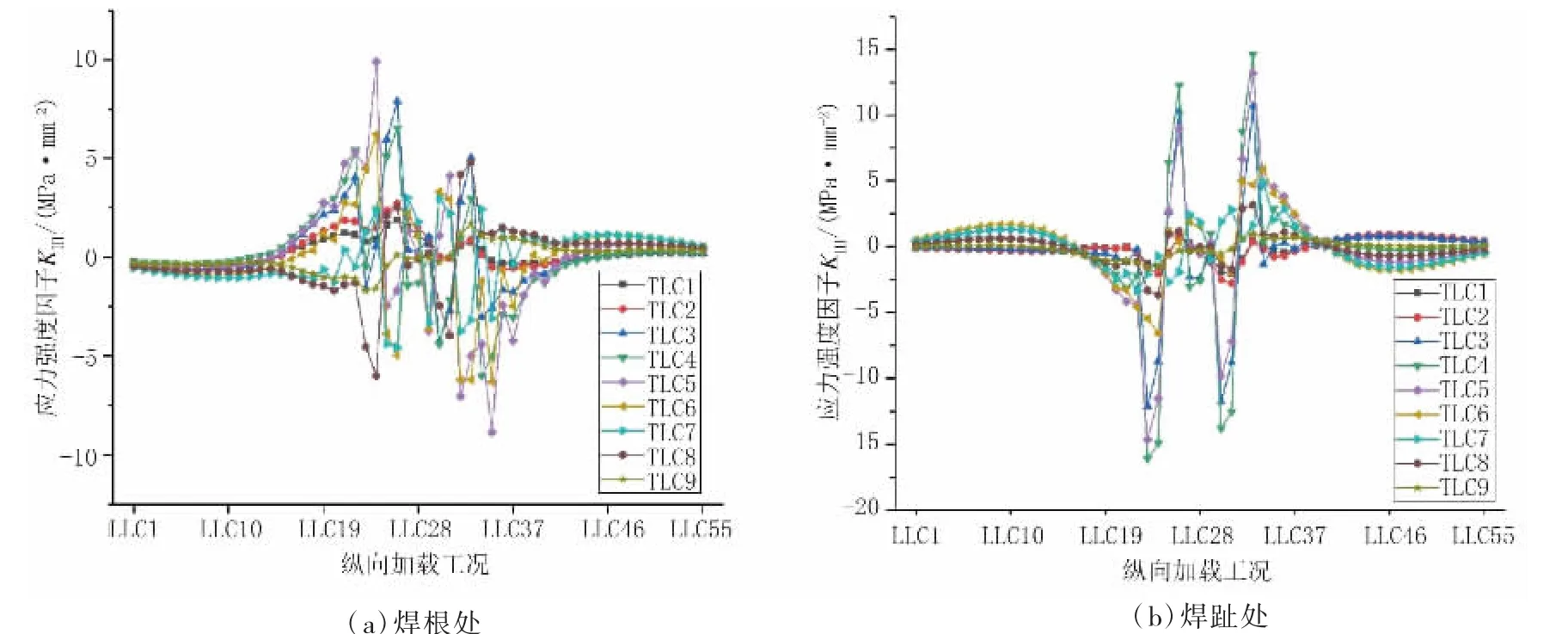
图8 应力强度因子影响线(单位:MP a·mm1/2)
a.焊趾处裂纹的应力强度因子KⅠ、KⅡ、KⅢ的最大值均略大于焊根处裂纹的应力强度因子最大值,且在横向工况的中心位置(车轮位于裂纹正上方)时达到最大值;
b.在应力强度因子关于纵向加载工况的折线图中,应力强度因子KⅠ在关于y 方向呈轴对称形态,应力强度因子KⅢ则关于y 方向呈反对称形态;
c.车轴纵向位于中心位置及附近,车轮横向位于裂纹右侧时,焊根处KⅠ、KⅡ为正;焊趾处KⅠ为正,车轮横向位于裂纹左侧时,焊根KⅠ、KⅡ为负;焊趾处KⅠ为负,KⅡ为正。
(2)三种开裂模式的应力强度因子对比
U 肋-顶板连接细节中,焊趾与焊根处纵向中心位置的加载工况下,裂纹尖端应力强度因子KⅠ、KⅡ、KⅡ的横向影响线见图9;横向中心位置的加载工况下,裂纹尖端应力强度因子KⅠ、KⅡ、KⅡ的纵向影响线见图10。结果表明:
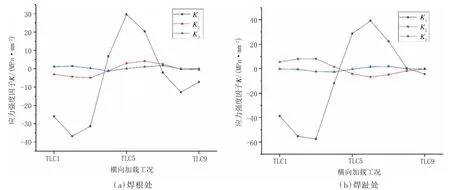
图9 纵向中心位置的应力强度因子(单位:MP a·mm1/2)
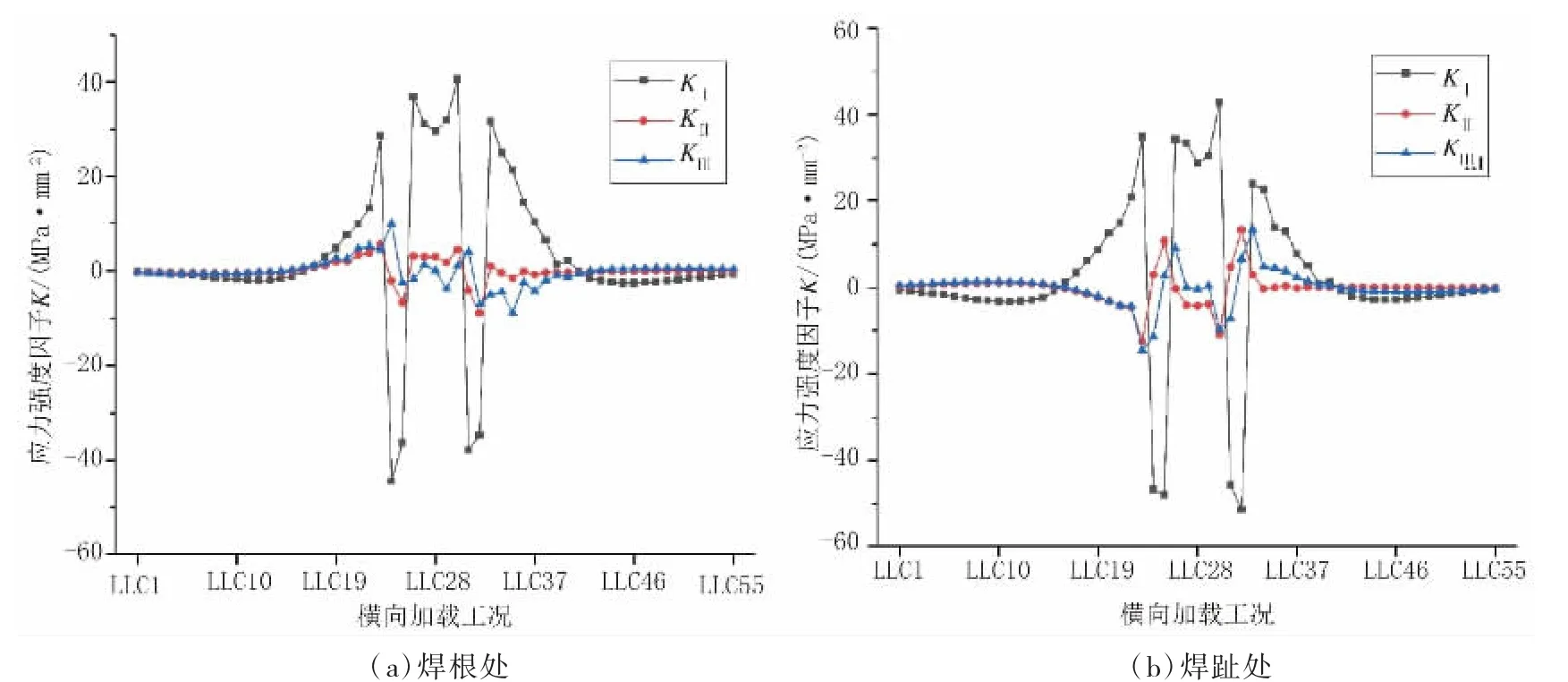
图10 横向中心位置的应力强度因子(单位:MP a·mm1/2)
a.焊根与焊趾处裂纹的应力强度因子KⅠ在三种应力强度因子中所占比重最大,Ⅰ型(张开型)裂纹在U肋-顶板焊接部位的复合型疲劳裂纹中占主导地位;
b.纵向位于中心位置,横向在车轮位于裂纹正上方(TLC5 及附近的工况)时,KⅠ为正,达到最大值;
c.横向位于中心位置,纵向在裂纹位于两车轴中间(LLC28 及附近的工况)时,KⅠ为正,达到最大值;而在纵向车轮位于裂纹正上方时,KⅠ为负,裂纹受压闭合。
4 结语
本文基于ABAQUS 扩展有限元法,以某千米级斜拉桥为工程背景,建立钢箱梁标准节段模型,对正交异性钢桥面板纵肋-顶板连接细节疲劳裂纹的应力强度因子进行了分析。根据文中的计算结果,得出如下结论:
(1)焊趾处三种裂纹应力强度因子的最大值均略大于焊根;车辆荷载下,焊趾与焊根处的裂纹尖端应力强度因子具有相似规律,与的值则呈现相反的规律。
(2)钢箱梁中萌生于纵肋-顶板连接细节的疲劳裂纹是以Ⅰ型裂纹为主导的Ⅰ-Ⅱ-Ⅲ复合型裂纹;在横向车轮位于裂纹正上方,纵向裂纹位于两车轴中间时,裂纹扩展驱动力最大。
(3)在疲劳车辆纵向驶过裂纹所在位置的约2 m范围内时,应力强度因子(以Ⅰ型为主)发生较大波动,出现最大值与最小值,对疲劳裂纹的发展产生较大影响。
