顾及海底地形非线性项的最小二乘配置反演方法

范 雕，李姗姗，欧阳永忠，孟书宇，陈 成，邢志斌，张 驰

1.地理信息工程国家重点实验室，陕西 西安 710054；2.信息工程大学地理空间信息学院，河南 郑州 450001；3.南京信息工程大学遥感与测绘工程学院，南京 210044；4.32022部队，湖北 武汉 430074；5.海军工程大学导航工程系，湖北 武汉 430074；6.航天工程大学，北京 102206

21世纪是海洋的世纪，海洋是我国经济社会发展的重要的战略空间，在国家政治、经济、科技、军事发展的全局中日益突出。海洋测绘是实施国家海洋战略的前瞻性、基础性、公益性事业，是海洋开发管理、权益维护、科学研究和国防安全等的重要基础。目前海洋测绘已经成为我国推进科技兴海，壮大海洋经济，建设海洋强国不可或缺的技术支撑[1]。

作为海洋测绘的重要内容，海底地形测量绘制的全球海底地形图在科学研究、国民经济和国防建设等方面占据着极其重要的位置：从科学层面，海底地形在很大程度上反映了潜在的地质作用[2]，影响海啸波的传播和相关海啸模型的建立[3]，以及海洋环流等的相关研究[4]；从应用层面，海底地形图的绘制不仅可保障航道与航运安全，也可为深海潜器的地形辅助惯性匹配导航提供先验的背景场模型，为深海多传感器组合精确导航提供又一种可选择的技术手段。

目前，基础水深数据获取技术主要包括船基声呐测深技术、机载激光雷达测量技术(airborne LiDAR bathymetry)、海岸带一体化地形测量技术、潜基海底地形测量技术等。然而，上述海深测量手段相对全球海洋而言，不仅测区范围有限、测量效率较低，而且测量结果数据分布很不均匀。特别是随着海洋测绘工作测量范围从近海浅水区向大洋深水区不断发展，囿于测量平台限制，船基和潜基测量方式将难以有效满足远洋全球测绘需求。采用船基深海测绘将花费200多船年(ship-years)时间，耗费大量人力物力才能绘制完成[5]。

随着空间对地观测技术的发展，目前卫星测高技术已成为获取全球海洋观测信息的主要手段之一，依托测高卫星获取的全球海面高数据可恢复全球海洋重力场信息。根据地壳均衡理论，海底地形起伏及其均衡补偿物质的密度异常分布将会引起海面重力场的变化，这意味着海面重力场信息与海底地形在一定程度上具有某种对应的相关性关系，它们之间的相关性关系使得利用地球重力场构建深海海域大尺度的海底地形成为可能。利用海面重力场信息反演海底地形，国内外学者提出并验证了多种反演算法，如重力地质方法[6-8]、SAS方法[9,10]、导纳函数方法[11-13]等。其中，基于Parker公式[14]的导纳函数方法是依据地形求解重力场级数形式的线性反解，该反演算法涉及诸多地球物理参数求解(准确的地球物理参数对反演结果影响明显)。SAS方法基于导纳函数理论研究了反演波段海底地形和重力数据线性比例关系，进而获取地形-重力比例因子，巧妙地回避了导纳函数方法中地球物理参数的求解难题[15]。文献[16—17]引入回归分析技术改进了SAS方法比例因子解算流程，取得了良好的计算效果。然而，无论是SAS方法和回归分析方法，还是导纳函数方法均回避了非线性项对反演结果的影响，仅仅考虑了海底地形和海面重力信息之间的线性成分，因而必定会影响最终反演结果的准确性。关于海底地形反演高次项问题，国内外学者也进行了多方面尝试。文献[18]在顾及地壳挠曲均衡状态下，利用卫星测高重力异常、大地水准面高、船测水深等数据(考虑输入数据误差影响)，在空域上利用最小二乘迭代反演方法并顾及高次项影响进行了模拟仿真试验。文献[19]依据卫星测高重力异常数据、船测重力异常数据和船测水深数据，采用非线性最小二乘反演技术构建了新西兰海域考虑高次项影响的海底地形模型(称为RW99模型)；然而空域最小二乘迭代方法涉及非线性算子求解等，过程复杂、烦琐且计算效率很低。文献[20]以航空重力梯度数据为输入，采用SA(simulated annealing)方法尝试解决高次项问题，但是SA方法需不断调整和完善函数参数方可获得目标函数全局最优解，计算速度十分有限，不利于推广应用。文献[21]运用频率域迭代方法在中国南海部分海域开展试验，探索解决反演高次项难题的途径和手段，该方法计算效率高，并取得了较好的试验效果。

综上所述，针对目前反演方法常未顾及非线性项影响和目前反演高次项研究进展，本文提出了顾及海底地形非线性项的最小二乘配置(least-squares collocation，LSC)反演方法。首先，利用Earth2014地形位模型研究目标海区地形统计特征，进而解算目标海区局部协方差函数最佳参数；尔后，基于局部最佳协方差函数解算相关信号的自协方差矩阵和互协方差矩阵。然后，以卫星测高重力异常和重力异常垂直梯度为输入，采用最小二乘配置技术构建兼顾海底地形和海面重力线性趋势项和非线性项影响的海底地形模型。最后，将反演模型与国际广泛使用的S&S V18.1和ETOPO1等海深模型进行比对分析，同时引入功率谱密度和相干性等指标评估反演海深模型效能。

1 原理与方法

1.1 最小二乘配置原理

依据Parker公式[14]，海底地形与海面重力异常频率域的表达式为

F(Δg(x,y))=2πG(ρc-ρw)e-2πf·d·

(1)

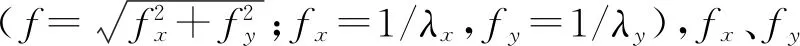
F(Δgz(x,y))=2πG(ρc-ρw)e-2πf·d·

(2)

式中，F(Δgz(x,y))表示重力异常垂直梯度Δgz(x,y)的傅里叶变换，其余参数意义同上。当仅考虑式(1)和式(2)中线性项影响时，即所谓重力导纳函数

(3)

由式(3)可知，当仅考虑式(1)和式(2)中的线性项影响时，重力异常和重力异常垂直梯度经向下延拓等处理后与海底地形呈线性关系。文献[16]基于此线性关系，采用回归分析方法推估相应波段的海底地形

(4)

式中，α、αz和β、βz分别表示线性回归的比例因子和常数项。据以上分析可知，式(4)算法模型实质是式(1)和式(2)的线性近似，忽略了算法中非线性项影响。然而，文献[23]和笔者前期研究表明，虽然式(1)和式(2)线性部分对海面重力信息贡献占主要，但是直接忽略非线性项的贡献势必造成有效信息的浪费，特别在地形起伏较大的区域，地形高次项对海面重力信息贡献明显。借鉴最小二乘配置理论基本原则，将式(1)和式(2)中级数形式分为线性和非线性两部分：线性部分表示函数模型系统性参数，是结果的主要影响部分，称为整个算法模型的趋势项部分；非线性项部分代表函数模型随机性参数，为整个算法模型的信号部分，反映与趋势不符的小的变化，即扣除趋势项后的残余项部分，如图1所示。

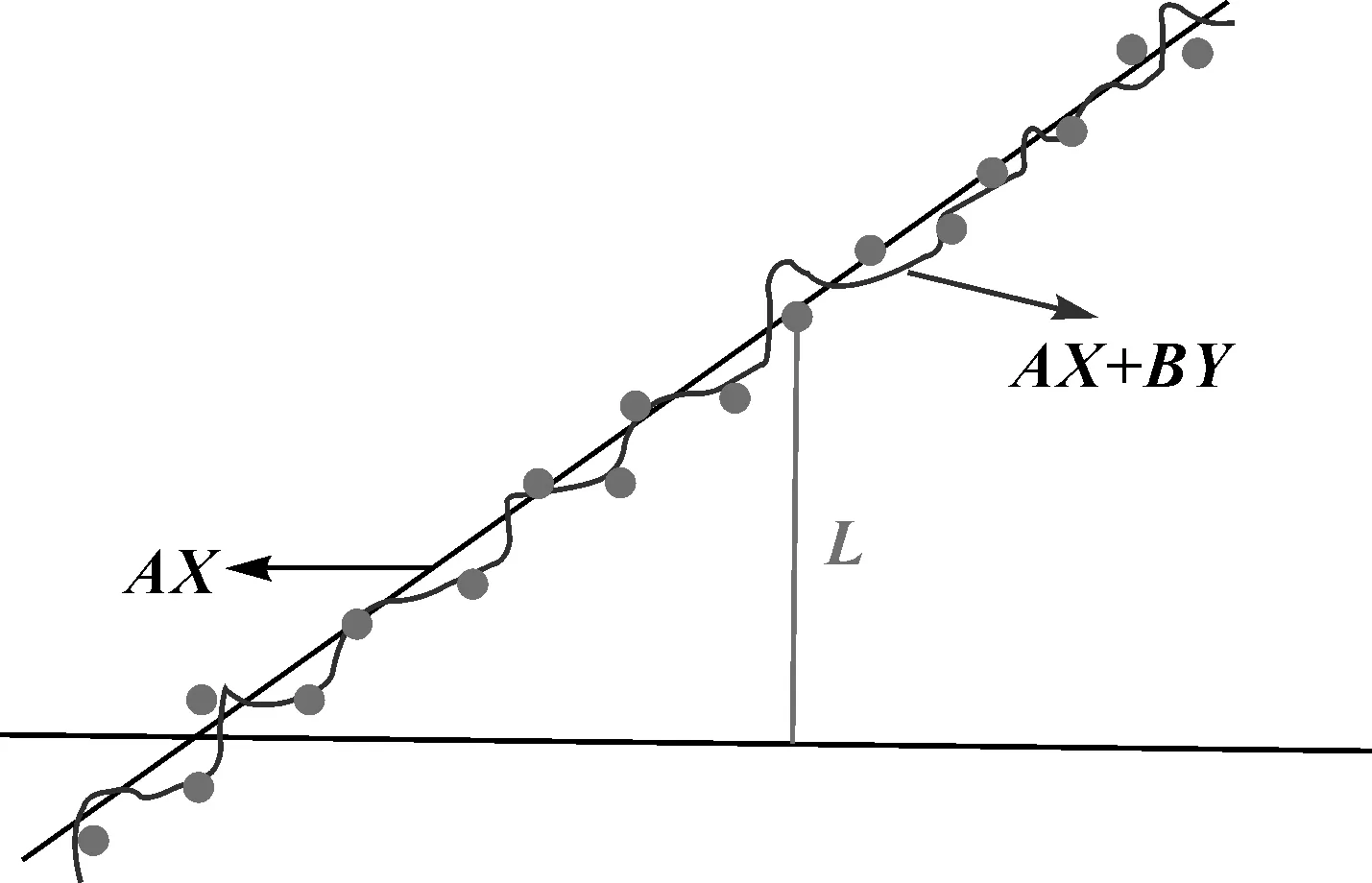
图1 最小二乘配置Fig.1 Least square collocation

图1中圆点表示观测值L，实线表示经回归分析处理后得到的观测值拟合直线，为观测值的趋势项部分，简称为AX；曲线为顾及观测值与趋势项AX不符的小的变化而拟合生成的曲线，曲线函数表达式为AX+BY，其中BY代表与趋势项不符的小的变化。显然，当顾及与趋势项不符的小的变化时生成的曲线将更加合理。基于以上分析，引入最小二乘配置理论中信号部分，则式(4)表示为

(5)

式中，s表示函数模型的信号部分，代表函数模型非线性项(可认为是扣除趋势项后的残余地形部分)对结果影响，从而依据式(5)可实现对线性模型的修正和完善。式(5)观测方程的矩阵形式为

L=AX+s+Δ

(6)

式中，L为海底地形观测值向量；A为系数矩阵；X表示参数矩阵；s为信号向量；Δ表示观测值误差向量，各量具体形式为

(7)

将式(6)表示为最小二乘配置的函数模型为

L=AX+BY+Δ

(8)

式中，B和Y具体表达式为

(9)

式中，In为n阶单位阵；S代表显信号(已测点残余地形信号)；S′表示隐信号(未测点残余地形信号)。式(8)对应的误差方程为

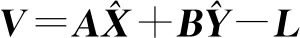
(10)

最终，式(10)最小二乘配置解为

(11)

式中，C表示相应的协方差矩阵，如CL和Css分别代表观测值和显信号的协方差矩阵。

1.2 局部地形协方差函数

协方差函数是有效实施统计分析的基本依据，合理的协方差函数应充分反映区域数据的变化规律和相关性，良好的协方差函数能得到较好的计算结果；反之，若协方差函数并非区域数据的有效表征，则将会歪曲解算结果。因此确定协方差函数之于最小二乘配置尤为重要。囿于客观原因限制，通常依托经验协方差函数获取区域协方差矩阵。设距离为l，从数学角度分析可知，经验协方差函数为相关函数，同时应满足以下3条规则[24]：①距离l为零时，相关性为正，C(0)=C0>0；②协方差函数为偶函数，C(-l)=C(l)；③距离l为零时，相关性最强，C(0)≥C(l)，当且仅当l=0时，等号成立。同时满足以上3个条件的协方差函数为强相关协方差函数。本文选择以下强相关协方差函数作为经验协方差函数。

(1)Moritz协方差函数

(12)

(2)Inverse协方差函数

(13)

(3)Gauss协方差函数

C(l)=C0·e-a2l2

(14)

式中，C0是两点距离为零对应的协方差函数值，表示协方差函数的变化幅度；l为两点之间距离；a为常数。

综上，利用研究海域离散海深测量数据、卫星测高重力异常数据和重力异常垂直梯度数据，采用最小二乘配置技术构建海底地形格网数值模型步骤可概括为：

(1)获取海底地形反演波段范围。依据设计的高通、低通滤波器和挠曲波长、海区海深内在联系，结合海底地形影响重力信息有限波段特点和先期研究成果，确定研究海域利用重力数据反演海底地形有效波段范围。

(2)获取残余海底地形信息。依托先验海底地形模型和卫星测高重力异常数据，采用最小二乘技术获得地形与重力数据趋势项信息，然后扣除先验海底地形模型中地形与重力趋势项部分，进而获取残余海底地形信息。

(3)确定目标海区局部协方差函数。研究分析目标海域残余海底地形统计特征，依据最小二乘拟合方法解算局部协方差函数未知参数，从而得到能够较好反映目标海域地形特征的局部协方差函数，进而获取相关信号的自协方差矩阵和互协方差矩阵。

(4)获取反演波段重力信息和非反演波段海底地形。利用设计的高通、低通和带通滤波器对系统输入数据(离散船测点和重力数据)实施滤波操作，得到相应波段的重力和海底地形信息。

(5)海底地形数值模型构建。利用获取的研究海域信号协方差矩阵以及反演波段输入数据信息，采用最小配置方法构建反演波段海底地形；然后叠加反演波段和非反演波段海底地形，进而得到最终海底地形数值模型。

基于以上分析，利用稀疏船测数据、卫星测高重力异常和重力异常垂直梯度数据，采用最小二乘配置技术构建海底地形格网数值模型整体设计路线如图2所示。

图2 最小二乘配置路线Fig.2 Inversion scheme of least square collocation

2 数值试验分析

2.1 数据准备与前期处理

选择日本海某1°×1°(133.5°E—134.5°E，38°N—39°N)海域开展研究试算工作，其中数据来源如下：

(1)卫星测高重力数据(包括重力异常和重力异常垂直梯度数据)来源于SIO，UCSD(Scripps Institution of Oceanography,University of California,San Diego)，V24.1版本，分辨率为1′，卫星测高重力资料统计结果见表1。

表1 研究海域重力数据统计Tab.1 Gravity data statistics of the research sea area

(2)研究海域船测多波束和单波束数据来源于NGDC(The National Geophysical Data Center)发布的研究海区实测数据，共收集到研究海域2228个船测数据。

依托船基方式利用声学测量仪器对研究海域实施点、线和面测量，囿于导航条件和仪器等方面因素影响，原始海深测量结果中难免存在粗差。因此本文采用S&S V18.1海深模型作为先验海深模型对原始海深测量数据进行质量控制：

(1)采用双线性插值技术将S&S V18.1海深模型值内插到原始海深测量点处得到模型内插值。

(2)将模型内插值与原始海深测量值作差得到海深残差值。

(3)将3倍残差标准差设置为阈值，把海深残差绝对值大于阈值的船测点予以剔除，从而得到经3σ原则简单处理后的海深数据。

原始海深数据、海深残差和处理后的海深数据统计结果见表2，其中括号内为船测海深点数。

表2 海深数据统计结果Tab.2 Statistical results of bathymetric data m

由表2可知，海深残差值标准差为88.09 m，从而剔除粗差的阈值设置为264.27 m。最终剔除了67个粗差可疑点，占船测点总数的3%左右，得到2161个船测数据。依据前期研究可知，重力异常或者重力异常垂直梯度长波段信号主要受地壳均衡影响，短波段高频重力信息受向下延拓因子和观测噪声影响严重[25]，因此利用重力异常或者重力异常垂直梯度数据仅可恢复有限波段海底地形信息，非反演波段地形信息通常采用船测海深数据恢复[10-11,15,26-28]。据此，从2161个船测数据中随机挑选1659个数据作为控制点，用于补偿非反演波段海底地形信息，控制点个数约占总测深点数的76.77%；剩余502个船测点作为评价最终海深模型构建的检核点待用。研究海域控制点和检核点空间分布如图3所示，其中白色六边形表示控制点，黑色三角形代表模型评估待用的检核点，背景图为S&S V18.1海深模型。

2.2 输入数据滤波

分别选择合适的高通和低通滤波器对重力数据进行滤波处理，以抑制重力数据长波和短波部分信息对海底地形反演结果的影响。选择的高通滤波器和低通滤波器为

(15)

式中，τ和ζ为滤波参数。高通滤波器W1(fx,fy)可有效去除长波段信号的影响。SIO学者在利用SIOV20.1重力异常数据构建S&S V15.1海深模型过程中，取参数ζ=3891 km4参与数据滤波计算，不同平均海深d对应的低通滤波器和不同波长对应的低通滤波器(1-W1(fx,fy))形状分别如图4(a)实线和虚线所示。

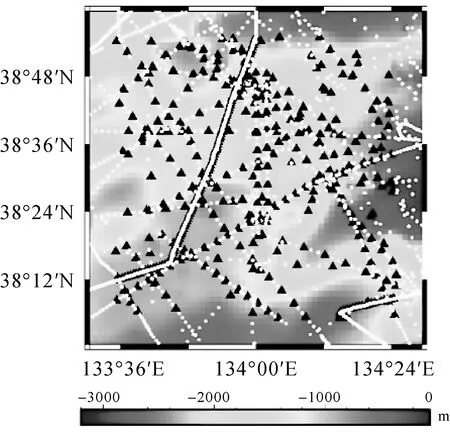
图3 控制点和检核点分布Fig.3 The distribution of control points and checkpoints

地壳均衡补偿将地壳描述为漂浮在流体岩浆表面的弹性薄板，具备抵抗地质载荷导致薄板产生形变的能力。也就是说，地壳弹性厚度类似低通滤波器能够抵消短波段地质体影响。当地形波长较长超过弹性板能够抵消波长的极限，弹性板将发生形变，产生地壳均衡补偿效应。弹性板能够抵抗的地形极限波长值，称为挠曲波长。不同厚度的弹性板对应不同的挠曲波长，而利用重力数据反演海底地形需尽量抑制地壳均衡补偿对地形-重力信息的干扰，尽量使用重力信息中的地形“成分”。综合均衡响应函数[25]和式(15)可得不同弹性厚度对应挠曲波长如图4(b)所示。有效弹性厚度分别为3、5、10和15 km时，对应的发生挠曲补偿现象的波长为120、160、200和250 km。

因研究海区平均海深为1.31 km(船测海深平均值)，由图4(a)低通滤波器与海深和滤波波长的关系可得滤波波长范围大约在10～13 km，结合文献[15]和文献[29]最终短波段截断波长选择为15 km。另外为有效抑制地壳均衡补偿对海面重力信息的影响，充分利用卫星测高重力信息中的地形分量，依据文献[30]认为研究海域有效弹性厚度为5 km，然后根据有效弹性厚度与波长的关系(图4(b))，长波段截断波长最终选择为160 km。从而试验海域利用卫星测高重力数据反演海底地形的反演波段范围为15～160 km。采用合适的带通滤波器(式(15)高通滤波器和低通滤波器乘积)获得的反演波段重力数据数值统计结果见表3。

图4 滤波器Fig.4 Filter

表3 反演波段重力数据统计Tab.3 Statistics of gravity data of inversion waveband

2.3 选取协方差函数

利用研究海域稀疏离散控制点和相关重力场信息，基于最小配置方法构建海底地形格网数值模型过程中，待求隐信号为格网海底地形值趋势项的小变化，显信号是控制点残余海底地形信息(扣除趋势项)。依据最小二乘配置理论可知，信号与观测值间通过协方差函数相联系，合理的协方差函数一直是最小二乘配置中的关键问题。因研究对象的几何和物理特性决定了其内部相关性，从而确定协方差函数时，需充分考虑这些特性以正确反映研究对象的这种相关性。

据此，本文选择Earth2014地形模型[31]作为先验海底地形模型统计分析目标海域空间属性特征，基于对研究海域海底地形特征的充分描述和表达，从而解算协方差函数的合理参数以获取研究海域相关量的协方差矩阵。Earth2014为WAGG(Western Australian Geodesy Group)发布的一套球谐系数模型，包括全球地形(Earth’s topography)、岩石等效地形(rock-equivalent topography)、地球形状(Earth’s shape)和地形位模型(implied topographic potential)。Earth2014格网数据包含1′和5′两个分辨率版本，球谐系数(spherical harmonic coefficients)最高阶次为10 800阶。构建Earth2014系列模型数据来源如下：

(1)南极洲基岩(bedrock)、冰厚(ice thickness)和海深数据来源于Bedmap2，如图5暗红色区域所示。

(2)格林兰基岩地形数据(bedrock topography)由GBT(Greenland Bed Topography)V3提供，如图5红色区域所示。

(3)海洋、主要内陆湖泊和北半球高纬度陆地地形(除格林兰外)数据源自SRTM30_PLUS V9，对应图5蓝色区域和黑色区域。

(4)纬度±60°之间的所有陆地数据来自于SRTM V4.1 Topography，对应图5黄色区域。

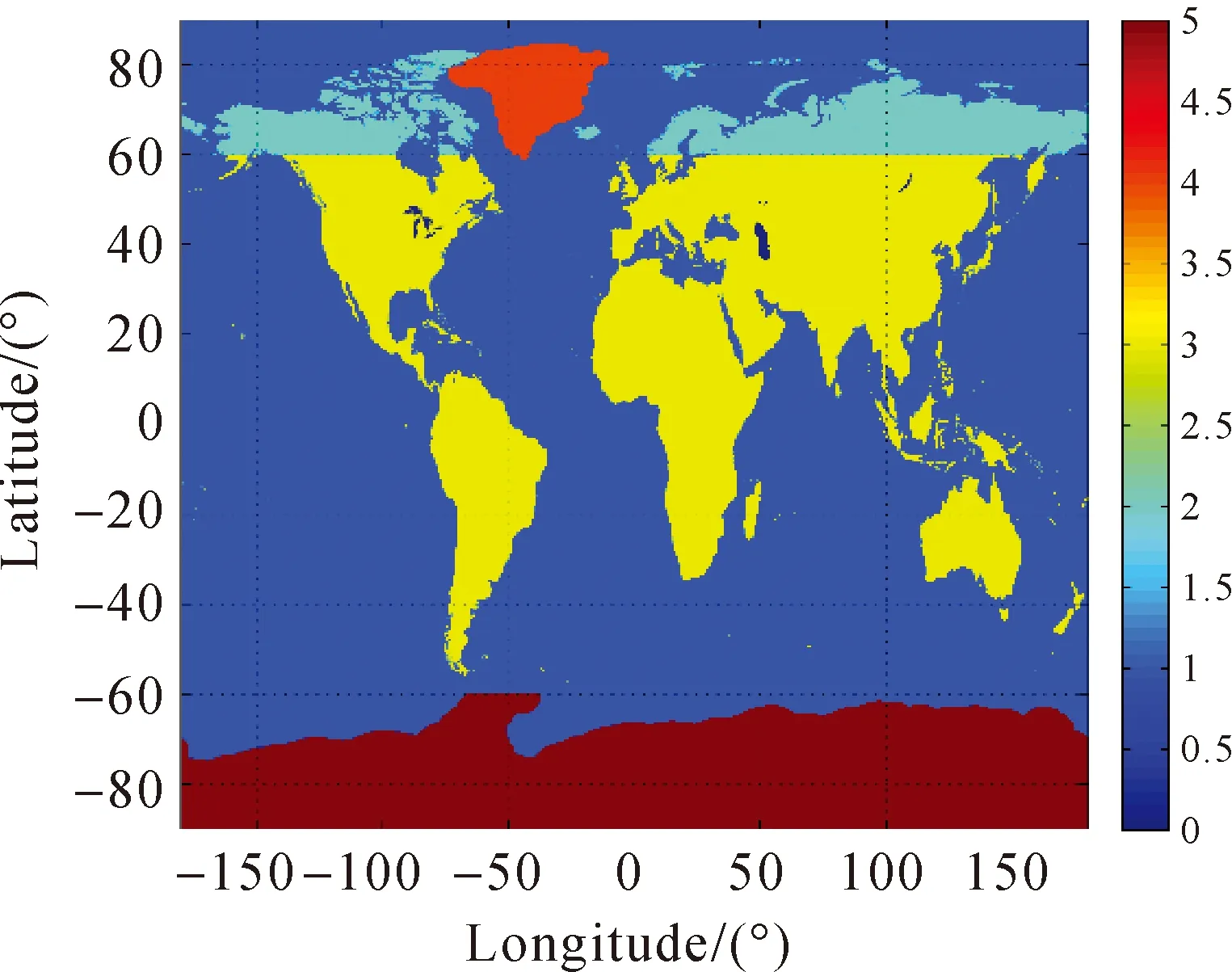
from http:∥ddfe.curtin.edu.au/图5 Earth2014输入数据空间分布Fig.5 Distribution of data in Earth2014

Bedmap2、GBTV3、SRTM30_PLUS V9和SRTM V4.1数据融合过程详见文献[31]。最终，Earth2014提供了地球上主要冰盖(ice sheet)最新的基岩和地形信息以及海洋深度格网信息。同时为满足不同应用需求，Earth2014模型包括如下几个类型：①地球物理表面(the physical surface，SUR)；②基岩(bedrock，BED)，即不考虑地球上水和冰的影响；③地形、基岩和冰(topography bedrock and ice，TBI)，即不考虑地球上水的质量；④冰盖厚度(ice sheet thickness，ICE)；⑤岩石等效地形(rock-equivalent topography，RET)，即将冰层和水层“压缩”为等效岩石厚度。根据本文研究需要，选择BED类型的地形位系数模型，称为Earth2014.BED2014.1min.geod。利用地形位系数模型求解地形(高度起算面为平均海平面)公式如下

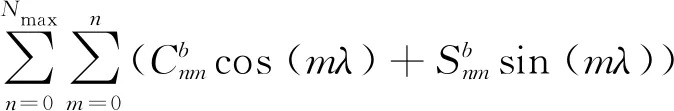
(16)

为使研究区域残余地形统计协方差充分表达研究区域地形特征，需充分且有效地利用研究区域数据。从而利用TEarth2014_Res模型统计研究海域残余地形协方差时，统计范围设置为研究区域最大经度缩小20′，最小纬度增大20′所形成的正方形格网，即有效距离最大为40′。基于以上分析，顾及协方差函数非负特点，研究海域共得到残余地形协方差统计值26组。其中距离为零时，协方差C0为0.043 km2，相关长度为6′左右(C0/2对应的距离)。采用最小二乘方法拟合各个局部协方差函数参数，依据式(12)、式(13)和式(14)可得目标海域Moritz协方差函数、Inverse协方差函数和Gauss协方差函数分别为

(17)

2.4 海底地形模型构建

利用最小二乘配置方法构建海底地形模型中显信号为控制点反演波段残余海底地形信息。本文获取显信号方法是：将事先挑选的1659个控制点格网化得到格网化海深；然后对格网化海底地形施以带通滤波操作，进而得到反演波段海底地形信息；凭借SIOV24.1重力异常数据，采用最小二乘配置方法获得地形和重力异常趋势项地形信息，进而通过扣除地形趋势项得到残余地形；然后采用双线性插值技术将残余海底地形内插到控制点处，从而得到控制点残余海底地形。囿于插值方法限制，若控制点处于边缘位置将导致插值失败，因此为保证插值过程顺利完成，将控制点范围沿经度和纬度方向分别内缩2′，最终得到1409个控制点。利用目标海域局部经验协方差函数(Moritz协方差函数、Inverse协方差函数和Gauss协方差函数)解算得到相应的显信号协方差矩阵，以及隐信号和显信号互协方差矩阵。分析易知，当显信号间距离很近时，对应的协方差矩阵表现极强奇异性，因而为克服显信号协方差矩阵奇异难题，考虑到研究区域海深测量数据质量，依据S-44(4th)海道测量标准中三等测量估计测量水深精度，当水深d(研究海域平均水深)选择1 296.40 m时，船测海深观测精度(协方差)为890.07 m2。借鉴文献[37—38]的处理方法，将Moritz协方差函数、Inverse协方差函数和Gauss协方差函数解算得到的显信号协方差矩阵与海深观测值方差之和代入参与计算。

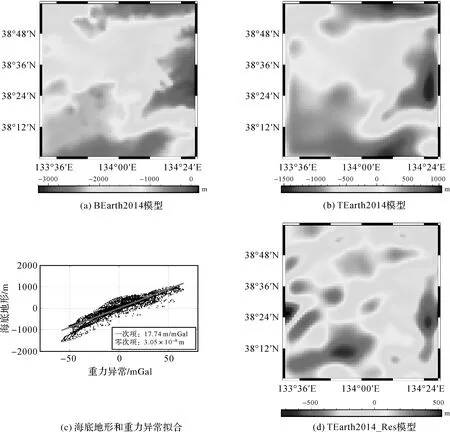
图6 Earth2014相关模型Fig.6 Earth2014 relevant models

最终以卫星测高重力异常和重力异常垂直梯度数据为数据输入，基于最小二乘配置技术，分别采用研究海域Moritz协方差函数、Inverse协方差函数和Gauss协方差函数构建的海深模型结果如图7和图8所示，分别称为BAT_DG_Moritz模型、BAT_DG_Inverse模型、BAT_DG_Gauss模型、BAT_VGG_Moritz模型、BAT_VGG_Inverse模型和BAT_VGG_Gauss模型。依据3种协方差函数解算得到的海底地形趋势项的常数项和一次项参数和利用最小二乘拟合获得的常数项和一次项参数结果见表4。可以看出，基于Gauss协方差函数计算得到的最小二乘配置方法中趋势项部分与最小二乘拟合参数差别明显；Moritz协方差函数和Inverse协方差函数趋势项解算结果与最小二乘方法解算结果最为接近。利用最小二乘方法计算得到的地形与重力数据(重力异常和重力异常垂直梯度)线性项参数，分别构建相应的海深模型。其中以重力异常为输入建立的海深模型称为BAT_DG_LS模型，利用重力异常垂直梯度构建的海深模型称为BAT_VGG_LS模型，效果如图9所示。可以看出，利用最小二乘方法构建的海深模型与采用最小二乘配置方法建立的海深模型均能反映研究海域地形概貌，但是与最小二乘配置方法反演的海底地形存在明显差异，如在研究海域西部两类模型存在明显不符。究其原因，最小二乘配置顾及地形和重力二者线性趋势关系的同时，也包含了对二者线性趋势变化的反映，结果更加合理可信。

2.5 海底地形模型分析评估

考察评价利用卫星测高重力数据，采用最小二乘配置方法建立的海深模型精度和效能，引入目前国际上广泛使用的ETOPO1模型、GEBCO模型、SIO系列模型之S&S V18.1模型以及文献[39]利用重力异常垂直梯度采用SAS(Smith and Sandwell)方法反演的BAT_VGG海深模型参与模型比对评估环节，各海深模型统计结果见表5。由于本文反演模型建立过程中涉及时频转换，从而为消除边缘效应影响，将最终反演结果分别沿经度和纬度方向内缩5′参与统计。

图7 重力异常构建海深模型结果Fig.7 Bathymetry inversion using gravity anomaly

图8 重力异常垂直梯度构建海深模型结果Fig.8 Bathymetry inversion using vertical gravity gradient anomaly

图9 最小二乘方法构建海深结果Fig.9 Bathymetry inversion using least square

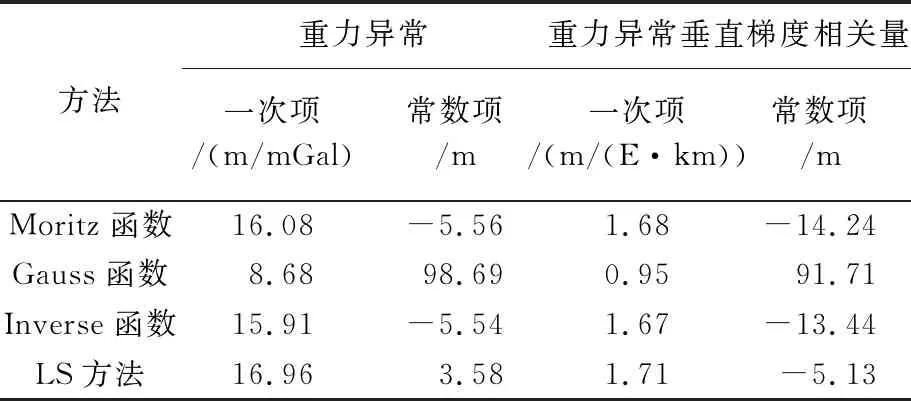
表4 LSC和LS趋向性参数解算结果Tab.4 Parameters of the leaner term calculated by LSC and LS

从表5可以看出，研究海域海深模型中水深最浅约为400 m，最大水深为3000 m左右。以重力异常和重力异常垂直梯度为输入，采用相同残余地形协方差函数，依据最小二乘配置方法反演得到的海深模型(如BAT_DG_Moritz和BAT_VGG_Moritz、BAT_DG_Inverse和BAT_VGG_Inverse等)统计参数(最大值、平均值和相关系数等)结果相近，对应的海深模型相关程度高达0.999。以BAT_DG_Gauss和BAT_VGG_Gauss模型为例，两海深差值最大值、最小值，平均值和标准差分别为33.15、-33.30、-0.61和8.02 m，两海深模型相关系数高达0.999 9，两模型表现状况与采用的反演方法有关。与其余海深模型比对发现，采用最小二乘方法获取的趋势项海深模型BAT_VGG_LS和BAT_DG_LS模型最大水深约为2300 m，明显浅于其余海深模型统计结果；与ETOPO1、GEBCO和S&S V18.1等海深模型相关程度也低于利用最小二乘配置反演海深结果，说明了顾及非线性趋势项能明显提高反演模型地形表达效果。海深模型间相关系数显示，BAT_VGG模型与ETOPO1模型和GEBCO模型相关系数为0.93，ETOPO1模型与GEBCO模型相关系数为0.92左右，而本文采用最小二乘配置方法反演海深模型与其余海深模型相关系数均超过了0.95，进一步说明了本文反演海深模型与目前发布的海深模型均能够较好附和，验证了本文反演方法的可行性。以502个检核点作为外部检核条件检验海深模型精度(海深模型值通过相应的内插函数内插到检核点处，并与检核点处实测海深值进行比对)，定义海深模型相对精度为检核均方差值与检核点平均海深(取正值)之比，海深模型检核统计结果见表6。

表6海深模型检核统计结果显示，以重力异常为输入，采用最小配置方法建立的海深模型各统计指标(最大值、最小值和均方差等)结果相近。仔细对比各海深模型检核统计结果发现，本文最小二配置反演模型检核平均值绝对值达到了111 m左右，回归分析方法建立的BAT_DG_LS和BAT_VGG_LS检核平均值分别约为91和75 m，BAT_VGG模型、ETOPO1模型和GEBCO模型也分别约为50、22和35 m。一般检核平均值应该在零值附近或量级较小，这时再去考虑其他指标，如标准差和均方差等才更合适。产生该现象(检核平均值偏离零值较大)的原因，笔者认为是反演模型中存在系统误差所致，若能有效约束系统误差影响，则反演模型质量可较大幅度提升，例如文献[40]利用质量较好的稀疏实测数据对反演模型进行校正，从而削弱了系统误差的影响。本文采用在海深模型基础上加上模型检核平均值的方法以削弱系统误差影响，削减系统误差后的各海深模型检核统计结果见表7，海深模型括号内的数为参与统计的有效检核点数。需要说明的是，由于检核统计指标如标准差、均方差等可能受粗差或异常值的影响较大，因此在统计过程中若检核点差值处于阈值(设置为3倍标准差和平均值之和)之外，则认为是粗差或异常值并予以剔除，例如BAT_DG_Moritz模型和BAT_DG_LS异常值点数分别有15个和4个，有效检核点分别有487个和498个。

比对表6和表7结果可以发现，各海深模型除去系统差和异常值后统计指标改善明显。利用最小二乘配置方法反演的海深模型检核差值平均值由百米量级下降到3 m范围内；BAT_DG_LS和BAT_VGG_LS检核差值平均值也分别从91.86 m和74.82 m降低到4.79 m和5.06 m，S&S V18.1模型检核平均值下降为0.82 m，说明了模型系统误差得到了有效削弱。系统误差削弱后，各模型检核均方差也大幅改善，BAT_DG_Moritz和BAT_VGG_Moritz等采用最小二乘配置建立的海深模型检核精度从约127 m提高到50 m以内，精度提升达到了2.5倍到4倍左右；而BAT_DG_LS和BAT_VGG_LS扣除系统差和检核点异常值后，检核精度提升有限，仅提高了4%左右；BAT_VGG、ETOPO1、GEBCO和S&S V18.1模型检核精度分别提高33%、15%、10%和34%左右。

表7统计结果显示，输入依据为重力异常或者重力异常垂直梯度时，Moritz协方差函数构建的BAT_DG_Moritz模型和BAT_VGG_Moritz模型检核精度略高于基于Gauss函数和Inverse函数反演得到的海深模型。仔细考察使用不同重力数据和相同协方差函数反演海深检核统计结果可以发现，采用相同协方差函数反演海深结果中，利用重力异常获取的海深结果优于重力异常垂直梯度反演海深结果。另外，基于最小二乘配置采用不同重力源构建的海深模型检核插值与检核点相关系数均达到了0.99以上，与检核点相关程度强于ETOPO1、GEBCO和BAT_VGG模型，与S&S V18.1模型相当；同时本文利用最小二乘配置反演海深模型相对精度在3.8%以内，与S&S V18.1模型相当，远远优于其余海深模型。

观察比对本文利用最小二乘方法和最小二配置方法构建的海深模型结果发现，利用最小二乘方法构建的海深模型检核精度远低于最小二配置结果，如以重力异常为输入数据，采用最小二乘方法建立的BAT_DG_LS模型，检核均方差为171 m左右，而利用最小二乘配置方法构建的海深模型检核精度最低为50 m左右，相比BAT_DG_LS模型精度提高了2.5倍左右；BAT_VGG_LS模型检核均方差值为215 m左右，而基于最小二乘配置使用重力异常垂直梯度构建的海深模型检核精度最低为50 m左右，相比BAT_VGG_LS精度提升了约近3.5倍；同时BAT_DG_LS和BAT_VGG_LS模型不仅检核差值绝对值最大值均超过了500 m，而且相对精度也均超过了13%。据前计算结果可知，采用Moritz协方差函数和Inverse协方差函数获取的趋势项参数与最小二乘方法解算结果较为接近，可是最终反演海深结果中诸多统计指标均逊于最小二乘配置反演海深结果，因此进一步说明了顾及反演算法中非线性项影响的必要性和本文反演方法的有效性。本文利用最小二乘配置反演海深模型的检核差值标准差在45 m左右，BAT_VGG模型、ETOPO1模型和GEBCO模型检核标准差均接近或者超过了百米。综合对比各海深模型，海深模型检核均方差统计结果中，S&S V18.1模型检核精度最高，检核结果为40 m左右，本文利用最小二乘配置构建的海深模型效能与之相当。进一步验证了反演海底地形时顾及非线性项影响的重要性以及最小二乘配置解决反演非线性问题的有效性。

选择利用最小二配置方法反演海深检核精度最高的BAT_DG_Moritz模型和BAT_VGG_Moritz模型参与进一步研究各海深模型在目标海域表现情况，分析不同检核差值范围内检核点占比结果如图10所示。

从不同检核差值检核点数量占比结果(图10(a))可以看出，S&S V18.1模型、BAT_DG_Moritz、BAT_VGG_Moritz和ETOPO1模型在差值绝对值小于大约50 m以内的检核点数量占比较多；特别是S&S V18.1模型、BAT_DG_Moritz模型和BAT_VGG_Moritz模型差值小值数量明显多于其余模型；而本文BAT_DG_Moritz模型和BAT_VGG_Moritz模型又优于S&S V18.1模型；其中，GEBCO模型差值小值数量占比较少。图10(a)结果还表明，各海深模型检核差值超过200 m后不同差值对应的检核点数量已很少。各个海深模型不同检核差值范围检核点占比情况如图10(b)所示。考察图10(b)可以发现，BAT_DG_Moritz模型和BAT_VGG_Moritz模型不同检核差值范围检核点比例曲线走势几乎一致，导致该现象与最小二乘配置方法本身机理有关。S&S V18.1模型、BAT_DG_Moritz模型和BAT_VGG_Moritz模型在不同检核差值范围检核点比例远远高于其余模型；BAT_VGG模型在检核点比例小于60%左右时，检核点占比均小于ETOPO1模型；GEOCO模型相对于其余模型表现欠佳，在差值大于150 m左右后，GEOCO模型检核差值比例与ETOPO1模型近乎一致。检核点占比80%时，S&S V18.1模型、BAT_DG_Moritz模型和BAT_VGG_Moritz模型检核差值最大值仅约为42 m，ETOPO1模型和GEBCO约为150 m，BAT_VGG模型约为107 m；检核差值100 m范围内BAT_DG_Moritz模型和BAT_VGG_Moritz模型检核点数量占比约93%，ETOPO1模型约占73%，GEBCO模型约占55%，BAT_VGG模型约占79%，S&S V18.1模型达到了96%左右。由此可见，S&S V18.1模型、BAT_DG_Moritz和BAT_VGG_Moritz模型在目标海域表现最佳，其余海深模型检核差值绝大多数在200 m范围内。

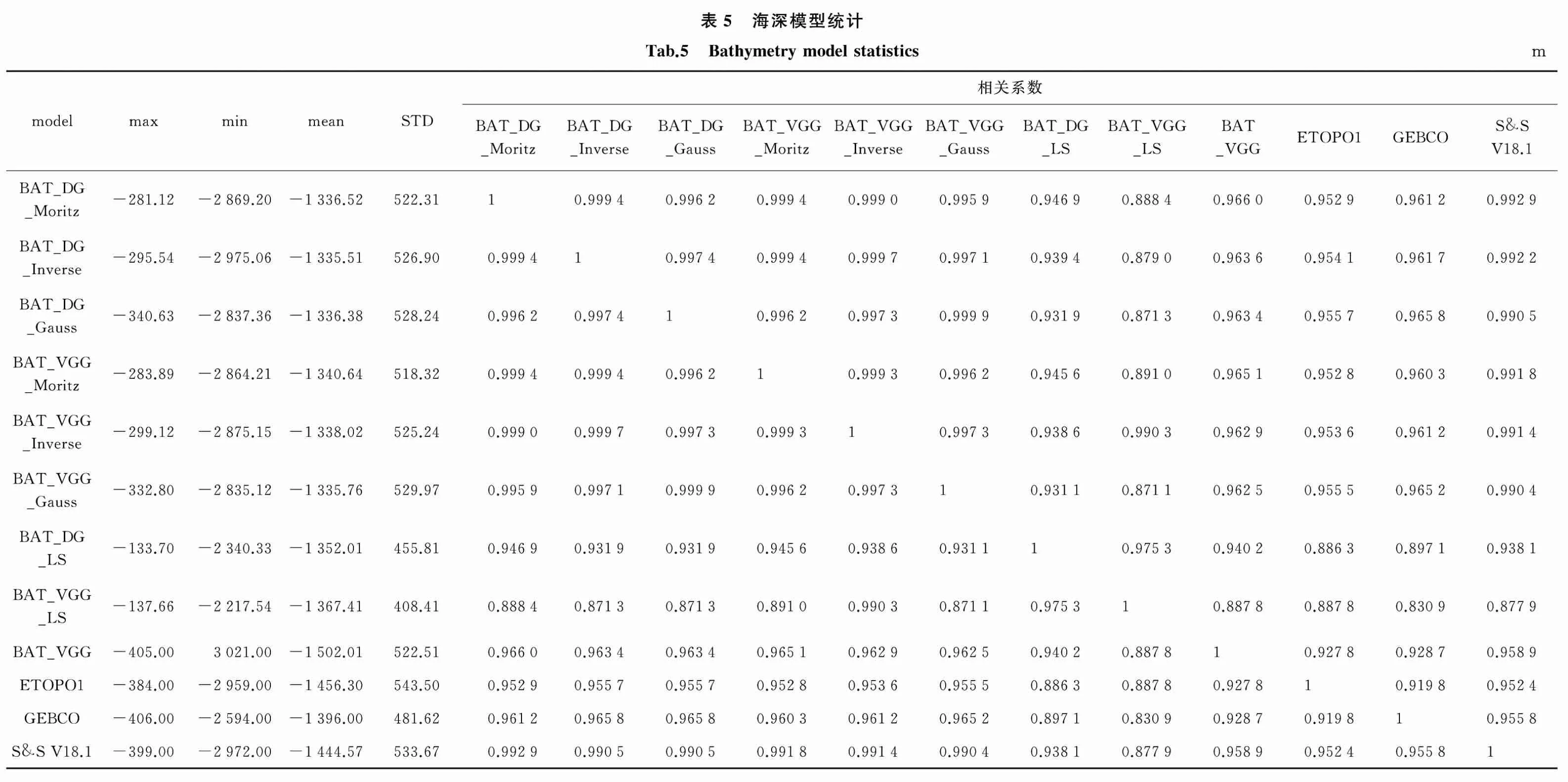
表6 海深模型检核统计结果Tab.6 Statistical checking results of bathymetry models

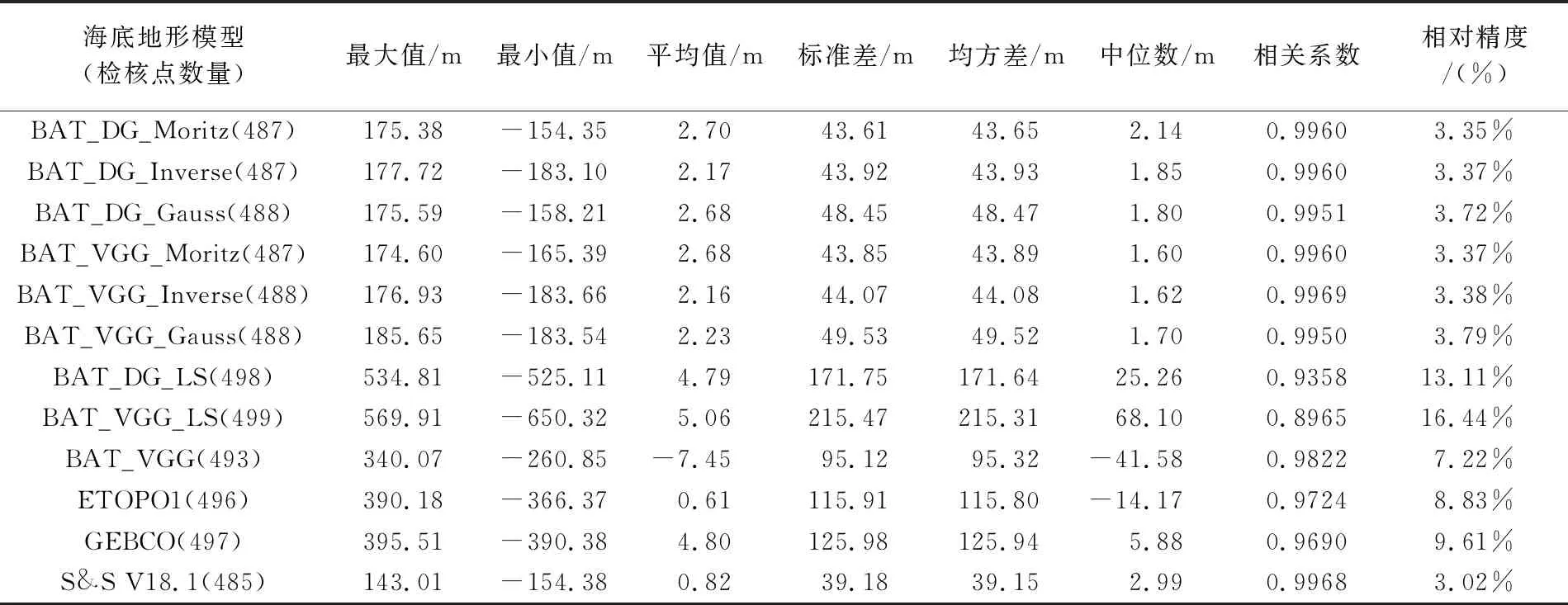
表7 海深模型扣除系统误差后检核统计结果Tab.7 Statistical checking results of bathymetry models after deducting system errors

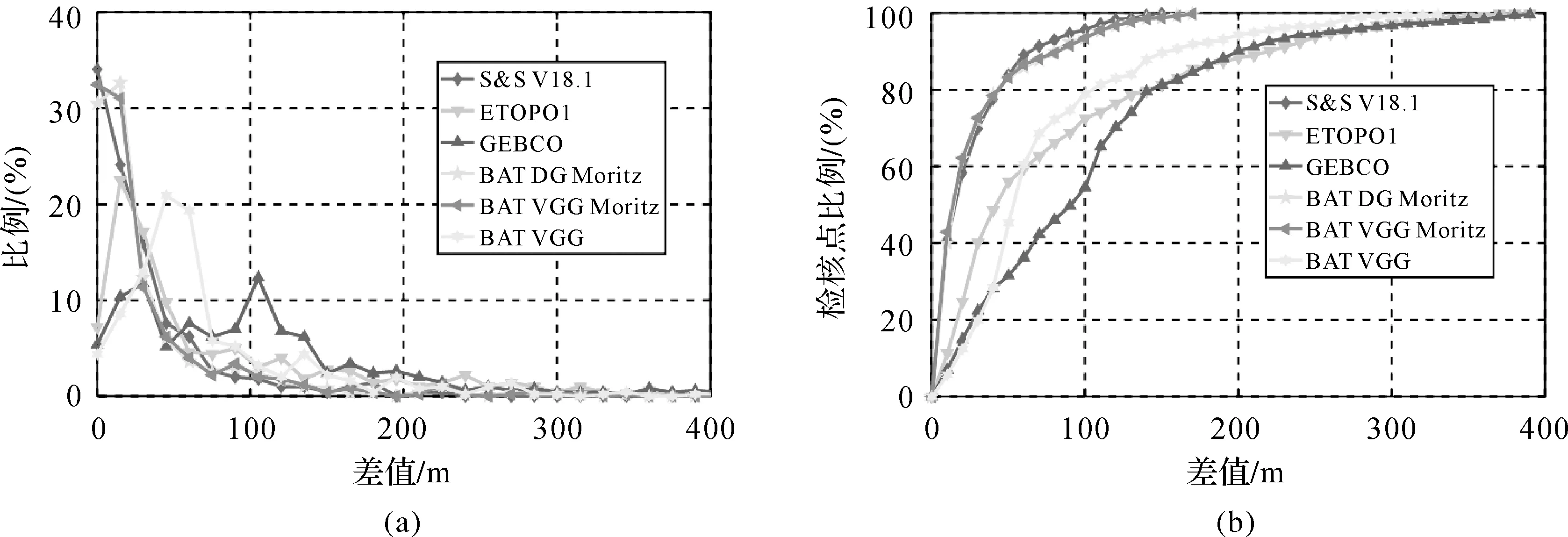
图10 不同差值范围检核点数量比例Fig.10 Ratio of checkpoints in different range of difference

导致各海深模型在目标海域表现产生差异的原因，笔者认为主要来自于两个方面。一是输入数据源、数据量和数据质量差异，如本文船测海深数据主要来源于NGDC发布的研究海域部分数据，ETOPO1模型数据来自于Japan Oceanographic Data Center (JODC)、NGDC和The Mediterranean Science Commission(CIESM)等组织，S&S V18.1模型船测数据包括NGDC、SRTM Topography、SIO Multibeam、NGA Digital Nautical Soundings、JAMSTEC Multibeam等；输入数据的丰富程度和数据质量优劣对最终海深模型质量影响明显。二是海深模型构建方法差异，BAT_VGG模型使用控制点地形和重力数据之比获取比例因子方法构建，而BAT_DG_Gauss模型和BAT_VGG_Moritz模型采用最小二乘配置方法建立，本文最小二乘配置方法实质上类似于回归分析拟合导纳系数，同时兼顾趋势项小的变化。SAS方法获取的比例因子是将控制点反演波段上地形和重力信息之比格网化，进而得到研究区域格网化的比例因子，采用该方法获取的比例因子不同格网点结果不同；而本文采用最小二乘配置方法解算的研究海域地形和重力数据比例因子是基于对全域控制点处地形和重力信息考察的结果，反映了整个区域海底地形和海面重力的趋势关系。从这一角度考虑，整个区域海底地形和海面重力的趋势关系与导纳函数反演海底地形方法类似。

分别沿研究区域南北和东西方向选择各选择一剖面位置，简要比较各海深模型表现状况，选择的剖面位置如图11(图11背景为S&S V18.1海深模型)中1号位置(#1)和2号位置(#2)所示。采用双线性插值方法作各海深模型在#1和#2的海深剖面图，海深剖面结果如图12所示。

图11 剖面位置Fig.11 Profile location

图12 剖面深度图Fig.12 Profile depth

海深剖面结果显示，#1由南到北海底依次出现了海山、山谷、平原等地貌形态，#2剖面地形呈现是东西两端为山地，两端之间为山谷地形。#1和#2海深剖面结果显示，BAT_DG_Moritz模型和BAT_VGG_Moritz模型地形走势几乎重合，二者相差很小；GEBCO模型相比其余模型地形走势更加“平滑”，反映海底地形细部特征能力较弱，比如在#1纬度为38.4°左右的海山位置和#2经度为134.2°附近范围的山谷位置，GEBCO模型反映地形能力有限；BAT_VGG模型在地形起伏区域，相比其他海深模型存在低估海山高度和高估山谷深度现象；ETOPO1模型在#1纬度为38.4°左右位置出现了与其余模型完全相反的地形呈现；BAT_DG_Moritz模型和BAT_VGG_Moritz模型在#1和#2均能较好反映对应位置的地形走势，从而从侧面说明了本文反演效果良好。

进一步描述和分析BAT_DG_Moritz模型和BAT_VGG_Moritz模型频谱特征，依据文献[41—43]可知，两格网输入数据的频率域相干性(Coherency)是以波长为自变量的线性相关系数的平方，表征输入数据间的线性相关程度。两格网信号相干性计算公式为

Coh=

(18)

式中，Coh表示相干性；M(fx,fy)和N(fx,fy)代表格网信号m(x,y)和n(x,y)的傅里叶变换；“*”号表示复共轭；〈〉表示方位角取平均(Cartesian坐标系转为极坐标系)。依据文献[44—45]计算功率谱密度(power spectrum density，PSD)方法获得不同波长对应的功率谱密度

PSD=10·lgP

(19)

式中，PSD单位是dB；P代表不同波长的能量。因S&S V18.1模型、ETOPO1模型、GEBCO模型和BAT_VGG模型构建过程中利用的数据源和数据量不同，从而主要对比BAT_DG_Moritz模型和BAT_VGG_Moritz模型频谱特征信息，PSD和相干性结果如图13所示。

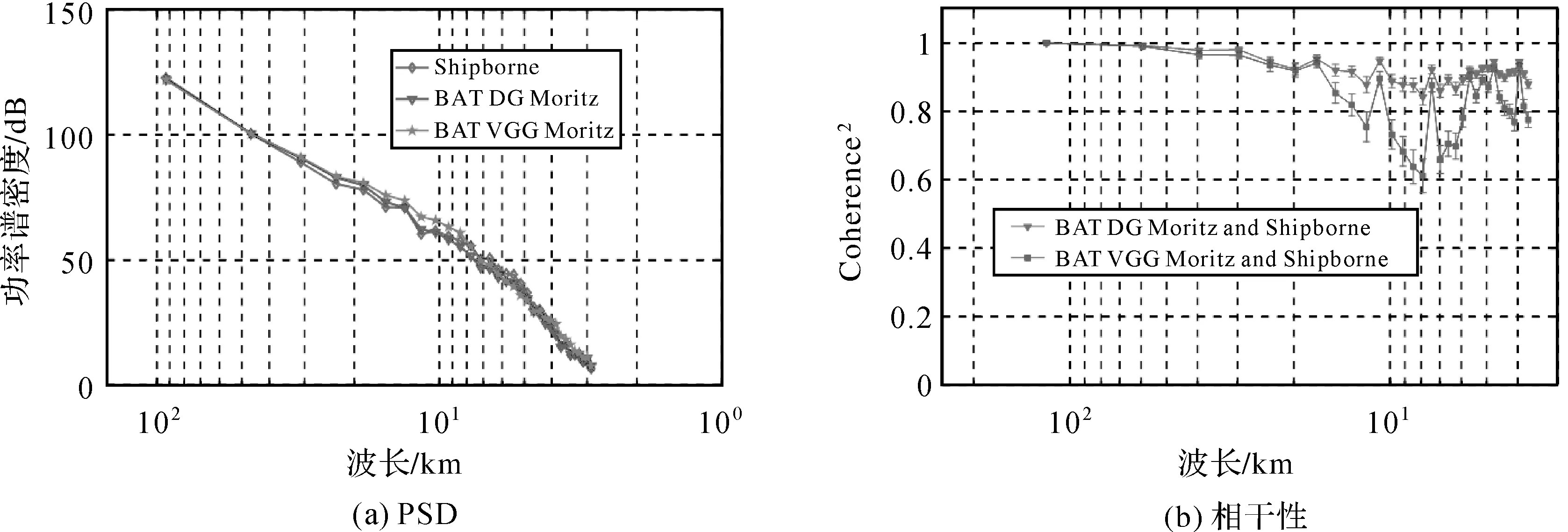
图13 PSD和相干性分析Fig.13 PSD and coherency analysis

图13中Shipborne为使用本文控制点数据，借鉴文献[45]格网化方法(Gridding with spline in tension)获取的格网化海深。利用式(19)计算的BAT_DG_Moritz模型、BAT_VGG_Moritz模型和Shipborne模型的功率谱密度折线如图13(a)中蓝色、绿色和红色所示。PSD曲线显示，BAT_DG_Moritz模型和BAT_VGG_Moritz模型可改善了Shipborne模型6 km波段以上信息，其中BAT_VGG_Moritz模型在高频部分改善更加明显。笔者在研究海区开展试算时，确定的带通滤波器波长初值为15 km，而PSD曲线显示最终反演海深模型却改善了Shipborne模型6 km以上波段信息。究其原因，笔者认为是由于试算过程中选择的滤波器本身机制所致。由于笔者使用带通滤波器滤波时，小于15 km波长的信息并非完全滤掉，而是存在部分保留信息，进而呈现出最终反演海深模型改善的波段范围大于初始选择频段现象。依据式(18)分别计算格网模型间的相干性，结果如图13(b)所示，其中红色折线表示BAT_DG_Moritz模型和Shipborne模型相干性结果，蓝色折线代表BAT_VGG_Moritz模型和Shipborne模型相干性结果。从图13(b)模型相干性结果可以看出，二者表现了较强的相干性(相干性结果均在0.5以上)，其中BAT_DG_Moritz模型和Shipborne模型相干性平均值分别为0.917 0。另外，BAT_DG_Moritz模型和BAT_VGG_Moritz模型相干性平均值达到了0.930 7。图13(b)相干性折线均呈现先减小后增大趋势，其中相干性减小波段是BAT_DG_Moritz模型和BAT_VGG_Moritz模型相对于Shipborne模型波段信息改善部分，其中重力异常垂直梯度反演海深结果与Shipborne模型相干性减小明显，再次验证了功率谱密度分析中关于BAT_VGG_Moritz模型在改善船测海深模型效能方面效果明显结论。由于本文试验在有限波段进行，因而对Shipborne模型短波和长波部分信息改善有限。

3 结 论

本文针对目前导纳函数方法、SAS方法和回归分析方法反演海底地形主要考虑海底地形和卫星测高重力数据线性趋势项而忽略非线性项影响现状，提出了采用最小二乘配置技术兼顾海底地形和重力数据线性项和与非线性项(与线性趋势项不符的小的变化)构建海底地形模型新的方法途径。然后，利用日本海某海域重力异常数据、重力异常垂直梯度数据和稀疏船测数据开展了方法试算验证工作，同时将本文反演结果与国际广泛使用的S&S V18.1和ETOPO1等海深模型进行了比对分析，可得到如下有益结论。

(1)相较于仅仅考虑海底地形和重力数据线性趋势项而建立的海深模型BAT_DG_LS和BAT_VGG_LS，本文采用最小二乘配置方法，利用相同重力数据获得的反演海深模型检核精度最低分别提高了大约2.5倍和3.5倍，以及相对精度最高分别提升了9.76%和13.07%，极大提升了海底地形建模质量。

(2)本文最小二乘配置反演模型与S&S V18.1、ETOPO1、GEBCO和BAT_VGG模型在研究海域相关系数均达到了0.95以上。海深模型检核差值和剖面海深分析结果表明：本文利用最小二乘配置方法构建的海深模型相对精度在3.8%范围内，各精度指标与S&S V18.1模型相当，远远优于ETOPO1和BAT_VGG等海深模型；GEBCO模型相比其余海深模型反映地形更加“平滑”，反映海底地形细部特征能力较弱，BAT_VGG模型在地形起伏区域，相比其他海深模型存在低估海山高度和高估山谷深度现象。

(3)海深模型相干性和功率谱密度特征分析表明：本文反演模型能有效改善研究海域船测海深相关波段信息(本文反演波段范围为15～160 km)，其中卫星测高重力异常垂直梯度相比重力异常为输入源建立的海深模型改善船测海深相关波段信息更为明显。

综上所述，本文采用最小二乘配置方法，兼顾海底地形线性趋势项和非线性项构建的海底地形模型表现良好，反演方法可行且有效。