课程思政元素融入高等数学的教学研究——以椭圆面积求解为例

王敏会 常桂娟

（青岛农业大学理学与信息科学学院 山东青岛 266109）

一、引言

2016年12月全国高校思想政治工作会议后，各高校纷纷开启课程思政建设。大学教师应充分利用好课堂教学这个渠道，立德树人，帮助学生建立正确的人生观、价值观和世界观，鼓励同学们向伟大的科研工作者学习，学习他们坚持真理的科学态度。作为高校教师，不仅要有扎实的专业知识，还要有深厚的思想政治理论知识，将思政元素与课堂授课有效融合，培养全面发展的综合性创新人才。

二、解题方法探索

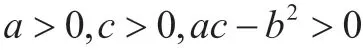
求平面图形面积常用的方法有定积分、二重积分、第二型曲线积分，对于一些特殊曲线围成的面积，除了上述三种方法外，我们还可以根据图形的特点，巧妙地采用其他方法来求它的面积。对于本文中的题目，除应用积分的方法外，还通过运用坐标轴旋转、拉格朗日乘数法以及变量替换，求出了它的面积。

解法一（坐标轴旋转[1]）

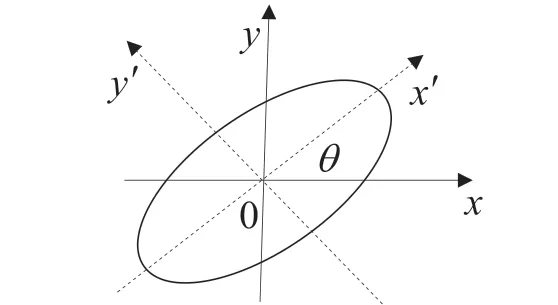
图1 坐标轴旋转

以上给出了中心在坐标原点，对称轴不在坐标轴的椭圆的面积的六种求法，对于中心不在原点的椭圆，为求其面积，可以先通过坐标轴平移的方法，将坐标原点平移到椭圆的中心，再根据本文给出的结论，即可求出更常规椭圆的面积。