以学掌舵,驶向思维纵深处

王志平

摘要：《新课程标准》非常重视培养学生的学习能力，新的教学理念打破了常规课堂教学模式，让学生真正成为课堂的主人，积极参与课堂教学环节。本文以“备学”“互学”“问学”“研学”“展学”为途径，阐述了为学生精心准备学习素材，让学生自我研究和自我展示的方法。

关键词：备学  互学  问学  研学  展学  思维纵深处

中国有句古语：“授之以鱼，不如授之以渔。”课堂教学知识主要来源于课本，因此教师要鼓励学生自主探究，积累学习能力，获取知识，丰富自己的知识体系，教师要注重培养学生学习知识的能力。

一、“备学”启航，巧设素材

皮亚杰用很多实验证明：儿童学习一定要做好充分的准备。教师要精心为学生准备一系列需要课堂探究的学习素材，感悟学习新知。课堂教学前，教师要精心“备学”，为学生精心准备学习素材，以便达到更好的教学效果。教师要及时了解学生思维闪光的细节，才能真正激发学生学习的内在动力，打造精彩课堂。

如在教学“商的变化规律”时，笔者先让学生完成两张表格，如表1、表2所示。在完成表格前四列后，学生已初步感悟了商的一些变化规律，再根据前四列的规律自主创造第五列，最后教师让学生根据自己的理解说说商变化的规律。基于学生已有学习经验，利用教学素材，自主感知商的变化规律，总结商的变化规律。

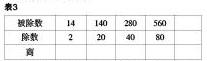
在学生掌握了商的变化规律后，教师可引导学生探究，商除了变化规律，还有什么规律。教师出示第三张表格，如表3所示。

首先，教师要让学生先独立填写表格前四列的内容，然后让学生通过小组的形式进行讨论：“你发现了什么？”学生通过讨论得到了雏形的商不变性质，即被除数和除数同时扩大或缩小相同的倍数，商不变。这时，有的学生说：“如果在最后一栏被除数和除数同时乘0，都变成0的话，这个结论好像就不成立了。”接着，教师可以继续追问：“为什么觉得填上0就不成立呢？……看来这个相同的数不能为0，你觉得刚才的发现该怎么补充？”学生讨论后，得出结论：在除法中，被除数和除数同时乘或除以一个相同的数（0除外），商不变。

因此在“备学”时，教师需要多空出一列，让学生填写。有些学生会依照前几列填写，而有个别学生会创造出其他的填写方法，这正是教师所需要的创新。

二、“互学”互助，对话点拨

同学只有与同学不断切磋、不断挑战，才能激活自身思维。“互学”指的是把想法毫无保留地分享给同学，并清晰地阐述自己的见解，达到共同提高。学生在课堂上众说纷纭，面对有疑惑的学生，教师应集众人之力给予学生帮助。

如在教完工程问题后，有这样一道习题：“工地需要运来1200吨沙子，一辆卡车5天运了这堆沙子的   。照这样计算，这堆沙子还要运多少天？”学生学习了工程问题和分数解决问题后，创造出了许多意想不到的解题方法：

方法1：1200÷（1200×   ÷5）-5=15（天）

方法2：（1200-1200×  ）÷（1200×  ÷5）=15（天）

方法3：1200×（1-   ）]÷（1200×   ÷5）=15（天）

这时，突然有学生说：“我有一种方法，算式特别简单，5÷    -5=15（天）。”

把这堆沙子看作单位“1”，5÷   ，表示全部运完要多少天，再减5，就是还要运多少天。这时，全班学生脑洞大开，创造出了方法5、方法6、方法7。

方法5：1÷（   ÷5）-5=15（天）

方法6：（1-    ）÷（    ÷5）=15（天）

方法7：5÷   ×（1-    ）=15（天）

在前3种方法中，学生把1200吨沙子看作单位“1”。当出现5÷    -5=15（天）时，学生顿时打开了思维的闸门，创造出了方法5、方法6、方法7。这样一来，想出某种解题方法的学生就可以先清晰阐述解题思路，假如该学生无法清晰阐述，其他学生可以补充或者教师可以加入进行点拨。通过“互学”，教师可以适当点拨，让学生主动创造发挥，得到更多解题方法。

三、“问学”促思，质疑求新

“问学”促思可以启发学生求异思维，促进学生深度理解。在小学数学课堂教学中，很多教师依然停留在“怎么教”的阶段，对于“教什么”缺乏深入理解。教师可以通过追问发展学生的异向思维，使学生深入理解教学内容。而“问学”恰恰要问到关键，引领学生创新思维。

如在教学“长方形和正方形的周长”后，教师可出示这样一道题目：“有一张长25厘米，宽15厘米的长方形，从中剪去一个最大的正方形，剩余部分周长是多少厘米？”学生可以根据题意画图，先找到长方形的长和宽，再计算长方形的周长，这种定势思维很容易让学生的思考模式化，陷入僵局，不利于发展学生的发散思维。从深度发展学生数学思维的角度出发，教师可以追问：“还有更简单的方法吗？”学生陷入沉默，突然有位学生站出来，说：“剩下长方形的周长比原来短2个‘宽。”学生结合图形，利用线段旋转平移，发现剩余图形的周长与原来长方形的宽无关，而是原来图形长的2倍，如图1所示。

这样的“问学”启发了学生在“异”中推进思考，不仅可以让学生完成基本知识的学习，还在求异思考中渗透了转化思想，深度推进学生思路，加深了学生对数量关系本质的理解。学生逐步学会“自问”，对解决问题产生了求异和创新思维。

四、“研學”探究，突破关键

“研学”指的是学生针对一些抽象的数学问题，自己研究创造附加一些条件，从而解决问题。数学知识本身就抽象，教学时教师需要主动搭建一系列知识台阶，让学生不停研究学习，产生思维火花，突破学习难点。

如在教学百分数时，有这样一道例题：“某种商品六月价格比五月下降20%，五月价格比四月增长20%，那么六月价格和四月相比，是涨价了还是降价了？变化幅度是多少？”这题没有具体的量，学生束手无策。教师帮助学生研究题目的具体条件：六月价格比五月下降20%，把五月价格看作单位“1”;五月价格又比四月涨了20%，又是把四月价格看作单位“1”。那最后研究把哪个月的价格看作单位“1”，完成题目更方便？学生回答：“四月。”然而，这里的四月没有告诉学生价格是多少，因此可以假设一个具体量来解题，对此，学生以小组为单位，四人合作进行研究。

教师出示学习单：假设四月价格是（     ）元，那么五月价格是（      ）元，六月价格是（      ）元。

学生进行列式解答，通过小组研究学习后，反馈时有各种情况如下：第一，假设四月价格是100元，100×（1+20%）×（1-20%）=96元，（100-96）÷100=4%;第二，假设四月价格是10元，10×（1+20%）×（1-20%）=9.6元，（10-9.6）÷10=4%;第三，假設四月价格是1元，1×（1+20%）×（1-20%）=0.96元，（1-0.96）÷1=4%。

教师分别展示学生小组学习的成果，这时，有学生回答：“可以把四月假设成具体数量，直接把它看作单位‘1，1×（1+20%）×（1-20%）=96%，  1-96%=4%。”这样一来，貌似很复杂的例题，通过教师的适当点拨，学生就可以展开假设，讨论解题方案，把四月产量看作单位“1”的最佳解题策略。

五、“展学”交道，感悟升华

“展学”是学生在完成新知识的学习后，在练习中展示自己运用知识解决问题的本领。学生之间互相介绍学习成果，遇到思维碰撞，获取知识，使认知得到升华。

在教学乘法分配律后，笔者给学生出示了一道选择题：“以下四个算式中，得数最大的是哪个？①1994×1999+1999;②1995×1998+1998;③1996×1997+1997;④1997×1996+1996。”经过讨论后，大部分学生通过计算结果来比较乘数大小，只有个别学生觉得计算太麻烦，认为一定会含有某种隐藏的简便方法。这时，教师可引导学生仔细观察：“这四个算式在形式上完全相同，用乘法分配律把原算式进行变式：①1995×1999;②1996×1998;③1997×1997;④1998×1996。”面对选择得数最大项的问题时，学生联系长方形的周长和面积关系可以发现：“长方形的周长相等，长和宽越接近，面积越大，直到长和宽相等，变成正方形时，面积最大。”学生把长方形的相关知识迁移到题目中，猜测两数之和相等，相差越小则积越大。学生运用数形结合，得出和相等的两个数，相差越小则积越大。因此，答案应选③1996×1997+1997。

课堂是学生的课堂，学生是课堂学习真正的主人，学会学习是学生的终极目标。越来越多的教师有意识地让学生互动交流，自主学习模式渐渐成为主流，使学生真正成为课堂学习的掌舵人，使学习之舟驶向思维的纵深处。

参考文献：

[1]徐颖.数学题特殊性思考[J].中小学数学，2018（3）.

[2]杨念庆.浅谈课堂教学中的有效提问[J].天津教育，2010（4）.

[3]钱学锋.沟通内在联系，完善知识结构[J].小学教学设计，2018（5）.

[4]黄海燕.让一切回到原点[J].小学教学研究，2018（1）.

（作者单位：浙江省玉环市陈屿中心小学）