堆积床相变储热系统中径向孔隙率振荡分布对热性能的影响
2021-08-13刘红兵赵长颖
刘红兵,赵长颖
© 2021 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
1. 综述
太阳能由于具有清洁、安全和取之不尽、用之不竭的巨大优势而得到了越来越广泛的应用[1,2]。根据REN21的报告,聚光太阳能发电(CSP)设施和太阳能光伏发电设施(PV)的总装机容量从2018年的512 GW增长至2019年的627 GW,占可再生能源增长总量的60.21% [3]。然而,太阳能具有间歇性和波动性,需要储能技术来解决其固有缺陷并提高能量存储和利用效率。在太阳能的热利用方面,相变储热拥有更高的储能密度并在相变过程中保持几乎恒定的温度,该特性引起了广泛的关注[4,5]。相变储热的主要限制因素是相变材料较低的导热系数(0.2~0.8 W·m-1·K-1),因此需要采取有效措施提升其传热速率[6]。与壳管式单元相比,对于相变蓄热单元,堆积床是一种更加高效的热能存储方式。据Li等[7]研究,堆积床相变储热系统的储热速率是管壳式储热系统的1.8~3.2倍。
在堆积床相变储热系统中,由于换热流体直接流过相变胶囊,因此相变胶囊的分布情况会极大地影响流场的分布[8,9]。对于球形堆积,最密堆积方式为面心立方堆积和六方最密堆积,其堆积密度达到74.05% [10]。但是,当球体随机分布在容器中时,由于壁面的缘故,球体无法达到最密排列结构,这种现象称为壁面效应[11]。Mueller [12]的研究表明,堆积床内部孔隙率沿着径向方向呈振荡分布。此外,径向孔隙的振荡分布会导致流场不均匀,这将进一步影响堆积床内部的传热效果[13]。由于容器为圆柱形,壁面对胶囊的平均填充密度的影响随着容器和球体的直径比(D/dp)的减小而显著增加[14]。当使用堆积床进行相变储热时,如果想要达到较高的储热能力则要求系统具有较小的储罐尺寸和直径比。因此,在堆积床相变储热系统的数值研究中应考虑径向孔隙率的变化,特别是对于小直径比(D/dp<10)的情况 [15]。
针对堆积床相变储热的计算模型,根据是否需要描述具体的堆积结构,可以将模型分为两类:基于表征体元尺度(REV)的模型和基于孔隙尺度的模型。在基于表征体元尺度的模型中,主要通过控制方程计算换热流体与相变材料的热物性变化。Benmansour等[16]采用双方程模型来表示换热流体与相变材料的能量方程,而方程中采用的孔隙率是一个常数。因此,该研究没有考虑径向孔隙率的变化[17]。随后的研究中,他们用一个指数表达式替代了能量方程中属于常数项的孔隙率。在该表达式中,径向孔隙率φ(r)是与壁面相隔距离的函数[18,19]。此外,为了计算相变胶囊内部的温度梯度,有研究提出了Dispersion-concentric (DC)模型。Karthikeyan和Velraj [20]比较了双方程模型和DC模型;其结果表明,考虑到相变胶囊内部的内部传热,DC模型的结果与实验结果更加吻合。但是,其所采用的数值方法是REV方法,而小直径比(D/dp<10)的堆积床不能视为连续的多孔介质。由于网格无法精确描述孔隙和实体骨架,因此无法满足REV尺度模型的要求[21,22]。
在孔隙尺度模型中,基于对相变胶囊的具体分布的描述,可以计算出换热流体的流量以及换热流体和相变胶囊之间的传热量。Xia等[23]开发了一种高效的堆积床模型,将三维堆积床转化为二维堆积床。相应的转化标准是确保两个堆积床具有相同的孔隙率。但是,在转换过程中该模型未考虑径向孔隙率的分布。此外,该模型中的相变胶囊并不相互接触,并且忽略了胶囊之间的热传导。由于转化过程中相变胶囊之间的流道发生了变化,因此其流场与真实流场有差异。
综上所述,本文根据球体的实际堆积过程,构建了考虑径向孔隙率的振荡的三维堆积床相变储热模型,揭示了径向孔隙率振荡分布的原因,探究了径向孔隙率的分布对换热流体的径向相对速度分布以及相变材料的温度分布和液相分数分布的影响,并进一步讨论了无量纲参数直径比、雷诺数、史蒂芬数对堆积床相变储热单元内径向流动传热特性的影响。
2. 三维堆积床相变储热模型的建立
2.1. 物理模型的建立
在研究三维堆积床时,面临的主要困难是建立有效的球体填充模型。球体堆积过程中,小球之间存在碰撞和摩擦作用,因此需要计算小球在重力、摩擦力以及相互作用力的作用下的运动轨迹,最终确定稳定状态下所有小球的位置。建立堆积床的现有方法包括DEM方法[8,24,25]、Blender法[26,27]和蒙特卡洛法[15,28]。在本研究中,采用开源软件Blender建立了三维堆积床模型。Blender软件搭载了Bullet Physics Library,可以有效地计算小球在重力作用下的物理过程。在建模过程中,首先建立了一个圆柱形容器。然后,不断在容器上方随机产生小球,使其掉落,如图1(a)所示。在堆积过程中计算每个球的位置。如果所有球的位置都达到稳定状态,则可以认为堆积过程达到了稳定状态。
孔隙率是空隙体积与总体积的比率,而表面孔隙率是空隙面积与表面总面积的比率,如等式(1)~(3)所示[29]。在这项研究中讨论的径向孔隙率是表面孔隙率。为了计算径向孔隙率,沿径向方向截取了一系列圆柱表面。对于每个圆柱表面,采用射线投射算法来确定球体内部区域。然后将所有球体内部面积相加,并用球体的总面积除以圆柱表面的面积,如图1(b)所示。
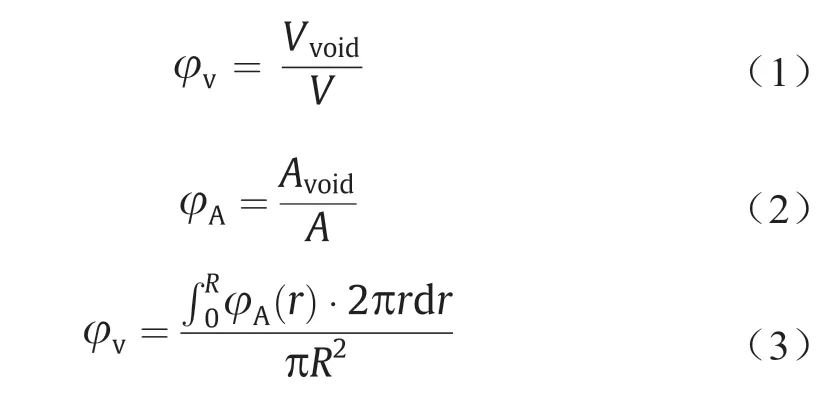
在图2中,在Blender中建立了直径比为7.99的模型,将径向孔隙率与Mueller的结果进行了比较[12]。由图2可知,两条曲线均呈振荡分布且吻合较好,从而验证了模型的可靠性。此外,径向孔隙率的振荡分布表明堆积床不能处理成均匀多孔介质,这也进一步证明了建立三维模型的必要性。
在堆积床中,球之间的接触类型为点接触,这不利于网格的生成。当前有四种方法处理接触点问题:重叠法、间隙法、压平法和桥梁法。在具有热传导的情况下,桥梁法可以达到最佳效果[30]。因此,直径为dp/10的小圆柱体作为热桥被插入到每两个接触的球体之间,这会导致堆积床的平均孔隙度变化0.05%~0.08%。此外,球体与壁面接触点的处理采用了间隙法,在球体和容器壁之间形成一个1 mm的间隙。
如图3所示,本文建立了三维堆积床相变储热模型。在该模型中,将205个相变胶囊装入一个内径为240 mm的圆柱形罐中,其中相变胶囊的直径为48 mm;计算得到堆积床的直径比为5。选择三元碳酸盐Li2CO3-K2CO3-Na2CO3(32 wt%-35 wt%-33 wt%)作为相变材料,其热物性如表1所示。堆积床被放置在中间部分,同时在入口和出口的两侧添加延伸部分以消除进出口段的影响。

表1 三元碳酸盐相变材料热物性
2.2. 数学模型
2.2.1. 模型假设
(1)忽略重力对换热流体的影响;
(2)忽略相变胶囊中相变材料的对流作用;
(3)忽略换热流体与相变胶囊的辐射传热。
2.2.2. 换热流体的控制方程
在堆积床相变储热系统中,基于相变胶囊直径的雷诺数定义为[9]:

图1. (a)球的堆积过程;(b)沿径向生成次表面的示意图。

式中,ρ是密度;μ是黏度;uin是入口速度。
由于堆积床内流道复杂,内部流动通常为湍流。考虑到相变胶囊的换热表面为球面,并且为了增强对壁面的处理,换热流体的流动使用RNGk-ε湍流模型进行计算。因此堆积床相变储热系统的控制方程在直角坐标系下可以写成如下形式[31]。
连续性方程:

动量方程:
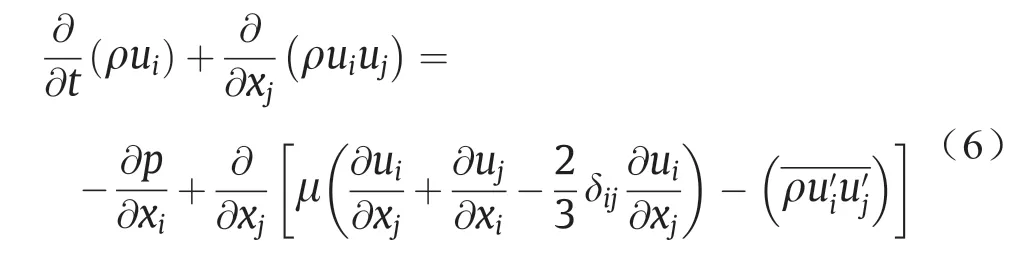
能量方程:

k方程:

ε方程:
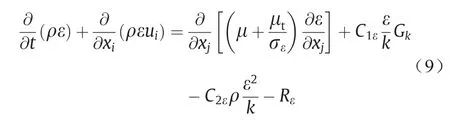
式中,xi和xj分别是在i和j方向上的距离;ui和uj分别是换热流体在i和j方向上的速度分别是换热流体在i和j方向上的波动速度;E是能量;(τij)eff是有效的雷诺张量;k是湍流动能;ε是湍流耗散率;σT是能量方程式中的普朗特数;σk是湍流动能方程中的普朗特数;σε是湍流耗散率方程式中的普朗特数;C1ε和C2ε是两个模型常数。湍流黏度μt、湍流动能的产生项Gk以及附加项Rε由下式给出[32]:

图2. 直径比为7.99时径向孔隙率分布的比较。
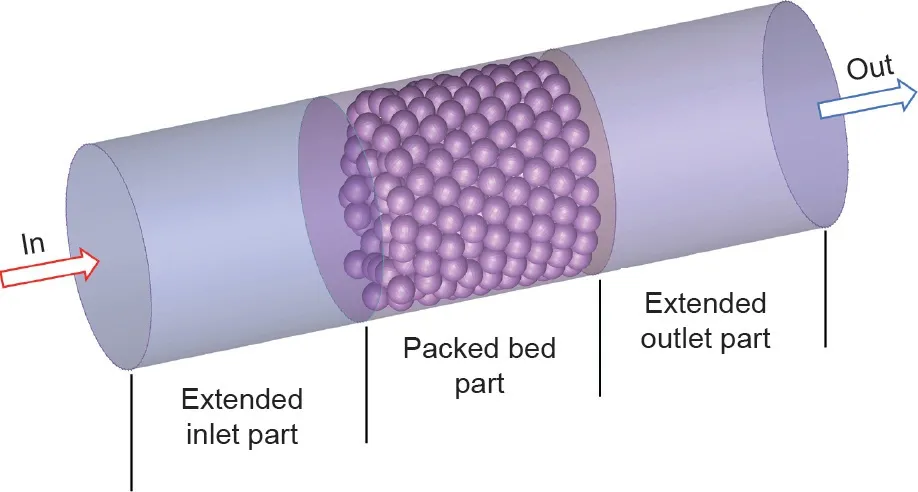
图3. 三维堆积床相变储热系统模型示意图。
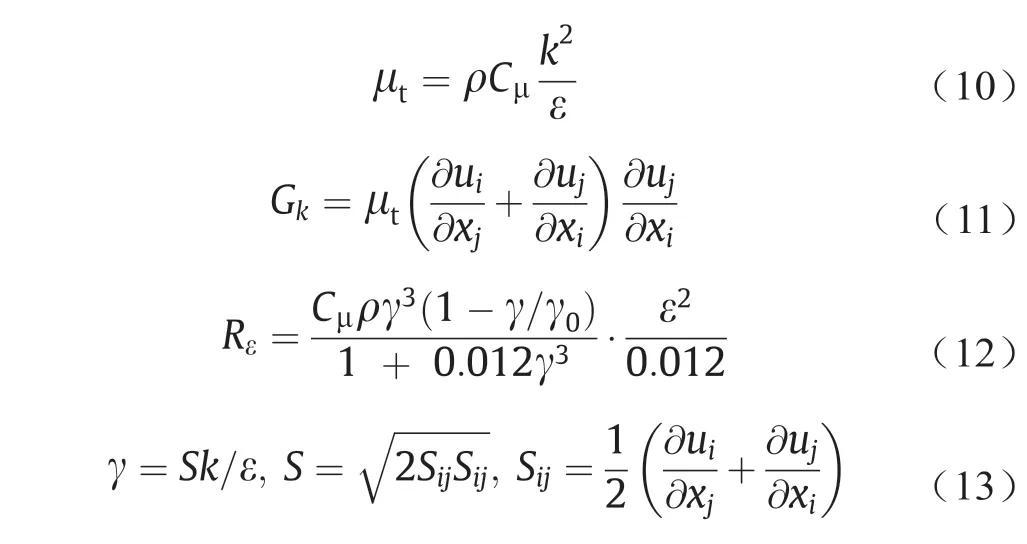
式中,Cμ是模型常数;γ是RNGk-ε湍流模型系数;γ0是初始状态下的RNGk-ε湍流模型系数;S是流体的平均应变率;Sij是变形张量。
上述方程式中的常数为:σT= 1.0,σk=σε= 0.72,Cμ
2.2.3. 相变材料的控制方程
相变胶囊中相变材料的自然对流作用较弱,故而忽略,因此能量方程可以表示为[23]:
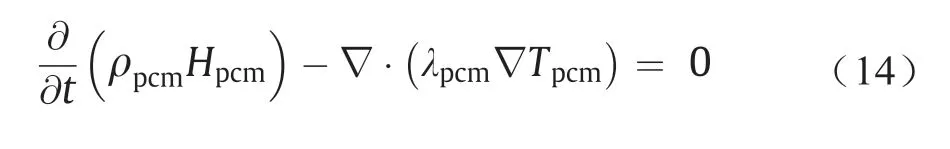
式中,Hpcm代表相变材料的焓值,定义为显热和潜热之和;∇是梯度算子。
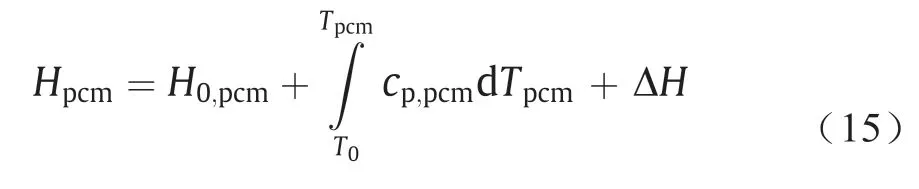
式中,H0,pcm代表相变材料在初始温度下的焓值;△H代表相变材料储热过程中释放的相变潜热,定义为ΔH=βL,L代表相变材料的潜热值,β代表相变材料的液相分数,β在不同的温区下表示为:
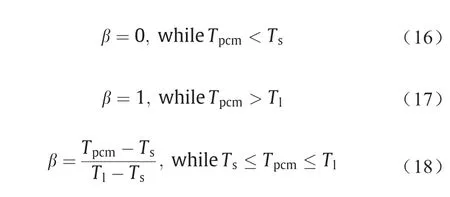
式中,Tpcm,T0,Ts,Tl分别代表相变材料的温度、初始温度、开始熔化温度和终止熔化温度。
另外,储热过程中相变材料的史蒂芬数定义为显热量与潜热量的比值[33]:

式中,Tin是指入口换热流体的温度。
2.2.4. 边界条件与初始条件
储热过程开始前,堆积床相变储热系统保持在初始温度且有Tf=Tpcm=T0。储热开始时,入口处的换热流体以恒定的温度Tin和质量流量qin进入系统中,设出口处换热流体在垂直于出口方向的热流为零。因此,堆积床相变储热系统中边界条件如下。
进口处:
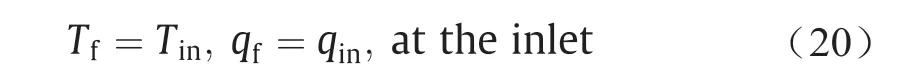
出口处:

式中,z是高度。
同时为了后续更好地分析径向孔隙率对换热流体径向特性的影响,储热罐的壁面设置为绝热边界条件:

2.3. 堆积床相变储热系统的储热
堆积床相变储热系统的总储热量包括相变材料、相变胶囊壳体以及储热罐壁面存储的热量。其中,相变材料储热量包括固态显热、液态显热和相变潜热,而相变胶囊壳体以及储热罐壁面存储的热量均为显热。系统的储热时间定义为靠近出口处相变胶囊温度达到低于入口温度1 K所用的时间。因此,堆积床相变储热系统的总储热量Qtotal可以表示为:

式中,Qpcm、Qshell和Qtank分别是相变材料、相变材料胶囊壳和储罐中的热量存储;mpcm、mshell和mtank分别是相变材料的质量、相变材料胶囊的外壳和储罐的质量;Cp,s和Cp,l是固态和液态相变材料的比热容;Tm、T0和Tin分别是熔化温度、初始温度和入口温度;Cp,shell和Cp,tank分别是外壳和储罐的热容量。
在储热过程中,堆积床相变储热系统的实际储热量Qstored可以通过热力学第一定律计算得到:
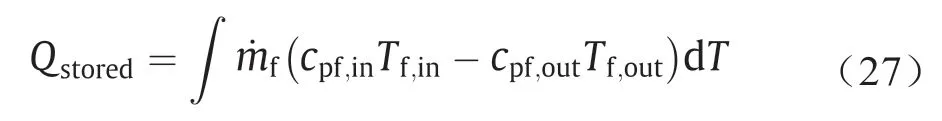
式中,mf是换热流体的质量流速;Cpf,in和Cpf,out分别是换热流体在入口和出口的比热容;Tf,in和Tf,out分别是入口和出口处换热流体的温度。
储热过程中的平均储热功率为[7]:

式中,τcharge是储热时间。
2.4. 数值计算方法
由于有数百个相变胶囊随机填充在堆积床中,因此采用非结构化网格对该三维结构进行网格划分。首先利用shrink-wrap方法对堆积床球体表面进行包面处理,然后使用多面体网格进行网格的填充[34]。随后,确定网格尺寸对填充时间和堆积床中压降的影响,并选择dp/18网格尺寸进行网格生成,如图4所示。在计算过程中,利用SIMPLE算法实现压力场与速度场的耦合迭代,离散方程采用二阶迎风格式,瞬态方程的求解则是使用了二阶隐式格式。
Li等[7]搭建了堆积床相变储热实验系统,该系统由385个相变胶囊随机堆积而成。系统中储热罐内径为260 mm,相变胶囊外径为34 mm,所以储热罐与相变胶囊的直径比为7.65。相变胶囊中的相变材料选取三元碳酸盐 Li2CO3-K2CO3-Na2CO3(32 wt%-35 wt%-33 wt%),其热物性如表1所示。该系统测试了三个不同高度方向上相变胶囊内部相变材料在储热过程中的温度变化,同时可以验证本文建立的三维堆积床相变储热系统模型。如图5(a)所示,相变胶囊沿高度的位置为z/H= 0.25、0.5、0.75。在装料过程中,质量流量qin为260 kg·h-1,而堆积床的初始温度T0为325 ℃,换热流体的入口温度Tin为465 ℃。
如图5(b)所示,三个位置处的模拟数据与实验数据均吻合较好,其中z/H= 0.5处的结果最佳。储热过程刚开始时,模拟数据快于实验数据;但是相变材料完成相变过程后,模拟数据与实验数据基本同步,并且模拟与实验几乎同时完成储热过程。一方面,将换热流体从初始温度(如325 ℃)加热到入口温度(如465 ℃)的加热过程较长,而在模拟中这一过程是在很短时间内完成的。另一方面,当储热过程进行到液态储热阶段时,相变材料已经完成了相变储热过程,初始状态下入口温度变化的不同而造成的储热量的差异相对于系统整体的储热量而言已经很小,所以模拟数据与实验数据越往后吻合度越高。总体而言,模拟与实验结果的对比验证了三维堆积床相变储热模型的可靠性与有效性。
3. 结果与讨论
3.1. 流动性能与热性能分析
本节中,堆积床的初始温度T0为325 ℃,直径比为5,HTF的入口温度为465 ℃,质量流量为260 kg·h-1。因为堆积床的平均孔隙率为0.437,计算得到相应的雷诺数Rep为4998.72,可认为堆积床内的流动为湍流。
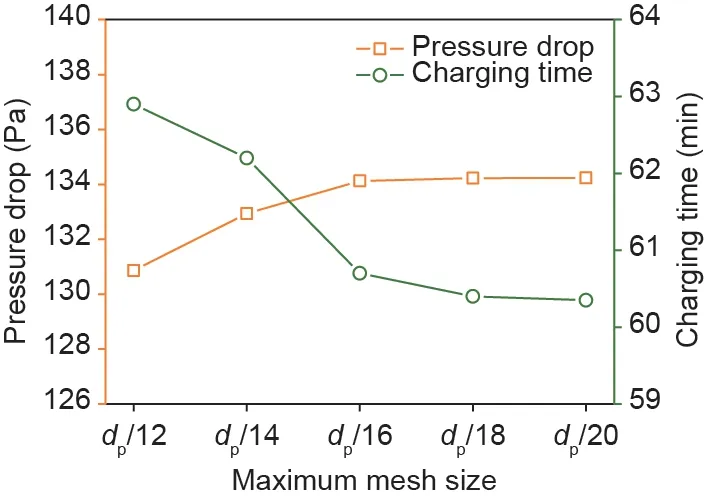
图4. 网格无关性验证。
3.1.1. 径向孔隙率振荡分布的原因
对于直径比为5的堆积床相变储热单元,其径向孔隙率分布如图6所示。为了更直观地说明,截取了堆积床内部不同径向位置的圆柱面,这些圆柱截面距离储热罐壁面的距离分别为0、0.25dp、0.5dp、0.75dp、dp、1.25dp、1.5dp、1.75dp、2dp和2.25dp。圆柱截面上蓝色区域代表换热流体,白色区域则为相变材料。根据面孔隙率的定义可知,距离壁面0、dp和2dp的圆柱截面孔隙率高于其他截面的孔隙率,而这与相变胶囊的堆积过程以及胶囊的形状有关。在堆积过程中,相变胶囊往往倾向于先填充靠近墙壁的空间,然后再填充储热罐中心的区域[35]。由于相变胶囊的外壳是球形,所以壁面处相变胶囊与储热罐壁面只有点接触,该位置的孔隙率则接近1,这也意味着圆柱截面上几乎全是换热流体区域。在距离壁面0.5dp处,圆柱截面刚好穿过相变胶囊的中心,这意味着相变材料区域将占据圆柱截面的大部分区域,从而导致孔隙率降低到了0.15。同样地,在距离壁面dp的圆柱截面上,靠近壁面的相变胶囊与内部相变胶囊的接触方式也是点接触,所以在接触位置附近能够形成较大的间隙,导致孔隙率增大至0.67。因此,径向圆柱截面上的孔隙率表现为高低交错的分布,即径向孔隙率呈振荡分布。
3.1.2. 流速分布
类似于堆积床中径向孔隙率的定义,径向流速为不同径向位置圆柱截面上换热流体的平均流速,定义为:
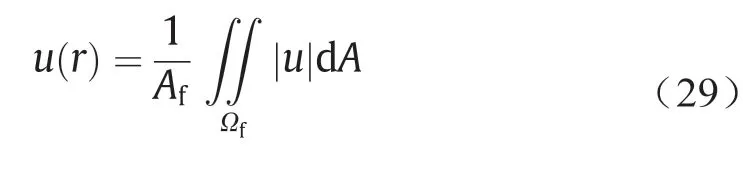
式中,Ωf代表圆柱截面上换热流体的区域;Af代表圆柱截面上换热流体区域的面积。
相对流速U定义为径向流速u(r)与入口流速uin之比:

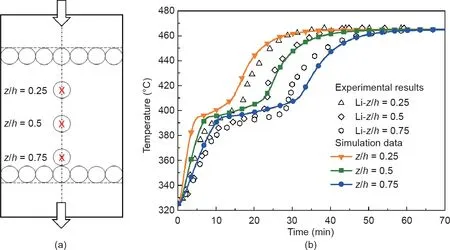
图5. (a)热电偶布置示意图;(b)模拟结果与实验数据对比。

图6. 径向孔隙率分布及径向圆柱截面示意图。

图7. 径向方向相对速度分布。
图7展示了堆积床内换热流体相对速度沿径向方向的分布,可以发现相对速度也呈现出振荡的分布。尽管堆积床在壁面处的孔隙率接近1,但由于换热流体与壁面之间存在黏性作用,壁面处的流速为0。沿着远离壁面的方向,换热流体的流速急剧增大并呈现出与径向孔隙率一致的分布。换热流体进入堆积床后从相变胶囊之间的空隙流过,空隙越大的径向位置对换热流体的阻力就越小。所以孔隙率大的位置有更多的换热流体流过,相应的流速也更大。为了便于对相对流速分布进行分析与比较,我们将堆积床沿径向方向分为两个区域:近壁面区域和中心区域。其中近壁面区域为从壁面到远离壁面0.5dp的区域,流速在这里发生了剧烈的变化;而中心区域则是从远离壁面0.5dp到罐体中心的区域,流速在这里的变化则更为平缓。
近壁面区域流速变化剧烈,所以评判该区域最重要的参数便是壁面附近的最大相对速度。在本算例中,壁面附近最大的相对速度为3.49。根据连续性方程可知,在相同的流量下,流速的变化与流道面积变化成反比[见式(31)]。因此当流体在堆积床中流动时,如果流道突然收缩,流速会相应地增大。图8展示了堆积床中不同位置截面上的流速分布。能够明显观察到,壁面附近换热流体的流速在经历流道收缩时大幅增大,这也就是壁面附近流速变化剧烈的原因。

图8. 堆积床内流速分布。

中心区域换热流体的相对流速呈现出更加平缓的分布,和径向孔隙率的分布一致。为了衡量换热流体流速的不均匀性,我们提出使用相对流速的标准差进行评估,如式(32)所示。标准差越大意味着径向位置上流速的分布差异越大,即流速的分布越不均匀。对于该直径比为5的堆积床,当雷诺数Rep为4998.72时,相对流速的标准差为0.39。
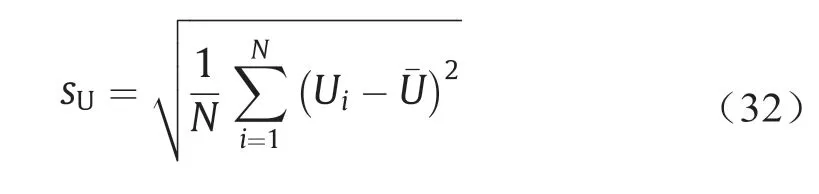
式中,N为截面的个数;ui为第i个截面的相对速度;u为所有截面相对流速的平均值。
3.1.3. 径向温度和液相分数分布
相变材料的径向温度和径向液相分数分别定义如下:
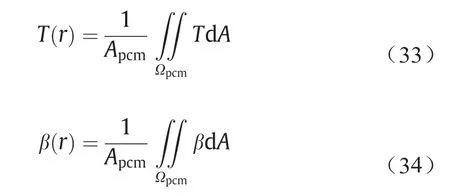
式中,Ωpcm代表圆柱截面上相变材料的区域;Apcm代表圆柱截面上相变材料区域的面积。
图9(a)和(b)分别展示了不同时刻下相变材料径向温度分布和径向液相分数分布。可以看到,不同位置处相变材料的温度和液相分数均不一致,意味着不同位置处相变材料的储热进程不一致。当t= 200 s时,除壁面附近外,其他径向位置上相变材料温度还未达到熔点,因此液相分数保持为0,此时相变材料还处于固态储热阶段。当t= 1200 s时,径向位置上相变材料的温度处于相变温度范围内,因此液相分数出现了很大的波动。值得注意的是,由于相变材料的相变温度范围为395.1~413 ℃,根据焓值法可知,每1 ℃的升温均会引起液相分数增加0.056。所以,虽然各位置处相变材料在相变过程时温度差别不大,但液相分数会发生较大幅度的变化。当t= 2400 s时,各个径向位置处相变材料的温度基本都超过了相变温度范围上限,所以此时液相分数几乎都为1,大部分相变材料处于液态储热阶段。
图10刻画了t= 600 s时距离壁面为0.5dp、dp、1.5dp和2dp的圆柱截面上相变材料的液相分数分布。首先可以发现,靠近入口处的相变胶囊中的相变材料熔化更快,并且熔化从换热流体的流动侧开始。其次,距离壁面为dp和2dp的圆柱截面上相变材料熔化更快,与图 9(b)中液相分数的分布情况相符。一方面,由于0.5dp和1.5dp对应的圆柱截面孔隙率低,圆柱截面上换热流体的流速相对较低,所以对流换热作用更弱;另一方面,0.5dp和1.5dp对应的圆柱截面上相变材料占比大,熔化需要的热量更多,所以储热进程更为缓慢。

图9. 相变材料不同时刻的径向分布。(a)温度;(b)液相分数。
3.2. 直径比对堆积床流动换热的影响
本节研究了具有不同直径比(4, 5, 6)的堆积床相变储热系统的流动特性和传热储热性能。入口温度Tin为465 ℃,质量流率为260 kg·h-1储热罐的内径为240 mm,高度为500 mm。为了便于分析比较,三个堆积床相变储热系统的储热量在设计时基本一致,并基于此确定了三个系统中所需的相变胶囊个数。三个不同直径比堆积床内相变胶囊的尺寸、个数和孔隙率等参数总结在表2中。图11展示了不同直径比堆积床的径向孔隙率分布,通过比较发现:具有不同直径比的堆积床对应于不同的径向孔隙率分布。从壁面到距离壁面1.5dp的范围内,三个堆积床的径向孔隙率的分布基本一致,但是越靠近罐体中心,径向孔隙率的差别越大。对于直径比为4的堆积床,容器的直径正好能够容纳4个相变胶囊,所以相变胶囊在罐体中心是以点接触或者不接触的形式排布,导致罐体中心区域的孔隙率很大。对于直径比为5的堆积床,容器的直径正好能够容纳5个相变胶囊,所以罐体中心被相变胶囊所占据,使得罐体中心的孔隙率几乎为0。对于直径比为6的堆积床,容器的直径正好能够容纳6个相变胶囊,理论上在罐体中心会与直径比为4的堆积床一样具有很高的孔隙率。但是直径比为6时壁面效应的影响减弱,罐体中心相变胶囊的排列具有一定的随机性,如图11所示。

表2 不同直径比的堆积床相变储热系统的参数

图10. t = 600 s时径向圆柱截面上相变材料的液相分数。

图11. 不同直径比堆积床的径向孔隙率分布。
图12(a)展示了具有不同直径比的堆积床的径向相对速度的分布,与径向孔隙率的分布基本一致。在近壁面区域,直径比为4、5、6的堆积床最大相对速度依次增大,分别为2.87、3.49和3.99。相变胶囊的直径随直径比的增大而减小,使得相变胶囊与壁面间的空隙变狭窄。由式(31)可知,当热空气流经狭窄的流道时,流速会增大。在中心区域,三个堆积床内相对速度的标准差分别为0.53、0.39和0.27,这意味着随着直径比的增大,堆积床中心区域流速变得更加均匀。
图12(b)展示了t= 1200 s时具有不同直径比的堆积床的相变材料径向液相分数的分布,能够观察到:直径比为4时堆积床近壁面处与罐体中心处相变材料具有最快的储热速度;而对于直径比为5和6的堆积床,近壁面处的相变材料的储热速度明显快于罐体中心区域的相变材料,这与径向孔隙率的分布是一致的。
图13展示了不同直径比堆积床相变储热系统的储热量与平均储热功率随时间的变化,直径比分别为4、5和6时系统的储热时间分别为121.03 min、89.73 min和79.80 min。由于三个储热系统在设计时的储热量基本一致,所以储热系统的平均储热功率随着直径比的增大而增大。直径比为4的堆积床中相变胶囊的直径为60 mm,而直径比为5和6的堆积床中相变胶囊的直径分别为48 mm和40 mm。小的直径对应更短的传热距离,因此储热进程能够加速。但是相变胶囊直径越小,堆积床的结构越紧密,这会引起堆积床内压降的急剧增大。计算结果显示,直径比分别为4、5和6的堆积床内的压降分别为142.97 Pa、213.34 Pa和257.13 Pa,这意味着维持系统运行所需的泵功依次增大。因此,当考虑将堆积床相变储热系统应用于实际场景时,需要综合考虑储热系统的储热时间、储热功率以及内部压降的大小等因素。
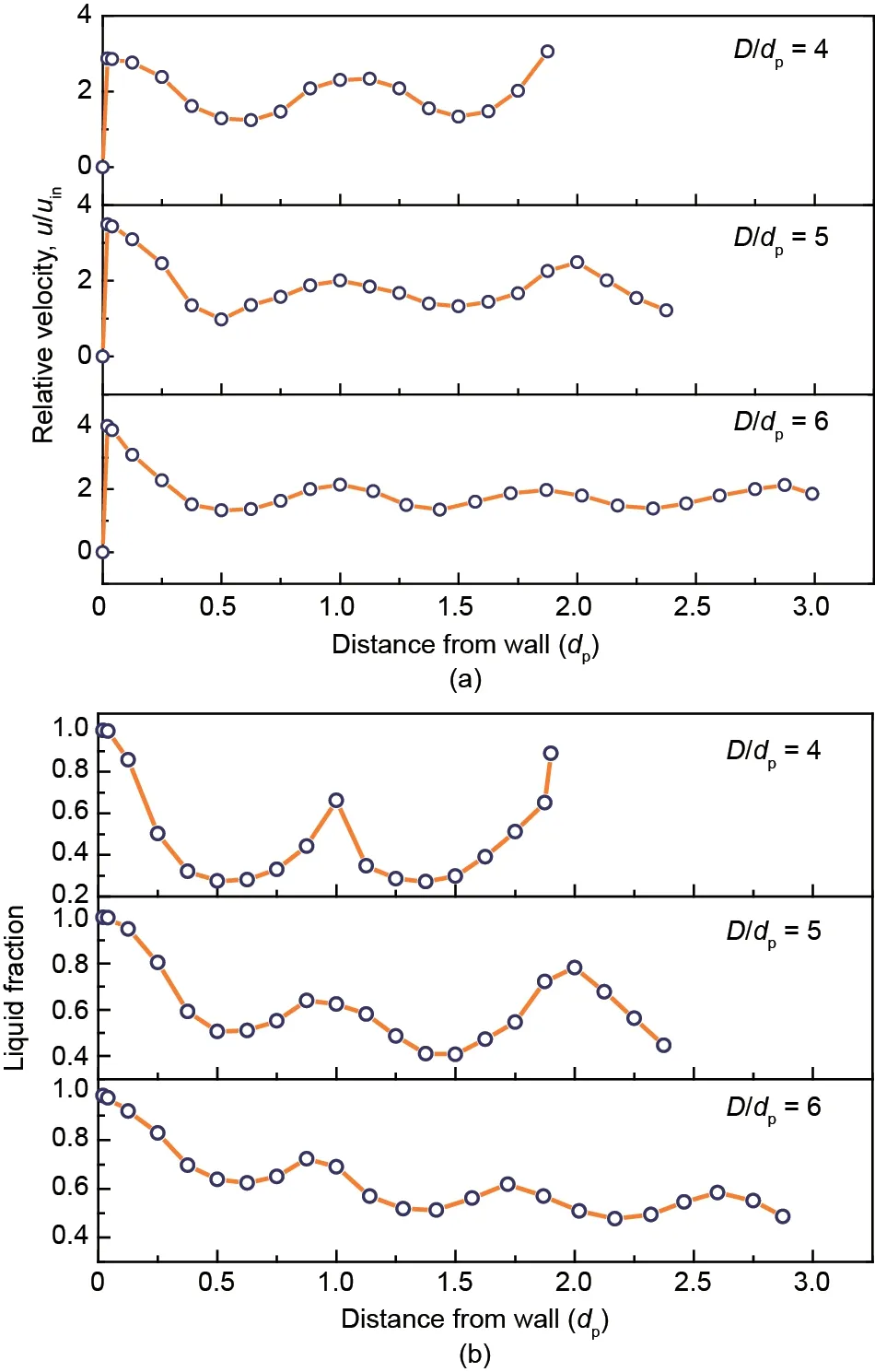
图12. 不同直径比相变堆积床LHS系统的径向分布。(a)相对流速;(b)t = 1200 s时不同直径比堆积床内相变材料径向液相分数分布。
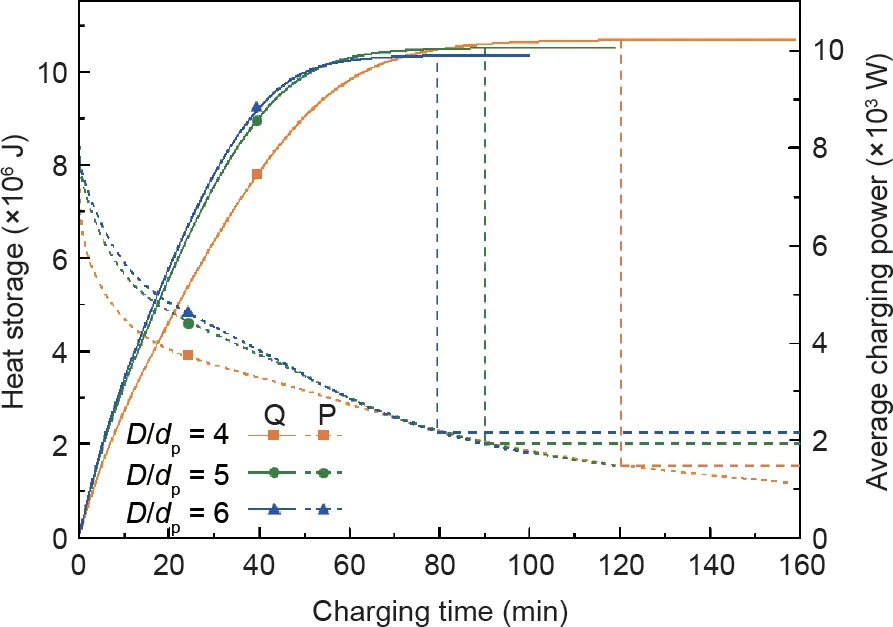
图13. 不同直径比堆积床相变储热系统的储热量与平均储热功率。
3.3. 雷诺数对堆积床流动换热的影响
基于直径比为5的堆积床相变储热系统,保持相变材料的史蒂芬数Ste=0.31,当换热流体的进口流量分别取220 kg·h-1、260 kg·h-1和300 kg·h-1时,堆积床的雷诺数Rep分别为4229.69、4998.72和5767.75。作出不同雷诺数下堆积床内相对流速的分布,发现三者的分布几乎重合,如图14(a)所示。经过计算得知,三种雷诺数下堆积床内近壁面区域换热流体的最大相对速度分别是3.40、3.49和3.55,而中心区域相对速度的标准差分别是0.40、0.39和0.39,这意味着雷诺数的增大对相对流速的分布几乎没有影响。但由于进口速度增大,堆积床内的径向流速发生成比例的提升,这将增强堆积床内的对流换热作用,从而加快相变胶囊的储热进程[图14(b)]。

图14. 不同雷诺数堆积床LHS系统的流动与热性能。(a)径向相对流速分布;(b)储热量与平均储热功率;(c)1200 s时径向液相分数分布。
图14(c)计算了不同雷诺数下堆积床相变储热系统的储热量与平均储热功率随时间的变化,随着雷诺数的增大,系统的储热量并不会改变,但是储热时间缩短了,储热功率相应提升。雷诺数分别为4229.69、4998.72和5767.75时堆积床的储热时间分别为97.53 min、89.73 min和83.63 min。但是,雷诺数的增大也会引起换热流体流动耗散的增加,从而增大进出口的压降,三个堆积床的压降分别为162.84 Pa、213.34 Pa和270.06 Pa。
3.4. 史蒂芬数对堆积床流动换热的影响
与上一部分类似,基于直径比为5的堆积床相变储热系统,保持雷诺数Re=4998.72,当换热流体的进口温度分别取445 ℃、465 ℃和485 ℃时,堆积床内史蒂芬数Ste分别为0.19、0.31和0.43。图15(a)为不同史蒂芬数下堆积床内相对流速的分布,发现三者的分布重合,这意味着史蒂芬数的改变对堆积床内流速的大小及分布均无影响,因此堆积床进出口压降的变化微弱。换热流体与相变胶囊之间的对流换热作用基本不变,但由于史蒂芬的增大代表着进口温度的增大,这将增大换热流体对相变胶囊的换热温差,从而增强相变胶囊的对流换热。如图15(b)所示,相变材料的储热过程均随着史蒂芬数的增大而增大。
史蒂芬数的增大意味着相变材料存储的显热增加,所以系统的储热量随之增加[图15(c)]。当史蒂芬数为0.19时系统的储热时间为99.20 min,当史蒂芬数增加至0.31和0.43时,储热时间变为89.73 min和84.7 min。所以,史蒂芬数的增大不仅能够提升储热系统的储热量,还能缩短系统的储热时间,因此能够很好地提升堆积床相变储热系统的热性能。
4. 结论
本文基于壁面效应引起的径向孔隙率振荡分布,建立了三维堆积床相变储热系统模型,通过将堆积床中相变胶囊温度变化的模拟值与实验对比,验证了模型的可靠性。本文研究了径向孔隙率振荡分布对换热流体的径向流速、相变材料的径向温度以及相变材料径向液相分数的影响。此外,还研究了不同的无量纲参数(如直径比、雷诺数和史蒂芬数)对换热流体和相变材料的影响,主要结论如下。
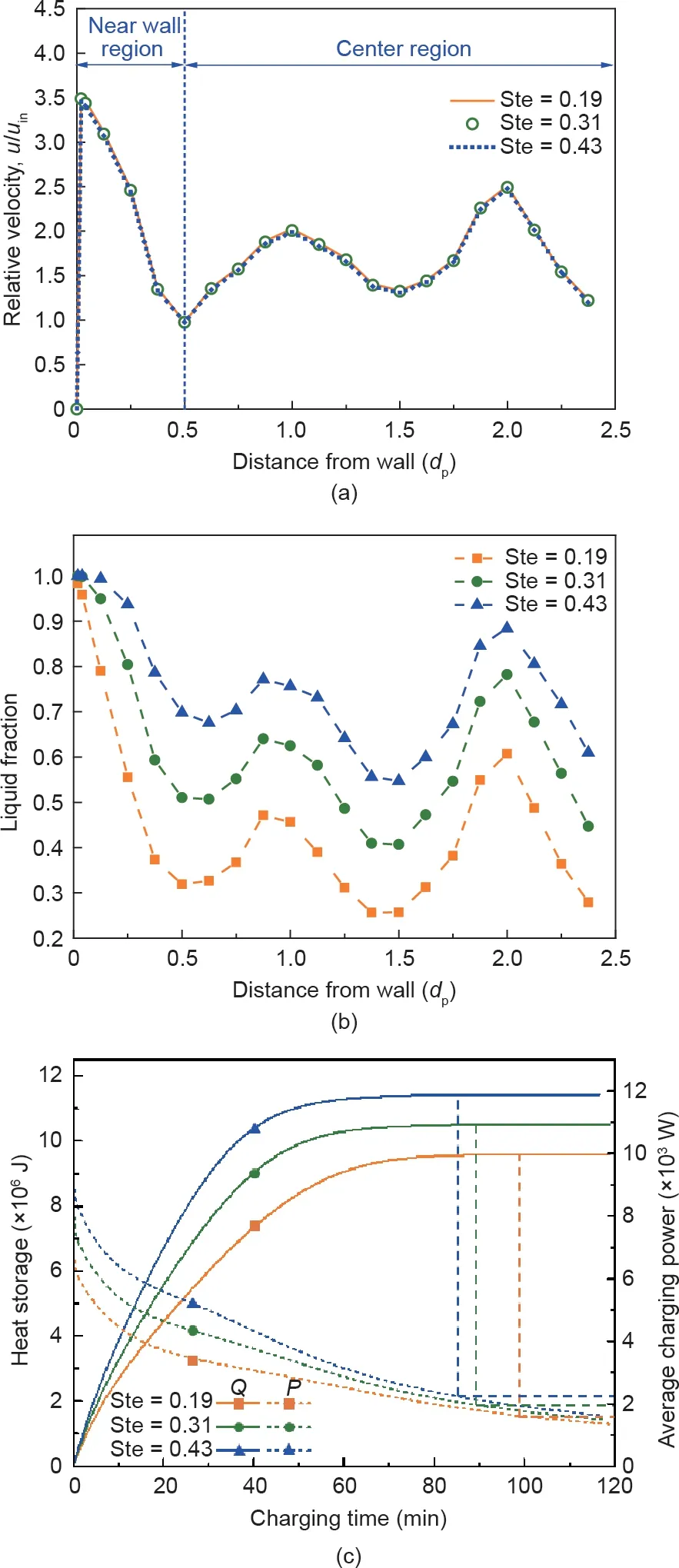
图15. 不同雷诺数堆积床LHS系统的流动与热性能。(a)径向相对流速分布;(b)1200 s时径向液相分数分布;(c)储热量与平均储热功率。
(1)通过沿堆积床径向截取了一系列的圆柱截面,直观地解释了径向孔隙率振荡分布的原因。当径向圆柱截面处的相变胶囊为点接触时,形成的空隙会造成高孔隙率,而当圆柱截面贯穿相变胶囊时,相变材料占据圆柱面上大部分区域,从而导致低孔隙率。
(2)径向孔隙率的振荡分布导致了换热流体流速在径向上的不均匀性,在近壁面区域,换热流体的流速急剧变化;而在中心区域流速的分布更为缓和,与径向孔隙率的分布一致。这也使得孔隙率大的地方相变材料熔化更快。
(3)随着堆积床直径比的增大,换热流体在近壁面区域的最大流速增大,但是由于相变胶囊的堆积变得更随机和致密,换热流体在中心区域的流速能够变得更为均匀。另外,直径比的增大能够缩短系统的储热时间并增大平均储热功率,但进出口压降会急剧增大。
(4)换热流体雷诺数的增大能够同比例地增大流速,从而加速相变材料的储热过程,并增大系统的平均储热功率。但是进出口压降的大幅提升表明,通过增大雷诺数来提升系统热性能需在泵功允许的范围内。
(5)相变材料史蒂芬数的增大对径向流速的大小和分布基本无影响,但是换热流体与相变材料之间温差的增加强化了传热过程,并能够提升系统的总储热量和平均储热功率。
致谢
本工作由国家自然科学基金创新研究群体科学基金(51521004)和国家自然科学基金(51906150)资助。
Compliance with ethics guidelines
H.B. Liu and C.Y. Zhao declare that they have no conflict of interest or financial conflicts to disclose
符号说明
V体积(m3)
A面积(m2)
r相变胶囊半径(m)
dp相变胶囊直径(m)
R储热罐半径(m)
D储热罐直径(m)
T温度(K)
H比热容(kJ·kg-1)
cp比焓(J·kg-1·K-1)
L潜热(kJ·kg-1)
E能量(J)
Ste史蒂芬数
q质量流量(kg·s-1)
u流速(m·s-1)
u′相对流速
Rep孔隙雷诺数
t时间(s)
x距离(m)
z高度(m)
p压力(Pa)
k湍动能(m2·s-2)
c1, c2湍动能方程的模型常数
c湍流黏性关系的模型常数
Q储热量(J)
P储热功率(W)
s相对流速的标准差
φ孔隙率
ρ密度(kg·m-3)
λ导热系数(W·m-1·K-1)
μ黏度(kg·m-1·s-1)
μt湍流黏度(kg·m-1·s-1)
σT能量方程普朗特数
σk湍动能方程普朗特数
σε湍流耗散率方程普朗特数
ε湍流耗散率(m2·s-3)
β液相分数
γ湍流模型系数
Ω换热流体或相变胶囊区域
下标
i,j坐标方向
f 换热流体
PCM 相变材料
total 总量
shell 相变胶囊外壳
tank 储热罐罐体
stored 已存储的热量
charge 储热过程
aver 平均值
in 进口
0 初始状态
l 液态
s 固态
