基于张量因子分解框架的航班延误模式分析
2021-08-13张明远陈莘文孙立君杜文博曹先彬
张明远 ,陈莘文 ,孙立君 ,杜文博 ,*,曹先彬 ,*
© 2021 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
1. 引言
随着世界民用航空业的飞速发展,严重的航班延误仍然是一个重要问题。航班延误不仅使乘客不愿考虑航空交通或再次选择同一家航空公司[1-4],而且迫使航空公司承担飞机维护和机队利用率不足的额外费用[5]。此外,航班延误导致燃油消耗和二氧化碳排放量增加,对环境造成了极大危害[6,7]。除了上面列出的直接影响外,航班延误对整个社会经济发展都具有负面影响[8]。
许多因素使得此问题变得更复杂和棘手,这些因素通常为异常天气[9]和技术原因[10],其中技术原因主要包括空中交通管制[11]、设施容量不足或者调度不当[12]、运行程序更改[13]和缓冲时间不足[14]等。因此,挖掘潜在的航班延误模式并设计适当的策略非常困难[15]。最近,基于历史观测数据的分析方法已被证明不受上述约束影响并适用于包含隐藏信息的动态数据[16]。因此,促进系统认知和决策的方法是充分利用历史数据[17]。例如,当遇到恶劣天气时,可以查询天气条件相似的过去几天,并参考当日空中交通管制员采取的行动。近期的几项研究[18-23]致力于发现空中交通管理中的固定模式。Liu等[19]介绍了一种半监督学习算法,可以将相似的日期划分为不同的模式。第一步先量化每小时航空天气预报数值之间的距离(表示相似性),然后确定总距离较小的日期。他们应用此方法在纽瓦克自由国际机场(EWR)进行了两个案例研究,并证明了其有效性。Mukherjee等[20]也提出了一种根据航空天气条件对运行模式进行分类的方法。他们使用天气指数作为输入并应用因子分析来确定主要的天气模式,然后,使用Ward的最小方差法将日期聚类。属于同一模式的日期共享相似的天气模式。除天气条件外,一些研究还试图从其他角度确定相似的日期。Grabbe等[21]使用k-means聚类算法来识别地面延误程序中的相似日期,并对地面延误程序的开始和结束时间以及计划的到达率数据应用期望最大化(EM)算法。其他类似的研究主要关注空中交通流量和航班延误以确定相似的模式[24]。Gorripaty等[17]测量了需求和容量数据中的主要成分,但对数据进行聚类分析后发现,需求或容量中没有固定的模式。通过确定国内直飞航班到达延误的周期性模式,Abdel-Aty等[25]发现统计方法未能有效检测某些模式。
尽管做了一些研究,但是这些研究在理解航班延误模式方面仍然存在差距。如上所述,一种有效的方法是在时空历史数据中找到聚类模式[26,27]。但是,由于该数据的高维特性,其很难在欧式空间中找到明显不同的模式[28]。因此,后续研究提出了潜在成分分析的方法来揭示隐藏的模式,诸如潜在分布分析[29]、潜在特征分析(包括响应理论和Rasch模型)以及层次分析等方法,可以利用从张量分解中获得的特征来形成投影和维度较低的子空间,以增强时空交通动态模式的底层聚类结构[30]。这些方法开辟了交通科学领域的新方向[31],如城市流动性分析[32-34]、交通速度预测[35]、交通数据缺失[36,37]和船舶航迹恢复[38]。
受上述方法的启发,本文的主要研究目标是使用大量的空中交通数据来了解潜在的空中交通和航班延误模式。首先将飞行记录数据视为从泛分布中抽取的多元观测概率数据,将概率分解问题等价为Tucker潜在类别分析模型来挖掘主要模式。然后,提出一个估计模型用于在已知信息极少的情况下判定延误程度。本文的其余部分安排如下:第2节介绍模型框架;第3节展示一个基于中国航空数据的案例研究;第4节给出主要结论。
2. 模型框架
本节介绍了以概率为基础的飞行数据建模的总体框架。目的是从不同角度描述空中交通和航班延误的主要模式及其相互作用。第2.1节介绍了在框架中使用的数据表示方法;第2.2节提出了一种非负Tucker分解(NTD)方法;第2.3节描述了潜在类别分析(LCA)方法。
2.1. 数据表示
我们令xa= (xa1, ...,xaq)T代表一个飞行记录a,其中q代表维数,即单个行程记录中的属性维度。为了表征航班的特征,每个元素可以表示航班的离港机场(xa1)、离港时间(xa2)、离港日期(xa3)、延误程度(xa4)等。
为方便起见,将这些值映射为离散值。xaβ∈{1, ...,wq}为属性β(β= 1, ...,q)从1开始的离散值。β表示属性的索引。wq表征维度为q的离散值向量。以离港机场为例,对于记录a来说,xa1= 1代表机场1。xa2∈{1, ...,24}表示航班的离港时间,每个值对应一天中的一个小时。然后,使用4年(2014—2017年)的飞行记录数据介绍我们的方法,其中所有航班的离港日期按时间顺序编号为xa3∈{1, ..., 1461}。由于到港延误与空中航班时段密切关联,可能会受到空中飞行加速、减速的影响,因此本文考虑采用离港延误而非到港延误来研究航班延误模式,以更好地反映目标机场的运行状态。根据美国联邦航空管理局(FAA)制定的规则及相关研究,延误航班是指比计划时间晚15 min以上起飞的航班。考虑实际情况,本文选择较计划离港时间晚45 min和90 min作为阈值。因此,本文将每个航班的离港延误分为4个级别:① < 15 min;② 15~45 min;③ 45~90 min;④ > 90 min。我们分别用xa4∈{1, ..., 4}表示“准时”“轻度延误”“中度延误”和“重度延误”。
2.2. 非负Tucker分解
已有研究表明,张量分解在各种情况下都显示出许多优点,尤其是当必须将数据分解为加性成分之和时[39]。张量分解最早由Tucker [40]在1963年提出,非负NTD [41,42]是在张量分解基础上获得的,用于处理自然数据的非负观测值。NTD是一个强大的工具,可以从高维张量数据中提取基于非负数部分的潜在分量,同时保留数据的多线性结构[24]。从数学维度来说,它将张量分解为一组矩阵和一个核心张量。
给定K阶张量χ,NTD将任意一个非负K阶张量R+是正实数空间;K是空间维度;I是正交基)分解为非负核心张量(J是正交基)和K个非负矩阵的模积
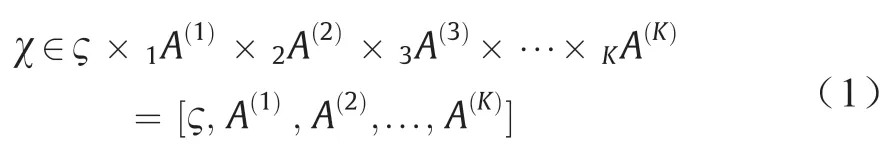
式中,A(1),A(2),A(3), ...,A(K)被称为因子矩阵;ς是核心张量,显示了不同因子矩阵之间的交互作用和连接程度。在这种方法中,核心张量ς和因子矩阵A(K)在元素上为非负数。具体如下:


式中,F为矩阵范数。
2.3. 潜在类别分析
潜在类别分析是一种统计方法,可从多元分类数据中找到潜在类别[43,44]。潜在类别模型公式如下:

式中,Pi1,i2,...,iN表示概率分布方程;i是维度指标;T是每个维度类别的模式数量;N是维度数量;t是每个维度模式的索引;pt是加为1的概率是条件概率;∂和μ是概率矩阵的维度。潜在类别分析通过条件独立性的标准来定义潜在类别。这意味着每个变量在统计上独立于每个潜在类别中的每个其他变量。因此,可以将概率张量中的每个元素计算为所有模式组合的总和。
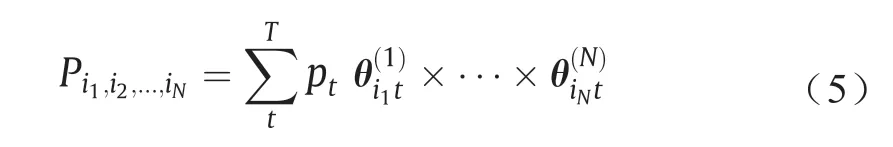
式中,θ(N)是表示模式N的概率向量。
在本研究中,我们使用了潜在类别模型,该模型假设每个观察值都是由基础类别的混合生成的,并且每个类别都与唯一的概率分布相关。因此,联合分布被认为是乘积多项式与观测概率的混合。使用第2.1节中的符号,可以将所有飞行记录x汇总为一个维度φ=w1×w2×... ×wm的m阶张量,并且张量中的每个单元格(v1,v2, ...,vm)(v代表张量的一个维度)都是对飞行数量∑δ(xa1=υ1, ...,xam=υm)的计数。δ是一个二值的指示函数,δ= 1为真,δ=0为假。为了更好地理解数据集的内部联系,我们将这些飞行记录放入一个概率张量中,其每个值代表一个飞行记录属于该坐标的概率。每个值的概率张量表示属于特定单元格的飞行概率pc(xa1=υ1, ...,xam=υm)。观测概率(也是概率质量函数)可以通过Tucker分解以类似的方式重新生成。

核心张量π捕捉了不同维度模式之间的交互性。是概率因子矩阵,代表了维度N的主要模式。可以将概率张量中的每个元素计算为所有模式组合的总和。

3. 案例研究
3.1. 航班运行数据
本文分析的数据集由中国民用航空局(CAAC)提供。鉴于本文的研究目的是为空中交通和机场管理提供决策支持,因此航班延误情况是本文研究重点。而且,空中交通流量是延误情况的基础。因此,本文选择空中交通流量和航班延误作为主要研究对象。选择离港延误是因为其可以更好地反映离港机场和空域的拥挤程度。表1列出了航班数据的分类值。该数据库包含13 492 326架国内航班。所有航班共连接224个机场,其中北京首都国际机场的航班数最多,占所有机场航班数的6.3%。航班的出发日期为2014年1月1日—2017年12月31日,出发时间可以为一天之内的任何时间。可以看出,根据出发延误时间可以将所有航班分为4组。4个组中的航班数占比分别为37%、38%、14%和11%。这些航班的平均离港延误时间为31.08 min。2008年2月9日是航班数量最多的一天,为12 419架次。2014年1月1日是航班数量最少的一天,为7009架次。机场最为繁忙的时间段是8:00~9:00,其中有6%的航班在此时间段内起飞。

表1 飞行数据的分类值
3.2. 张量分解
本文假设飞行记录是从通用分布中采样的多元变量。将13 492 326次飞行记录汇总为同一张量。每个观测值包含4个变量,包括离港机场、离港日期、离港时间和延误程度。总组合为224 × 1461 × 24 × 4。在这里,我们使用一个大小为3(离港机场,A)× 4(离港日期的编号,D)× 5(一天中的时间,H)× 4(延误程度,L)的核心张量π来捕获不同模式间的相互作用。尽管更大的核心张量可以包含更多信息并反映不同模式之间的全面关系,但是较小的核心张量可以促进对结果的解释。此外,现有研究表明,结果在不同尺寸的核心张量上基本一致[48]。在下文中,我们将以核心张量大小[3 × 4 ×5 × 4]为例介绍主要结果。
图1(a)描绘了5个模式的离港时间分布。模式H1占所有航班的18.7%,其从11:00开始逐渐上升,并在24:00达到峰值。模式H2与高斯分布的形状相似,其在17:00达到峰值,并且该模式占据所有航班的24.4%。与H1和H2相比,H3和H5分布更加集中。它们在早上显著增加,到中午突然下降。模式H4在11:00达到峰值,然后在一天的其余时间连续下降。H3、H4和H5的比例分别为22.9%、22.2%和11.8%。离港日期的因子矩阵由1461行和4列组成,这些因子矩阵描述了原始离港日期和离港日期模式之间的对应关系。我们分析了一年中不同月份和一周中不同日期的模式,并汇总了一年中不同月份和一周7天的日期模式的分布概率,以确定流量分布如何与离港日期交互。一周7天的日期模式如图1(b)所示。模式W1集中在工作日,而模式W3的峰值出现在周末两天。模式W2和W4则呈现相反趋势。W2主要集中在星期一、星期六和星期日,模式W4主要集中在星期三、星期四和星期五。图1(c)显示了不同月份的模式。我们可以观察到明显的季节多样性。模式M1主要集中在秋冬季,而模式M2主要集中在冬季和春季。模式M3集中在春季,而模式M4主要分布在夏季,夏季是航空系统的旅行高峰时段。

图1.不同维度的主要模式。(a)每个模式(列)的离港时间在因子矩阵中的概率分布Probability(H);(b)离港日期在星期几的概率分布Probability(W);(c)离港日期在月份的概率分布Probability(M)。
虽然上述计算过程未考虑任何空间位置信息,我们仍可以通过机场的地理位置来识别这些模式的特点。作为中国的交通枢纽,北京首都国际机场以A1和A2模式为主。此外,模式A1主要分布在东南部地区,而模式A2主要分布在西南部地区。模式A3主要由中西部地区的机场组成。
图2显示了延误程度因子矩阵中每个模式(列)的延误程度的组成。L1、L2、L3和L4代表不同延误程度的航班,从“准时”到“重度延误”(如2.1节所述)不等。与原始张量相比,延误程度模式几乎保持不变,但存在不同延误程度的航班。图2显示了每个延误程度模式的组成,分别占总样本数量的40.7%、10.5%、29.1%和19.7%。应当指出,延误是空中交通拥堵的一种表现,因此延误程度与时空因素中的交通流量特性密切相关。为了进一步分析,我们采用延误程度模式和其他模式之间的条件概率来研究相互作用。我们根据贝叶斯定理计算条件概率分布Probability(L|H)。给定离港时间模式,延误程度模式的条件分布为:

Probability(L|H)显示了延误程度模式如何与离港时间模式交互。可以看出,模式L1表示“准时”时间与所有模式密切相关,这表明“准时”航班在一天中的任何时候都占据主流。H1表示全天呈上升趋势的飞行流量模式,与延误模式L2相关联,后者对应“轻度延误”的航班。H2主要由离港时间模式L3和L4覆盖,表示高等级延误与下午的流量高度相关。H3、H4和H5主要由L3和L4覆盖。这可以用以下事实来解释:由于大多数机场的空中交通繁忙,早晨离港高峰期间的航班可能会“重度延误”。

图2. 延误因子矩阵中每个模式(列)的延误程度概率Probability(L)。

根据离港时间模式和延误程度模式的因子矩阵,我们发现在M1/W1、M2/W2和M3/W3中,“准时”和“轻度延误”模式最多。但是,M4/W4表示流量主要集中在工作日和夏季,并且往往会出现“重度延误”。

如式(10)所示,机场模式也与延误程度模式相关。显而易见的是,模式A3主要由L1覆盖,这可能表示中西部地区机场的空中交通延误较少。与A3相比,A1和A2更可能产生“重度延误”,这可以用中西部地区机场相对较少的交通流量和充足的空域资源来解释。如上面的分析所示,延误受时间和空间的影响很大。为了进一步探讨模式之间的相互作用,我们提出了沿时间和空间维度的模式关联。如图3所示,(L2,H1)的值大于A1中其他单元格的值,这表明当下午或傍晚的航班从东南部地区的机场起飞时,它们会稍有延误。我们还在(L3,H3)的A2模式内观察到大量飞行流量,而这种流量很少出现在A1和A3中。由此可知,在上午高峰期,从西南部地区机场起飞的航班通常会有“中度延误”。如前所述,由于中西部地区机场(A3)的运力过剩,航班延误的可能性很小,此现象与A3中的单元格(L1,H2~H4)一致。

图3.不同机场模式的延误程度和离港时间的关联。
实际数据表明,张量分解能够使我们解释基于潜在因素的复杂依赖性和高阶相互作用。核心张量π以非常有效且信息丰富的方式描述了不同模式之间的交互。该框架有助于我们理解和解释大型数据集中模式之间的潜在相互作用和复杂依赖性,从而加深我们对空中交通管理的理解。
在此基础上,存在另一个重大问题。如果仅考虑从时间和空间信息中提取的有关潜在模式的信息,是否可以估计延误程度?尽管以前的研究表明,航班延误可归因于许多复杂因素[49],但这一问题可能具有重大意义。首先,由于各种延误原因的共同作用,产生了基于历史信息的潜在模式。例如,夏季极端天气频繁发生,并且夏季与严重的延误模式有强烈的相互作用。其次,由于时空信息不要求我们详细了解运行特性,因此,仅离港时间和离港机场等基本信息就可以帮助我们事先对延误进行初步评估。第三,航空系统的高度动态性和复杂性使人们相信,无法通过基本信息来估计延误。因此,如果实现了准确的估计,那么我们的框架所产生的潜在模式的有效性也得到了证明。由于该框架对这个问题的适应性,为了进一步探索,本研究采用随机森林(RF)算法来构建估计模型[50]。RF的优点包括:①可以对泛化误差产生内部无偏估计;②可在大型数据库上高效运行;③具有对变量之间相互作用进行建模的能力[51]。具体来说,RF是B颗树的集合{Γ1(X), ...,ΓB(X)},其中X= (x1, ...,xρ)是描述符的ρ维向量。集合产生B个输出其中是第b颗树的估计。汇总所有树的输出以产生一个最终估计对于分类问题,是大多数树估计的类别。模型训练程序如下:
(1)准备训练数据。准备训练数据的ρ维样本及其类别标签。
(2)选择参数。E:每棵树的最大深度;C:分割内部节点所需的最小样本数;V:每次拆分的变量;ML:在叶节点处需要的最小样本数。
(3)增长分类树。对于b= 1~B,从训练数据中绘制一定尺寸(Sd)的引导样本Z*。使用大约2/3的原始训练样本生长分类树,将剩下的1/3样本保留为所谓的袋外(OOB)样本。
(4)树的生成。对于每个引导样本,进行下述过程以生成一棵树Γb(X)。在每个节点上,选择最佳变量/分割点,并将该节点拆分为两个节点,直到该节点的样本数小于C,该树将增长到最大尺寸E,而不会被修剪。重复上述步骤,直到B颗树长出。
(5)结果输出。通过将树的估算值与森林中所有类似树的多数投票进行汇总来估算新数据。输出其中是对第b颗树的估计。
为了评估估计模型的性能,使用4个指数,参考式(11)~(14)。F1macro为宏平均数,用于对所有类别(1,...,u)加权平均。F1micro为微平均数,用于对所有样本平均加权,从而有利于样本预测结果的提升。加权分数在每个标签中找到平均值,然后按每个类的真实实例数加权。AccuracyOOB是训练样本集Z*的平均准确度,仅使用其引导样本中没有的树[52]。

式中,Pmacro是宏精确率;Rmacro是宏召回率。Precisionu表示TPu数除以TPu和FPu的总数(TPu是类别u中将正类正确预测为正类的数量,FPu是类别u中将负类错误预测为正类的数量),而Recallu定义为TPu数除以TPu和FNu的总数(FNu是类别u中将正类错误预测为负类的数量)。

式中,Pmicro是微精确率;Rmicro是微召回率。

式中,Su是类别u中的样本数量;S为样本数量。
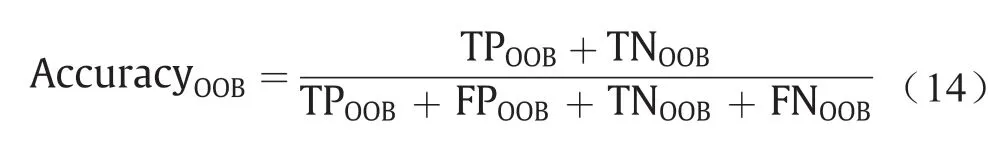
式中,TPOOB是OOB样本中将正类正确预测为正类的数量,FNOOB是OOB样本中将正类错误预测为负类的数量。FPOOB是OOB样本中将负类错误预测为正类的数量,TNOOB是OOB样本中将负类正确预测为负类的数量。
本研究使用了潜在的时空模式数据。分类问题涉及识别4个延误程度(“准时”“轻度延误”“中度延误”和“重度延误”)。为了估计模型在实际中的执行效果,本文采用了交叉验证策略。一轮交叉验证涉及将所有记录分为5个互补子集,其中对4个子集执行训练过程,然后在另一个测试集上验证分析。接下来,将验证结果在5个回合中取平均值,以估算模型的性能。总共使用了13 492 326条记录。如上所述,选择每种模式下的飞行概率值(潜在的时空模式)作为特征,即{A1~A4,H1~H5,W1~W4,M1~M4},每个功能的范围是0~1。
树的数量是最重要的变量,其应该足够大以使RF的泛化误差收敛。在图4中,我们发现当B从100增加到150 时,AccuracyOOB从53.1%变为53.4%;当B大于150 时,AccuracyOOB稍微增加。在B大于150后,RF分类器对B的增加几乎不敏感。为了获得更好的参数集,本文使用了网格搜索方法,即通过尝试其他参数的若干种组合来确定此模型的最佳参数值。
各个类别的整体性能和准确性如图5所示。正如先前的研究所指出的,由于延误主要由动态操作因素决定,因此难以在延误发生之前做出准确判断[53,54]。我们的模型仅考虑通过基本飞行信息揭示的潜在模式,在这种情况下,RF的所有性能指标均达到50%以上,各个类别的准确度分别为60.0%、46.0%、44.0%和65.0%,这是一个非常积极的表现。它表示可以仅根据时间和机场信息预先估算不同航班延误的概率。“准时”模式和“重度延误”模式由于具有独特的特征而被更准确地分类。即使该算法在分类“轻度延误”和“中度延误”类别时比较困难,但混淆矩阵对角线附近的深色区域表示错误的估计值具有较小的偏差。

图4. 树的数量对模型性能的影响。

图5. 分类结果。(a)不同指标衡量的总体表现;(b)混淆矩阵。
4. 结论
在本文中,我们开发了一个概率分解框架,该框架可将大量飞行记录数据转换为时空高维张量。我们的目的是调查空中交通和航班延误的时空动态模式。我们假设每个飞行观测都是从泛分布中产生的样本。然后,我们使用非负张量因子分解方法进行数据处理。结果表明,清晰的模式可以被挖掘出来。核心张量也有效展示了不同模式的相互作用,解释了延误与时空模式之间的关系。另外,“重度延误”往往发生于每一天的下午,尤其是工作日和夏季的高峰期。从中西部地区机场起飞的航班在一天中的任何时间都很少有延误的可能性。
通过在空间和时间维度上加强对航班的了解,该框架可以为航班延误的建模提供启发。而且,本文已经证明潜在模式对延误有一定作用。随着空间和时间信息的整合,潜在的模式可以给出有关延误程度的估计结果。在高度动态的环境和延误复杂性的背景下,此结果使我们对空中交通和航班延误与时间和空间的相互作用有了新的认识。该框架通过潜在类别模型和概率分解方法对海量航空数据进行深入了解。研究结果可以帮助机场运营商和空中交通管理人员,根据从历史情景中获得的经验,更好地制订空中交通管理策略和完善机场内部管理。未来可以进一步研究涉及更多因素(如天气和航线属性)的相互作用的航班延误问题。
致谢
感谢美国南佛罗里达大学的张瑜博士和美国卡内基梅隆大学的张沈麒对本文撰写工作给予的支持和建议。该研究获得国家重点研发计划(2019YFF0301400)及国家自然科学基金(61671031、61722102和61961146005)资助。
Compliance with ethics guidelines
Mingyuan Zhang, Shenwen Chen, Lijun Sun, Wenbo Du, and Xianbin Cao declare that they have no conflict of interest or financial conflicts to disclose.
