单相接地故障下MMC入网电流耦合机理分析及小信号建模
2021-08-12黄萌车江龙查晓明刘浴霜盛举
黄萌, 车江龙, 查晓明, 刘浴霜, 盛举
(武汉大学电气与自动化学院,湖北 武汉 430072)
0 引言
相比于两电平、三电平电压源换流器(voltage sour ce converter,VSC),模块化多电平换流器(mo du lar multilevel converter,MMC)以其模块化设计、谐波含量低和输出电压等级高等优点[1—6],在高压直流输电领域应用广泛。我国已经投运的上海南汇、广东南澳、浙江舟山等柔性直流输电工程均采用MMC拓扑结构。
MMC系统安全稳定运行是当前的研究热点。当交流侧发生不对称故障,如电压不对称跌落和单相接地故障等时,产生的负序分量会给系统带来一系列负面影响,如输出电压、电流波形畸变等,此时通过引入双序电流控制可很好地改善电流波形质量[7—8]。同时,针对故障引起并网点电压下降的问题,诸多文献提出通过注入无功电流支撑电压的控制策略。文献[9—10]提出根据电压跌落程度和电网阻抗生成无功电流指令值。文献[11—12]通过分析功率与电流的关系,实现电压抬升及电流限幅。
对于不同的交流侧故障,电压不对称跌落下通过相序分离得到的交流侧等效双序回路模型相互独立,而在单相接地故障下,接地阻抗的存在会将各个序网络连接起来,使得各序回路之间相互作用。因此,无功电流的注入还需考虑序网络间的耦合特性,同时交流侧阻抗的改变也会对整个系统的稳定性产生不同影响。
目前常采用小信号建模方法进行系统级稳定性分析,文献[13—14]基于平均开关函数模型建立考虑内部动态行为的MMC系统小信号模型,并进行相应的模态分析。文献[15]建立基于广义动态相量的小信号模型,并考虑换流器内部高阶谐波的作用。上述研究均建立于无外部故障扰动的情况,而当交流侧发生不对称故障时,系统内部产生的谐波序分量和用于改善波形质量新增的控制环节会增加建模的复杂性。文献[16—18]建立三相对称与不对称电压跌落下VSC系统的小信号模型并进行动态特性分析。文献[19—20]基于不对称电网电压条件下的MMC系统小信号模型,分析新增负序电流控制器对稳定性的影响。
为了更好地研究单相接地故障下阻抗参数和电流耦合特性对MMC系统稳定性的影响,文中首先基于交流侧等效模型分析双序网络间的耦合关系,然后建立对应工况下MMC系统的小信号模型,并分析阻抗变化和电流注入对稳定性的影响过程,最后给出定量分析结果并进行仿真验证。文中所提分析方法从稳定性角度为单相接地故障下MMC系统的参数设计和电流注入策略制定提供了一定参考。
1 单相接地故障下MMC系统结构
1.1 MMC系统拓扑
单相接地故障F下并网MMC系统拓扑如图1所示。MMC通过Y-△连接的变压器与非理想电网相连。Udc为直流电压源;Ug为电网电压;Zg为交流系统等效阻抗;Us,Is分别为端电压和交流电流;Lf为滤波电感。

图1 单相接地故障下并网MMC系统拓扑Fig.1 Grid-connected MMC system topology under single-line to ground fault
MMC三相拓扑如图2所示,每一相包含上、下2个桥臂,每个桥臂由N个子模块(SM)、桥臂电阻R0和电感L0串联组成。C,Ceq分别为单个子模块电容和单个桥臂的等效电容,Ceq=C/N;uarm,iarm分别为桥臂电压和桥臂电流;iuj,ilj分别为上、下桥臂电流,j=a,b,c;usm,ism分别为子模块电容电压和电流;Idc为直流电流;S为平均开关函数,表示子模块的投入比例。MMC可以通过控制子模块的投切,快速调节输出多电平交流电压。
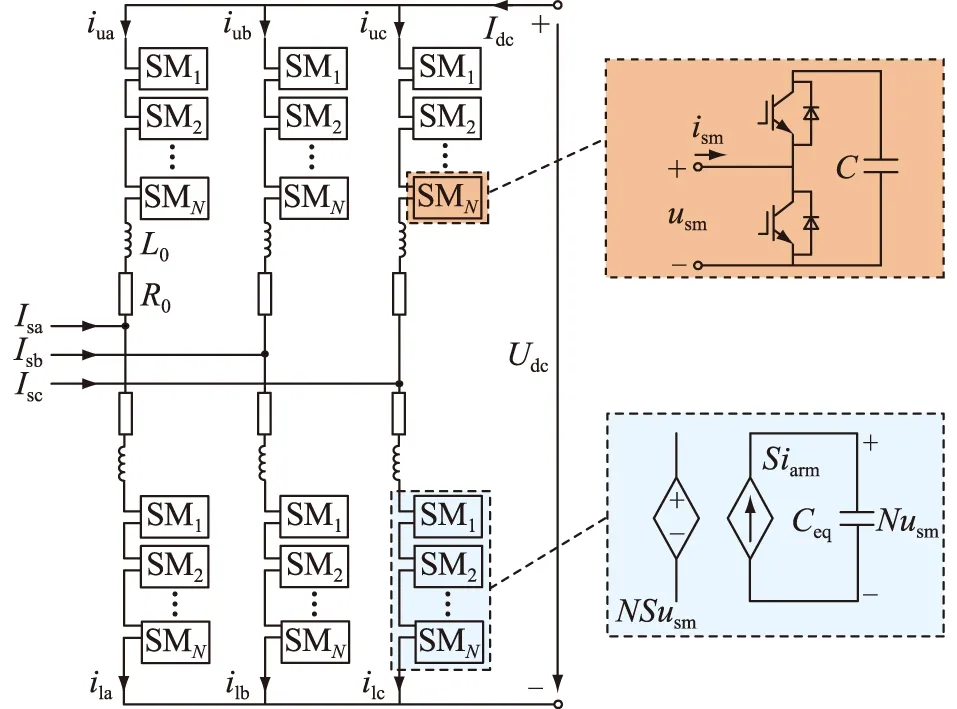
图2 MMC三相拓扑Fig.2 The topology of three-phase MMC
1.2 MMC系统交流侧等效模型
假设单相接地故障发生在a相,则图1的等效模型和合并后的各序电路分别如图3、图4所示。ZF为接地阻抗;ZT为变压器等效阻抗;上标+,-,0分别表示正序、负序和零序。

图3 单相接地故障下并网MMC系统等效模型Fig.3 Equivalent model of grid-connected MMCsystem under single-line to ground fault

图4 单相接地故障下的序电路Fig.4 Sequence-domain circuit under single-line to ground fault
由图4可知,ZF将各个序网络连接起来,导致各个序网络之间相互作用。变压器采用Y-△连接方式,故交流电压和电流不存在零序分量。系统主要电路参数如表1所示。

表1 MMC系统主要参数Table 1 Major parameters of MMC system
由图4可得正序、负序电压分别如式(1)、式(2)所示。此外,文中还考虑了变压器对电压、电流相移的作用:在正序网络中,Y侧电压/电流比Δ侧电压/电流超前30°,而在负序网络中则刚好相反。
(1)
(2)
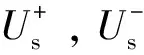
(3)
将e-jθs代入式(1)、式(2),其中,θs为锁相环输出相位,转换至dq同步旋转坐标系下:
(4)
(5)
(6)
(7)

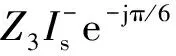
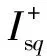

图5 单相接地故障下的低电压穿越过程Fig.5 Low voltage ride-through process under single-line to ground fault
2 小信号模型建立
由于MMC子模块电容的分散布置,各个子模块在充放电过程中会出现电容电压波动的情况,进而导致桥臂电流出现二倍频为主的谐波分量。实际上,usm和iarm的谐波构成了MMC的内部动态特性,为建立状态空间模型提供了基础。
为了简化电路分析,假设同一桥臂上的所有子模块可以等效为一个受控电压源,如图2所示,且在排序均压算法下所有usm均相等,则usm,uarm,iarm间的关系为[21]:
uarm=NSusm
(8)
(9)
在实际应用中,常采用最近电平调制方法控制子模块投切。在不平衡电网条件下,为了改善输出波形质量,部分调制信号还会由引进的负序电流抑制器产生,则上、下桥臂平均开关函数Su,Sl可表示为:
(10)

假设MMC的等效开关频率足够高,忽略usm中高于三倍频的分量,则usm可表示为:
(11)
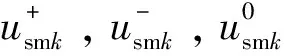
交流侧电流无零序分量,但零序分量仍存在于桥臂的二倍频环流中,导致直流侧功率波动。因此上、下桥臂电流表示为:
(12)

将式(10)、式(12)代入式(9)中,可得到usm各分量的状态方程。同理,将式(10)、式(11)代入式(8),并将所得方程与交直流侧电路的KVL方程相结合,即可求出iarm各分量的状态方程。因此,基于usm和iarm的状态方程即可建立MMC的状态空间模型。
MMC系统控制框图如图6所示。相序分离环节中采用同步相位和对称分量实时检测方法[22],将采集到的三相交流电压和电流变换到αβ参考坐标系下,然后将该αβ分量和相移90°后的分量通过图6所示的矩阵转换成正负序分量。根据图6的控制系统框图,可以得到各控制器的状态方程。
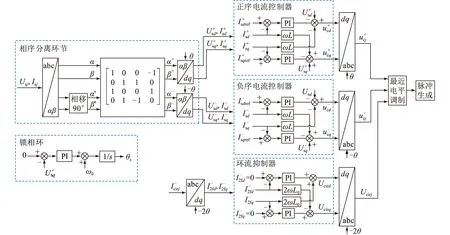
图6 交流侧不对称情况下MMC系统控制框图Fig.6 Block diagram of MMC control system under unbalanced grid conditions
文献[15—16]具体给出了MMC和控制系统的状态空间方程,此处不再赘述。将MMC与控制系统的状态方程在某一稳态工作点进行线性化,再与式(4)—式(7)线性化后的表达式合并,得到MMC系统的小信号模型为:

(13)
式中:A,B分别为状态矩阵和输入矩阵;Δx为状态变量;Δu为输入变量。
3 系统参数对稳定性的影响
文中主要分析阻抗、电流参数改变使系统失稳的机理,然后利用李雅普诺夫稳定性判据分析参数变化时MMC系统的小信号稳定性。即由式(13)求出的所有特征根的实部均为负时,系统在该运行点处受到扰动可以恢复稳定;而当至少一个特征根的实部为正时,系统在该运行点处受到扰动会失稳。
3.1 阻抗参数对稳定性的影响
交流侧阻抗大小影响锁相环的动态特性,进而影响系统的动态特性。单相接地时,ZF改变了系统交流侧的拓扑结构,使得各序电网阻抗之间、Zg与ZF之间相互耦合,如式(3)所示,共同影响系统的稳定性。
为了更好地说明阻抗变化对电压的影响,文中假设:负序电流被抑制为0,且正序电流能迅速跟踪指令值;负序电压相对正序电压较小,暂不考虑功率波动对稳定性的影响;电阻相比于电感足够小,阻抗角接近于90°。
则式(4)、式(5)可以改写为:
(14)
(15)
进而求出有功功率P为:
(16)


图7 功角特性Fig.7 Characteristic of power-angle
阻抗参数变化时系统特征根轨迹如图8所示。图8(a)中,当Zg幅值|Zg|由3.31 Ω逐渐减小至1.32 Ω时,部分特征根会远离虚轴,但主导模态对应的特征根会靠近虚轴,说明发明单相接地故障时,|Zg|减小会削弱MMC系统的小信号稳定性。而当|Zg|减小至1.69 Ω时,会有一对特征根越过虚轴,使得系统失去稳定。图8(b)中,ZF幅值|ZF|由7.57 Ω逐渐增大至15.14 Ω时,主导模态对应的特征根逐渐靠近虚轴,导致MMC系统的小信号稳定性减弱。当|ZF|增大至13.18 Ω时,会有一对特征根进入不稳定区域。

图8 阻抗参数变化时系统根轨迹Fig.8 Root-locus with varying impedance
3.2 电流耦合对稳定性的影响
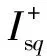

图9 正序电压相量图Fig.9 Phasor diagram of positive sequence voltage


图变化时系统根轨迹Fig.10 Root-locus with varying
4 仿真验证
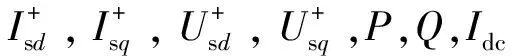
4.1 阻抗参数变化的稳定性验证

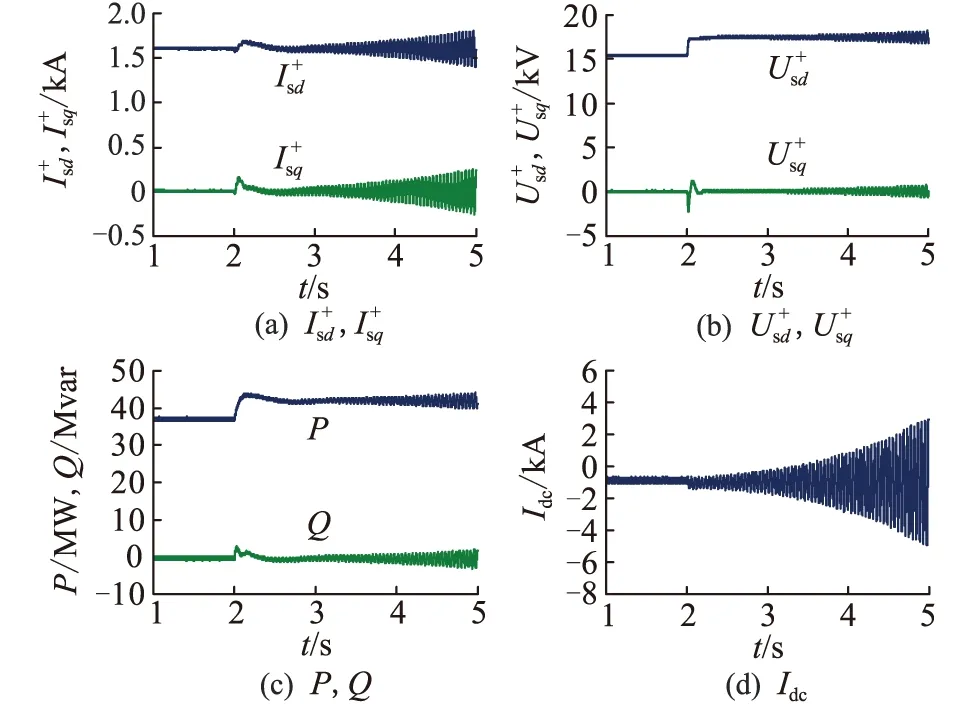
图11 |Zg|变化时的仿真验证Fig.11 Simulation validation with varying |Zg|
在2 s时,|ZF|由7.57 Ω增大至15.14 Ω,仿真结果如图12所示,此时系统出现了很明显的振荡失稳现象,验证了理论分析的正确性。
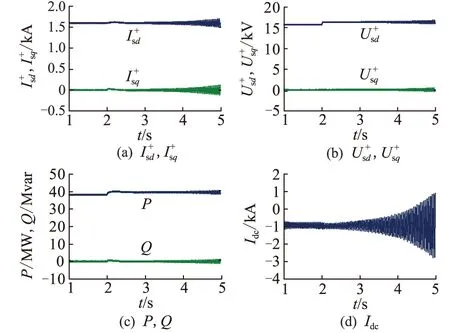
图12 |ZF|变化时的仿真验证Fig.12 Simulation validation with varying |ZF|
4.2 电流耦合的稳定性验证
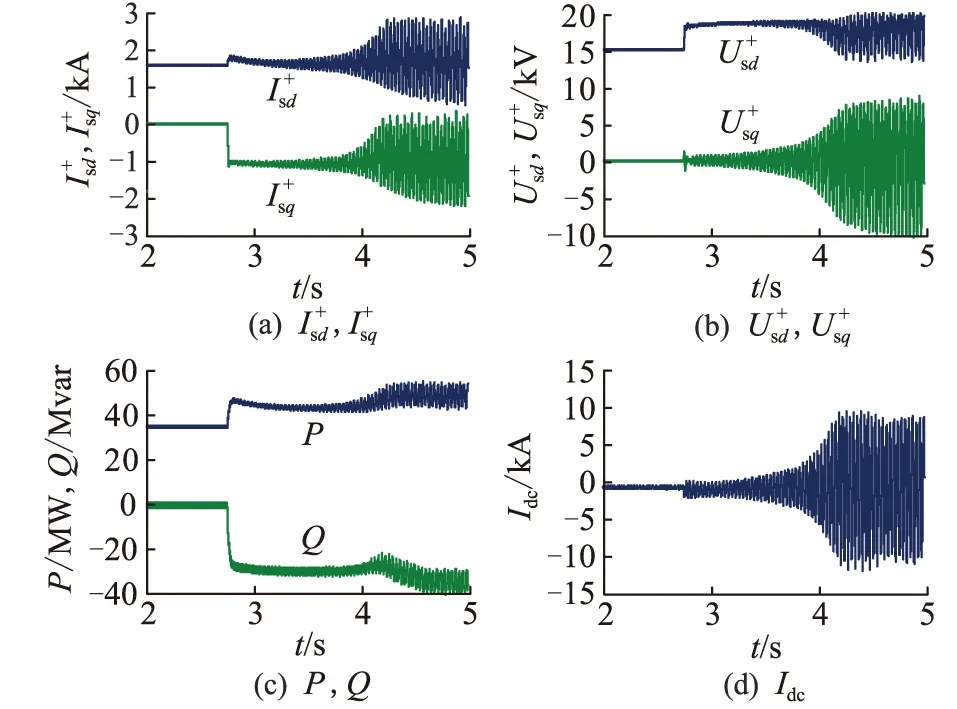
图13 仅注入的仿真验证Fig.13 Simulation validation with only

图14 混合注入和的仿真验证Fig.14 Simulation validation with mixed injection of
5 结论
文中首先建立了单相接地故障下考虑接地阻抗的MMC系统交流侧序网络模型,并给出了端电压表达式,然后与MMC及控制系统的状态方程联立并线性化得到MMC系统的小信号模型。对所得模型进行稳定性分析,其主要结论如下:
(1) 减小Zg或增大ZF,使有功功率增加的同时也会使电网电压与并网点电压之间的相角差减小,不利于MMC系统的稳定性。
