基于SSRCKF的纯角度和纯距离跟踪滤波器*
2021-08-12张星星刘乐文
张星星 刘乐文
(兰州理工大学电气工程与信息工程学院 兰州 730050)
1 引言
纯角度跟踪(Bearing-only Tracking,BOT)和纯距离跟踪(Range-only Tracking,ROT)在军事领域有着极为广泛的应用,如使用红外传感器等进行的电子作战、水底目标跟踪、空中目标监视等,因此近十几年来引起了许多学者的关注和研究。由于具有高度非线性和量测信息的不完整性,使得BOT和ROT在实际应用中具有较大的困难。结合扩展卡尔曼滤波(Extended Kalman Filtering,EKF)解决BOT和ROT问题是最基本和应用最广泛的方法[1~3]。EKF的实质是将非线性函数局部线性化,虽然处理方法简单,但由于高阶项的省略,当系统的非线性程度较强时其滤波的效果变差。进一步研究发现,相较于近似非线性函数而言,近似概率分布更加容易,即通过利用不同的采样策略进行多点采样逼近非线性分布,典型的有无迹卡尔曼滤波(Unscented kalman filtering,UKF),容积卡尔曼滤波(Cubature kalman filter,CKF)等[4~6]。UKF计算复杂度与EKF相同,但滤波精度高于EKF的同时不会受系统非线性强度的影响,然而UKF存在可能出现的协方差非正定、高维系统滤波精度降低等问题[7]。由此,针对高维非线性系统以及UKF协方差非正定的情况,提出了基于三阶球面—向径容积规则的容积卡尔曼滤波,其权值均为正解决了协方差不正定的问题,而且当系统状态维度大于三维时,CKF的滤波精度高于UKF,因而得到了广泛的应用[8~11]。
本文主要针对纯角度和纯距离跟踪模型的部分可观测性和高度非线性问题,在CKF的基础上研究了最新的滤波算法球面单纯形—径向容积卡尔曼滤波算法(Spherical simplex-radial cubature kalman filtering,SSRCKF)[12~14]。由于在高维非线性系统中,SSRCKF不仅滤波精度高于传统的CKF,而且相对高阶的CKF计算复杂度降低。所以本文主要结合SSRCKF解决纯角度和纯距离跟踪问题,提出了球面单纯形—径向容积卡尔曼纯角度和纯距离跟踪滤波器。将SSRCKF与纯角度跟踪和纯距离跟踪结合对提高BOT和ROT问题的滤波精度和降低其复杂性具有重要的实际应用意义。
2 球面单纯形—径向容积卡尔曼滤波
非线性高斯系统建模如下所示。
状态方程:
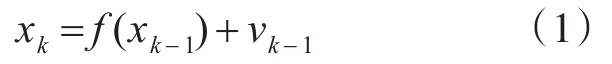
量测方程:

其中,xk∈Rn为系统状态向量,n为系统状态维度;zk∈Rm为量测向量,m为系统量测维度;f(·)和h(·)为非线性方程,vk和nk分别为系统噪声和量测噪声,两者互不相关且均为均值为零的高斯白噪声,方差分别为Qk和Rk。
根据文献[11]和[12]可得,高斯前提下贝叶斯滤波器递推过程中的多维向量积分可以统一表示为
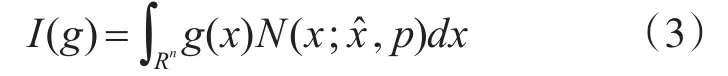
其中,g(x)表示任意非线性函数,N(x;,p)表示以x为变量,均值为,协方差为p的高斯分布。若令x=ry,则有xTx=r2yTy。其中,r≥0为球体的半径;Un={y∈Rn|yyT=1}表示单位球体的表面,y为方向矢量,σ(y)表示Un上的元素。式(3)可以转化为
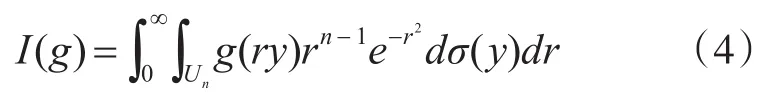
分解可得球面积分:
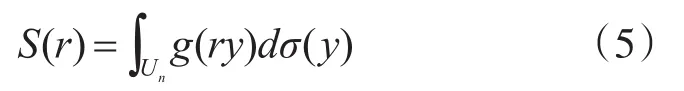
径向积分为
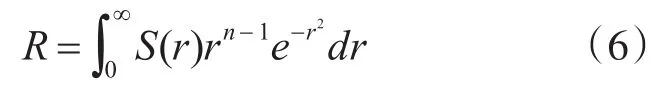
1)球面单纯形准则
球面单纯形准则是利用n-单纯形求解式(5)球面积分的一种方法。n-单纯形是指在n维及以上欧氏空间中的n+1个与仿射无关的点集凸包[12]。从几何角度可看作一个n维的几何体。若设n-单纯形的n+1个顶点构成的向量由ai=[ai,1,ai,2,...,ai,n]T表示,其中i=1,2,...,n+1。
则向量的各个构成元素定义为
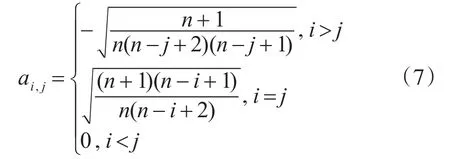
{ai}满足中心对称性,可选作积分点,再结合球面容积规则推导如下。
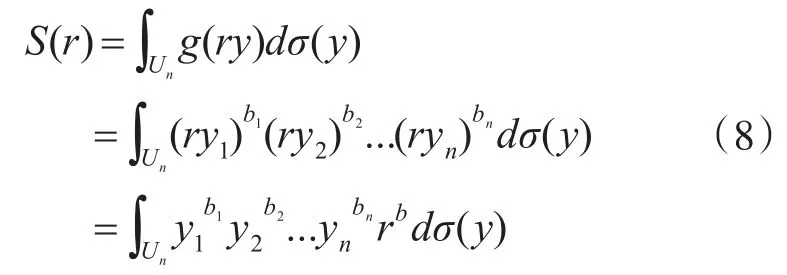
由单项式球面积分的闭式解原理[15]可得
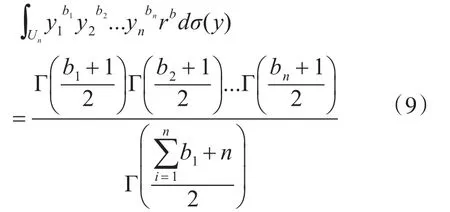
同时,球面积分可由数值积分近似

其中,yi和ws分别表示采样点及其对应的权值。由于采样点满足中心对称性,所以三阶单纯形球面准则只需考虑零阶单项式g(y)=1和二阶单项式g(y)=y12,分别代入式(8)可得

将式(14)代入式(12)得y2=1。
由此,2(n+1)个点的三阶球面单纯形准则可表示为
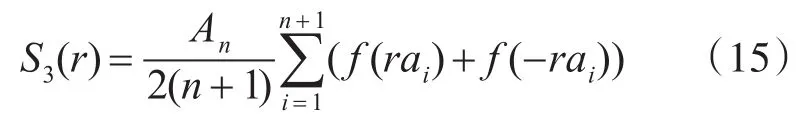
所以,球面积分的点球面单纯形准则可以推广为
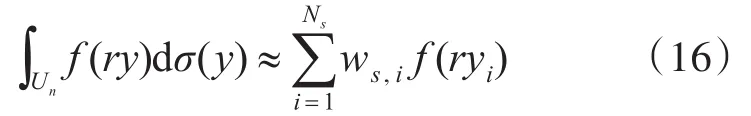
径向准则是一种借助数值积分求解球面积分的方法,即
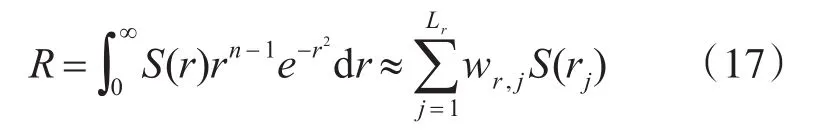
令S(r)=rl,则径向积分可以转换为
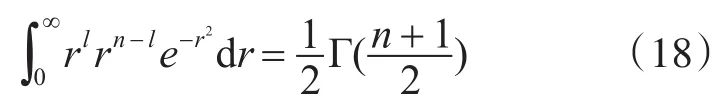
若球面-径向容积准则对应的积分点完全对称,那么径向积分只要满足偶数阶代数精度即可。通过不同的偶数阶单项式的匹配,可确定不同的点及其对应的权重[15~16]。
利用矩匹配法就可得到仅包含一个点的三阶径向准则,零阶矩方程和二阶矩方程分别为
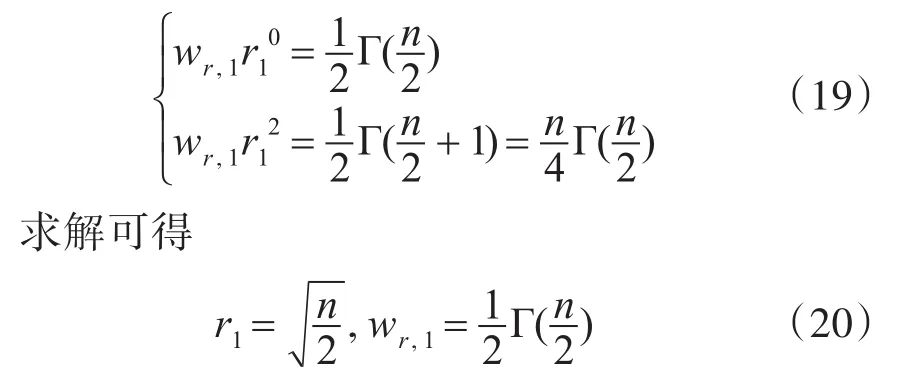
所以,三阶径向准则为
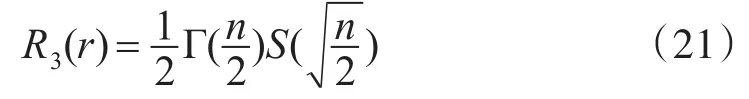
整理球面单纯形准则(16)和径向准则(17),再将式(15)和式(19)代入可得三阶单纯形球面径向容积规则(SSR):
嘉靖五年七月,费宏为少师兼太子太师吏部尚书华盖殿大学士,杨一清为少师兼太子太师吏部尚书谨身殿大学士。华盖殿大学士高于谨身殿大学士,故费宏地位高于杨一清。嘉靖二十四年十二月,夏言为少师兼太子太师吏部尚书华盖殿大学士,严嵩为少师兼太子太师吏部尚书谨身殿大学士。夏言取代严嵩成为首辅。
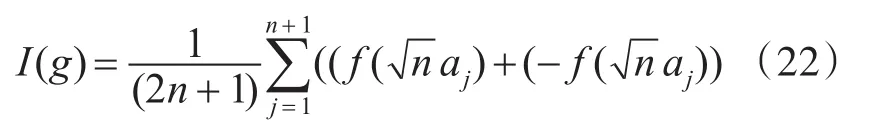
进一步,结合SSR与贝叶斯滤波框架,得到球面单纯形-径向容积卡尔曼滤波器。表1总结了CKF和SSRCKF采样点数与系统状态维度之间的关系。

表1 SR和SSR采样点数的比较
3 球面单纯形—径向容积卡尔曼纯角度跟踪和纯距离跟踪滤波器
纯角度跟踪是利用被传感器获得被跟踪目标的角度信息,但不能得到目标的距离信息,这种目标跟踪的结果具有唯一性[17~19]。
标系下建立目标纯角度跟踪系统的数学模型:状态方程与式(1)相同。
量测方程:
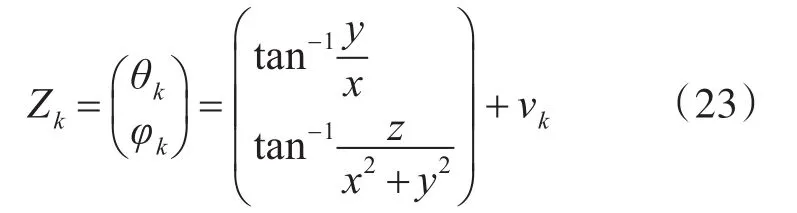
其中(x,y,z) 是目标的直角坐标,θk,φk分别表示雷达所测的方位角和高低角,系统噪声wk-1和量测噪声vk均为相互独立的零均值高斯白噪声。
根据式(23)确定球面单纯形—径向容积卡尔曼纯角度跟踪算法在k时刻的容积采样点及相应权值为
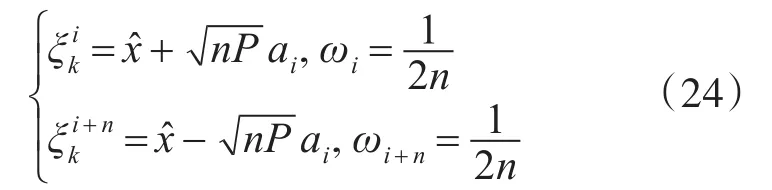
i=1,2,…,n,n为系统的状态维度,ai为由式(7)确定的n-单纯形的n+1个顶点构成的向量,和P分别为k-1时刻的后验均值和协方差。则具体的滤波算法如下。
预测:
采样点的预测和系统状态的预测分别为
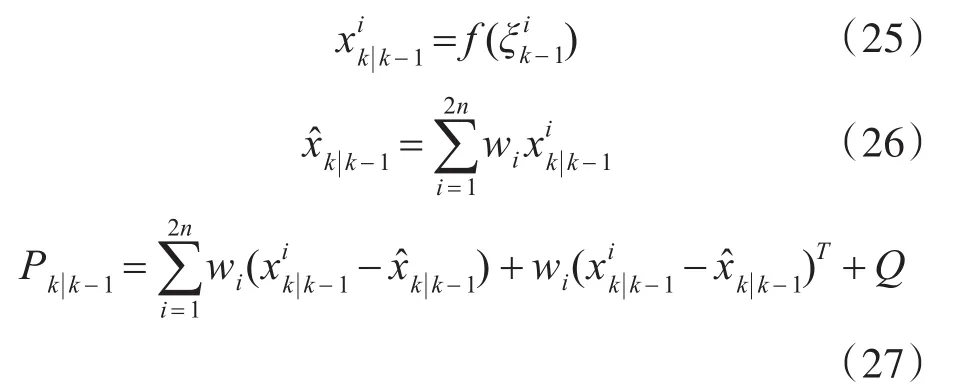
根据一步预测,再次利用三阶SSR产生新的容积点集。
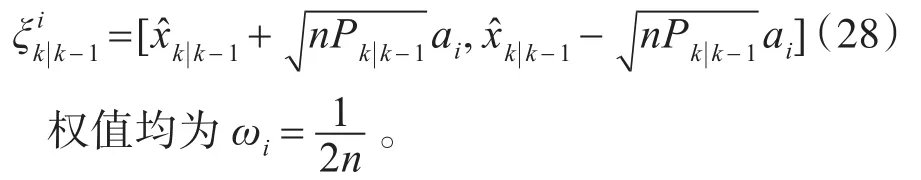
更新:
纯角度观测向量预测为

上述式(1)和式(23)~(35)构成了完整的球面单纯形—径向容积卡尔曼纯角度跟踪滤波算法。
在纯距离目标跟踪模型下,量测系统能获取的量测信息只有距离,相较于纯角度跟踪而言可观测程度更低,对滤波器的性能要更高[20],利用SSRCKF解决纯距离目标跟踪问题有更长远的意义。
在直角坐标系下建立目标纯角度跟踪系统的数学模型:状态方程与式(1)相同。
量测方程为
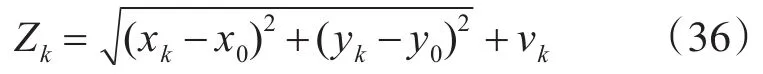
其中(x0,y0)和(xk,yk)分布为二维空间中观测雷达的位置和k时刻目标所在的位置。
由于在球面单纯形—径向容积卡尔曼纯角度跟踪算法的基础上,只要注意量测方程的预测和更新,球面单纯形—径向容积卡尔曼纯角度跟踪算法简单明了,这里不再进行详细的推导说明。
4 仿真分析
本部分主要给出两种不同场景下的仿真从而验证上文中提出滤波器的正确性。首先,比较二维系统中EKF纯距离跟踪、UKF纯距离跟踪、CKF纯距离跟踪、SSRCKF纯距离跟踪等不同滤波算法对CA运动目标的跟踪效果;其次,在三维系统中比较以上不同的滤波算法对CA运动目标的纯角度跟踪的效果。
4.1 球面单纯形—径向容积卡尔曼纯角度跟踪
仿真场景一:在三维空间中,目标运动模型为CA模型,扫描周期T=1s总的采样次数是100/T,用向量描述系统状态,其中x、y和z分别表示目标在x轴、y轴和z轴上的位置分量,、和分别表示目标在x轴、y轴和z轴上的速度分量,、和分别表示目标在x轴、y轴和z轴上的加速度分量,观测雷达的位置在原点,该雷达只能接收到目标的角度信息(即方位角和高低角),则运动目标在直角坐标系中的数学模型可以表示为
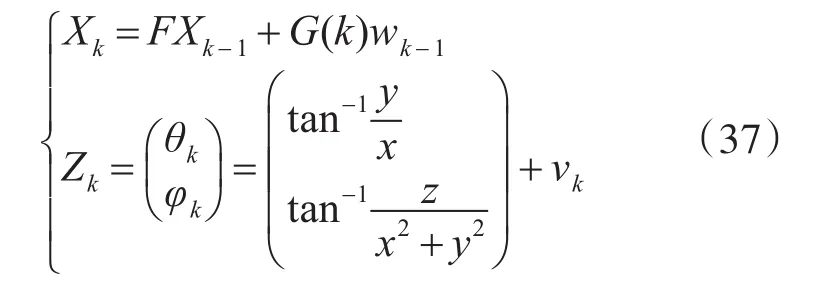
其中,系统噪声wk-1和量测噪声vk均为相互独立的零均值的高斯白噪声,其对应的方差分别为Qk=diag([0.01,0.02,0.02]T),Rk=diag([0.002,0.002]T),目标的初始状态设置为X0=[10,10,3,1000,10,-3,100,50,-5]T,G(k)为噪声驱动矩阵,F为状态转移矩阵。
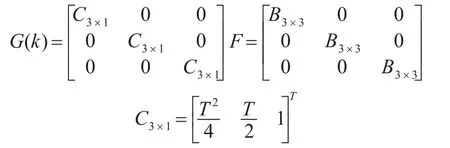
UKF算法中的参数设定分别为系统状态维度L=9,自由调节参数k=0,控制采样点的分布状态α=1,非负权系数β=2,缩放比例参数λ=3-L。
在该仿真场景下分别对非线性滤波算法EKF、UKF、CKF以及SSRCKF进行仿真实验比较,仿真过程中,误差分析公式为

其中,xij和ijk分别表示xi和i第j次采样值。
图1给出了该仿真场景下目标的实际运动轨迹以及分别采用EKF、UKF、CKF、SSRCKF四种纯角度滤波算法得到的目标运动轨迹。图2为该场景四种算法滤波后得到的目标位置的误差分析曲线。结合图1和图2,可以很明显地看出在三维空间对目标的纯角度跟踪中球面单纯形—径向容积卡尔曼纯角度跟踪具有很大的优势。由于EKF的局部线性化,不适用与强非线性系统,所以EKF纯角度滤波器发散,其滤波效果最差。相较于EKF纯角度滤波器而言,UKF纯角度滤波器的滤波精度收敛,但由于UKF在高维系统(此时的系统维度为n=9)中滤波精度会下降,所以UKF纯角度滤波器的误差曲线在CKF纯角度滤波器之上,这证明了CKF在高维非线性系统的优势。误差最小的算法是本文提出的SSRCKF纯角度滤波算法,且此时估计轨迹与真实轨迹几乎重合,这就验证了在系统状态维度更高,非线性更强的系统,该滤波器较其他纯角度滤波器在滤波精度上具有更大的优势,同时更进一步说明了SSRCKF算法的优越性。
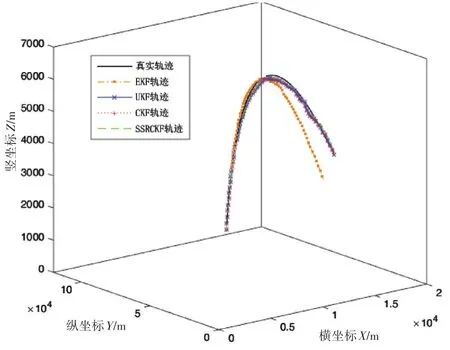
图1 场景一中目标的真实轨迹与滤波轨迹
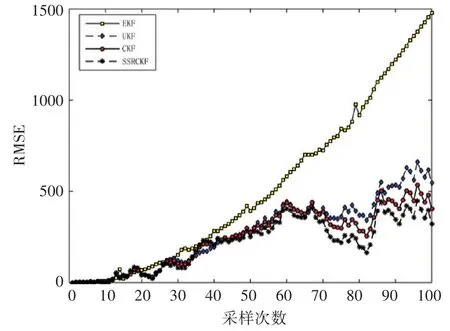
图2 场景一中目标位置的误差分析曲线
另一方面,由于此时系统维度n=9,由表1可知当n≥7时,SSRCKF的采样点会少于CKF,且n越大,两者采样点个数相差越大,由此,SSRCKF纯角度滤波器的计算复杂度得到了有效的降低。
4.2 球面单纯形—径向容积卡尔曼纯距离跟踪
仿真场景二:在二维空间中,选择CA模型作为目标运动模型,扫描周期T=1s总的采样次数是60/T,用向量描述系统状态,其中x和y分别表示目标在x轴和y轴上的位置分量,和分别表示目标在x轴和y轴上的速度分量,和分别表示目标在x轴和y轴上的加速度分量,假设观测雷达的位置为x0=200,y0=300,该雷达只能接收到目标的距离信息,则运动目标在直角坐标系中的数学模型可以表示为
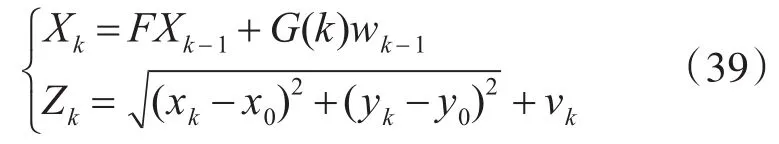
其中,系统噪声wk-1和量测噪声vk均为相互独立的零均值高斯白噪声,其对应的方差分别为Qk=diag([0.001,0.001]T),Rk=0.01,目标的初始状态为,噪声驱动矩阵G(k)和状态转移矩阵F分别为
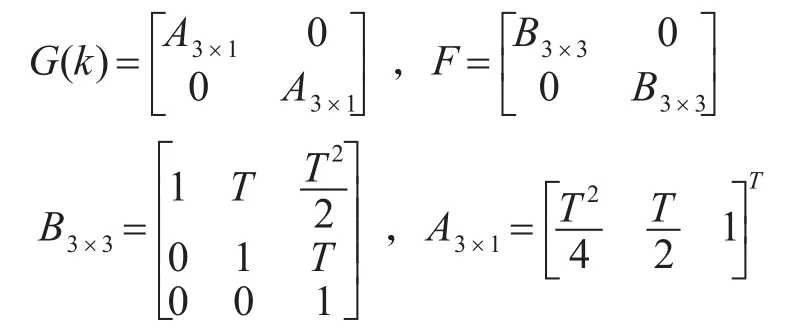
其中,UKF算法中的参数设定为系统状态维度L=6,自由调节参数k=0,控制采样点的分布状态α=1,非负权系数β=2,缩放比例参数λ=3-L。
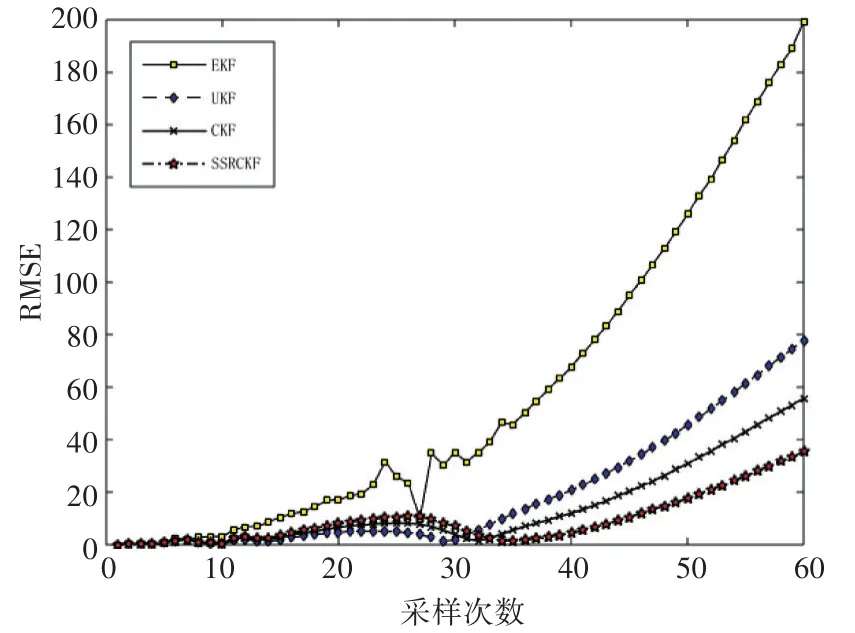
图3给出的是场景二下的目标的实际运动轨迹以及分别采用EKF纯距离跟踪、UKF纯距离跟踪、CKF纯距离跟踪、SSRCKF纯距离跟踪四种算法得到的目标运动轨迹。图4为场景二中四种算法的目标位置误差分析曲线。
观察和分析图3和图4可得,在高维非线性系统中(n=6),几种非线性纯距离跟踪算法的滤波性能的排序为EKF 图3 场景二中的目标真实轨迹与滤波轨迹 图4 场景二中目标位置的误差分析曲线 综合以上两个仿真,在系统状态维度更高,非线性更强的系统中相对于其他的非线性纯角度滤波器和纯距离滤波器而言,SSRCKF纯角度滤波器和SSRCKF纯距离滤波器不仅滤波精度更高,估计误差更小,而且计算复杂度更低,效率更好。但另一方面,纯角度和纯距离滤波器存在的一旦系统状态发生突变就无法精确跟踪的问题和进一步减少计算量的目标也将是未来研究工作的重心所在。 本文针对纯角度跟踪和纯距离跟踪所具有的部分可观测性和高度非线性,结合SSRCKF提出了球面单纯形—径向容积卡尔曼纯角度和纯距离跟踪滤波器,并在高维非线性系统中与其他非线性纯角度和纯距离跟踪滤波器进行了比较,验证了所提算法的优越性。仿真结果表明,该算法在提高滤波精度的同时还减少了计算量,这一点在只能获取不完全状态信息的军事领域具有重要的理论意义和应用前景。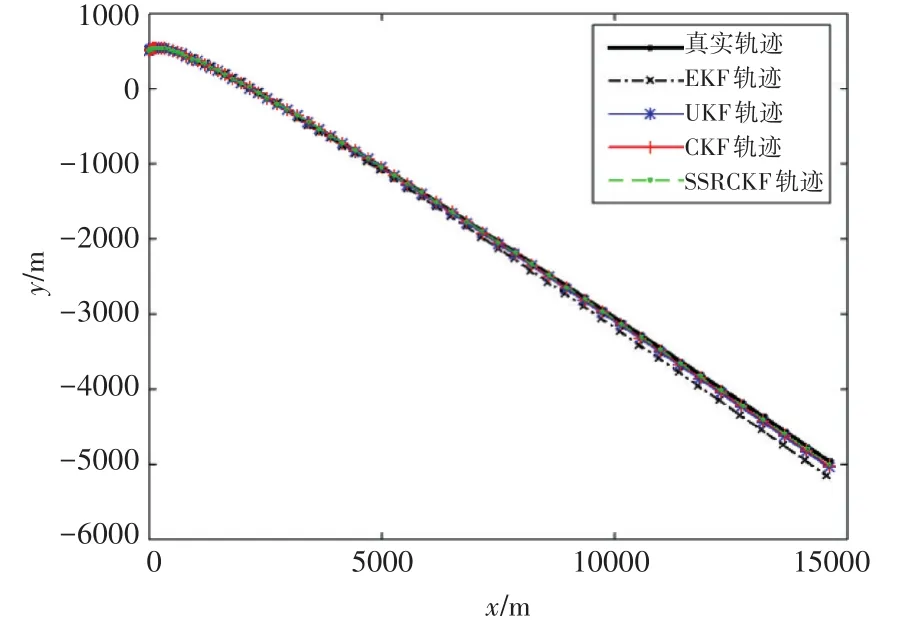
5 结语
