旋转干涉仪定位体制系统误差标校方法

苏成晓，郭 辉，徐海源，吉 宇，翟宏骏，方 猛

（1.北京遥感信息研究所，北京 100011；2.中国航天科工集团8511研究所，江苏 南京 210007）

0 引言

旋转基线定位过程中，除了信号噪声带来的相位差随机误差，干涉仪基线的2个接收通道幅/相不一致性、环境温度的变化等因素，都将导致相位差测量存在系统误差[1-2]。基线长度、方位安装角、俯仰安装角和转台转角，受测量水平的限制会产生天线位置系统误差；地面测试环境和真实的应用场景（如星载场景）存在一定的差异，因此无法直接测量出这些系统误差。旋转基线由于器件结构的非均匀、物理磨损等原因也会引入一定的系统误差，如旋转基线在旋转过程中，旋转面和基准面存在较小的倾角。另外，在定位过程中需要的观测量还包括辐射源信号频率、观测站位置、姿态等，这些观测量均可能产生一定的系统误差[3]。

本文针对旋转干涉仪定位体制中系统误差的标校问题进行探讨，通过分析其可等效为转角偏差、倾角偏差、横滚角偏差和通道偏差四个校正量的影响，利用迭代最小二乘参数估计算法，给出标校量的精确估计，进一步提升系统的定位性能。

1 旋转干涉仪相位差模型

基线旋转过程中，在获得相位差测量值后，可利用相位差与目标位置的关系，解算出目标位置。旋转干涉仪定位示意图如图1所示[4]。

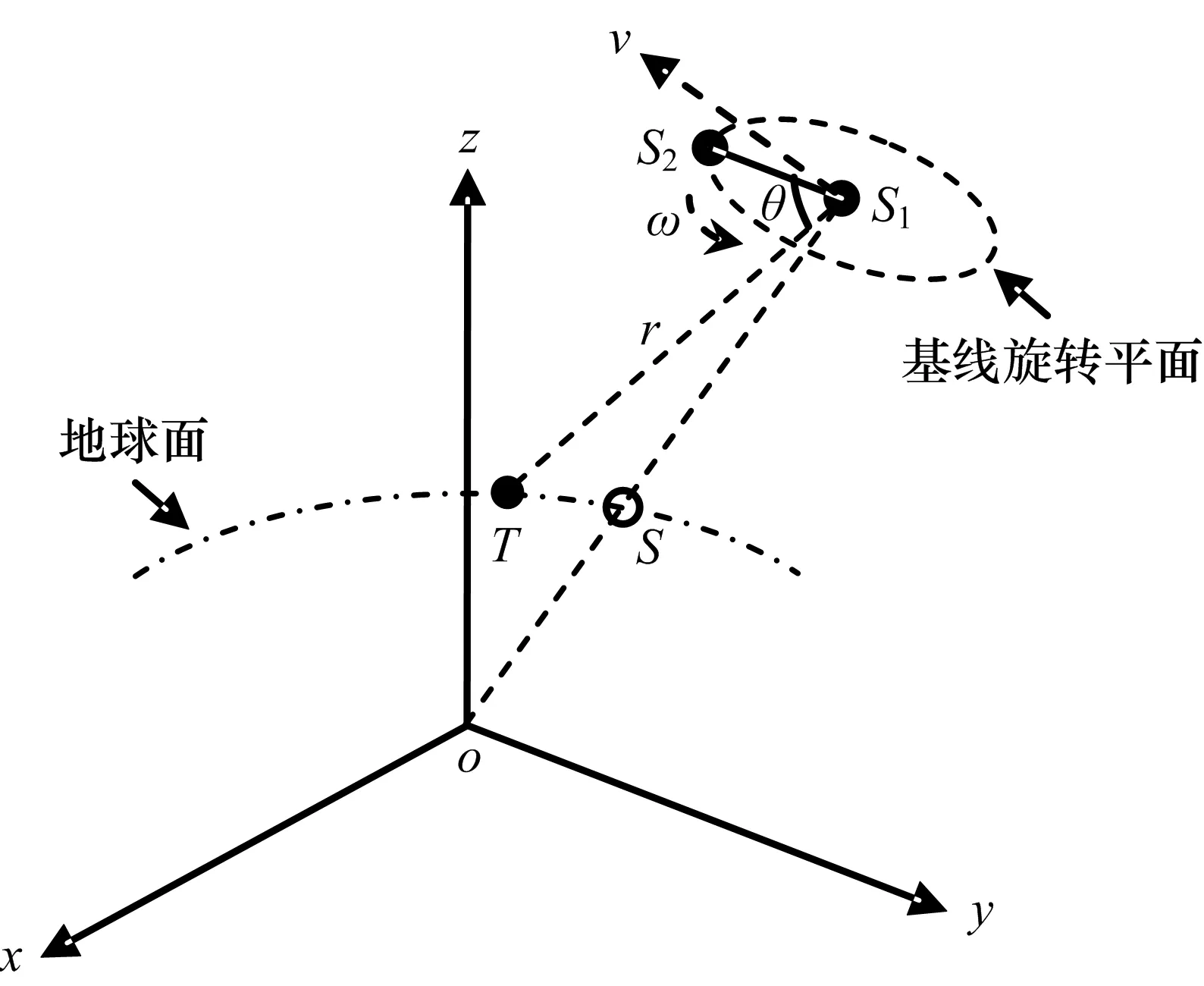
图1 旋转干涉仪定位示意图

1.1 理论相位差

卫星在轨运行过程中，侦收到的第n个脉冲的相位差可表示为[5]：

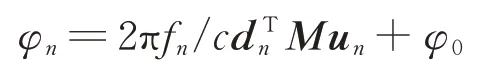
式中，fn为信号频率，d n＝d[cosθn,sinθn,0]T为基线旋转矢量，即向量S1S2，d为基线长度，M为WGS84坐标系到卫星本体坐标的转换矩阵，u n＝[x n,y n,zn]T为位置单位矢量，即向量S1T，φ0为初相。

1.2 相位差系统误差

将通道幅/相不一致、载荷与转台时间不同步、基线旋转平面与卫星平台本体非共面等因素引入的相位差系统误差，等效为转角偏差bθ、倾角偏差bγ、横滚偏差bη和通道偏差bφ4个校正量的影响，重新定义基线旋转矢量为：

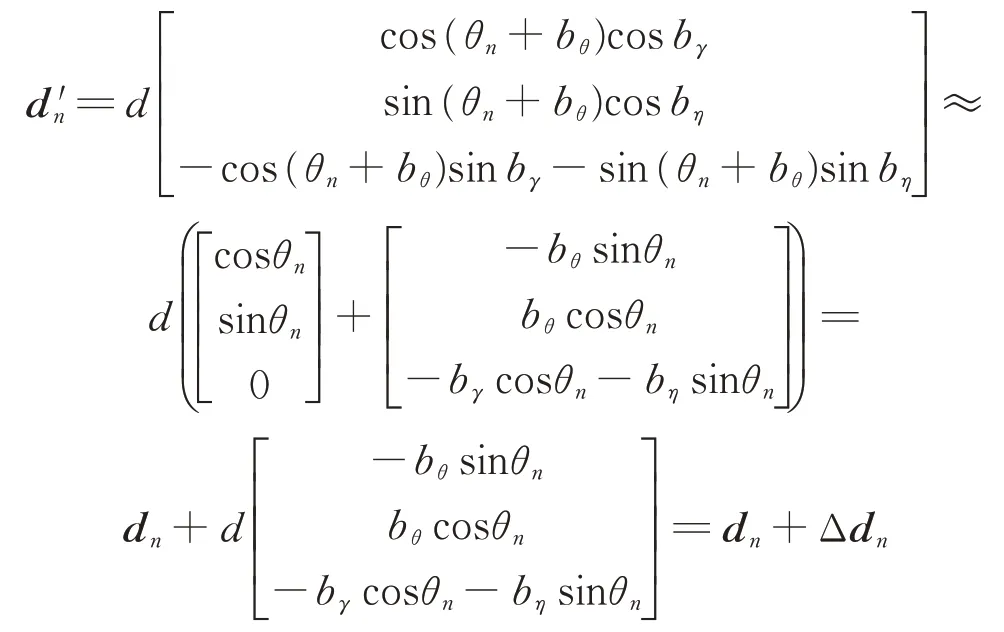
进一步可得校正后的相位差为：

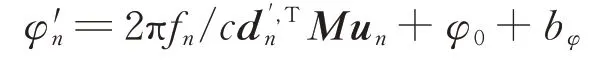
相位差系统误差可表示为：

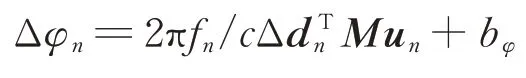
2 迭代最小二乘校正方法

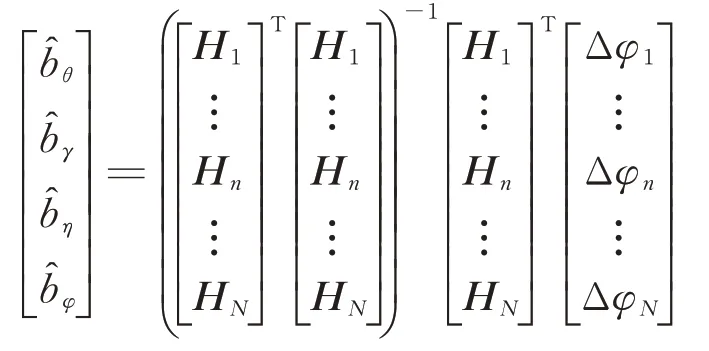
根据上述分析可知，相位差系统误差可进一步表示为：

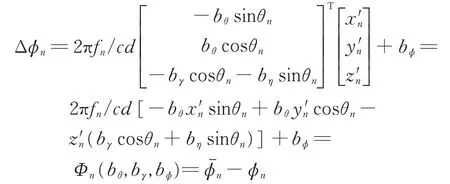
式中，为第n个脉冲的相位差测量值，[x′n,y′n,z′n]T为卫星本体坐标系下的位置单位矢量。基线旋转过程中，累积N次相位差测量数据，可利用非线性最小二乘算法，获得bθ、bγ、bη、bϕ的近似估计，即：

式中，

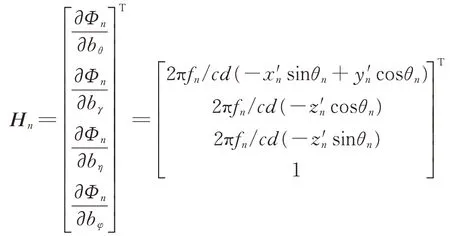
由于进行了线性化处理，采用的估计算法可近似认为是无偏估计，但与真实值仍存在较小的误差，尤其当目标离星下点较远时，较小的误差将会导致较大的定位误差，因此需要进一步提高参数估计的精度。本文将估计获得的转角偏差、倾角偏差、横滚偏差和通道偏差代入校正后的相位差表达式，重新获得测量相位差和校正后相位差相减后的相位差系统误差：

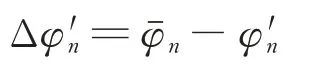
同样采用上述非线性最小二乘算法，获得第1次迭代估计后的转角偏差Δ(1)、倾角偏差Δ(1)、横滚偏差Δ(1)和通道偏差Δ(1)，循环迭代K次后，可得转角偏差、倾角偏差、横滚偏差和通道偏差4个校正量的最终估计值为：

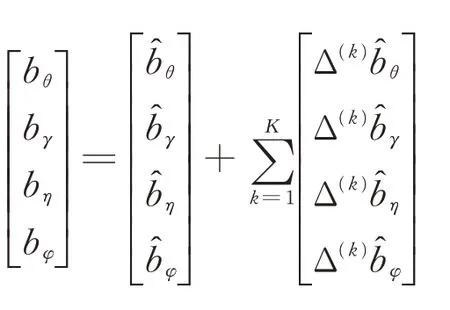
3 仿真分析

设置标校源信号频率为6 GHz，信号入射俯仰角为54°，目标位置经纬度为（136.084 5o，26.645 2o），采集一段时间的相位差数据，根据卫星星历、转台转角、目标位置，反推理论相位差，与测量相位差的差异如图2（a）所示，利用本文迭代最小二乘算法估计出转角偏差、倾角偏差和通道偏差后，再次反推校正后相位差，与测量相位差的差异如图2（b）所示，可以看出，本文提出的校正方法能够较好地完成系统误差的标校。

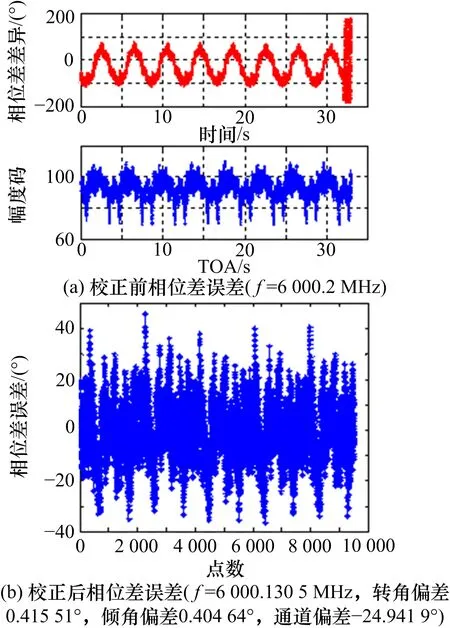
图2 系统误差校正效果图

另外，对比采用最小二乘估计算法和迭代最小二乘估计算法进行校正后的定位效果，如图3所示，可以看出基于迭代最小二乘标校后的定位结果分布在真实位置附近，可以近似为无偏估计，进一步提升了系统的定位精度。

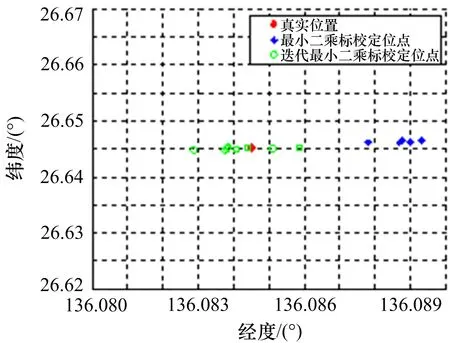
图3 迭代最小二乘标校定位效果图

4 结束语

针对旋转干涉仪定位体制中系统误差的标校问题，本文提出一种迭代最小二乘估计算法，通过多次迭代处理，可获得转角偏差、倾角偏差和通道偏差的精确估计，从而进一步提升系统的定位性能。该方法能够较好地克服相位差系统误差对定位结果的影响，对旋转干涉仪体制的实际应用具有比较重要的参考价值。■