可变附着系数路面上的自动紧急制动避撞安全策略研究*

2021-08-12兰凤崇刘迎节陈吉清蓝庆生

汽车工程 2021年7期

兰凤崇，刘迎节，陈吉清，蓝庆生

（1.华南理工大学机械与汽车工程学院，广州 510640；2.华南理工大学，广东省汽车工程重点实验室，广州 510640）

前言

车辆面临碰撞风险时，驾驶员可能出现制动不及时的情况，采用自动紧急制动（autonomous emergency braking，AEB）系统主动介入制动过程可有效提高行车安全［1］。当前的AEB系统多采用安全距离或安全时间模型，通过预判车辆与障碍物相对位置的变化趋势，评估车辆的碰撞风险等级并采取对应策略实现可靠的避撞控制［2］。采用单一的安全模型可以带来简洁而高效的决策过程，但也存在无法全面兼顾各类安全风险的缺陷，因此有学者将不同形式的安全模型进行联合以强化安全性能。例如，Dong等［3］将基于行车间距保持等原理的安全模型加权耦合为多重安全距离模型参与制动决策，在提高车辆安全性的同时减少了换道过程制动系统的误触发。Chen等［4］建立了同时考虑碰撞时间与制动距离的避撞策略，通过两类安全模型的冗余校核提高了预警系统的可靠性。

车辆行驶过程具备很强的动态变动特性，道路条件的变化又将改变车辆的制动效果，车辆安全状态的准确评估离不开对路面状态的实时辨识和据此对复杂动态变化车辆运动位置的预测［5］。因此，一些研究致力于探索道路工况信息的准确辨识方式，如Zong等［6］采用双重扩展卡尔曼滤波器实现了对道路附着系数的估计，并在几类典型工况下验证了结果的准确性。付翔等［7］通过记忆衰减机制降低了模型不准确带来的滤波误差，基于无迹卡尔曼滤波实现了对路面附着系数的精准辨识。Qi等［8］借助车辆自带传感器的偏航、轮速等信息，基于无迹卡尔曼滤波实现了低传感器成本的路面附着系数估计。另一些研究则着重提升复杂多道路场景下的车辆综合避障性能，如Koskinen等［9］通过辨识所得的极限附着系数来修正制动的触发时机，提高了湿滑工况下紧急制动系统对路面附着力的利用率。汪龚等［10］则根据道路附着能力，结合车辆碰撞危险等级，确定所应采取的制动强度，实现了兼顾安全与乘员舒适性的避撞控制。Han等［11］根据峰值附着系数估计结果计算并更新制动时间阈值，实现了可适应不同道路条件紧急制动控制。Kim等［12］基于道路坡度和附着条件，采用前馈控制器修正最小制动距离，消减了实际道路工况变化对制动过程的影响。周兵等［13］同时考虑动态路面环境与测量噪声，通过模糊算法获取车辆减速性能并预测其运动形式，提高了碰撞危险评估结果的准确性。

多数紧急制动策略未考虑车辆加速度，特别是在车辆行驶速度存在快速大幅变动的情况下，这不利于实现对车辆运动位置的准确预判。而针对不同的行车场景，多数决策算法通过直接修正制动距离或时间以适应道路环境，存在避撞效果不稳定、精度波动大的问题，此时，精准辨识道路条件并充分解析实际的车辆性能-道路条件关系显得十分必要。此外，通过直接联合不同形式安全模型强化控制系统容错与安全性能的方式，其控制稳定性不佳。因此，为保证决策算法稳定与简洁，并减少制动系统的非必要触发，提高动态实时安全性，将加速度融入到制动决策规则中，按照前车加速度状态对制动工况进行细化，联合同一模型的多种校核条件建立动态决策增强安全时间模型；为提高决策算法对复杂变动道路场景的适应性，采用具备连续辨识能力的UKF算法精确估计路面附着系数，计算对应工况车辆可输出的极限减速度值，代入安全时间模型中更新安全校核条件，实时评估碰撞风险实现对制动时机合理可靠的决断，从而增强车辆在可变附着系数路面的安全性。

1 动态路面附着能力辨识方法

为增强控制策略对动态道路条件的适应性和安全性，作为表征路面条件的重要参数，附着系数是首先须准确获取的信息。建立整车全轮附着性与姿态动力学的关系模型，从而充分利用实时传感的车辆姿态信息，采用基于车辆动力学响应的估计策略实现对路面附着系数的连续精准辨识。

1.1 全轮整车动力学建模

基于动力学响应的路面附着系数估计依赖于完善的系统状态方程，轮胎作为与路面直接作用的车辆部件是反映道路信息的关键，为准确复现车辆在不同环境下的行驶特性，建立全轮整车动力学模型。构建坐标系统见图1，其中，X、Y、Z为大地坐标系，x、y、z和x'、y'、z'为车身和轮胎坐标系。定义车辆和轮胎坐标系与大地坐标系同向，原点分别为车辆和各轮胎的质心。

图1 坐标系统

为反映车辆运动过程的姿态响应特性，选取运动中主要涉及的纵向、侧向、横摆和侧倾4个自由度建立车身模型。

式中：F为车辆所受的力；Fz为整车垂直载荷；v为速度；下标1、2、3、4分别代表车辆左前、右前、左后及右后轮胎，下标x、y则表示各参数在相应方向的分量；m为整车质量；ms为簧载质量；hs为簧载质量质心高度；f为滚动阻力系数；CD为空气阻力系数；A为车辆迎风面积；g为重力加速度；ψ、φ分别为横摆角与侧倾角；a、b分别为前后轴到整车质心的距离；Kφ、Cφ分别为悬架系统的侧倾角刚度与侧倾阻尼系数；Ix为簧载质量侧倾转动惯量；Iz与Ixz分别为车辆横摆转动惯量和惯性积。

采用卡尔曼滤波的附着系数估计算法一般基于Dugoff轮胎模型，但该模型在极限摩擦工况附近的拟合效果不佳，故选取在拟合精度上具有优势的MF⁃Swift轮胎模型进行滤波探索。完整建立4个具备绕自身y'轴与z'轴旋转自由度的轮胎子系统，其输出的纵、侧向力为

式中：B、C、D、E分别为刚度、形状、峰值和曲率因子；SH和SV分别为水平和垂直偏置；SVy'κ为联合工况附加垂直偏置。

以δ为转向角度，引入轮胎力坐标换算公式：

通过式（3）和式（4）将轮胎坐标系下的轮胎力换算至车身坐标系，联合式（1）与式（2），得到完善的全轮整车动力学模型。

1.2 路面附着系数估计

首先对轮胎模型进行变换，假设轮胎在纵、侧向的摩擦因数相同，即

又因为

结合式（2）和式（6），将联合工况纵、侧向力表达式改写为关于附着系数μ的函数：

式中X为除附着系数外输入轮胎模型的当前状态参数。此处不对函数的具体表达形式进行展开，而是将模型直接封装成以附着系数与其余参数进行调用的模块，代入滤波过程进行运算。

针对车辆系统复杂性，采用非线性适应性较强的无迹卡尔曼滤波算法实现道路辨识。由于车辆状态方程中带有操纵输入，路面附着系数的状态方程及其观测方程可表示为

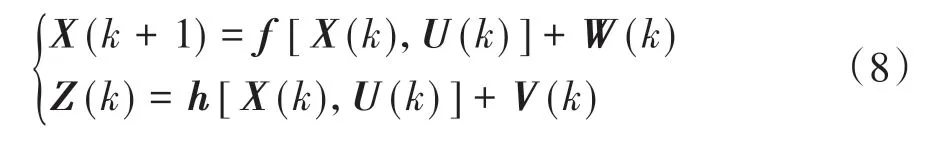
式中：f、h为状态与观测函数；W（t）、V（t）为过程与观测高斯白噪声，且分别具有方差Q和R。状态变量为X=［μ1，μ2，μ3，μ4］T，即4个车轮对应的路面附着系数；观测变量为Z=[ax，ay，ψ，φ]T，即不同路面附着系数下的车辆动力学响应参数；控制变量为U=［Fxi，Fy］iT，其中，i=1，2，3，4。

滤波过程的信息更新周期可小于0.02 s，路面附着系数在周期内产生的变化很小，因此其状态方程可以表示为

观测方程则由车辆动力学模型转化而来，根据式（1）和式（7）可得

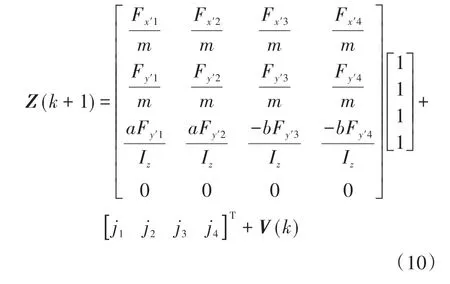
其中

在目标系统状态方程的基础上，进一步展开滤波操作，根据实时的车辆姿态参数观测值估计出路面附着系数。依据式（8）状态与观测方程，首先对轮胎横纵向摩擦因数的状态估计与误差的协方差进行初始化操作，即

接着，进行无迹变换，获取Sigama点集。

式中下标m、c分别表示均值和协方差，非负权系数β=3。接着，计算（2n+1）个Sigma点的一步预测。

然后，计算系统状态量的一步预测和协方差：

其次，根据一步预测的结果再一次使用式（13）生成新的Sigma点集X(i)(k+1|k)，其中，i=0，1，…，2n。同样通过式（14）计算对应权值，再次将预测所得Sigma点代入观测方程得到预期观测值：

随后，由观测值加权求和得到系统预测的均值和协方差：

进一步，计算卡尔曼增益：

最后，计算系统的状态更新和协方差更新为

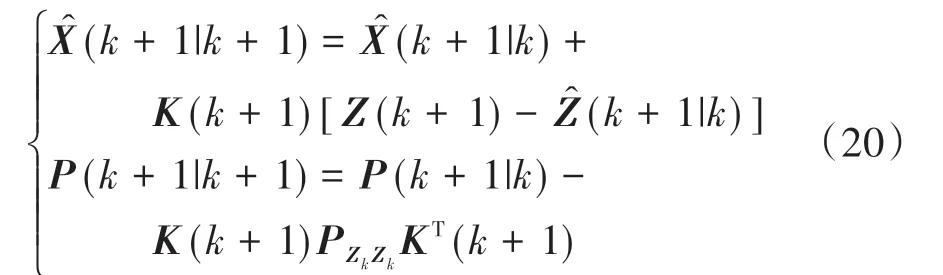
基于以上流程，不断进行迭代更新，实现对路面附着系数精准连续的最优估计。

2 可变路面附着下动态决策安全模型的紧急避撞

不同路面的附着能力有所不同，在可变路面附着性的道路条件下，紧急制动的最佳作用时机实时变化，且传统的安全距离避撞策略忽视真实道路条件所能提供的附着能力，默认所有道路的路面附着性一致，易造成自动紧急制动系统在可变附着性路面上避撞能力不足、避撞效率低等问题。为此建立目标车辆速度与加速度复合的动态决策增强安全模型，通过目标车辆的加速度变化对自车实现动态避障决策，同时考虑道路的附着性变化对车辆实际极限减速度能力的影响，增强车辆在制动避撞下的安全性。分析主车（即试验车辆）在不同目标工况下的紧急制动安全时间，结合车辆加速度状态进行动态安全校核。根据路面附着系数估计结果实时更新模型中反映路况的特征参数，从而增强控制策略对动态道路条件和车辆运动状态的适应性。

2.1 动态决策增强安全模型的制动避撞策略

为减少紧急制动系统的非必要触发，以目标车辆的加减速情况划分决策域，分别计算安全模型在不同执行目标下的安全时间，建立不同车辆运动状态下更具针对性的动态决策安全时间模型。将目标车辆的移动速度和相应的加速度初始值标记为vx1(0)与vx1(0)，试验车辆的运动速度和加速度初始值则记为vx0(0)与vx0(0)，两车的行驶过程的参数示意如图2所示。其中，d0、d1表示试验车辆与目标车辆的行驶距离，D则为两车间距，括号内参数为时刻。

图2 车辆行驶过程参数

根据车辆当前的速度与加速度，对其在一段时间后增加的行驶距离进行预测。假设制动器的延迟时间为ta，车辆在当前路况下可达到的实际极限减速度为vxbmax，则在时间（tt≥ta）内试验车采取制动措施后的行驶距离预测值为

目标车辆的行驶距离预测值为

设两车初始状态相距D（0）（D（0）＞0），则在t时刻两车相距为

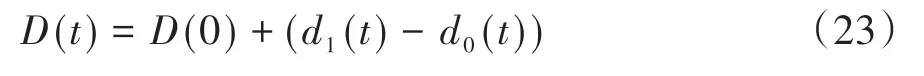
将式（21）和式（22）代入式（23）得

建立针对目标车减速工况的1号场景决策域，定义安全时间为试验车辆从触发制动到完全停止经过的时间为

建立针对目标车辆加速或匀速工况的2号场景决策域，定义安全时间为试验车从触发制动到与目标车等速时经过的时间tbc。由于

提出tbc得

定义极限车距Ds为两车行驶过程中允许出现的最小车距，则动态决策域避撞过程可描述为

也即在目标车辆加速或匀速行驶的情况下，判断试验车辆制动至与目标车辆等速时的两车间距是否大于等于极限车距；在目标车辆减速情况下，则判断试验车辆制动至完全停止时的两车间距是否大于等于极限车距。如果条件满足则不进行制动。否则，触发紧急制动。该设置可减少目标车加速工况下的非必要制动，且当目标车辆的速度恒为0时得到D（tb）s=D（tbc），算法依旧可以进行合理的紧急制动决策。

2.2 变附着性动态路况极限制动能力的试验辨识

考虑到实际路面工况在极限附着能力上存在的差异，以实际可达的极限减速度值作为安全模型中表征路况的特征参数，通过试验建立道路条件与车辆减速能力关系，根据路面附着系数估计值动态更新安全模型，确保算法可适应不同的道路条件。根据式（1），忽略车辆左右侧轮胎在动力学响应上的差异，并对轮胎纵、侧向力变换坐标系得到车辆纵向动力学公式为

在典型路面附着系数工况下测量车辆轮胎系统能够提供的最大纵向合力，并通过式（29），忽略风阻，计算得到不同路面的理论纵向减速度极限值，结果如表1所示，增设1和增设2为添加的两种不同路面附着系数的路面类型。

表1 典型路面附着系数下车辆系统特性参数

在实际制动过程中，轮胎并非完全处在输出峰值纵向力的极限状态，因此实际工作过程中可提供的极限减速度绝对值将有所降低。可设峰值制动力系数为λ（x0≤λx≤1），也即进行紧急制动时能够发挥出轮胎全部制动力的λx倍。选取具有代表性的小型SUV车型，搭载北斗星通的Npos320组合导航定位系统，通过其内置的陀螺仪动态测量并记录车辆的位姿信息，选择干燥沥青路面进行实车极限加减速工况试验，试验车辆如图3所示。

图3 试验车辆和传感器布局

记录的车辆纵向速度和加速度变化如图4所示。试验中车辆加速到接近20 m/s进行紧急制动，制动过程ABS系统介入工作，表明制动提供的减速度接近极限值。

图4 实车极限加减速工况试验

达到的极限减速度vxbtmax=-6.85m/s2，对应的理论减速度极限值vxbdmax=-7.24 m/s2，则峰值制动力系数为

实际制动过程制动力存在波动，不易达到极限减速的状态，取λx=0.92，则实际可达极限减速度为

取Ds=0.5 m，ta=0.3 s，采用样条曲线拟合实际可达极限减速度与路面附着系数之间的关系，根据输入的路面附着系数判断当前能提供的实际极限减速度值，代入安全时间模型中完成工况自适应更新，当动态计算结果不满足式（28）安全条件时即触发紧急制动。

3 多工况试验验证

在不同路面工况下，对路面附着系数估计算法和紧急制动策略的性能进行试验验证。

3.1 路面附着系数估计算法验证

在Simulink的S函数中介入车辆系统状态方程和UKF算法，通过其离散系统子函数实现UKF的周期性状态和时间迭代更新。对车辆模型输入外部控制参数和4个车轮对应的带噪声地面附着系数，获取车辆状态参数融入测量噪声，并与控制参数一同输入UKF开展滤波试验，得到试验平台如图5所示。其中，Simulink的S函数以仿真步长为更新周期进行迭代滤波计算，本试验设置仿真步长为0.01 s。控制量u通过轮胎模型计算出滤波过程的实际控制量U=［Fxi Fy］iT，并将车辆状态参数的积分扩展值也代入滤波方程中进行计算，以便通过车辆系统状态方程获取新的状态值。

图5 UKF路面附着系数估计试验

考虑路面条件变化的行车情形，进而以一段连续变化的附着系数进行仿真，结果如图6所示。

图6 变化路面附着系数工况辨识结果

在附着系数以复杂形式变化的情况下，估计结果实现了对实际值的良好跟随。在仿真的初始阶段，估计值快速收敛到真实值。在接下来的附着系数连续变化工况中，估计值则始终贴合真实值进行变化，且在低附着系数工况下未出现发散。而在附着系数阶跃回初始值时，估计值以小的超调量和比初始收敛过程更短的时间迅速跟随至实际值附近而完成收敛。试验结果表明，在连续变化的路面附着条件下，所搭建的辨识算法可有效实现对路面附着系数的估计，且具备良好的辨识精度和稳健的连续估计能力。

3.2 动态决策增强安全模式下紧急制动策略验证

接下来对紧急制动策略展开验证，为确保验证结果的可靠性，采用C⁃NCAP中针对AEB的测试标准进行验证。定义VUT（vehicle under test）为试验车辆，TV（target vehicle）为目标车辆，取C⁃NCAP测试工况如下：（1）CCRs工况：TV静止，VUT分别以20、30和40 km/h的速度在其后方行驶。（2）CCRm工况：TV以20 km/h的速度保存匀速行驶，VUT分别以30、45和65 km/h的速度在其后方行驶。（3）CCRb工况：VUT和TV均以50 km/h的初始速度行驶，初始车距分别为12和40 m，测试过程中TV在1 s内将减速度达到-4 m/s2进行减速运动，并保持至结束。由于在CCRs、CCRm工况中C⁃NCAP未指定初始距离，取车辆的初始距离为30 m。工况覆盖了车辆不同的速度与加速度组合形式，具备全面的验证效果。首先设置干燥沥青路面（μ=0.800），分别在3类测试工况的不同车速条件下对AEB系统进行试验，将3类工况试验过程各自出现的最危险结果记录下来，如图7所示。其中，蓝色虚线和橙色实线分别代表目标车辆和试验车辆随试验时间推进而行驶的距离，绿色点划线代表两车之间的距离。

图7 干燥沥青路面3类工况各自的最危险试验结果

自动紧急制动策略在不同测试工况与车速条件的组合工况下均有效实现避撞控制。在CCRs工况中，随着试验车辆行驶速度的增加，制动动作的激发时间不断前移，两车间的最小距离出现在试验车辆以20 km/h行驶的工况下，为0.84 m，大于设置的极限车距。在CCRm与CCRb工况中，最小车距则分别出现在TV以30 km/h行驶工况及两车初始距离为12 m的工况，为0.58与2.45 m，同样均大于极限车距。试验证明在干燥沥青路面工况下，紧急制动算法的应用可避免试验车辆与目标车辆发生碰撞，有效提高车辆安全性。

接下来设置不同的路面条件展开试验，对C⁃NCAP进行适当修改，不考虑C⁃NCAP中对路面附着系数的要求，设置除干燥沥青路面外最为常见的潮湿沥青路面（μ=0.563），开展避撞性能试验，同样给出3类工况各自试验所得最危险结果，如图8所示。

图8 潮湿沥青路面3类工况各自的最危险试验结果

图8显示良好的避撞效果，与干燥沥青路面工况的试验相比，湿沥青工况下算法制动触发时刻有所提前。这是由于湿沥青路面下的路面附着系数有所降低，试验车辆从制动触发到完全停止或与目标车辆匀速的时间较长，算法根据输入的路面附着系数值对制动触发的判断规则进行了修正，使控制算法得以适应路面情况的变化。各工况下两车在行驶过程中的最小距离比高附着系数路面均有所增加，也即随着附着系数的降低，算法的实际作用机制将向安全侧靠拢，这一特性有利于实际应用过程的行车安全。在3类工况的试验中，两车出现最小距离的工况分布情况与干燥沥青路面一致，最小距离分别为0.98、0.58和3.97 m，同样均大于设置的极限距离。试验证明，该算法在不同路面附着系数工况的各类复杂工况下，皆可有效实现对车辆的避撞控制。