复杂飞行任务人工磁场路径规划算法
2021-08-12黄海生
李 哲 彭 鹏 黄海生
1(西安邮电大学电子工程学院 陕西 西安 710121)2(延安大学物理与电子信息学院 陕西 延安 716000)
0 引 言
随着无人机技术的发展,路径规划[1]成为研究热点,众多学者提出了一系列路径规划方法。基于图形的方法如Voronoi图法[2]和基于势场的方法如人工势场法[3-4],按照路径搜索方法可以分为决策型搜索方法如A*算法[5]、D*算法和随机型搜索方法如粒子群优化算法[6]、蚁群优化算法[7]、进化算法[8]、快速扩展随机树法[9],以及多种方法的组合应用[10-11]。基于流体计算的SIMPLEC法借鉴流体流动的性质进行路径规划,但只是将障碍物区域设为边界(即第二类边界条件),没有对可飞行区域风险程度进行区分。流体法的主要计算方法有数值法[12-13]和解析法[14-17],数值法适合全局路径规划,运算量较大,解析法能适合局部快速路径规划,但是综合环境因素能力较差。
为了解决人工势场、SIMPLEC法等传统势场法综合复杂环境因素能力弱的问题,提出建立磁导率线性过渡带的方法。在将障碍物设为边界区域的基础上,对可飞行区域根据飞行任务设置不同的相对磁导率(简称为磁导率)以更好地综合环境信息能力,建立障碍物、兴趣区域、飞行限定高度磁导率过渡带模型,将起点设为高磁势点,将目标点设为低磁势点,再利用有限元分析法生成全局磁场方向进行路径规划,最后对生成路径进行评估检测。
1 磁场特点和路径规划
人工磁场法利用现存磁场特性进行路径规划,用到的磁场为无源磁场[19]。以下是无源磁场和路径规划相关性质的论证,包括连通性、避障性、边界突变性。
1.1 连通性
磁场连通性是指磁感线总是从高磁势点指向低磁势点,且磁通密度B在磁导率不发生突变的情况下总是连续变化的,则穿过闭合曲面S的磁通量ψ为:
ψ=∮SB·dS
(1)
对式(1)应用散度定理:
(2)
式中:V为闭合曲面S所包围的体积,穿过一个封闭面S的磁通量等于离开这个封闭曲面的磁通量,即磁通线永远是连续的。路径规划的目的是从出发点到目标点规划出一条路径,磁感线的闭合性和连续性符合这个特点。
1.2 避障性
依据磁屏蔽效应,磁场边界和空穴处磁场分布符合齐次诺曼边界条件。在边界和空穴处,磁势下降方向垂直于交界面,n为法向单位向量,磁势下降方向和交界面法方向关系如下:

(3)
式中:Vm为磁势下降方向。
磁场方向垂直于磁势下降方向,满足路径规划中的避障要求。
1.3 边界突变性
为了拓宽流体场理论在三维路径规划中的应用,在非障碍物区域设置为不同磁导率的材料。不同磁导率区域交界处存在磁场方向突变的情况,磁导率突变边界的磁场方向性质如图1所示。

图1 磁导率突变边界条件
由恒定磁场的两个基本方程∮SB·dS=0和∮CH·dl=I,其中:dl为环路线元;I为环路电流。可得到磁场的边界条件:
(4)
式中:n为法向单位向量;t为切向单位向量;B1n和B2n分别为分界面两侧磁通密度的法向分量;H1t和H2t分别为分界面两侧磁场强度的切向分量。由式(4)知,在分界面处的磁通密度B的法向分量连续,无源磁场电流面密度JS=0,所以磁场强度H的切向分量连续,此时有:
(5)
由式(5)知,磁导率突变边界有磁场方向突变情况,不利于产生平滑路径,所以提出磁导率连续过渡带方法。
2 人工磁场路径规划算法
2.1 环境建模
首先要进行环境信息提取,在物理仿真软件COMSOL上建立等比例的飞行场景模型,飞行区域和磁场内容对应关系如图2所示,提出了根据环境中障碍物、兴趣区域、高度限定要求建立磁导率偏移模型,然后进行网格划分,计算每个网格单元的磁场方向,最后在MATLAB中迭代生成路径。算法流程如图2所示。

图2 人工磁场路径规划算法流程
现实环境中的障碍物或者兴趣区域可简化为长方体、球体或其组合,故采用图3所示模型阐述人工磁场算法流程。
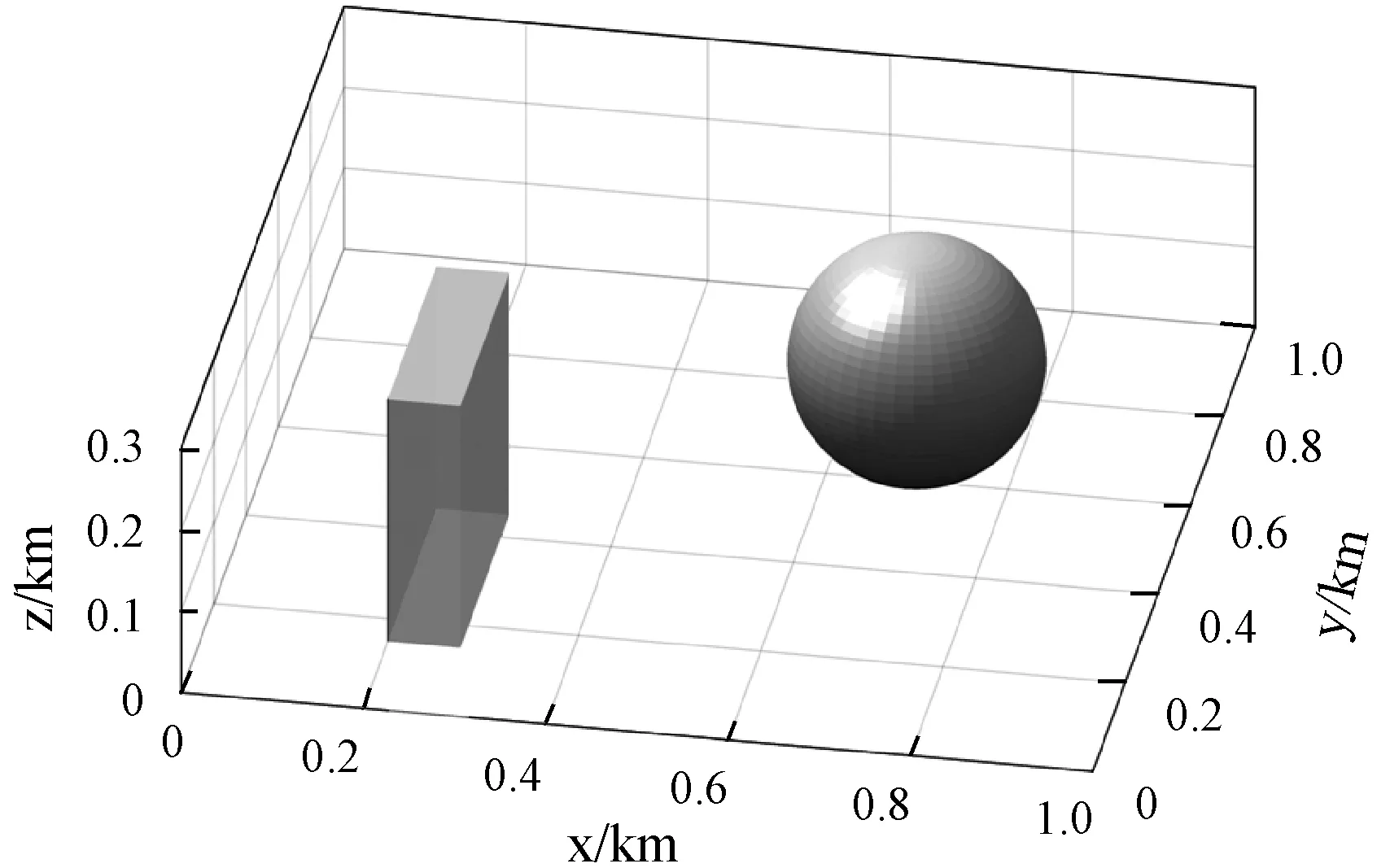
图3 示例模型
2.2 有限元分析求解
首先要对上述模型进行网格划分,采用Delaunay四面体网格划分法把飞行区域网格化[18-20],网格化后的飞行区域如图4所示。

图4 示例模型网格划分
采用整型数组n(i,e)将单元编码和节点编码联系起来。这里用i=1,2,3,4表示每一个四面体的四个顶点,而e=1,2,3,M,其中M表示四面体单元总数。在n(i,e)中,存储第e个单元中第i个节点的全局节点信息。每个四面体单元内磁势Ф近似为:
Фe(x,y,z)=ae+bex+cey+dez
(6)
将式(6)应用到单元的四个节点上可以确定四个系数ae、be、ce、de和单元体积Ve。将第j个节点上所得系数回代式(6)可得:
(7)
式(7)中插值函数为:
(8)
静磁场是以磁势Ф表示的无源场,可列泛函数如下:
(9)
式中:S1表示第一类边界面;S2表示第二类边界面;Ф0为已知磁势点。
将上述边值问题写为等价的泛函数极值问题:
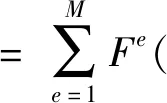
(10)
式中:M表示体单元总数。Fe由式(11)给出。
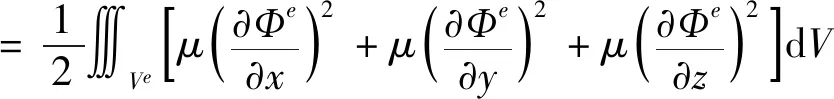
(11)

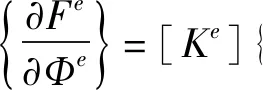
(12)
(13)
有了式(12)给出的单元方程后整合所有M个单元得到方程:
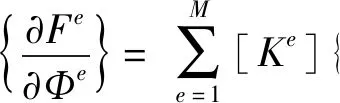
(14)

(15)
示例模型在z=0.15 km处磁场方向的大致分布如图5所示。
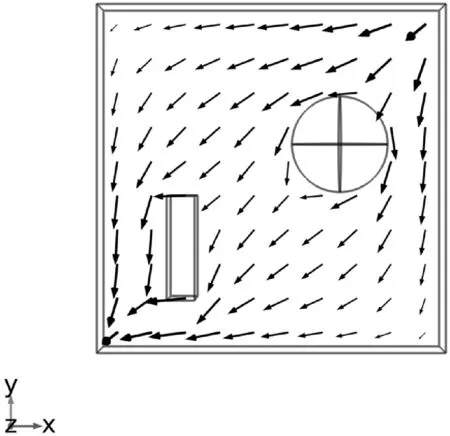
图5 磁场强度方向分布
2.3 飞行路径生成
(1) 初始迭代方向选择。磁场有限元分析法理论上会生成无数条磁通流线,出发方向的选择对路径的质量影响较大,要选择磁势下降最快的方向,在一个以起点为球心、10 m为半径的球面上检测磁势最低的点,以起点和球面上最低磁势点的连线作为初始迭代方向。
(2) 迭代生成路径。在确定好初始迭代方向后,从起点开始迭代,沿着飞行器当前所在单元的磁场方向He移动步长u,为了表示每一条路径L的形式,设任意一条路径中有n个节点(包括起始点和终点)。
L=(p1,p2,…,pi,…,pn) 1≤i≤n,n≥2
(16)
式中:p1为起点坐标;pn为终点坐标;pi为第i个节点的坐标。pi+1和pi的迭代关系如式(17)所示,从p1开始迭代直到最新点和终点距离小于设定值。

(17)
(3) 路径检测。对所得路径进行无人机运动学检测,若不符合则调整模型参数,重新生成路径直到生成路径满足要求为止。
2.4 路径评估函数的建立
用相邻两路径段pi-1pi和pipi+1夹角的余弦cosθi评估路径平滑度,函数值越大路径越平滑。路径平滑度评价函数f1[21]为:
(18)
式中:n表示路径节点数。
路径风险评估函数f2的建立。计算每一个路径点pi到各个障碍物最近点的距离d和障碍物表面风险参数V以评估路径的风险,计算如式(19)所示,函数值越小路径风险越小。
(19)
式中:m表示障碍物个数;n表示路径节点数。
3 磁导率偏移模型
为了将不同障碍物危险程度和飞行任务要求体现在磁场模型中,首先依据SIMPLEC流体场算法,将障碍物实体对应为磁场中的空穴;其次对可飞行区域处理,对可飞行空间中各个位置设统一的较高磁导率,称为基准磁导率μs;然后分别对障碍物、兴趣区域、飞行高度限定建立不同的磁导率偏移模型函数Δμ;最后将所有飞行区域组成部分的磁导率偏移模型函数Δμ叠加到基准磁导率μs上,生成磁场方向以进行路径规划。
3.1 障碍物磁导率偏移模型
在无人机飞行任务中,不同障碍物具有不同的危险程度,比如某些山体有泥石流滑坡威胁。为了将这种危险系数随距离障碍物变化的情况加入到路径规划影响因素中,提出磁导率过渡带障碍物模型,以过渡带厚度(R1-R0)和风险程度V正比关系作为建模依据,障碍物风险越大,过渡带厚度越大。建模时,障碍物内部依旧对应为磁场内部空穴,在障碍物外部建立磁导率偏移过渡带函数,以球型为例建立障碍物磁导率偏移模型函数Δμa:
(20)
式中:μ0表示空穴;r为自变量,代表当前点距离球心的距离;μ1表示障碍物实体边缘偏移磁导率;R0表示球形障碍物半径;R1表示球形障碍物过渡带半径;Ω0为障碍物实体内部;Ω1为障碍物外部过渡带。过渡带模型示意图如图所示6所示,图中S和E点分别为出发点和目标点。
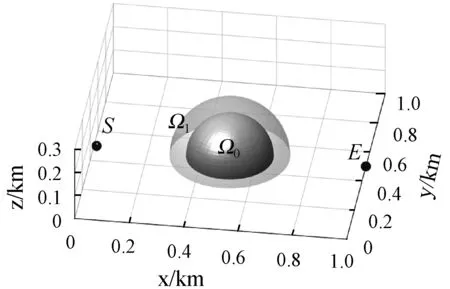
图6 障碍物磁导率偏移模型
3.2 兴趣区域磁导率偏移模型
在无人机飞行任务中,往往有些区域是飞行中的感兴趣区域,路径规划需要经过这些区域。以球形兴趣区域为例,磁导率偏移函数如下:
(21)
式中:μ3表示较高磁导率;R0表示兴趣区域半径;R1表示兴趣区域磁导率过渡带半径;Ω2为兴趣区域内部;Ω3为兴趣区域外部过渡带。兴趣区域模型磁场方向分布如图7所示,可以看出,磁导率渐变过渡带使磁场分布连续,不会出现突变情况,且对磁场分布的扰动能力增强。

图7 兴趣区域模型流线
3.3 飞行高度限定磁导率偏移模型
根据飞行高度要求,将在限定高度之下建立磁导率线性过渡带,将目标高度之上设为低磁导率,以此建立了飞行高度限定磁导率偏移函数如下:
(22)
式中:z表示空间中某点的高度;h表示限定高度;μ4表示z>h位置的偏移磁导率;k表示磁导率从地面向高处的变化率。
3.4 模型重叠区域μ的处理
不同模型存在重叠情况,为了保证全局磁导率连续,就要保证磁导率分布的连续,在模型重叠区域做磁导率数值叠加处理,其中障碍物实体内部不叠加保持空穴,叠加公式如下:
(23)
式中:l、m分别表示为障碍物、兴趣区域数量。
4 综合仿真和分析
4.1 飞行高度约束与避险综合仿真
为了人工磁场测试障碍物模型和飞行高度限定模型的综合路径规划性能,进行了若干组不同限定高度的避障对比实验,仿真环境设置I、II和II三个障碍物,风险系数V=0.1,其中:仿真一的限定高度为0.1 km;仿真二的限定高度为0.2 km;起点为(0,0.5,0) km;终点为(2,0.5,0) km;k=2 000。飞行环境信息见表1。

表1 障碍物和飞行限高综合仿真飞行环境参数
仿真结果如图8和表2所示,生成路径在保证平滑度和距离障碍物保持安全距离的条件下分别实现了限高0.1 km和0.2 km的避障飞行任务,满足飞行高度路径长度占比分别为79%和73%。
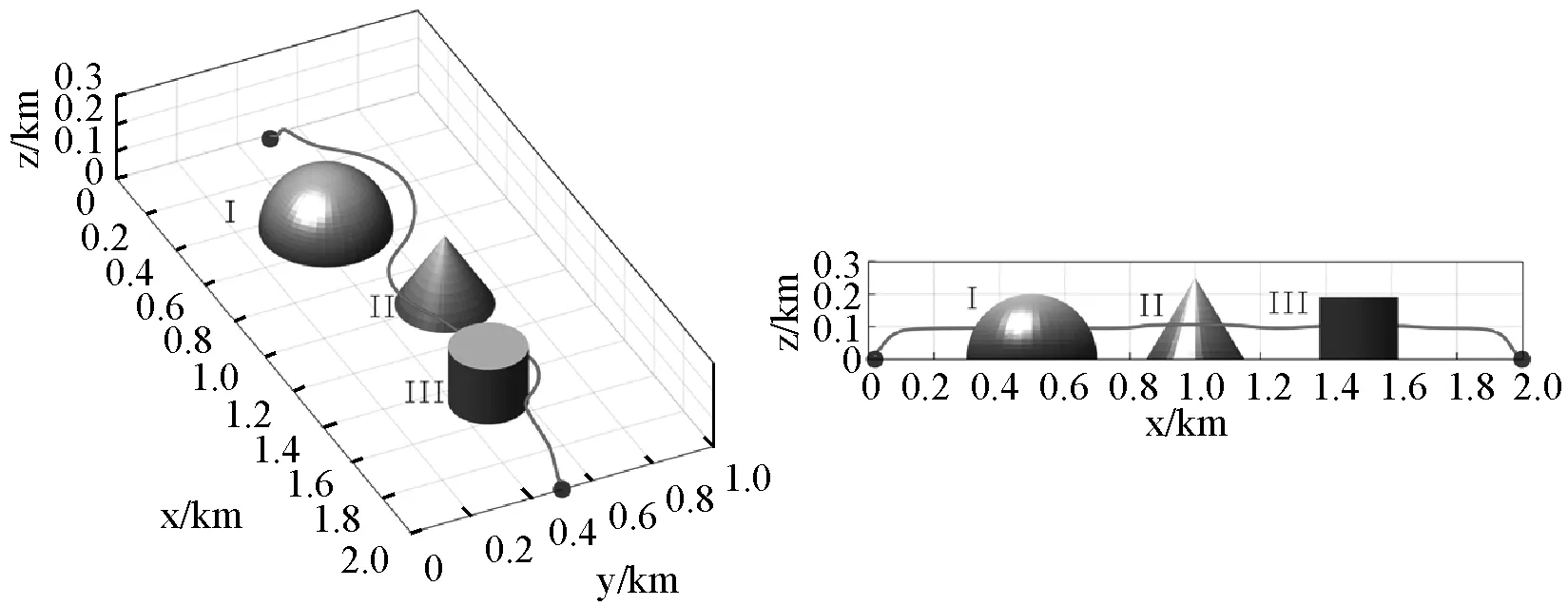
(a) 限高h=0.1 km 3D视图 (b) 限高h=0.1 km 2D主视图

表2 不同飞行高度限定仿真结果对比
4.2 算法对比
为测试障碍物模型和兴趣区域中的综合路径规划性能,分别使用SIMPLEC法、人工势场法和人工磁场算法进行路径规划。对于兴趣区域,在实验环境设置I和II两个圆柱形障碍物,预设障碍物I风险系数V1=0.12大于障碍物II风险系数V2=0.04,故设障碍物I的过渡带大于障碍物II,过渡带内外边缘偏移磁导率分别为Δμi和Δμo,III为圆柱形兴趣区域,设起点为(0,0.5,0.15) km,终点为(2,0.5,0.15) km,飞行环境信息见表3。
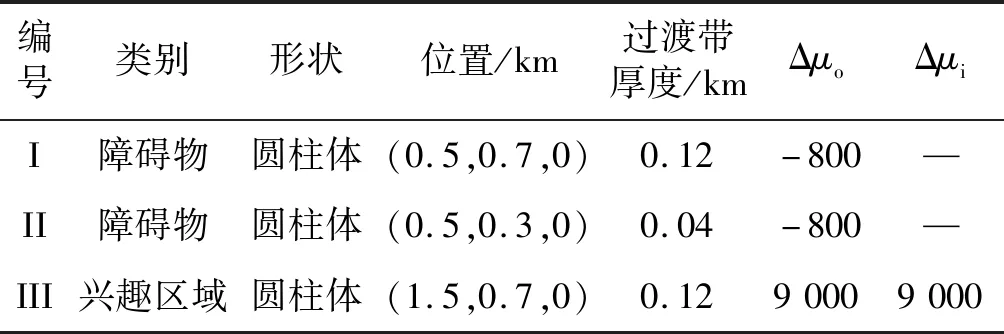
表3 障碍物和兴趣区域综合仿真飞行环境组成
三组仿真结果见图9和表4。可以看出三种方法均能规划出从起点到终点且完成避障和兴趣区域巡视的路径规划,人工磁场法的路径平滑性能、兴趣区域搜索性能、避险性能比传统SIMPLEC分别提高了4.6%、3.1%、21.01%,比人工势场法分别提高了4.3%、47%、12.14%。
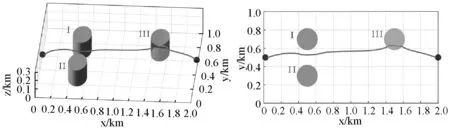
(a) SIMPLEC法3-D视图 (b) SIMPLEC法平面俯视图

表4 不同算法仿真结果对比
5 结 语
本文提出一种人工磁场的三维路径规划方法,该方法以人工磁场方向生成路径,在建模过程中,在可飞区域根据风险程度设立磁导率偏移模型。仿真证明了人工磁场算法能完成扩大障碍物扰动磁场、兴趣区域搜索、定高飞行等复杂飞行任务,同时满足路径平滑和无人机动力学约束。仿真数据表明:
(1) 人工磁场法可实现传统势场法不具备的飞行高度限定路径规划,路径规划均可保持70%以上路径长度满足设定飞行高度。
(2) 人工磁场法在路径平滑性能、兴趣区域搜索性能、避险性能上比传统SIMPLEC法和人工势场法更具优势,在路径长度方面与传统SIMPLEC和人工势场法相当。其扩展了势场法在避险路径规划与决策上的应用,具有应用价值。
