基于Spark字典表压缩存储的关联规则算法优化

刘丽娜 姜利群

(广州工商学院计算机科学与工程系 广东 广州 510850)

0 引 言

数据挖掘的概念已提出多年，其宗旨在于从海量数据中分析出对现阶段或未来有意义的数据信息，它涉及的经典算法分类有频繁项集生成[1]、频繁模式增长[2]和垂直格式等[3-4]。其中频繁项集生成的关联规则(Apriori)算法尤为经典，用于挖掘数据元素之间的关系，如通过关联规则可以得出是吃米饭的家庭离婚率高还是吃面食的家庭离婚率高[5]。关联规则是在海量元素中找出元素之间的有趣关系。频繁模式增长的代表算法是FP-growth[6]，其基本原理是将频繁项集规约至一棵模式树中并根据条件按需挖掘。垂直格式主要针对数据维数及属性较低的数据模型，以数据维数即列项作为行标，将事务项作为列标，从而达到压缩数据库的目的[7]。

面对数据大爆炸的信息时代，传统的数据处理速率已无法应对庞大的数据量，同时无法满足人们的需求，而Spark技术的出现弥补了该缺陷。Spark是在Hadoop的基础上进一步改进以适用于大数据分析，当数据集全部载入内存且条件满足的情况下其速度可比Hadoop快100倍之多[8]。但软件的更新有限，数据的增长无限，刘莉萍等[4]指出，在Spark的并行处理之路上内存及数据是未来两大研究突破点。

基于上述问题，本文在Spark的列式存储技术的基础上进行不断压缩剪枝，接近断层式地减少数据量加快并行处理速度，通过实验验证该算法适用于分析各种结构化数据集。

1 相关研究

Apriori最初由Agrawal等[9]提出，后续学者为不断提高运行速度对其进行了无数次改进。Han等[10]提出较具代表性的基于FP-tree的FP-growth算法，该算法从减少数据库遍历次数降低I/O消耗的角度考虑，由各个元素组成节点，只需遍历一次数据库，无候选频繁项集产生，但由于需在内存中创建FP-tree拓扑结构消耗大量内存且只适用于分析单维类型的大数据。文献[11]最初提出的Eclat算法是从减少数据量的角度分析，该算法通过颠覆数据存放常态减少重复元素，以每行中事务项的列元素转为行标，而该列元素所出现的事务项转为列标从而减少元素的重复次数以便于支持度计数，但该算法的运行效率与数据的特征息息相关，其元素个数越少事务项越多效率越高，在维数越多属性值越多的多维数据中效率趋近于原始Apriori算法的效率。Yang等[12]提出通过抽取海量数据中的部分样本减少数据执行量的抽样加权向量矩阵法来对Apriori算法进行优化，该改进算法虽通过抽样减少了数据量，但可能丢失一些特殊点规则。

近几年并行处理兴起，Hadoop的MapReduce框架仅通过Map函数和Reduce函数即可分布执行Apriori，数据量越大节点加入越多执行效率越高，Hadoop的MapReduce框架处理的简单性既是优点又是缺点，只需执行Map算子和Reduce算子却不能满足现如今数据处理的复杂性以及人机交互的高要求。因此，Spark应运而生，内存模型、快速的迭代处理优势、更支持交互查询等诸多优点使其迅速崛起。黄剑等[13]在2017年提出基于Hadoop平台的改进算法，该改进算法减少了候选集的产生，以布尔矩阵的模式压缩数据集进行并行处理，从而多方面加快数据的处理速度，但该算法并未表明可以处理多维多属性的数据，且有一定量的候选频繁项集产生，存在一定的约束性。闫梦洁等[14]在2017年提出了基于Spark的Apriori优化算法IABS，实验表明在同等条件下Spark执行Apriori比Hadoop的效率更高，且其采用YAFIM将候选频繁项集存进哈希树加速候选频繁项集的查询，让算法的效率得到进一步的提高。但IABS算法在第一阶段产生的候选频繁项集及查询自连接操作的复杂性一定程度上约束了算法的效率，同时该算法在处理数据的维度属性的一般性及特殊性上并未做相应说明。由于篇幅有限，本文不再赘述，详细研究见参考文献[15-19]。

随着数据量剧增、I/O消耗及有限内存的约束，算法的运行代价与日俱增，减少其数据量与降低内存耗费是未来丞待解决的两大难题。本文依托Spark计算框架，从处理多维多属性数据集的角度，消除候选频繁项集，最大限度减低算法自连接时间提升Apriori算法的执行效率，提出IApriori算法(improved Apriori algorithm)。

2 构建关联规则算法优化模型

2.1 算法介绍

Apriori算法分为剪枝和连枝两个步骤。首先从候选集Ci中统计支持度，根据最小支持度SupMin剪去不合规格的元素e或连枝后的事务集t得到频繁项集Li，再从频繁项集Li∞Li连枝得到新的候选集Ci+1，如此循环迭代直到候选集为∅，由此得到所有的规则。

设数据库D={t1，t2，…，tm|m>0且m∈N}，每项事务t={e1，e2，…，en|n>0且n∈N}，e为事务项里包含的元素。

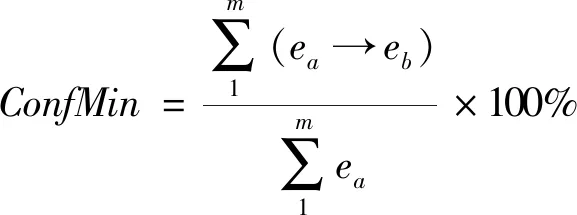
2.2 构建Spark计算框架

Hadoop虽提供同样的分布式处理模式，但其只支持Map和Reduce两个算子，限制了复杂场景的数据分析能力。Spark计算框架作为Hadoop计算框架的继任[8]，提供了更为丰富的API，且其能将中间结果写入内存的特性减少了数据的I/O，加速数据的分布处理。本文中Spark计算框架的搭建相对复杂，第一阶段以R在RStudio平台上分别在master节点和slave节点中安装JDK，配置Hadoop及其环境变量，然后配置YARN、HDFS、HBase、Hive等，及其他组件和依赖包，配置完成后启动Hadoop集群；第二阶段配置Spark、配置环境变量及相关依赖包；第三阶段采用Java运行改进的关联规则代码，Spark读取HBase形成RDD，存入Hive。

本文所依托的Spark计算框架采用了主从节点结构的计算模型，如图1所示。主节点master对从节点slave进行任务调度分布，slave节点在执行完job后将结果再返回master进行汇总，模型同时采用R结合Java对环境进行配置和算法执行。

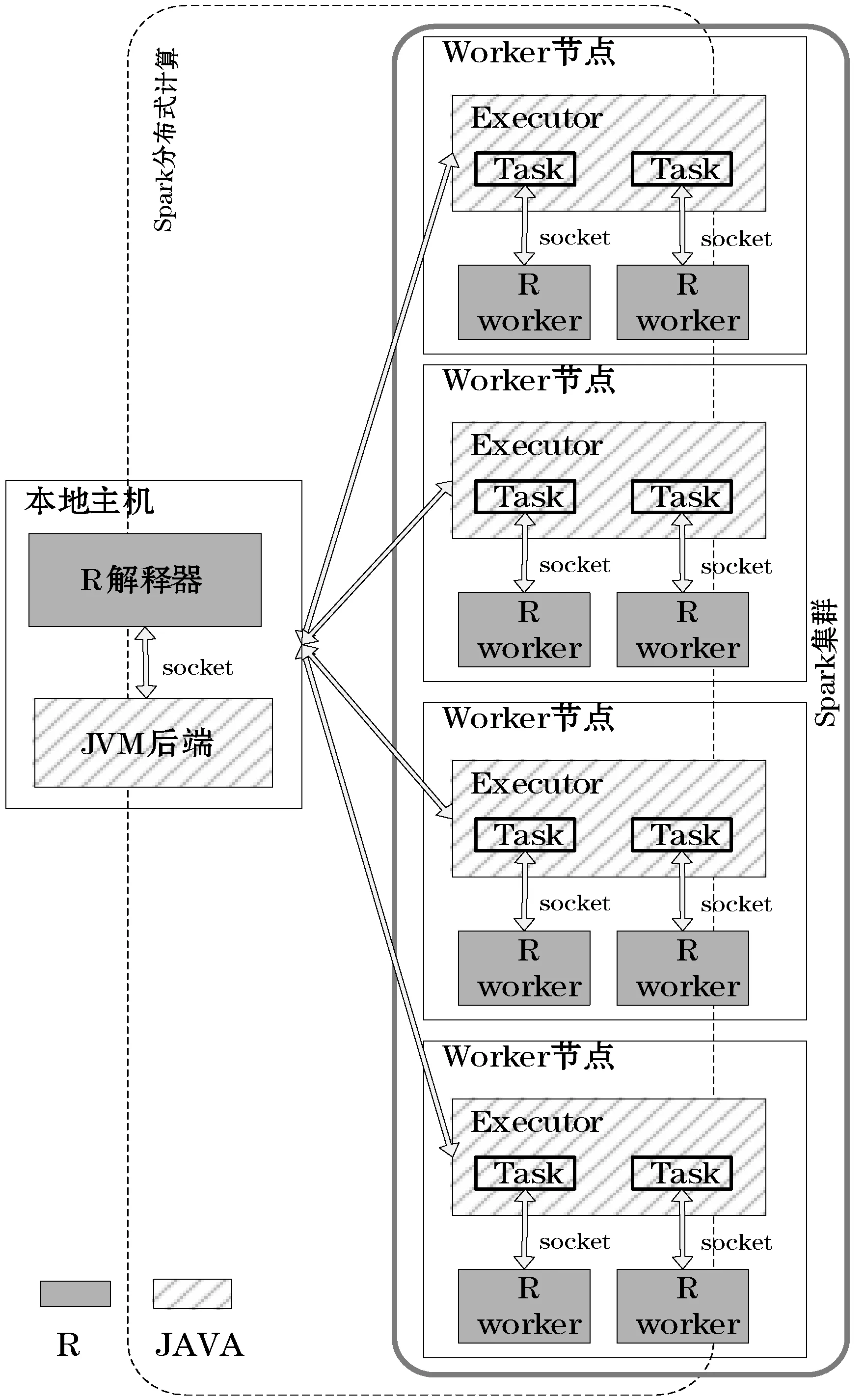
图1 Spark计算模型

2.3 字典表压缩存储多维多属性并行方案

以往的Apriori优化基本以清洗转化后的单维度布尔值为研究数据，而一般情况下，海量数据分为结构化数据与非结构化数据，且结构化数据不仅多维更兼多属性。在数据预处理转换为布尔矩阵时不仅前期需耗费大量的时间，且清洗之后的每个属性值会根据占比消耗大部分的空间用于存储“0”值。

假设有100条事务，每条事务有5个维度，每个维度有3个属性值，原本的存储空间为500(100×5)，而转换为布尔矩阵之后的空间为1 500(100×(5×3))，则存储空间的耗费量为原先的3倍，属性值的个数x与空间耗费率为原本存储空间η的x倍，即xη。

2.3.1基于HBase的行转列式存储

1) 常规行存储模式。常规行存储模式如图2所示。行存储的遍历思想如下：从事务项的第一行自左到右遍历至第一行结束，再从第二行以之前的模式遍历，以此类推直至遍历完所有数据。按照上述遍历思想可得到如下一般形式：

图2 行存储模式

e11,e12,…，e1i;e21,e22,…，e2j;…;em1,em2,…，emk

(1)

式中：m表示有m行；i、j、k表示列，i、j、k的取值可等或不等。

结合图2，其步骤可以描述如下：

第一步访问第一行，可获取信息(e11,e12,…，e1i)。

第二步访问第二行，可获取信息(e21,e22,…，e2j)。

以此类推，第m步访问第m行，可获取信息(em1,em2,…，emk)。

2) 行转列式存储模式。Spark是在Hadoop计算框架的基础上进行了扩展，行转列式存储模式如图3所示。基于HBase的行转列式存储的遍历思想如下：从事务项的第一列自上而下遍历至第一列结束，再从第二列以之前的模式遍历，以此类推直至遍历完所有数据。按照上述遍历思想可得到如下一般形式：

图3 HBase列存储模式

e11,e21,…，em1;e12,e22,…,em2;…;e1i,e2j,…,emk

(2)

式中：m表示有m行，n表示最长的列数；i、j、k表示列，i、j、k的取值可等或不等。

第一步访问第一列，可获取信息(e11,e21,…，em1)。

第二步访问第二列，可获取信息(e12,e22,…，em2)。

以此类推，第m步访问第n列，可获取信息(e1i,e2j,…，emk)。

2.3.2字典表数据压缩

首先，统计每一行的支持度σ，当支持度σ≤SupMin时，进行第一轮的剪枝，得到频繁一项集。为便于理解，数据表中的元素e代入具体实例进行演示(限于篇幅，假设实例数据已进行过第一轮剪枝)。将表中对应的属性值按ID及列的方式存储为字典表，将属性值转换为占内存较少的整型数值(或字符)，如图4所示。

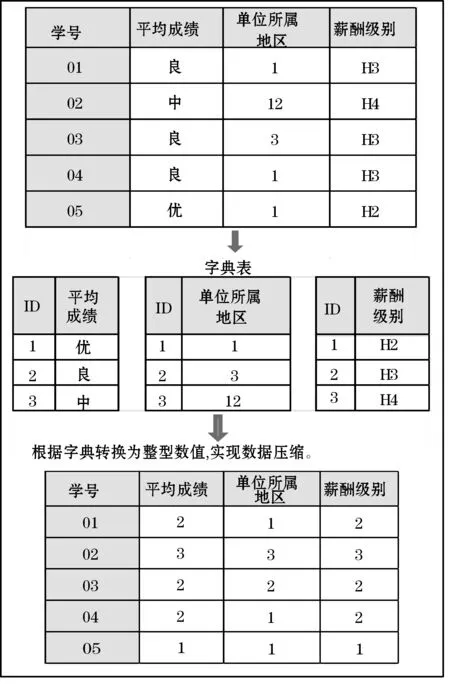
图4 字典表数据压缩

在该步骤中，根据元素的n个维度构建n个字典表，字典表由ID号及维度属性值构成，不同的属性值对应该表中唯一的ID号。如该实例中薪酬级别维度字典表中“H2”属性值对应的字典表ID号为“1”，平均成绩维度字典表中“良”属性值对应的字典表ID为“2”。在构建完字典表之后，根据维度字典表属性值对应的ID号将数据集替换压缩为整型数值表。该方法能在有效压缩数据集的同时，便于为下一步的“与”操作铺垫。

2.3.3基于字典表压缩的连枝剪枝设计

将2.3.2节的频繁一项集进行字典表对应压缩后，执行行转列式存储，将原存储的行事务项t转为列，而元素维度转为行，如图5所示。同时统计每个维度字典表中各个属性值的计数，为计算置信度ξ做数据准备。列式存储在操作时只有涉及到计算的列会被读取，减少I/O消耗加速算法执行数据分析。

（1）色彩管理系统（CMS）与数码打样色彩管理是CTP 系统中较为关键的技术，也是用于地图印刷质量控制的核心。它将创建了颜色的色彩空间与要输出该色的色彩空间进行比较，使要处理的地图文件在流程中的各个输出端（如屏幕显示、打样、印刷）上显示的颜色尽可能保持一致。因此就要在数据输入、处理、输出时进行RGB 模式到CMYK 模式的转换，由可校色的高质量显示器近似模拟印刷效果，打样输出采用国际通用的ICC 标准，配备专业数码打样软件输出数码样张，经过色彩管理后的数码打样，能够完全模拟印刷机的色彩曲线，输出与印刷品感官色彩完全一样的数码样张，提供客户做印前检查，印前可即时进行修改，且色彩稳定。

图5 基于字典表压缩的连枝设计

该步骤从第一列开始，逐列进行读取，对每列的每个字典表ID值从“1”到“n”进行查询，并逐一转换为布尔值。如第一次查询到第一列存在字典表ID 数值为“1”，则将其替换为布尔值“1”，其他值替换为布尔值“0”，第二列执行同样操作，之后第一列与第二列执行“与”操作，将结果计算得出频繁项集、支持度σ及置信度ξ，再替换回原来的值，列与列依次读取并执行“与”操作直至存在值为“1”的最后一列；第二次查询第一列字典表ID数值为“2”，则将“2”替换为布尔值“1”，其他值替换为布尔值“0”，第二列执行同样操作，之后第一列与第二列执行“与”操作，将结果计算得出频繁项集、支持度σ及置信度ξ，再替换回原来的值，涉及操作的列与列依次读取并执行 “与”操作直至存在值为“2”的最后一列；依次操作，直到替换完字典表最大ID值n，完成所有维度属性值的“与”操作。该步骤的遍历操作顺序如图5所示，详细的实例替换操作如图6所示。

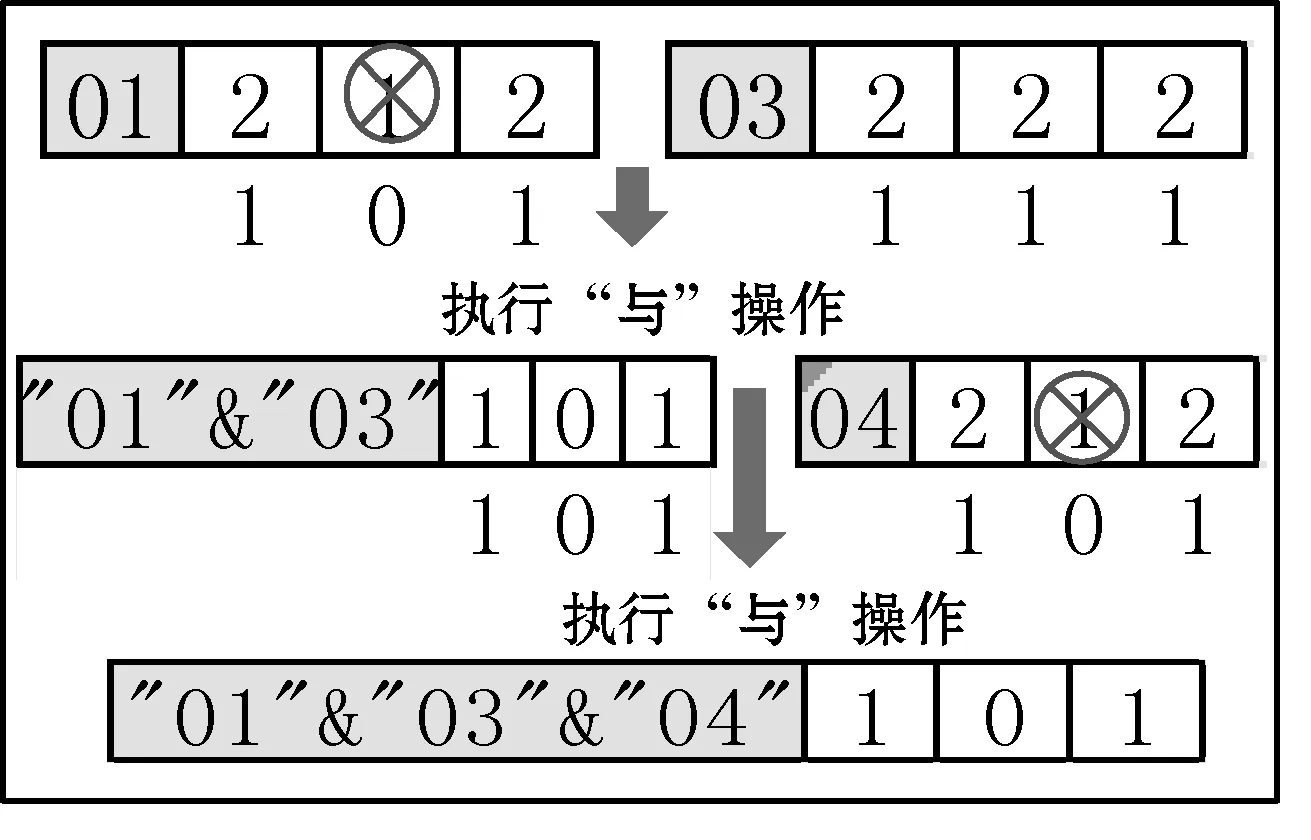
图6 字典表压缩的剪枝设计

本文取实例中第二次查询替换维度属性值“2”为例，如图6所示，将学号“01”列中找到所有字典表ID数值为“2”的单元，并将其转换为布尔值“1”，其他维度属性值替换为布尔值“0”。根据该思想，本例中学号“01”列的原值为(2,1,2)，替换之后值为(1,0,1)，而实例中学号“02”列原值为(3,3,3)(见图5中的实例列表)，对比该列无可替换值，无“与”操作价值，因而可跳过该列执行下一列，学号“03”列的原值为(2,2,2)，替换之后值为(1,1,1)，可与“01”列执行“与”操作，即(1,0,1)&(1,1,1)=(1,0,1)，计数器加1；计算支持度σ=1/5=0.2(第一次“与”操作计数，此时计数器为1，总列数为5)；假设最小支持度、置信度为SupMin=ConfMin=0.2，符合最小支持度， 则频繁项集Lφ频繁项数φ等于“与”操作结果中所有布尔值为“1”的和，即φ=1+0+1=2；“与”结果布尔值为“1”对应元素下标为关联规则元素，即频繁二项集的L2={[e1]2，[e3]2}，其中：规则([e1]2→[e3]2)置信度ξ=1/3=0.33(第一次“与”操作计数，此时计数器为1，在每个维度字典表中各个属性值的计数中e1列中属性值字典表ID值为“2”的计数值为3)，置信度ξ=0.33>ConfMin，符合要求；频繁二项集L2={[e1]2，[e3]2}对应第一行及第三行的维度名，{[平均成绩]2，[薪酬级别]2 },方括号后的“2”为替换维度属性值“2”，对应字典表ID值为“2”的属性值从而得到频繁项集L2={平均成绩.良，薪酬级别.H2}；将“与”操作完的列“01”及“02”还原为原来值。

取学号“04”列的原值为(2,1,2)，替换之后值为(1,0,1)，和“01&03”的“与”结果值(1,0,1)做再次“与”操作，即(1,0,1)&(1,0,1)=(1,0,1)，计数器加1；计算支持度σ=2/5=0.4(第二次“与”操作计数，此时计数器为2，总列数为5)，支持度σ=0.4>SupMin，符合要求，则频繁项集Lφ频繁项数φ等于“与”操作结果中所有布尔值为“1”的和，即φ=1+0+1=2；“与”结果布尔值为“1”对应元素下标为关联规则元素，即频繁二项集的L2={[e1]2，[e3]2}，其中：规则([e1]2→[e3]2)置信度ξ=2/3=0.66(第二次“与”操作计数，此时计数器为2，e1列中属性值字典表ID值为“2”的计数值为3)，置信度ξ=0.66>ConfMin，符合要求；频繁二项集L2={[e1]2，[e3]2}对应第一行及第三行的属性名，{[平均成绩]2，[薪酬级别]2 },其中方括号后的“2”为替换维度属性值“2”，对应字典表ID值为“2”的属性值从而得到频繁二项集L2={平均成绩.良，薪酬级别.H2}；将“与”操作完的“04”列还原为原来值。

基于以上思想，假设σ≥SupMin且ξ≥ConfMin，则存储计算结果的“行”下标，且“行”下标所记的元素及e及循环次数i可以得到频繁φ项集Lφ，而无须产生候选集。因此，Lφ={[ek]i,[ek+1]i,…,[en]i}，其中i为外层循环计数器，即替换值，根据元素下标及字典表得到相应的频繁项集。

定义3en为存放“与”操作结果的数组，频繁φ项集Lφ，其中φ的值等于“与”操作后“1”的和，从而得到一般形式下频繁项集Lφ的项集数φ的计算式为：

(3)

定义4Counter为“与”次数计时器，从而得到一般形式下频繁φ项集Lφ的支持度σ和规则(ei→ej)的置信度ξ计算公式分别如下：

(4)

(5)

式中：Counter(ei→ej)为规则(ei→ej)的“与”计数；Count(ei)为元素属性值ei在数据库中的统计数。

2.3.4改进算法IApriori实现

Spark的优势是能在内存保存job的中间结果，降低I/O提高执行效率。该算法利用HBase列式存储的特点，通过调用f算子转存、g算子运算及h算子迭代生成RDD，算法实现步骤见算法1。

算法1IApriori算法

输入：数据库D。

输入：最小支持度SupMin，最小置信度ConfMin。

1. for 1 tom

//m为事务项数

//计算每个维度属性值ej的统计数

3. if(σj≤SupMin) deleteσi;//在列维度中，先进行每

//一列的支持度σ统计，如σ≤SupMin则先进行第一轮的剪枝

4. end for

5.f(ti，ej)=g(ej，ti);//构造函数，对事务项ti、事务项维

//度数ei进行行转列式预处理

6. 抽取字典表T;

7. for 1 ton

//遍历元素值“1”至“n”

8. fore1toen

//遍历事务项的属性值

9. if(ej=j)ej=1;

//转换为布尔值

10. elseej=0;

11.φ=h(ei&e(i-1));

//构造函数，“与”操作后计算“1”的和

12. if(ti=1)a[k]=ti;

//构造数列a存储“位”为1的行标

13. if(((i/n)>SupMin)&&((i/σj)>ConfMin))

14.σ=i/n;ξ=i/σj;Lφ={a[k]};

//σ为支持度，ξ为置信度

15.Lφ={a[k]};

//与字典表匹配

16.输出Lφ频繁项集;

17.输出σ和ξ;

//输出支持度及置信度

18. end for

19. end for

3 算法性能评估

3.1 分布式计算环境配置和部署

本实验在青软大数据平台下的虚拟机中完成，本实验采用1个master、4个slave共5个节点组建集群。每个节点采用CentOS 7版本64位操作系统，内存(RAM)3.88 GB可用，主频2.60 GHz，软件环境采用Hadoop2.6+Spark2.1+JDK1.8+SparkR、R、Java。首先以R语言部署安装JDK，Hadoop及其环境变量并依次配置YARN、HDFS、HBase、Hive等及组件和相关依赖包，配置完成后启动Hadoop集群。然后在Hadoop集群中以不同数据量和不同节点执行Apriori算法。最后再以R语言部署安装Spark、配置环境变量及相关依赖包，在该环境中执行Apriori算法和列阵压缩改进的IApriori算法。

实验数据集取近十年若干个高校的学生信息约15万条，为验证算法的性能拷贝模拟数据至200万条，数据量大小为146 MB，数据共有79列。

3.2 实验结果分析

本实验通过弹性分析算法在不同数据量及节点数的执行指标来评价改进算法IApriori的性能。通过对数据进行随机取样，在数据集不同，最小支持度SupMin=0.05的情况下的时间运行对比如图7所示。IApriori算法在相同的数据集不同节点数上的运行时间对比如图8所示。

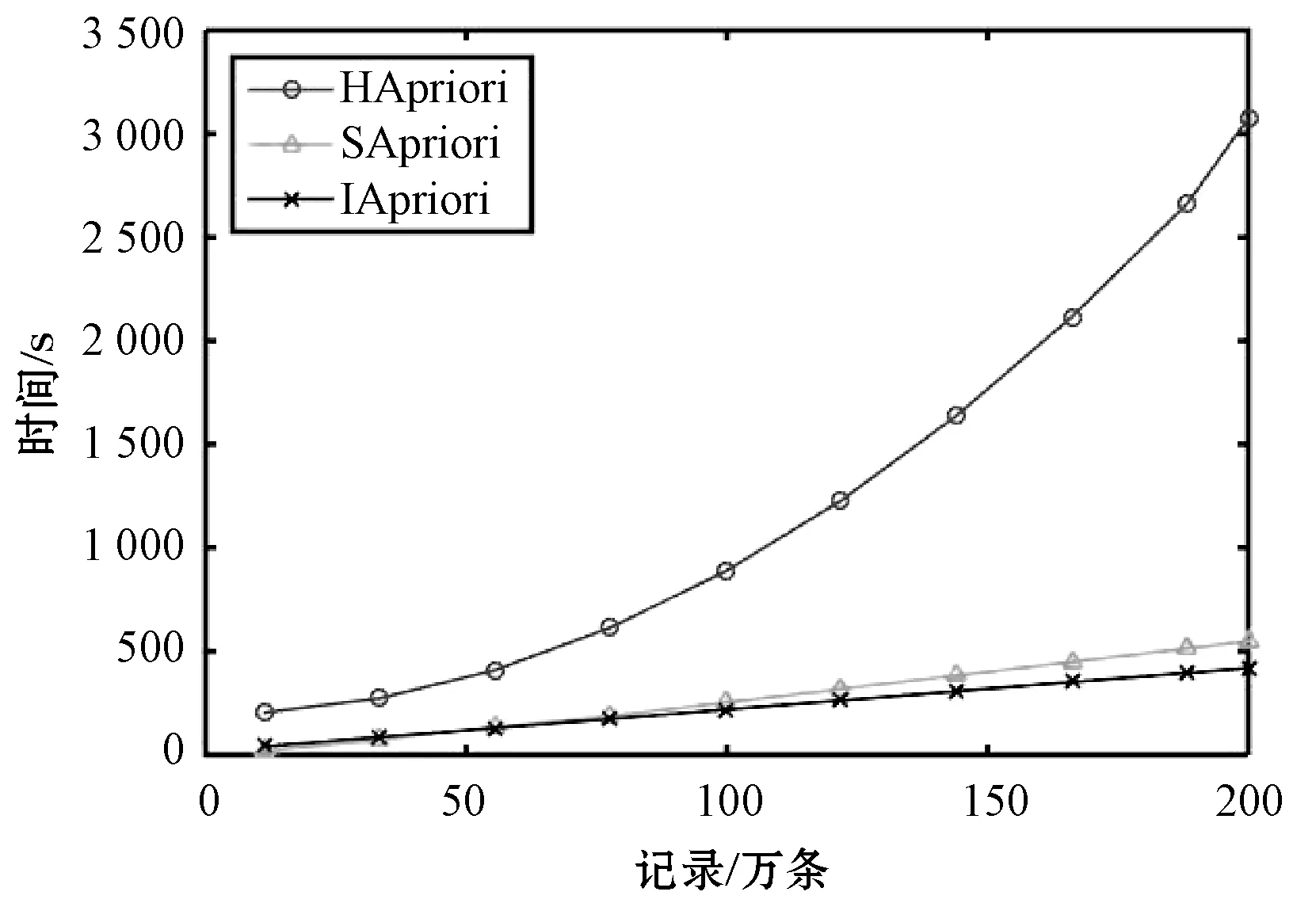
图7 不同算法运行时间对比

图8 不同算法在不同节点个数时的执行时间

由图7可见，在Hadoop计算框架中执行Apriori算法的效率要明显低于基于内存运算的Spark框架。同时可以看出改进算法IApriori在数据量较少时执行效率较低，因为改进的算法采用的存储方式需执行附加的步骤。但随着数据量不断加大，其执行效率高于同在Spark执行的Apriori传统算法(SApriori)，而随着节点数不断增加，改进算法IApriori的执行效率显著提高。

在不同节点数的弹性的对比分析中(如图8所示)，在节点数分别为2、3、4和5时，Hadoop框架由于数据I/O消耗时间及Apriori算法本身产生过多的候选频繁项集而拉低了算法的执行效率，在同一节点数执行相同数据集总比Spark计算框架耗时；而改进后的IApriori算法的效率优于原来的Apriori算法，但由于附加了行转列式存储时间及对数据字典表的加工时间而拉低了整体的效率，而未加改进的Apriori算法在执行数据前需增加大量的情况，则认为其清洗转换工作并未包含在算法执行时间内。因而，改进算法IApriori与原算法Apriori在数据集的执行效率表现中优势差距不非常明显。

4 结 语

针对Apriori算法存在产生大量候选频繁项集和多次遍历数据库增加I/O消耗的缺陷，本文在基于Spark多节点分布式执行算法的基础之上提出了一种改进的算法。本文算法在Spark计算框架上采用HBase列式存储，构建数据字典表，在计算过程中压缩原本庞大的数据量，同时简化连枝剪枝只需进行“与”操作，结合Spark分布式计算的特点使改进算法的执行效率在数据量不断增大的模型下得到有效提高。通过实验对比Hadoop计算框架下执行Apriori算法、Spark计算框架下执行Apriori算法及本文改进的算法，结果表明本文算法能分析多维多属性值的数据集，一定程度上节省了数据处理前清洗及转化工作，“与”操作后消除候选频繁项集的产生约省了内存计算时间及空间，在Spark基于内存的分布式处理框架下改进算法IApriori的执行效率得到有效提高。