基于FCM-XGBoost的大坝变形预测模型
2021-08-11杨晨蕾包腾飞
杨晨蕾,包腾飞
(1.河海大学 水利水电学院,南京 210098;2.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098; 3.三峡大学 水利与环境学院,湖北 宜昌 443002)
1 研究背景
大坝是一个复杂的非线性动力系统,变形值是反映坝体结构是否安全最直观的指标,对变形监测资料进行分析并作出合理预报,是水库安全运行的重要保障。随着技术的发展,大坝变形监测系统日趋完善,监测频率逐步提高,积累了大量的监测数据,若对全部测点逐个建模分析,将不利于及时反馈信息,难以得到大坝的真实运行状况[1];若建立单一模型分析所有测点,则预测精度往往无法满足要求。因此,如何平衡大坝变形预测效率和精度之间的关系,已成为一项重要的研究课题。
为了提高预测效率,并尽可能降低对精度的损失,本文首先引入聚类算法对变形测点分区,然后针对各个分区建模预测,这种方法因介于单一建模和逐个建模之间,能较大限度兼顾两者的关系。聚类是一种无监督学习算法,指按照特定标准把数据集划分为不同的类或簇。典型的聚类算法如K-means算法[2]计算速度快、操作简单,但聚类结果易受离群点的影响;基于层次的BIRCH算法[3]适用于大数据集的处理、时间和空间利用率高,但对非球形簇分类效果不佳;基于密度的DBSCAN算法[4]可以处理任意形状的类,但计算时间长、复杂度高。考虑到大坝的整体性,各变形测点之间往往存在某种内在关联,即离群点出现的概率很小,同时顾及到有些测点之间可能没有明显的类别界限,适合模糊聚类方法分析,因此本文引入融合了模糊数学理论和K-means算法的模糊C-均值聚类算法(FCM)来实现大坝变形测点的分区。
传统的大坝变形监测模型有统计模型、确定性模型和混合模型,这3种模型在非线性特征的处理上表现不佳,无法真实模拟大坝变形量与环境量之间的关系。为了弥补传统模型的不足,机器学习算法如BP神经网络、支持向量机(SVM)逐渐被引入到大坝安全监控领域[5],之后很长时间学者们致力于对这2种模型优化,取得了一定成果。例如,齐银峰等[6]针对传统BP神经网络收敛速度慢的缺陷,通过改进的粒子群算法进行优化,提出了一种改进的IPSO-BP模型;李涧鸣等[7]在传统SVM模型的基础上引入不敏感函数,并选用改进的混合蛙跳算法对参数寻优,达到了改善参数敏感性的目的。随后发展起来的随机森林算法,由于其具备更强的泛化能力和抗噪声能力,也被引入到大坝变形预测中,如罗浩等[8]建立了拱坝变形测点的随机森林预测模型,验证了它在预测精度上优于BP神经网络和SVM模型。然而,由于随机森林模型的训练集不能有缺失值,常常需要先进行缺失值填充处理,这也使得它的建模效率受到影响。
极端梯度提升XGBoost(eXtreme Gradient Boosting)算法是一种基于Boosting的集成学习算法[9],尤其适用于处理大坝变形这种原始数据多的大规模数据集,而且它的计算复杂度低,运行速度快、准确度高,可以同时满足对大坝变形预测时效性和准确性的要求。它还建立了对缺失值的自动处理机制,可以更好地解决大坝变形监测资料数据缺失的问题。该算法目前已在电力短期负荷预测[10]、铁路旅客退票率预测[11]等多个领域得到应用,并取得了不错的效果。综上,本文提出一种基于FCM-XGBoost的大坝变形预测模型,在提高预测精度的同时,也大大提高了预测效率。
2 算法介绍
2.1 FCM聚类算法
大坝的变形测点在水位、温度、时效等因素的作用下,在变化规律上具有一定的相似性,但是因为位于坝体的不同部位,又使它们之间存在差异。本文采用FCM对变形测点进行聚类分析,通过对目标函数的优化,得到每个变形测点相对于所有类中心点的隶属度,根据同一簇内的测点相似性尽可能大、不同簇间的测点差异性尽可能大的原则[12],确定变形测点的所属类别,从而达到对坝体分区的目的。
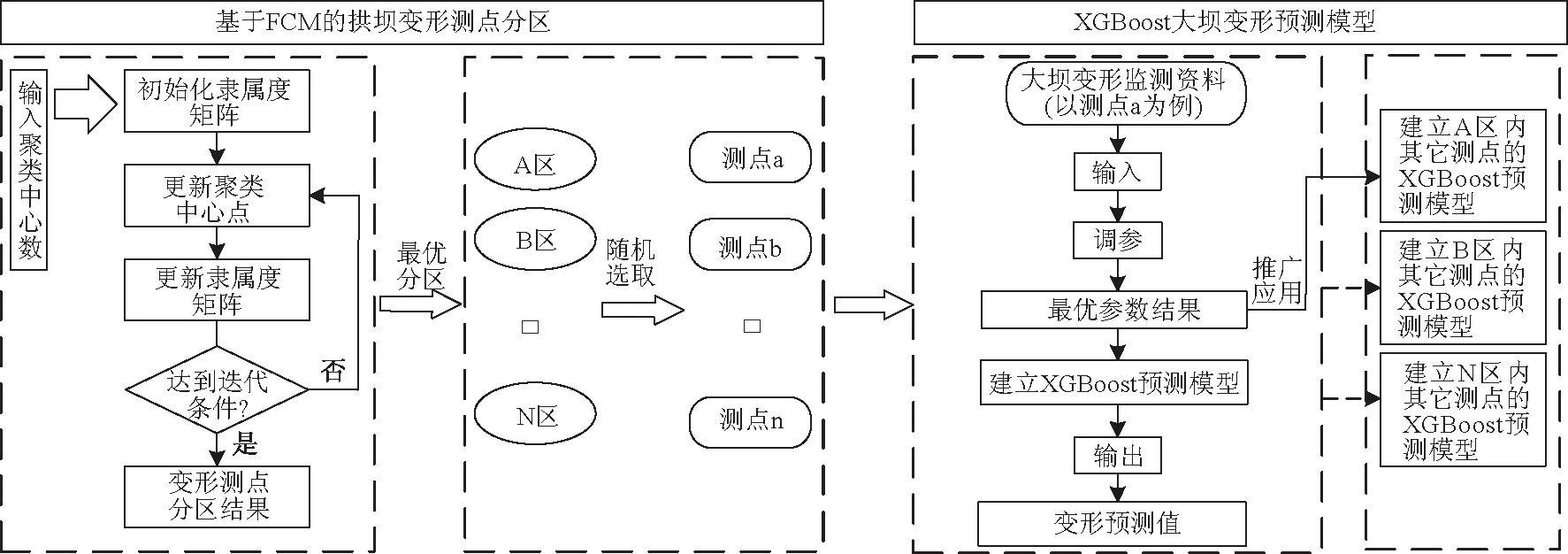
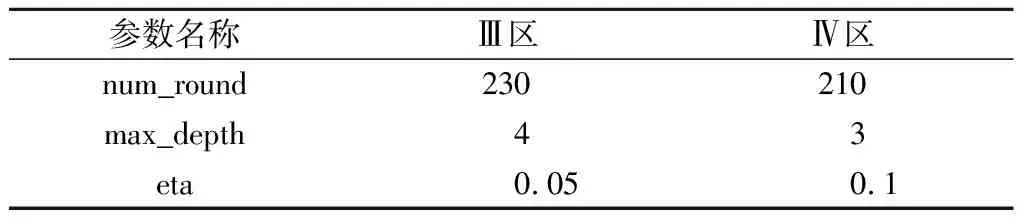
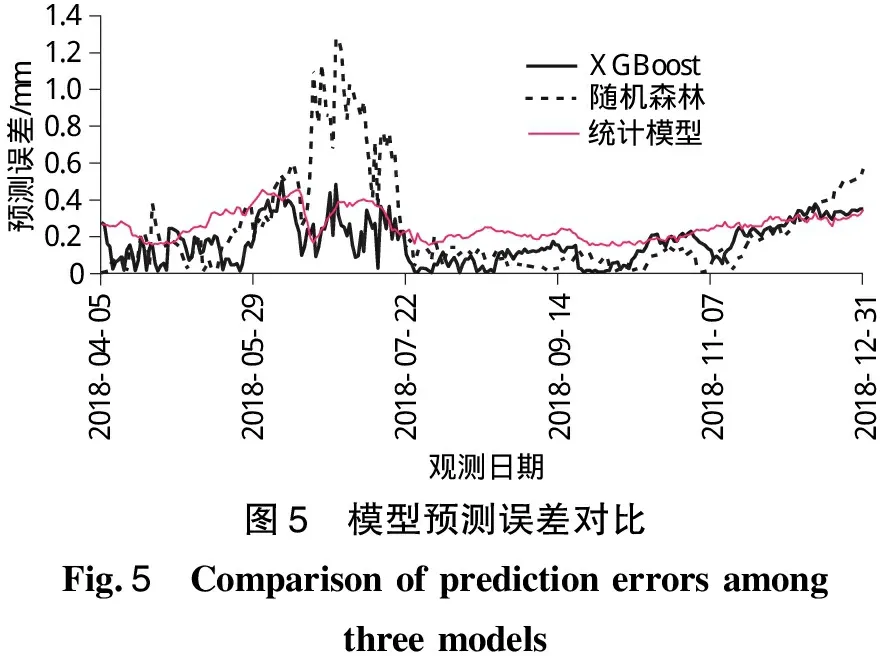
设X={x1,x2,…,xn}为n个变形测点,c为聚类中心数(1 (1) 约束条件为 (2) 大坝变形监测资料数据量大,而且受人为或其他因素影响,常常有数据缺失现象,为了适应上述特征,并以提高建模效率和预测精度为前提,本文引入XGBoost算法建立大坝变形预测模型。XGBoost算法是一种集成学习算法,它的基本思想是通过加入新的弱学习器去拟合前一次弱学习器训练的残差,并在训练结束时得到每个样本的预测分数,最后将所有弱学习器中的预测分数相加即样本的预测值。它是基于梯度提升树(GBDT)的改进算法,主要体现在:①对损失函数由一阶泰勒展开变为二阶,提高了模型的精度;②加入正则项控制模型的复杂度,可以防止过拟合现象;③对特征值缺失的样本,采用稀疏感知算法自动学习它的分裂方向;④支持列抽样,提高了计算速度。 设某变形测点有n个样本,每个样本有m个特征值,将该测点的变形监测资料表示为M={(xi,yi)}(xi∈Rm,yi∈R,i=1,2,…,n)。由于大坝变形预测是回归问题,本文选用回归决策树作为弱学习器,假设样本i在第j棵决策树中叶子节点的分数为ωij,则经t棵决策树迭代后,该样本的预测值表示为 (3) 以3棵决策树为例,求解样本i变形预测值的XGBoost模型示意见图1。 图1 XGBoost模型示意图Fig.1 Flow chart of XGBoost model 图1中虚线框内为回归决策树的简化流程,特征选择及最优切分点有其相应的计算法则(此处不作详述);图1中仅列出了样本i的分数,实际模型中将包含参与训练的所有样本的分数。 为了得到上述模型中样本在每棵树的分数,需要设置一个目标函数,即 (4) 对式(4)中的损失函数进行二阶泰勒展开,则 (5) 在XGBoost模型中,单棵决策树的复杂度表示为 (6) 式中:T为叶子节点的数量;γ为叶子节点数量的惩罚项;ωk为第k个叶子结点的分数;λ是L2正则惩罚项,用来控制泛化误差,防止过拟合。那么t棵决策树组成的复杂度函数表示为 (7) 式中:Ω(ft)是第t棵决策树的复杂度;const表示前t-1棵决策树的复杂度之和,是已知常数。 考虑到常数项对函数的优化不会产生影响,那么在t次迭代后,目标函数简化为 (8) 由式(8)可知,目标函数其实就是关于叶子节点分数的函数,而每个叶子节点的分数都是去拟合上一次训练的残差,因此目标函数的值越小,残差越小,表明求得的预测值越接近样本的真实位移值。 本文以拱坝垂线径向变形监测资料为例,首先利用FCM聚类算法对坝体所有变形测点分区,然后随机选取该分区内某个测点,以该测点为例,建立XGBoost变形预测模型,进而将该参数建立的XGBoost模型推广,应用到所在分区内其他测点的变形预测。模型流程图见图2。 图2 基于FCM-XGBoost的大坝变形预测模型Fig.2 Dam deformation prediction model based on FCM-XGBoost 某混凝土双曲拱坝最大坝高305 m,2012年11月30日正式蓄水。为监测坝体径向位移和切向位移,在5#、9#、11#、13#、16#、19#坝段的1 885、1 829、1 778、1 730、1 664、1 601 m高程上共布置了32个正、倒垂线测点。测点分布见表1。 表1 变形测点分布Table 1 Distribution of deformation measuring points FCM的聚类中心数c需要人为确定,c的取值将直接影响聚类结果的好坏,本文引入轮廓系数S来确定c的最佳取值。单个测点xi的轮廓系数定义为 (9) 式中:a(xi)是xi到所在簇内其他测点的平均距离,表示同一簇内测点的相似度;b(xi)是xi到其最邻近簇内所有测点的平均距离,表示不同簇间测点的离散度。从式(9)可以看出,当轮廓系数S落在[0,1]之间且越接近1时,表示聚类效果越好。 选取2018年8月1日至8月31日期间32个正、倒垂线测点的径向位移作为训练样本的输入值,当聚类中心数c为3~8时的轮廓系数见图3。 图3 不同聚类中心数的轮廓系数Fig.3 Silhouette coefficient of different clustering centroids 由图3可知,当聚类中心数c为5时,聚类效果最好,因此,选取c=5,得到的拱坝变形测点分区结果见表2。 表2 拱坝变形测点分区结果Table 2 Partition results of deformation measuring points for arch dam 由表2可以看出,Ⅳ区内全部为正垂线测点,Ⅲ区内同时包含正垂线测点和倒垂线测点,为了验证不同类型垂线测点的适用性,本文以Ⅲ区内倒垂线测点IP11-1和Ⅳ区内正垂线测点PL13-4为例,选取2012年12月7日至2018年12月31日坝体径向变形监测资料进行研究,其中前80%作为训练集(2012年12月7日至2018年4月4日),后20%作为测试集(2018年4月5日至2018年12月31日)。Ⅲ区及Ⅳ区内所有测点的实测位移过程线见图4。 图4 测点实测位移过程线Fig.4 Process lines of measured displacement at measuring points 由图4可以看出,除少数跳跃点外,分区内所有测点的变形规律基本一致,可以初步判定,聚类对坝体测点分区的结果是有意义的。 4.3.1 模型输入及输出变量的选择 4.3.2 模型的参数调优 模型基于Python3.7的XGBoost库进行,提取不同参数下模型的均方根误差RMSE作为评价指标,均方根误差的计算公式为 (10) 调参结果见表3。其中,num_round是决策树的数量,max_depth是决策树的最大深度,eta是学习率,模型其余参数为默认值。 表3 XGBoost调参结果Table 3 Selection of parameters for XGBoost model 4.3.3 模型的预测结果及推广 将IP11-1测点和PL13-4测点的调参结果分别应用到Ⅲ区和Ⅳ区内其他测点,并建立XGBoost变形预测模型,比较不同测点的相关系数R和均方根误差RMSE,得到预测精度见表4、表5。 表4 Ⅲ区测点预测精度Table 4 Prediction accuracy of measuring points in zone Ⅲ 表5 Ⅳ区测点预测精度Table 5 Prediction accuracy of measuring points in zone Ⅳ 由表4、表5可以看到,测点IP11-1所在的Ⅲ区及测点 PL13-4所在的Ⅳ区内所有测点,R的值均在0.94之上,RMSE的值最高为0.827 36,效果很好,说明在同一分区内的所有测点,因其具有相似的变化规律,可以建立同一预测模型进行分析。 为了检验预测模型对其它分区测点的无效性,本文选取Ⅲ区内的测点PL16-4,建立了在Ⅳ区参数结果下的XGBoost预测模型,得到的R和RMSE结果分别为0.924 02和2.660 46。可以看出,虽然预测结果的相关性较高,但均方根误差表现较差,效果一般,这也说明了对于不同变化规律的测点应分别建模分析。 4.3.4 与随机森林的预测结果对比 本文研究的XGBoost算法是集成学习中Boosting的代表算法,而随机森林是另一种算法Bagging算法的典型代表。目前已有学者将随机森林算法应用在大坝变形预测中,无论在运算时间还是预测精度上,都较传统机器学习算法有很大的进步。因此,本文建立随机森林预测模型与XGBoost模型作对比。 不同于XGBoost模型,建立随机森林预测模型时,必须先对输入变量进行缺失值处理。本文仅以Ⅳ区测点PL13-4为例,首先采取随机森林回归的方式对其输入变量进行缺失值填充,该方式可以保留更多有效信息,然后在此基础上建立随机森林预测模型,调参结果见表6。其中n_estimators是决策树的数量,min_samples_leaf是叶子节点的最少样本量,模型其余参数为默认值。 表6 随机森林调参结果Table 6 Selection of parameters for random forest model XGBoost模型和随机森林模型的调参时间(以决策树的数量这个参数进行一次试算为例)、预测精度对比结果见表7,预测误差对比见图5。 表7 两种模型对比结果Table 7 Comparison of two models 图5 模型预测误差对比Fig.5 Comparison of prediction errors amongthree models 由表7可知,XGBoost模型较随机森林模型,在预测精度上有所提高,而且在运行时间上也表现出了绝对的优势。观察图5可以看到,统计模型的预测误差相对较高,随机森林模型的预测误差在某一时间段出现了突变,说明它在预测过程中不够稳定,而XGBoost模型整体表现平稳,且预测误差始终保持在一个较低值状态。综上,XGBoost算法无论是在预测结果还是建模时间上,都表现得更为优秀。 针对大坝变形中预测效率和预测精度不平衡的问题,基于FCM聚类和XGBoost算法,建立了一种FCM-XGBoost大坝变形预测模型。通过工程实例验证,得出以下结论: (1)将FCM聚类算法应用于拱坝的变形测点分区,解决了测点分别建模的复杂性以及所有测点建立同一模型不准确性的问题,从分区结果来看,该方法具有一定的合理性。 (2)与随机森林模型相比,XGBoost模型不仅在预测精度上表现更好,在时效上也显现出明显的优势,除了能实现缺失值的自动处理,在建模时间上也有很大提升,说明XGBoost算法应用于大坝安全监控领域是有意义的。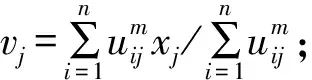
2.2 XGBoost算法


3 基于FCM-XGBoost的大坝变形预测模型
4 实例分析
4.1 工程概况

4.2 基于FCM的拱坝变形测点分区


4.3 XGBoost大坝变形预测模型

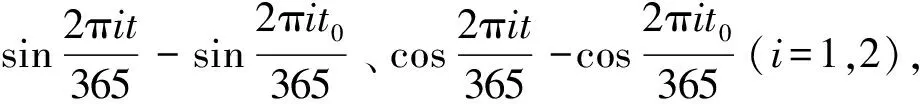
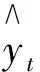




5 结 论
