大型汽车运输船外底板抗屈曲方案分析

郑祖中，王艳春，张新伟，马亚成

（上海船舶研究设计院，上海201203）

0 前 言

汽车运输船是专门为运输成品汽车设计的船舶，可分为纯小型汽车运输船（PCC，Pure Car Carrier）和汽车及卡车混装运输船 （PCTC，Pure Car&Truck Carrier）［1］。 汽车运输船属高附加值船型，降低空船重量意味着可以增加装车量、减小能耗、显著提高船舶整个营运周期的经济效益，因此该类型船舶的结构重量优化备受船东关注。

汽车运输船具有较小的方形系数，在各种装载工况下静水弯矩均为中拱弯矩， 与波浪弯矩叠加后，外底板将承受较大的弯曲压应力［2］。为方便车辆装载，汽车运输船通常设有多层连续甲板，大型汽车运输船连续甲板数量多达十几层。 总的来说，大型汽车运输船的总纵强度较容易满足规范要求，同时外底板剪切应力较小，所以外底板的纵向及剪切屈曲强度通常具有较大的安全裕度，但是大型汽车运输船船宽较大， 使得外底板板架横向跨距较大，在压载工况下将出现显著的横向屈曲问题，因此该类型船舶外底板的板厚及骨材布置主要由板格横向屈曲决定。

外底板抗屈曲方案主要有3 种：增加外板板厚、加密船底纵骨和设置横向屈曲加强筋。 对于横向受压的板格而言，上述3 种加强方案均能有效提高板格的临界屈曲应力。 本文以入级美国船级社（ABS）的某7 500 CEU PCTC 为目标船，建立舱段有限元模型计算外底板板格的横向压应力，结合规范要求详细分析上述3 种加强方案对外底板结构重量的影响，可为将来汽车运输船外底板设计提供参考。

该船的总布置如图1 所示，主尺度参数和入级符号如下：

图1 总布置侧视图

1 双层底布置及规范要求

1.1 双层底布置型式

目标船的双层底布置型式如图2 所示，采用纵骨架式，外底板纵骨与内底板纵骨对齐，纵骨间距为750 mm。 左右舷对称布置。 选取纵骨架式更有利于总纵强度，相对而言，横骨架式双层底需要增设纵桁以减小骨材的横向跨距，且外底板最小板厚要求更厚，不利于重量控制。 布置外底板纵骨时，可考虑外底板纵骨与内底板纵骨对齐或非对齐两种布置方案。 前者结构布置方便，且有利于施工建造；后者减少了外底板设计的限制条件，通过选取合适的纵骨间距可以有效降低结构重量。 两个方案各有优劣，具体设计时需要综合考虑。

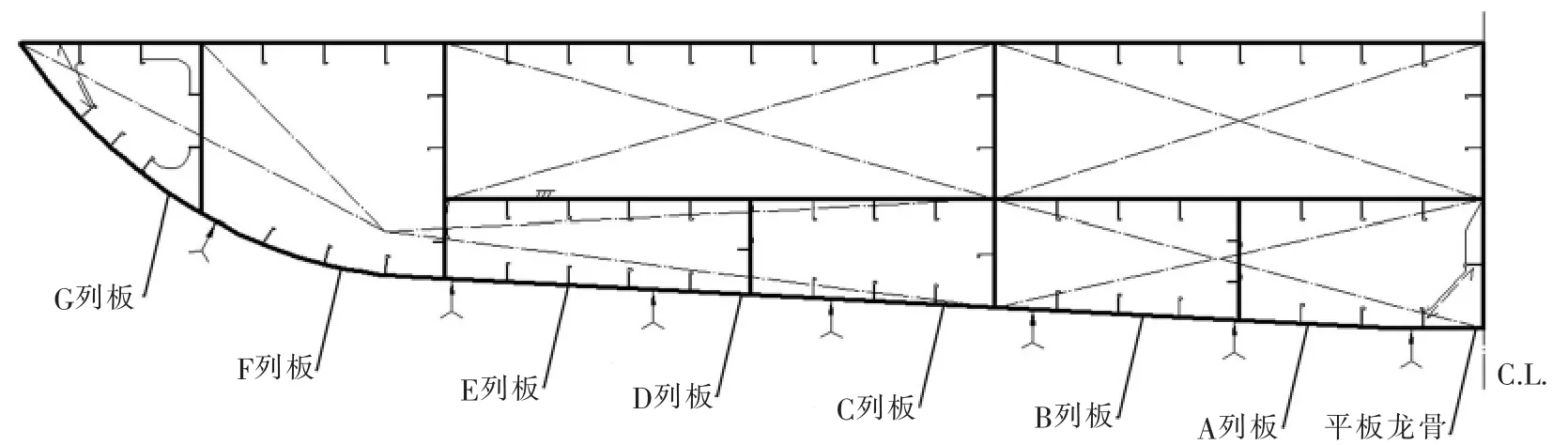
图2 双层底布置型式

目标船外底板由平板龙骨及A～G 列板组成，通常舭部位置外底板的横向压应力较小，G 列板位于舭部且布置了横向加强构件，板格屈曲强度满足要求， 因此仅选取平板龙骨及A～F 列板进行研究，统计和对比分析不同抗屈曲方案下平板龙骨、A～F 列板及其上纵骨和横向加强筋的总重量。 统计外底板结构重量时，纵向范围选取图1 所示机舱前端壁至第1 淡水舱后舱壁，该范围以外的外底板由于采用横骨架式或加密了实肋板，横向屈曲强度满足要求。

1.2 外底板厚度及纵骨尺寸要求

ABS 规范［3］对双层底结构的要求规定了外底板的最小厚度及纵骨最小尺寸，即使外底板的屈曲满足要求，其厚度也不得小于规范规定的最小值。 通过对规范条文进行整理，7 500 CEU PCTC 外底板最小厚度按下式（1）、（2）和（3）计算并取最大值：

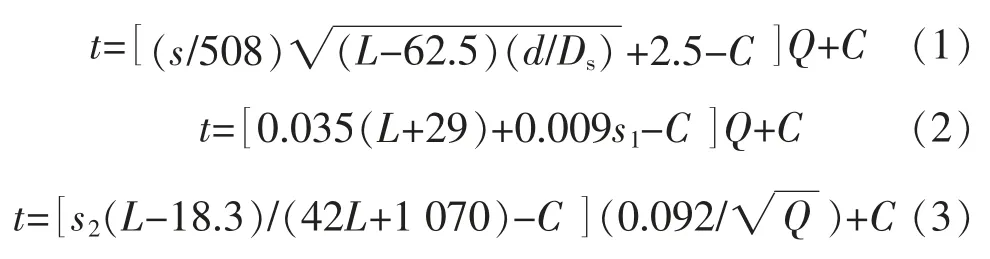
式中：s 为纵骨间距，mm；L 为规范船长，m；d 为吃水，m，不应小于 0.043 3L；Ds为型深，m；s1为规范指定的纵骨间距，610 mm；s2为不小于88%标准间距或 813 mm 之间小者；C 为规范系数，4.3 mm；Q 为材料系数。

此外，平板龙骨的最小厚度应在此基础上增加1.5 mm。 纵骨连同带板的剖面模数不得小于如下公式的计算值：

式中：c 为系数， 无支撑板时取1.3；h 为平板龙骨至载重线距离，或2/3 平板龙骨至水密舱壁最高点或者干舷甲板距离，取大者，m；s 为纵骨间距，m；l 为支撑纵骨实肋板间距，m， 无支撑板时不应小于1.83 m；Q 为材料系数。

经计算，当纵骨间距为750 mm 时，目标船外底板厚度不得小于15.5 mm，平板龙骨最小厚度为17.0 mm。 目标船原始设计方案外底板A-G 列板及平板龙骨的厚度为上述规范要求的最小值，纵骨采用HP280×11 球扁钢以满足上述规范对纵骨剖面模数的要求， 外底板及骨材均采用HT36 高强度钢且尺寸在评估区域内沿船长方向保持一致。

2 有限元模型及计算工况

为了得到外底板板格在设计装载工况下的横向压应力值，按ABS 规范［3］对舱段有限元建模及屈曲分析的要求进行有限元计算。 目标船舱段有限元模型如图3 所示， 模型纵向包含1 个立柱间距，并向前后各延伸1/2 个立柱间距。为提高计算精度，外底板有限元网格进行了细化，如图4 所示，网格大小为 125 mm×133 mm，其余构件采用 s×s 网格。屈曲分析时，外底板需扣除1 mm 腐蚀余量。

图3 舱段有限元模型

图4 外底板网格划分

对于常规的船舶，在压载工况下外底板屈曲通常最恶劣。 大型汽车运输船具有多层全通甲板，在某些特殊的设计装载工况下外底板可能产生更加严重的屈曲问题。 例如除内底板外，其余各层甲板均装载车辆，此时船舶吃水增加，而内底缺少有效的货物压力抵抗海水外压，双层底将出现较大的弯曲变形，导致外底板出现较大的横向压应力。

计算工况如表1 所示，即压载工况及特定设计装载工况，取2 个计算工况下每个列板最大的板格平均横向压应力值， 以满足规范要求为最低标准，得到每种抗屈曲方案下外底板结构的总重量。

表1 计算工况

3 抗屈曲方案

根据ABS 规范［3］计算临界屈曲应力，外底板板格横向临界屈曲应力σc的计算公式如下：

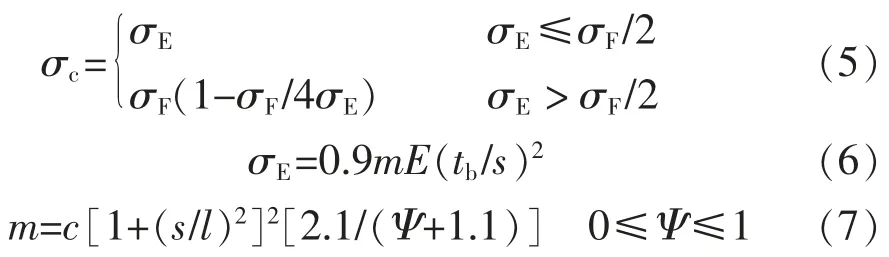
式中：σc为临界屈曲应力，N/mm2；σE为欧拉屈曲应力，N/mm2；σF为材料屈服强度，N/mm2；E 为弹性模量，206 000 N/mm2；tb为板格净厚度，mm；s 为板格短边，mm；l 为板格长边，mm，目标船为 3 200 mm；c 为板格边界为球扁钢时取1.1；Ψ 为板格压应力比值，计算中取1。

3.1 抗屈曲方案1——增加板厚

在原始设计方案的基础上增加外底板板厚，一方面可以提高板格横向临界屈曲应力，另一方面有助于降低板格的横向压应力。 通过有限元分析，得到外底板各列板最大的板格横向压应力值随净板厚的变化情况， 并与板格的临界压应力值进行对比，如图5 所示。

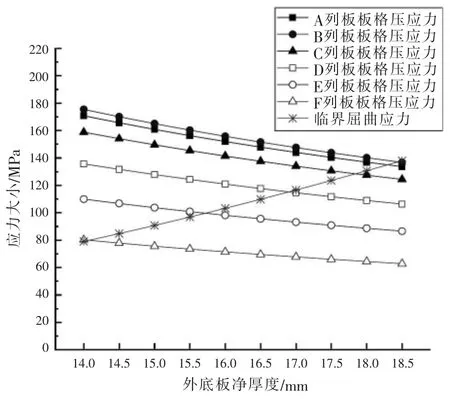
图5 增加板厚方案计算结果

当板格的临界压应力大于最恶劣工况下的横向压应力时，该列板的横向屈曲满足要求。 从图5可以看出，A～F 列板所需的最小净厚度分别为18.5 mm、18.5 mm、18.0 mm、17.0 mm、16.0 mm、14.5 mm。平板龙骨上布置有横向肘板，抗屈曲能力较强， 可取与 A 列板相同的厚度。 纵骨尺寸为HP280×11，满足ABS 规范对纵骨剖面模数的要求。该方案的外底板重量为436 t、 纵骨重量为88 t、外底结构总重量为524 t。

3.2 抗屈曲方案2——加密纵骨

加密纵骨可以减小板格的短边，从临界屈曲应力计算公式可以看出，当板格横向受压时，减小板格短边有助于提高板格临界屈曲应力。 在初始设计方案下，目标船的纵骨间距为750 mm，加密后纵骨间距分别选取625 mm、500 mm、375 mm。 根据ABS规范［3］要求，加密纵骨后外底板最小厚度及骨材尺寸见表2。

表2 外板及纵骨尺寸的规范要求 单位：mm

图6 ～图8 显示了加密纵骨方案的有限元计算结果。 从图 6 可以看出，当纵骨间距为 625 mm 时，A～F列板的净厚度分别取 16.5 mm、16.5 mm、16.0 mm、15.5 mm、14 mm、12.5 mm 即可满足横向屈曲要求。由于规范规定了最小板厚，所以各列板的净厚度不得小于14 mm。 平板龙骨可取与A 列板相同的厚度。 从图7 可以看出，当纵骨间距为500 mm 时，A～F列板的净厚度分别取 14.5 mm、14.5 mm、14.0 mm、13.0 mm、12.5 mm、11.0 mm 即可满足横向屈曲要求。 图8 表明当纵骨间距进一步减小为375 mm 时，从抗屈曲的角度，各列板所需的厚度均小于规范要求的最小板厚，最终各列板的厚度取规范要求的最小值。

图6 加密纵骨方案——（纵骨间距625 mm）

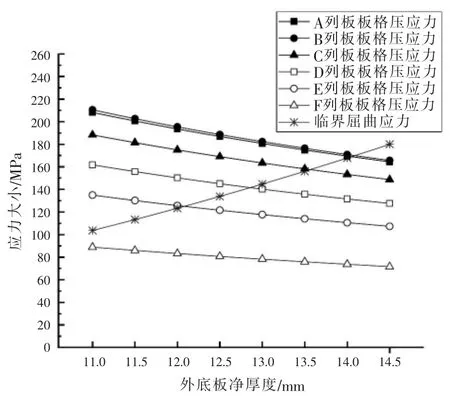
图7 加密纵骨方案——（纵骨间距500 mm）

图8 加密纵骨方案——（纵骨间距375 mm）

该方案对应外底结构总重量见表3。 计算结果表明，随着纵骨间距减小，外底板重量将降低，但受规范最小板厚要求的制约，当纵骨间距进一步减小时，外板底板重量将不再减小，与此同时，加密纵骨将导致纵骨总重量不断增加，因此随着纵骨间距不断减小， 外底结构总重量呈现先减小后增加的趋势。

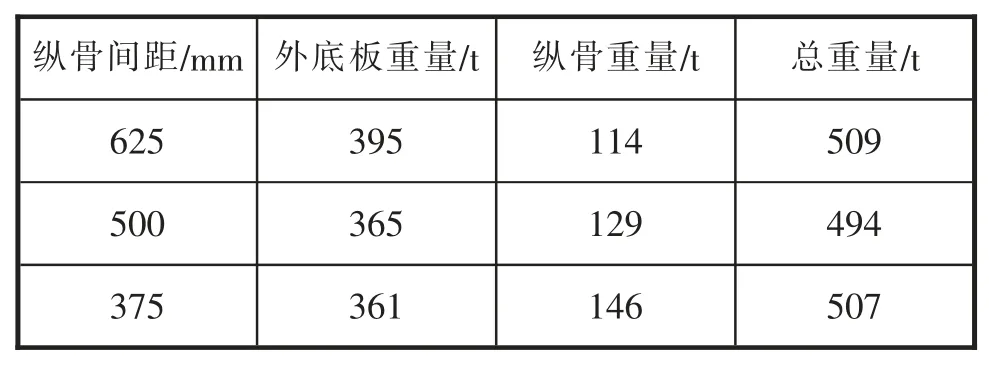
表3 加密纵骨方案外底板结构重量

3.3 抗屈曲方案3——增设横向筋

加横向筋可以减小板格的长边，从临界屈曲应力计算公式可以看出，当板格横向受压时，减小板格长边可以提高板格临界屈曲应力。 一般而言，加横向筋无助于降低板格横向压应力。 7 500 CEU PCTC 每4 个肋位设置1 档强框， 因此分别对板格增加1 根、2 根和3 根横向筋的情况进行分析，横向筋的尺寸取FB150×11。

图9～图11 显示了加横向筋方案的有限元计算结果。 从图9 可以看出，当增加1 根横向筋时，A～F 列板所需的净厚度分别为 17.0 mm、17.0 mm、16.5 mm、15.5 mm、14.5 mm、13 mm。 根据规范最小板厚要求，各列板的净厚度不得小于14.5 mm。 平板龙骨可取与A 列板相同的厚度。 从图10 可以看出，当增加2 根横向筋时，A～F 列板所需的净厚度分别为 14.5 mm、15.0 mm、14.5 mm、13.5 mm、12.5 mm、11.5 mm。图11 表明当增加3 根横向筋时，从抗屈曲的角度，各列板所需的厚度均小于规范要求的最小板厚，最终各列板的厚度取规范要求的最小值。

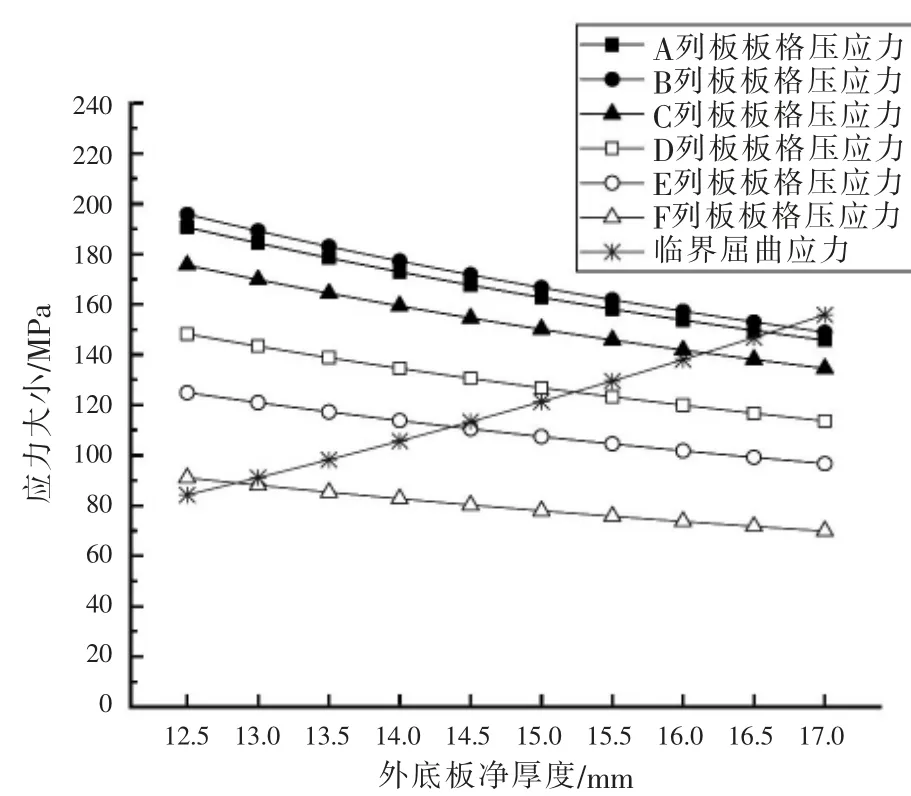
图9 增设横向筋方案——（设1 根横向筋）

图10 增设横向筋方案——（设2 根横向筋）

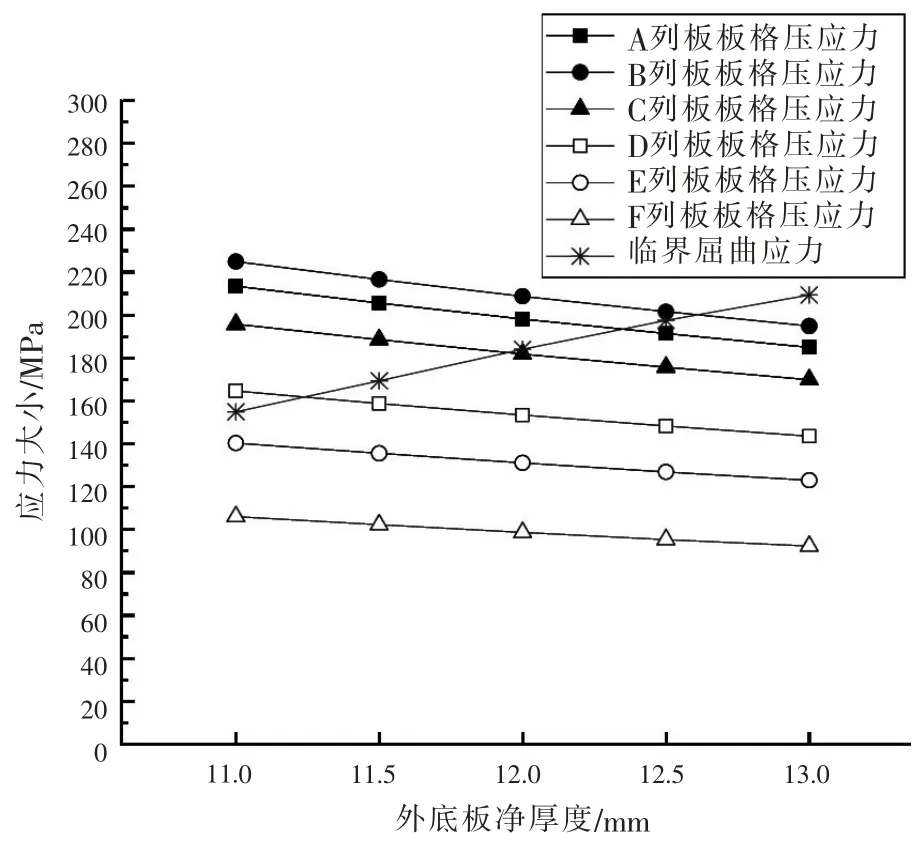
图11 增设横向筋方案——（设3 根横向筋）

该方案对应外底板结构总重量见表4。

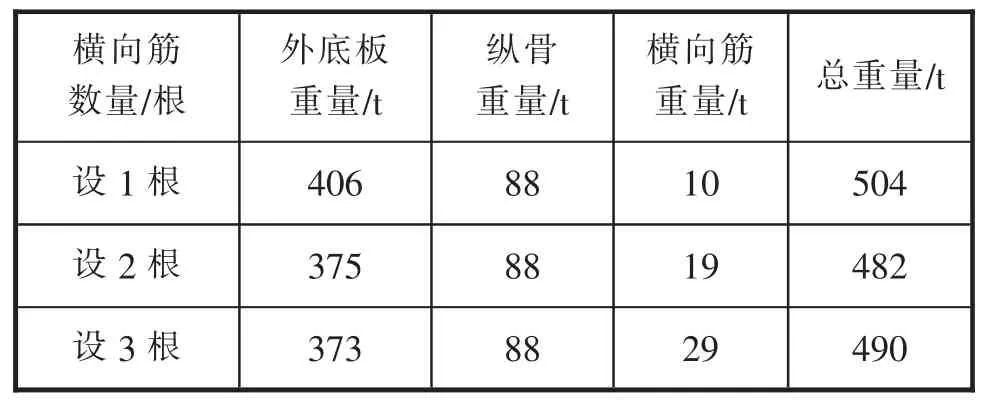
表4 增设横向筋方案外底板结构重量

计算结果表明随着横向筋数量增加，外底板重量将降低，但受规范最小板厚要求的制约，当横向筋数量进一步增加时， 外底板的重量将不再降低，而横向筋重量不断增加， 因此随着横向筋数量增加，外底板结构总重量呈现先减小后增加的趋势。

4 结 语

分析上述3 种抗屈曲方案计算结果，加密纵骨和增设横向筋方案的外底板结构总重量均小于加板厚方案，其中：增设2 根横向筋的方案外底板结构总重量最小， 较加板厚方案可以节省42 t 钢材；当加密纵骨间距为500 mm 时， 该方案相比加板厚方案可以节省30 t 钢材。 因此，从重量的角度，加横向筋方案效果最好，加密纵骨方案次之，加板厚方案重量最大。 对于加密纵骨方案和加横向筋方案，受规范最小板厚要求的制约，随着纵骨间距减小或横向筋数量增加，外底板结构总重量呈现先减小后增加的趋势。

从建造工艺要求的角度，加密纵骨及加横向筋一方面减小了骨材间距而加大焊接难度，另一方面增加了焊缝数量从而增加了建造时的焊接工作量。从营运维护的角度，加横向筋方案容易造成双层底压载舱淤泥堆积，不利于压载舱的清洗和保养，一般不被船东接受。 从船舶稳性的角度，减小外底板结构重量将提高船舶的重心， 不利于船舶的安全性，但也增加了横摇周期，有助于提高船舶的舒适性。 因此，在设计外底结构时，设计人员应结合船舶的实际情况综合考虑， 选取最合适的抗屈曲方案。