一种解决群进化算法参数设置问题的最优向量法

2021-08-11张志强王伟钧

科学技术与工程 2021年18期

张志强，王伟钧，施达

(1.成都大学模式识别与智能信息处理四川省高校重点实验室，成都 610106; 2.成都大学计算机学院，成都 610106)

在很多群进化算法研究中，会设置数值型参数来实现算法搜索的策略。例如，群进化算法如果融入禁忌搜索策略，则会出现控制禁忌表长度的参数；如果群进化算法采用了Memetic进化搜索策略，则会出现控制数据种群个数的参数，因此算法需要设置相关参数值，而设置不同的参数值，则会影响算法搜索的效率。由此看见，为了能够解决群进化算法参数设置问题，需要设计有效的参数值设定方法。

目前有文献针对启发式算法参数的设置做了相应的研究。文献[1-3]根据算法特点和参数设置的经验相结合，对算法的参数进行了设定，并利用设定的参数值进行了算法的测试。文献[4-11]根据算法特点设置了多个参数预设值，并利用设定的参数预设值进行算法的测试，并根据测试结果进行数据分析，从而确定最好参数值。文献[12]根据算法特点设置了多个参数预设值，并根据获取的部分样本数据采用统计最优值个数大小的判定规则来确定参数值。文献[13]提出了利用参数分析方法工具(irace)来确定算法参数的策略。文献[14]提出了对算法参数进行方差分析来确定算法参数的策略。

虽然对于启发式算法的参数设置方法已有相关文献进行了研究，但有些方法实现比较复杂，需要利用工具进行分析，而有些方法实现又过于简单，依据经验来直接设置参数值。从基于复杂性和有效性方面进行考虑，提出新的有效算法参数设置方法对解决参数设置问题的研究具有重要的意义。为此，以群进化算法搜索结果的样本数据为基础，提出一种算法参数设置的最优向量法，将样本数据转换为向量进行计算，依据向量计算的判定规则进行最优参数值的确定，以期为群进化算法中参数设置的优化提供参考。

1 常规统计方法

当群进化算法进行参数设置时，通常情况下可以设置多个参数值进行算法调优，以获取最优参数值。最优参数值的确定一般可以采用常规统计方法来实现，该方法的实现过程如下所示。

第一步，首先根据群进化算法H的参数结构，结合问题的求解需求，预设n组参数值集合P= {P1，P2， …，Pi，…，Pn}，其中Pi表示预设的第i组参数值。

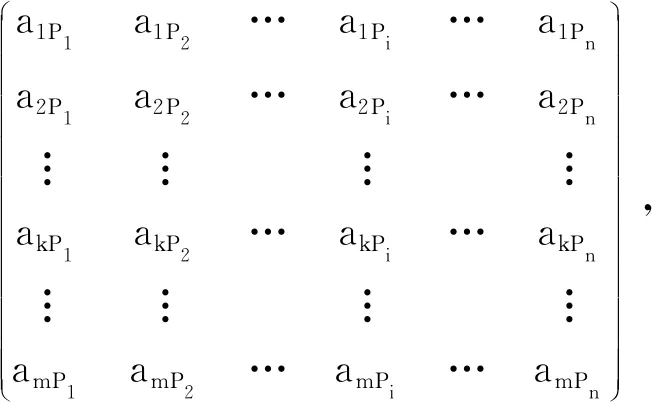
第二步，采用群进化算法H对m个测试用例图进行搜索测试，获得一批测试结果的样本数据。当群进化算法参数采用了第i(1 ≤i≤n)组参数值，对m个测试用例图进行搜索测试后，会获得一个由m个测试结果样本数据构成的向量APi，即:APi= (a1Pi，a2Pi，…，akPi，…，amPi)T(1 ≤i≤n，1≤k≤m)。

由此可见，最终获得的测试结果样本数据由向量组A构成，这里A= {AP1，AP2，…，APi，…，APn}，向量组A用二维向量矩阵表示为

1≤i≤n， 1≤k≤m

(1)

式(1)中:akPi为利用第i组参数值Pi设置的群进化算法对第k个测试用例图进行搜索的结果数据；n为参数值的组数；m为测试用例图个数。

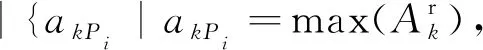
1≤i≤n， 1≤k≤m}|

(2)

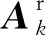
统计最小值数据元素个数为

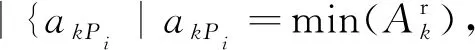
1≤i≤n， 1≤k≤m}|

(3)

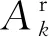
这里统计最大值或最小值则需要根据群进化算法解决的问题需求来确定。

第四步，根据统计出的nbsi的值，确定最优参数值为

(4)

式(4)中:nbsx为n个nbsi值中的最大值；x为取最大值时所对应A的列向量序号；Px为对应的第x组参数值；Popt为最优的第opt组参数值。

从式(4)可以看出，最优参数值确定的原则是以统计的样本数据最好值个数为依据。

2 最优向量法

从常规统计方法可以看出，该方法虽然可以根据样本数据进行最优参数值的确定。但该方法有一些缺点。

(1)当统计的nbsx有多个相同值时，这时无法准确判断在多个相同值中选择哪个值作为最优参数值来设置群进化算法，使得其搜索能力相对最强。

(2)采用常规统计方法只能依据最值(根据问题的定义采用最大值或最小值)来判定参数的最优值，根据最值在有限样本数据量中进行判定不一定能找到最优向量值，从而也就不一定能找到最优参数值。

为此，提出了最优向量法来解决这些问题。最优向量法的主要思想是依据群进化算法的参数结构，利用第1节方法获取向量组A，以此构建有限样本数据，再以有限样本数据量为基础采用向量计算方式来准确判定样本数据中的最优向量，从而确定最优参数值。

2.1 向量的标准化处理

在最优向量法中，首先对每个向量进行标准化处理，这样使得在计算向量的长度和向量间的夹角时能保证所有需要处理的向量都在同一个象限中。

(5)

如果样本数据中数据值越小表示结果值越优，则采用的转换形式为

(6)

式(6)中:a′kPi为对akPi标准化处理后的结果；A″为转换后的向量组。

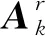
如果以式(5)进行标准化处理后，A″中所有数据值都在[0，1]范围内，A″中所有列向量的方向都在第一象限；如果以式(6)进行标准化处理后，A″中所有数据值都在[-1，0]范围内，A″中所有列向量的方向都在第三象限。

2.2 向量的长度计算

为了在有限的样本数据中准确找到最优列向量，从而找到产生该最优列向量样本数据所对应的参数值作为最优参数值，将针对前面已完成标准化处理的样本数据向量组A″，计算每个列向量的长度，即计算列向量的模。向量组A″中每个列向量长度计算过程为

1≤i≤n

(7)

式(7)中:A″Pi为A″中第i个列向量；‖A″Pi‖为列向量长度。

再计算所有列向量的长度后，找出长度值最大的列向量A″Px，则A″Px为最优向量法中找到的最优列向量，产生该列向量样本数据所对应的参数值为最优参数值Popt，该过程为

(8)

式(8)中:A″Px为长度值最大的第x个列向量；x为取最大值时所对应A″的列向量序号。

2.3 向量间的夹角度计算

在计算列向量A″Pi的长度时，如果出现多个最大长度值相同的列向量，从多个相同值的列向量中找出最优列向量则可以通过计算向量间的夹角度进行判定。

首先在向量组A″找出理想列向量A″Pideal，理想列向量A″Pideal是由向量组A″中每个行向量中其分量的最大值或者最小值构成(这里采用最大值或最小值由求解问题的描述来决定)。由于向量组A″是经过标准化处理的，因此，根据求解问题的描述，如果在样本数据中取最大值为最好值，则采用式(5)进行标准化处理，这时理想列向量A″Pideal= (1，1，…，1)T， |A″Pideal| =m；如果在样本数据中取最小值为最优值，则采用式(6)进行标准化处理，这时理想列向量A″Pideal=(-1，-1，…，-1)T， |A″Pideal| =m。

当理想列向量确定后，依次从多个相同最大向量长度值的列向量集合S中获取每个A″Pu(1 ≤u≤ |S|)，计算A″Pu与A″Pideal的夹角度进行判断，如果夹角度越小，表明该向量越靠近理想向量，最优向量法认为该向量越优。如果理想列向量A″Pideal= (1，1，…，1)T，则夹角度变化如图1所示；如果理想列向量A″Pideal=(-1，-1，…， -1)T，则夹角度变化如图2所示。在图1中可以看出，当θ1<θ2，则cosθ1> cosθ2，说明向量1比向量2更靠近理想向量，最优向量法认为向量1比向量2更优。在图2中，当θ1<θ2，则cosθ1> cosθ2，说明向量1比向量2更靠近理想向量，最优向量法认为向量1比向量2更优。

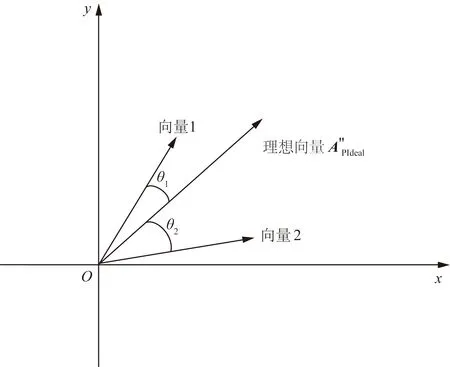
图1 第一象限的向量间夹角度变化情况

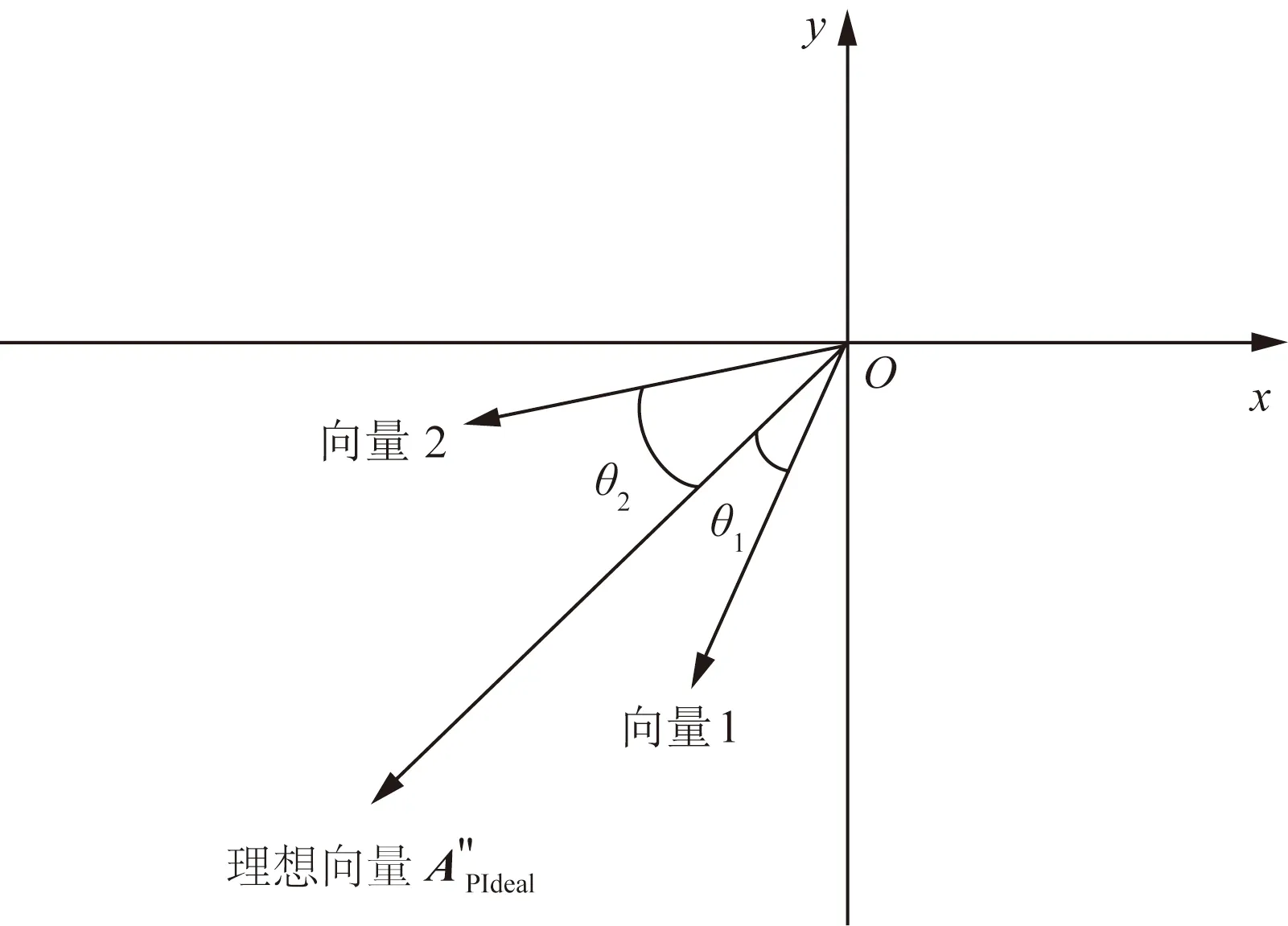
图2 第三象限的向量间夹角度变化情况

产生最优列向量A″Py以及对应的最优参数值Popt为

(9)

式(9)中:S为最大向量长度值的列向量集合；A″Pu为最大长度值的列向量；θu为向量A″Pideal和A″Pu间的夹角度；A″Py为与向量A″Pideal间夹角度最小的第y个列向量；y为取最小夹角度时所对应A″的列向量序号。

2.4 最优向量法的实现流程

最优向量法的实现流程如图3所示。从图3中可以看出，当最大长度值的向量有多个时，则进入向量间夹角度值的计算判定过程，当与理想向量夹角度最小的向量有多个时，则可认为最优向量有多个，这时可以从它们中随机选择一个作为最优向量。一般来说，通过向量长度计算和向量间的夹角度计算两个阶段的判定基本上都能找出唯一的最优向量，从而确定出最优参数值。

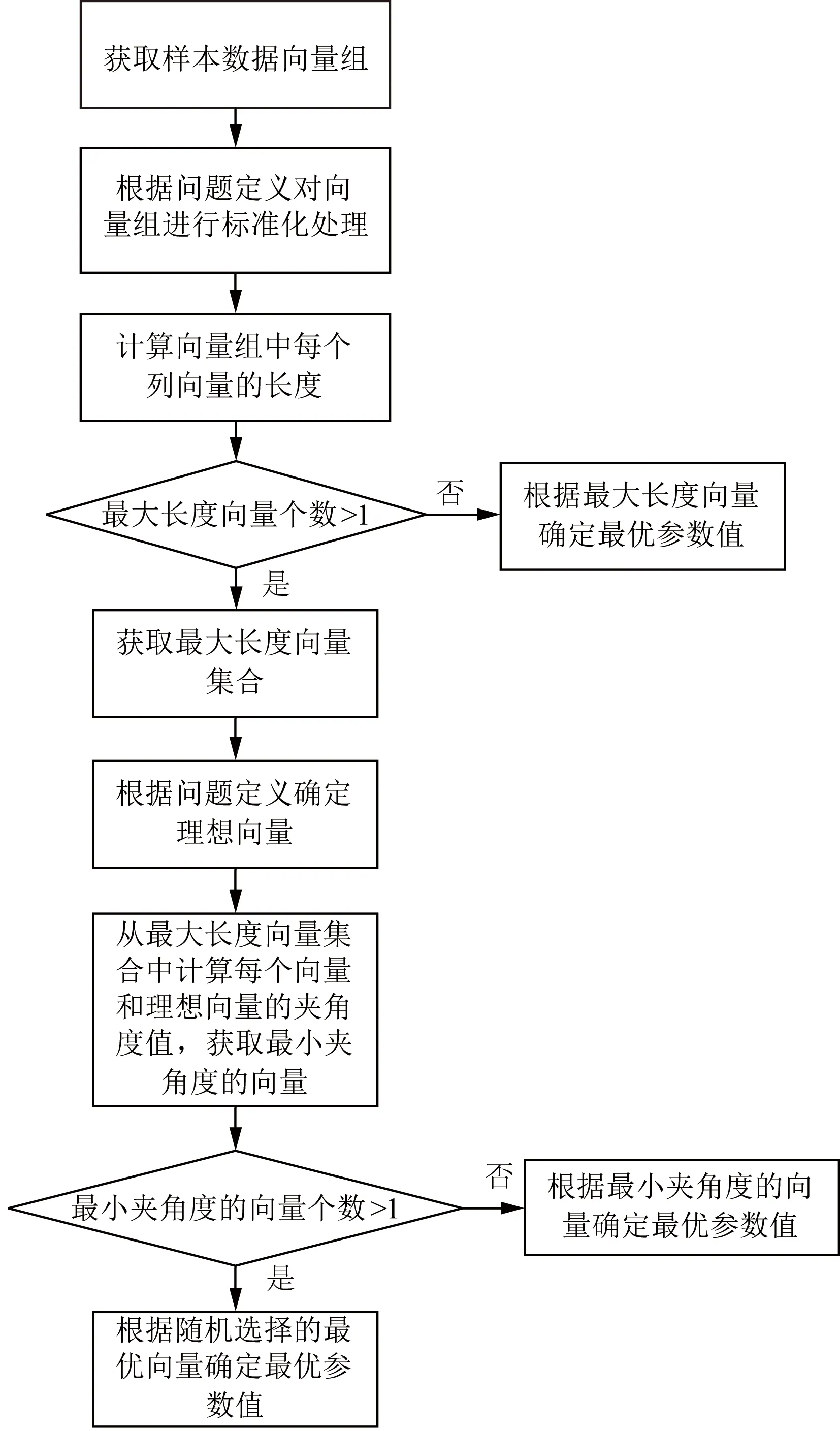
图3 最优向量法的实现流程

3 实验分析

最优向量法采用Java编程实现，测试环境为Windows7(64 bit)、CPU为Intel Pentium(R) G630 (2.7 GHz)、内存为8 GB。

3.1 求解问题的描述

进行最优向量法验证的求解问题采用图论的黑白着色问题(black and white coloring problem， BWC)，该问题被文献[15]提出并证明为NP(non-deterministic polynomial)难问题。在文献[15]中该问题主要描述为给定一个图G= (V，E)，其中V为图G的顶点集，E为图G的边集，对图G的顶点进行黑白着色，将集合V分割为B和W两个顶点集，其中，B为着黑色的顶点集，W为着白色的顶点集，图G中没有跨越集合B和集合W中顶点的边，即图G中每条边关联的两个顶点不能分别是B和W中的顶点，当集合B中的顶点个数确定后，则|W|的最大值是问题的最优解。

3.2 实验结果分析

根据求解问题的描述，设计了基于Memetic思想的群进化算法搜索BWC问题解，群进化算法中设置了禁忌表长度L和数据种群个数d作为参数。首先设定参数d和L的预设值(d，L)，这里d和L的取值范围分别为{4， 8， 12， 16}和{10， 60， 90， 200}，可见参数预设值有16种，即P= {(4，10)， (4，60)， (4，90)， (4，200)， (8，10)， (8，60)， (8，90)， (8，200)， (12，10)， (12，60)， (12，90)， (12，200)， (16，10)， (16，60)， (16，90)， (16，200)}，n= 16。

利用群进化算法对第一组benchmark图进行搜索测试，当每种参数预设值确定后，每个benchmark图测试20次，每次测试30 min，由此，获得的搜索结果如表1所示。这里为了更准确地分析出群进化算法在不同参数中的搜索能力，采用搜索结果的平均值作为样本数据源进行最优向量法的分析。

表1 群进化算法对第一组benchmark图的搜索结果

以表1数据为样本数据，根据常规统计方法策略利用式(2)发现nbs1=2、nbs3=2并且最大，由此根据式(4)准确判断最优参数预设值比较困难。

为了克服常规统计方法策略的缺点，采用最优向量法来处理样本数据。根据表1样本数据得到向量组A；对向量组A利用式(5)(根据BWC问题描述，样本数据中选择最大值为最好值)进行向量标准化处理后得到向量组A″。

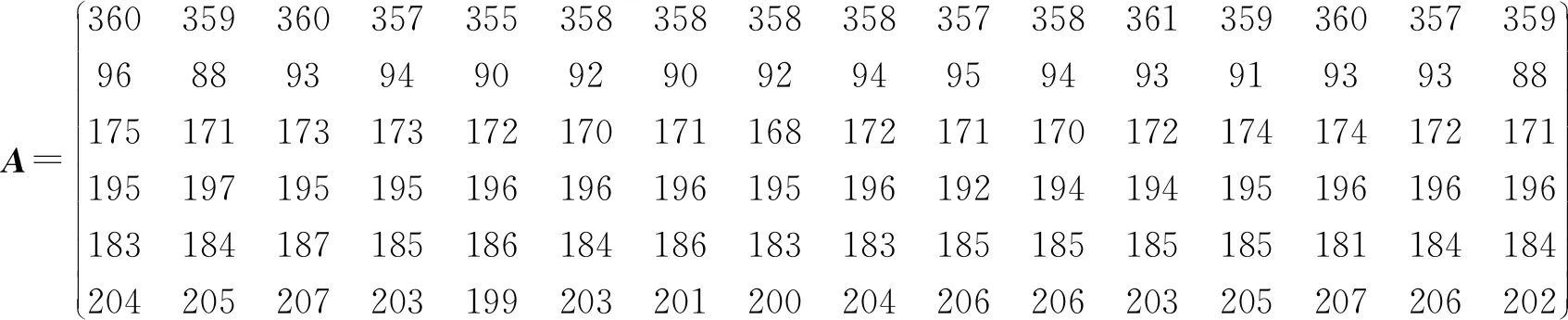
根据式(7)计算A″中每个列向量长度值为{1.9， 1.6， 2.0， 1.5， 1.3， 1.3， 1.4， 1.0， 1.5， 1.5， 1.5， 1.6， 1.6， 1.9， 1.6， 1.3}，在这组数据中，列向量A″P3的长度值最大，即||A″P3|| = 2.0，利用式(8)得到A″Px=A″P3，则Popt=Px=P3，采用最优向量法确定的最优参数值组合为{d= 4，L= 90}。如果有多个列向量长度最大值相同时，则按照第2.3节的式(9)进行向量间夹角度的计算来进一步判定。

利用群进化算法对第二组benchmark图进行搜索测试，当每种参数预设值确定后，每个benchmark图测试20次，每次测试30 min，由此获得的搜索结果如表2所示。

根据表2的数据，不同参数值的群进化算法搜索结果中Best最大值个数和Avg最大值个数统计情况如表3所示。

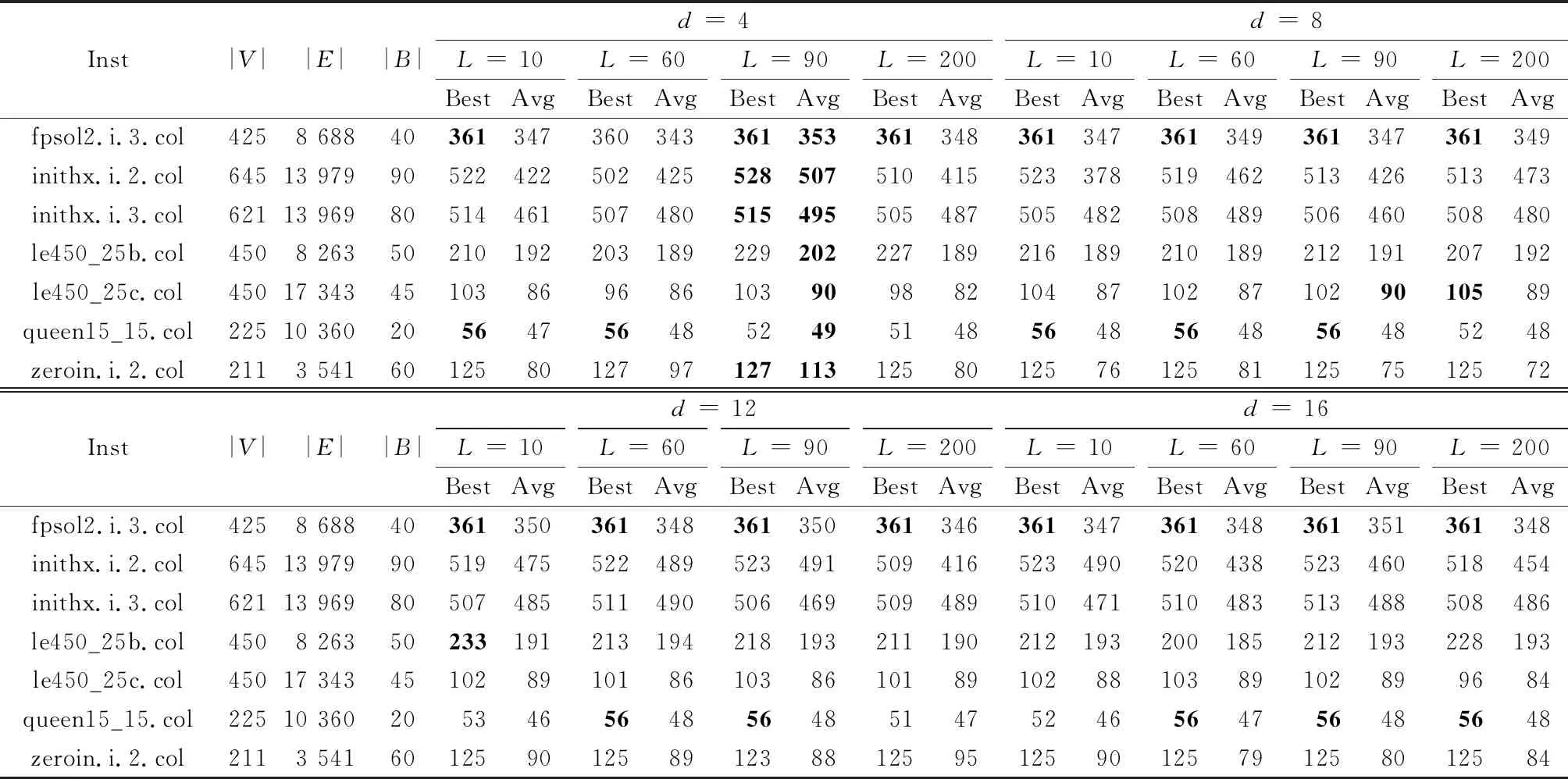
表2 群进化算法对第二组benchmark图的搜索结果

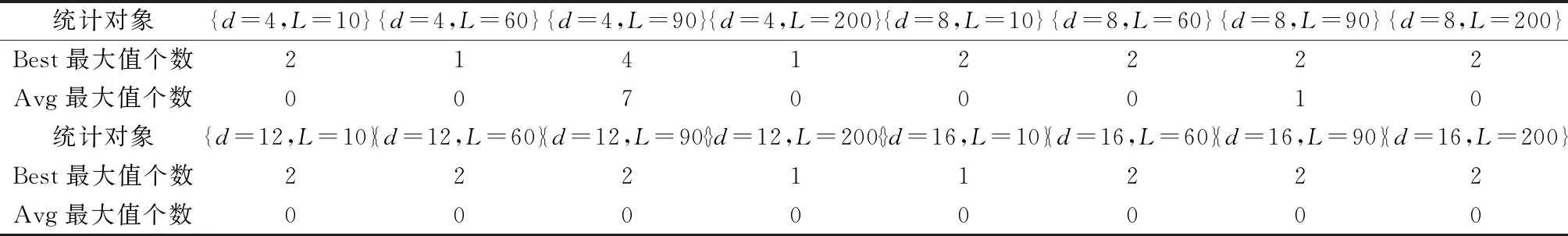
表3 搜索结果中最大值个数的统计(表2数据)

在表3中，利用最优向量法找出的参数值{d= 4，L= 90}设定的群进化算法搜索的Best最大值个数为4，Avg最大值个数为7，其算法搜索能力相对最强。

利用群进化算法对第三组benchmark图进行搜索测试，当每种参数预设值确定后，每个图测试10次，每次测试30 min，由此获得的搜索结果如表4所示。

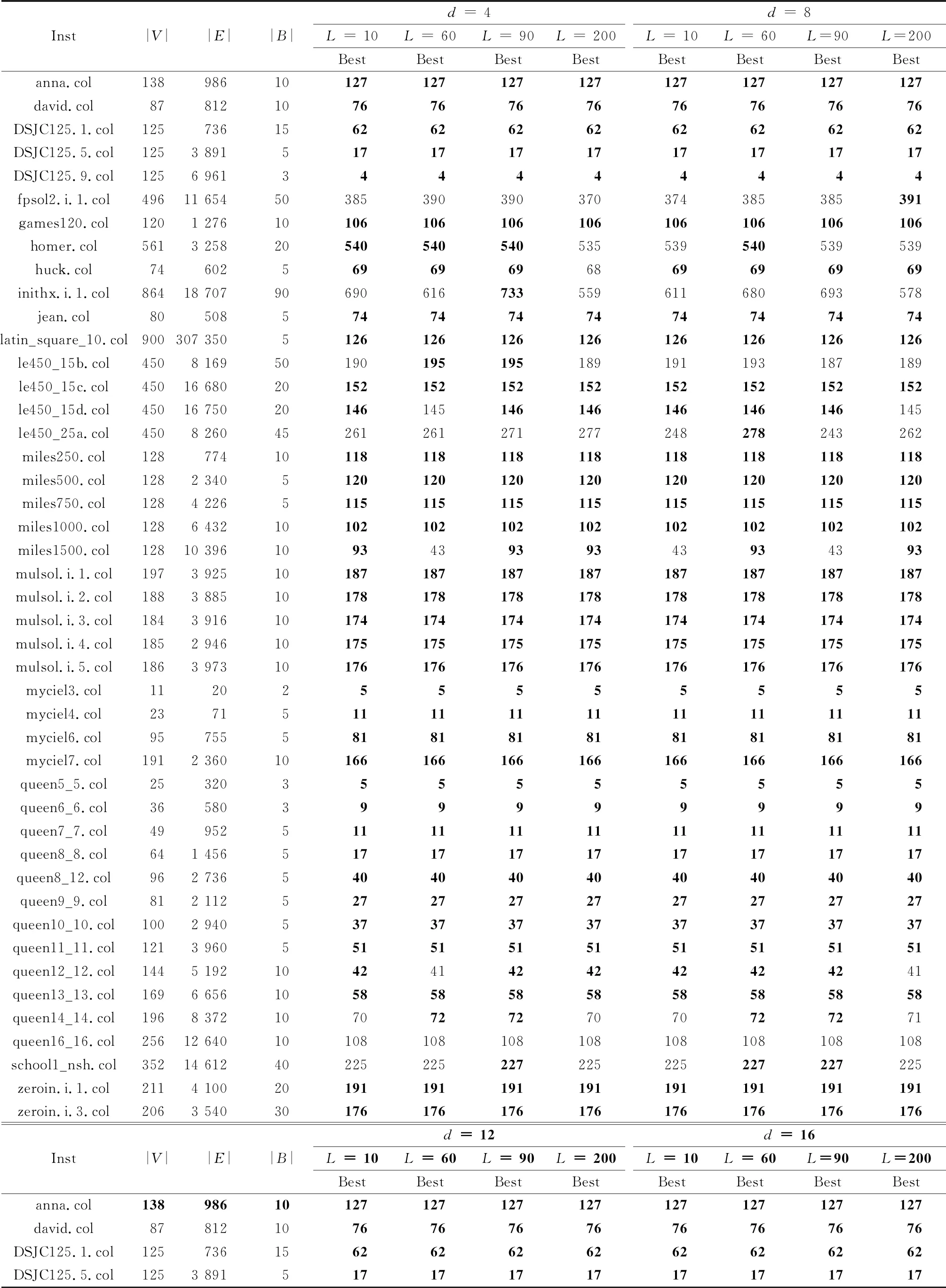
表4 群进化算法对第三组benchmark图的搜索结果

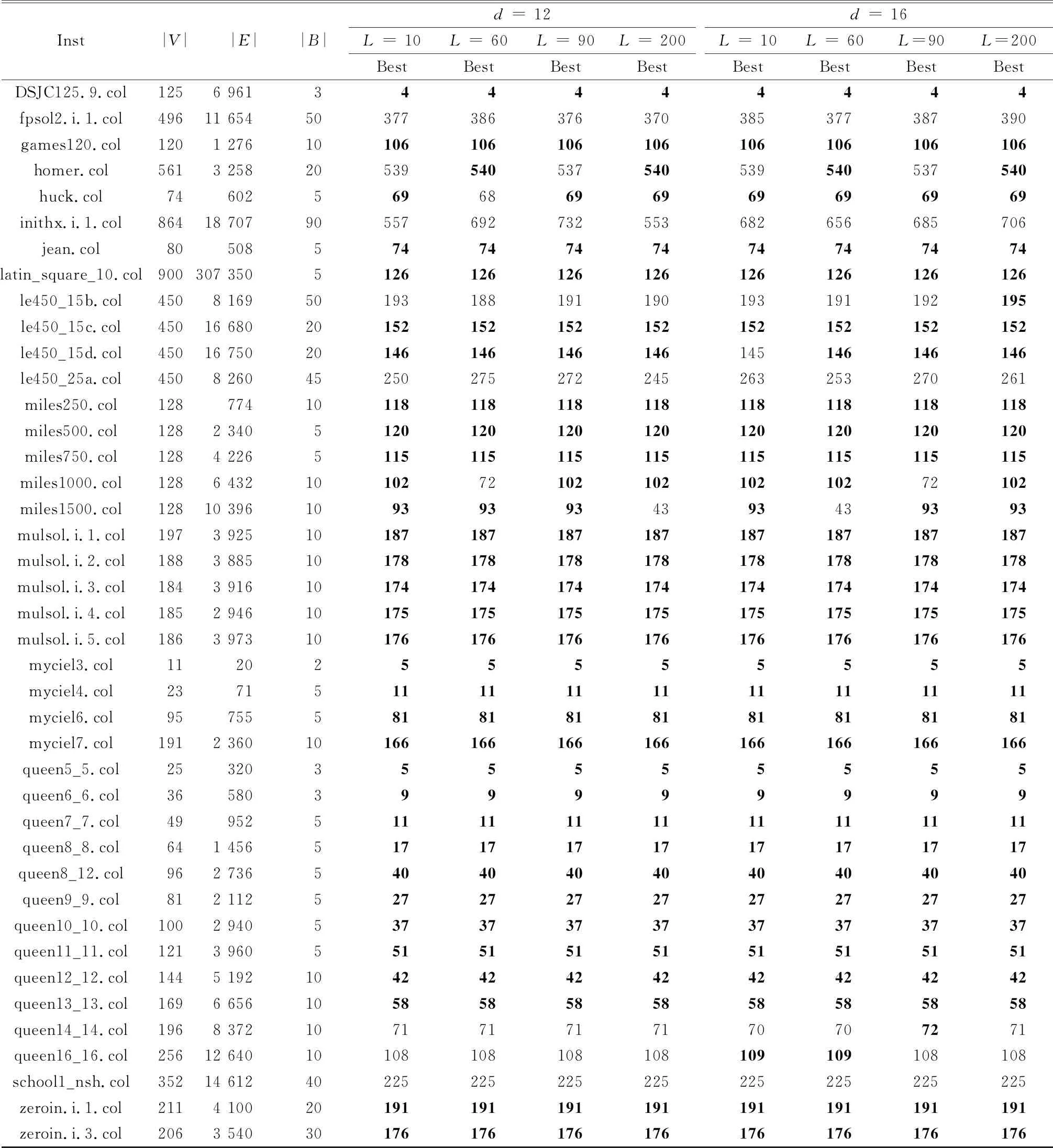
续表

根据表4的数据进行统计，统计结果如表5所示。从表5可以看出，根据表1测试的结果利用最优向量法确定的最优参数值组合{d= 4，L= 90}来设置群进化算法，其能发现42个测试图的最大值，能发现的最好值个数最多，其搜索能力相对最强。

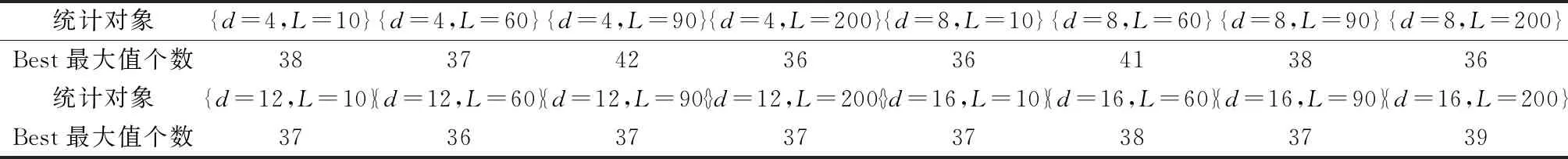
表5 搜索结果中最大值个数的统计(表4数据)

由此可见，针对获取的样本数据，可以利用最优向量法对样本数据进行处理，从而比较准确地确定最优参数值。

3.3 与其他文献算法的比较分析

为了验证最优向量法对已有文献提出的群进化算法参数设置的有效性，在实验中，将最优向量法应用到文献[16]提出的群进化算法的参数设置中进行测试。

文献[16]提出了一种Memetic群进化算法(算法名:Memetic_D_O_MLCP)来解决最小负载着色问题(minimum load coloring problem，MLCP)，该问题已被其他文献证明为NP难问题。文献[16]提出的Memetic算法的参数设置方式是根据文献[16]中表1的样本数据采用常规统计方法确定，其算法参数被确定为{p= 12，L= 90}；而根据文献[16]中表1的样本数据(以Avg数据为处理对象)，采用最优向量法策略(文献[16]提出了值越大结果越优的判定规则)，根据式(7)计算A″中每个列向量长度值为{2.05， 2.12， 2.36， 1.72， 2.04， 2.23， 2.08， 1.86， 1.81}，列向量A″P3的长度值最大，即||A″P3|| = 2.36，利用式(8)得到A″Px=A″P3，则Popt=Px=P3，采用最优向量法确定的最优参数值组合为{p= 4，L= 90}。这里参数变量p和L均为文献[16]提出的参数变量(p为数据种群个数，L为禁忌表长度)。将参数{p= 4，L= 90}设置到Memetic算法中，并利用文献[16]提出的59个benchmark图例进行算法测试(每个图测试20次，每次测试30 min，与文献[16]的实验条件一致)。获得的测试结果如表6所示。

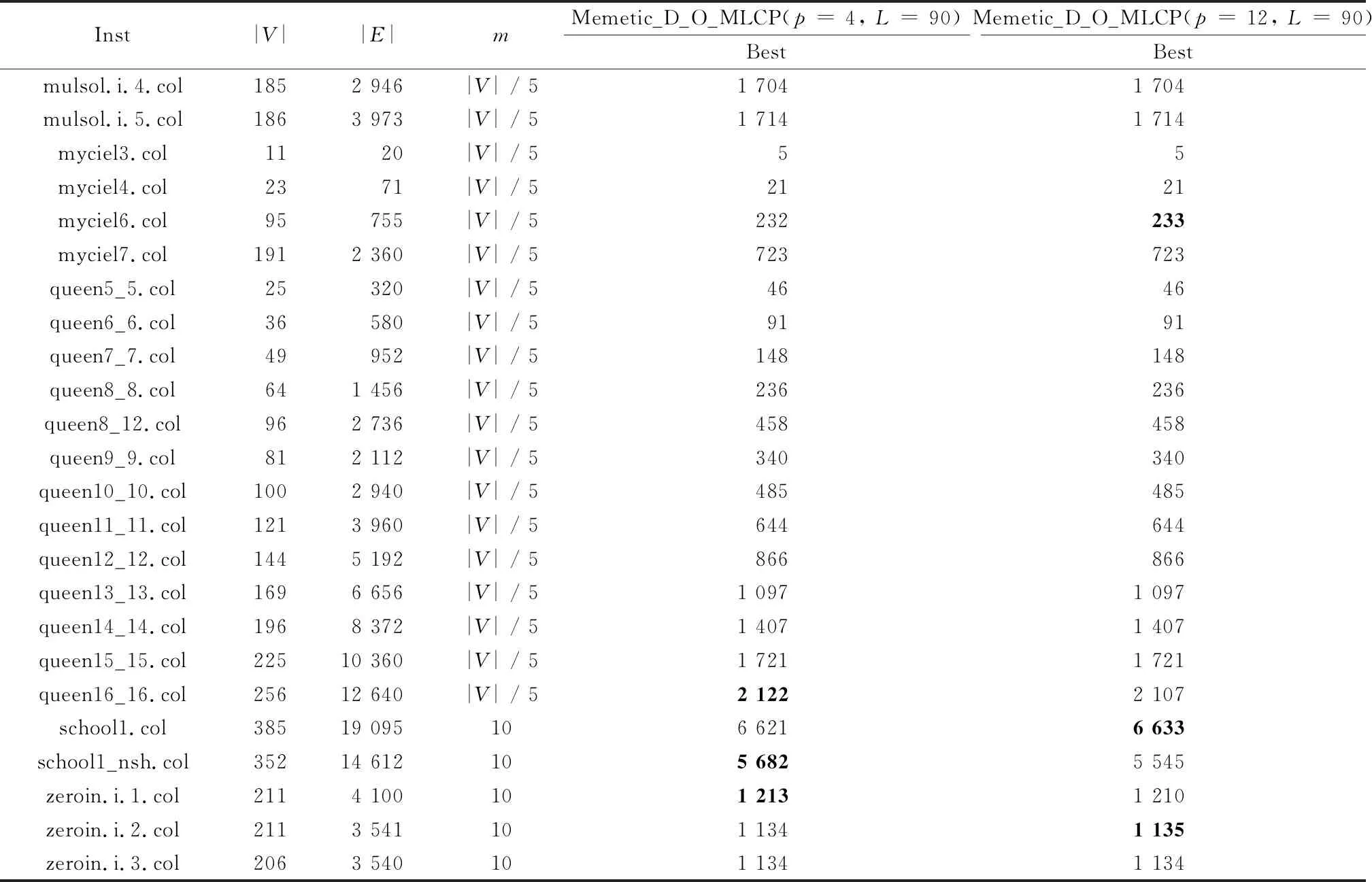
在表6中，m表示文献[16]benchmark图中着红色的顶点初始个数；Memetic_D_O_MLCP (p=4，L=90)代表利用最优向量法设置参数的Memetic算法；Memetic_D_O_MLCP (p=12，L=90)代表文献[16]中利用常规统计方法设置参数的Memetic算法；Best表示Memetic算法能够搜索到的MLCP解决方案的最好值，最好值用加粗表示。

表6 Memetic_D_O_MLCP(p=4，L=90)与Memetic_D_O_MLCP(p=12，L=90)的比较结果

续表

从表6的结果分析发现，在59个benchmark图例中，利用最优向量法确定参数设置的Memetic算法能够搜索到46个图例的最好值，利用文献[16]提出的常规统计方法确定参数设置的Memetic算法能够搜索到43个图例的最好值，其中两个算法有30个图例的搜索结果相同，由此看见，本文算法能够搜索到的最好值个数比文献[16]算法搜索到的最好值个数多。另外，本文算法搜索结果中有16个图例的最好值比文献[16]算法的结果好，从而改进了文献[16]中16个图例的最好值结果。