基于室内高光谱数据的多种类型土壤有机质估算模型比较

郄 欣，齐雁冰，刘姣姣，王 珂，陈敏辉

(西北农林科技大学资源环境学院，陕西 杨凌 712100)

土壤有机质作为土壤固相的重要组成部分，不仅是土壤肥力的保证，也是维持大气碳平衡的重要指标[1]。快速准确地获取田间土壤理化信息是实现现代精细农业的基本需求，对于充分发挥土壤生产潜力，实现农业高产、优质、高效协调发展以及保障农业生态安全都具有重要意义。传统室内测定土壤有机质含量的化学方法程序繁琐、耗时耗力，处理不当还会造成一定的环境污染[2]。相比传统的研究方法，高光谱技术则具有省时省力、无污染、无破坏等优点[3]，在预测有机质方面极具优势和潜力。高光谱数据具有光谱分辨率高、波段连续性强、空间分辨率低等特点，可以直接在野外或田间进行光谱数据采集，不仅节省了大量的人力和物力，还能与大尺度遥感影像或航摄相片相结合，实现成像光谱土壤属性填图，为大面积、简便采集土壤属性数据提供了可行性，成为目前获取土壤属性信息的重要手段，已被广泛应用于土壤资源调查、分类、评价、制图等方面[4]。

基于高光谱的土壤有机质(碳)估算已经成为近年来土壤遥感的重要研究内容，而所构建的估算模型的精度取决于光谱变换[5]和敏感波段提取[6]两个方面。为较好地消除土壤光谱曲线噪音、背景等影响，变非线性关系为线性关系，常对原始光谱进行数学变换，目前主要变换形式有平滑处理、导数变换、归一化处理、多元散射校正、标准正态化、包络线去除等[7-9]。不同的土壤类型和土壤有机质含量会在可见光至近红外区域内产生不同的响应波段。近年来，国内外学者通过研究不同类型土壤有机质含量与光谱反射率的相关性，发现他们具有显著负相关关系，但对于土壤有机质响应波段的提取并不一致。Galvao等[10]在室内研究证实了土壤反射光谱在550～700 nm处的吸收峰主要是由有机质引起，而且是非线性关系；史舟等[7]研究发现，土壤有机质含量与一阶微分光谱曲线相关系数较高的波段为580、820、1 400 nm和 2200 nm；彭杰等[11]在通过室内土壤有机质人工处理条件下发现土壤有机质含量与可见光波段的反射率具有较强的相关性，决定系数(R2)最大为0.7902；Gunsaulis等[12]研究表明，土壤有机质含量与红光波段的反射率具有较强的相关性，决定系数(R2)可达0.609；纪文君等[13]研究了浙江、河南、四川、黑龙江4个地区不同类型的土壤样品，对比得出600～800 nm波段可作为研究区域内不同土壤共同的有机质光谱响应波段。

随着高光谱技术的推广应用，国内外基于高光谱数据建立的土壤有机质估算模型均取得了较为显著的预测效果，但在建立模型上存在差异，多以多元逐步回归(SMLR)和偏最小二乘回归(PLSR)等统计方法为主。如Conforti等[14]采集了215个不同土壤类型和侵蚀条件的土壤样品，建立了土壤有机质PLSR估算模型，结果显示该模型的判断系数(R2)为0.84，RPD为2.53；王超等[15]利用SMLR方法构建了不同光谱处理方式的褐土有机质光谱，基于一阶微分预处理构建的模型R2都在0.92以上；刘磊等[16]采用SMLR和PLSR方法建立了江西省红壤的有机质含量估算模型，R2分别为0.78、0.99。由于土壤反射光谱数据的复杂性，向量机回归(SVR)、随机森林(RF)、人工神经网络(ANN)和BP神经网络(Back propagation neural network)等非线性回归方法越来越多地被应用到土壤有机质含量估算的研究中。纪文君等[17]采用SVR和RF方法建立土壤有机质含量反演模型，R2分别为0.927和0.915；Daniel等[18]采用400～1 100 nm的可见光-近红外光谱结合人工神经网络(ANN)方法建立了土壤有机质的估算模型，决定系数(R2)达到0.86；叶勤等[19]利用BP神经网络法建立了陕西省横山县的土壤有机质含量估算模型，模型决定系数(R2)达到0.8930。与传统统计方法相比，机器算法能够较好地处理土壤有机质含量反演的非线性问题，建模效果较优，在估算土壤有机质含量方面具有较大的潜力。

多种多样的光谱变换方式及建模方法使得不同区域及不同学者所构建的土壤有机质估算模型难以通用。陕西省成土因素差异巨大，土壤类型众多，有机质差异明显，有利于从多土壤类型及宽土壤有机质含量的角度构建陕西省通用的土壤有机质估算模型。基于此，本文以陕西省9种主要土壤类型的土样室内光谱反射曲线与土壤有机质含量为数据基础，对光谱反射曲线进行多种变换，结合SLR、PLSR、SVR 3种建模方法构建不同的土壤有机质含量预测模型，对比分析其效果，筛选出最优的土壤有机质估算模型。

1 材料与方法

1.1 研究区概况

陕西省地处我国大陆腹地，处于105°29′～111°15′E和31°42′～39°35′ N，南北长约880 km，东西宽约160～490 km，土地总面积20.56万km2。全省纵跨黄河、长江两大流域，地形地貌复杂，总特点是南北高，中部低，海拔主要分布在500～2 000 m。境内气候差异显著，由北向南为温带、暖温带和北亚热带。年降水量由南向北递减，受山地地形影响比较显著，年平均降水量576.9 mm，年平均气温13.0℃，无霜期218 d左右，不同季节的水分干湿状况和气温状况差异显著。复杂的成土因素致使陕西省土壤类型众多，据全国第二次土壤普查全省共有22个土类，其中主要土壤类型包括塿土、水稻土、黄棕壤、黄褐土、黄绵土、黑垆土、风沙土、褐土及潮土等9种，土地利用方式包括旱地、林地、水田、园地、草地等。

1.2 土样采集与处理

根据陕西省土壤空间分布特征，2016年6—8月选取了51个具有代表性的土壤剖面，共计216个土壤样品，采样点分布如图1所示。野外挖掘标准土壤剖面(剖面深度120 cm以上)，记录成土因素信息，根据颜色、质地、结构等的差异划分发生学层次，每个剖面划分3～6层，观察形态特征，并逐层采集土样。包括塿土、水稻土、黄棕壤、黄褐土、黄绵土、黑垆土、风沙土、褐土及潮土等9种土壤类型(表1)。样品经风干除杂处理、过1 mm孔筛，采用四分法分为两份，一份用于室内土壤光谱反射率的测定，另一份运用重铬酸钾容量法—外加热法[20]来测定土壤有机质含量。

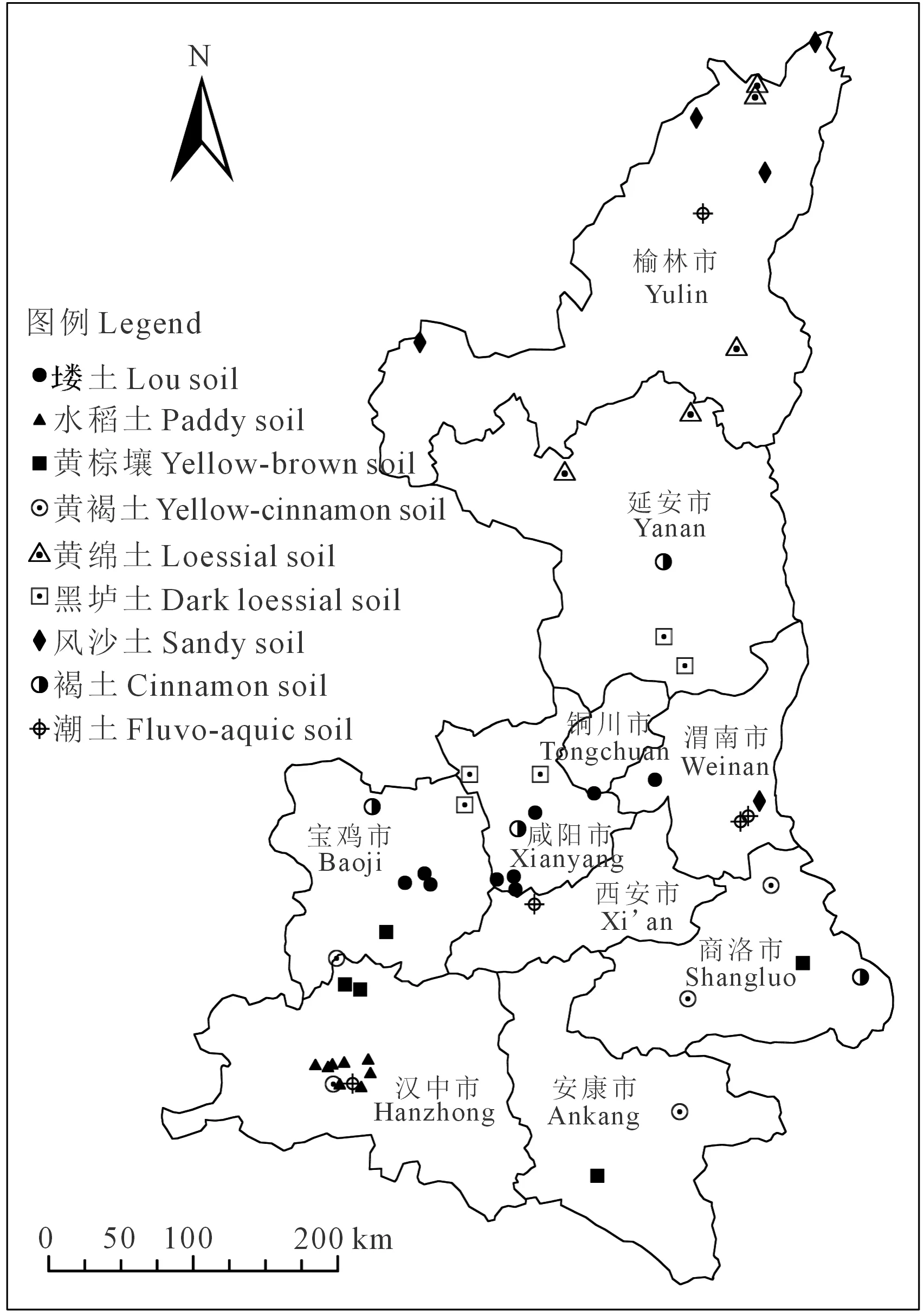
图1 采样点空间分布Fig.1 The spatial distribution of sampling locations

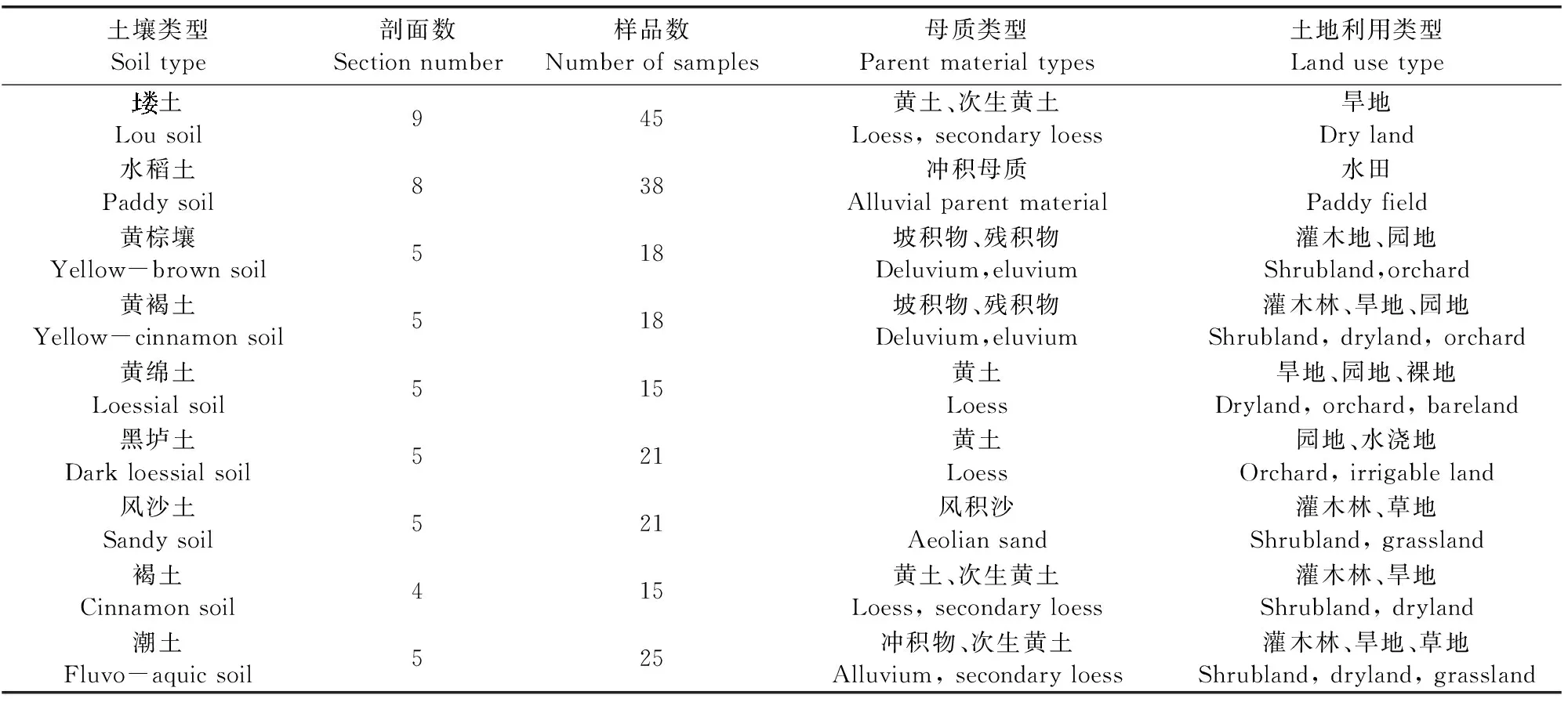
表1 土样基本信息

1.3 光谱测定与预处理

土壤光谱反射率采用美国Spectra Vista公司生产的SVC HR-1024 i便携式光谱仪测定，光谱采集范围为350～2 500 nm，光谱分辨率为≤3.5 nm(350～1 000 nm)、≤9.5 nm(1 000～1 850 nm)和≤6.5 nm(1 850～2 500 nm)。土样光谱采集工作在室内进行，将处理后的土样装进直径10 cm、深2 cm的玻璃器皿中，用直尺将土壤表面刮平，测定前需进行暗校正和白板校正，光源是功率为50 W的卤素灯，距离土壤表面30 cm，天顶角为15°，采用的探头视场角为8°，探头位于土壤表面垂直正上方15 cm处。每个土样测量4个方向，剔除异常波段的曲线，共采集12条光谱曲线，算术平均后作为该样品的光谱反射数据。

数据分析之前，每份土样去除噪声较大的350～399 nm和2 401～2 500 nm两个边缘波段，并采用小波包去噪法对光谱反射数据进行去噪处理[21]，得到重采样间隔为10 nm的原始光谱反射率曲线。光谱变换可以很大程度上消除土壤背景的影响，剔除无效光谱信息，进一步提高光谱信噪比，突出光谱的吸收和反射特征[22]。本文在建模之前，对原始光谱R进行一阶微分d(R)、倒数对数log(1/R)、倒数对数一阶微分d[log(1/R)]和去包络N(R)的变换，并采用Savitzky-Golay平滑(SG平滑)[23]及Norris平滑滤波[24]对原始光谱及其变换形式进行平滑处理，消除光谱噪音误差，提高模型估算精度，但应注意采用SG平滑时移动窗口宽度及多项式的优化选择。

1.4 敏感波段提取与特征参数构建

采用相关分析法来确定土壤有机质含量与光谱反射率及其变换形式的敏感波段，相关性越高，波段响应越敏感。将土壤有机质含量与原始光谱及其变换形式的光谱反射率进行相关性分析，并对相关系数在0.01水平上进行显著性检验，通过显著性检验的即为敏感波段[25-26]。利用400～2 400 nm波段的光谱反射率，系统构造原始光谱及其变换形式光谱两波段组合的差值指数DI(DI=Ri-Rj)、比值指数RI(RI=Ri/Rj)和归一化指数NDI(NDI=(Ri-Rj)/(Ri+Rj)，分析3类指数与土壤有机质含量之间的相关关系，筛选出最优的土壤有机质含量估算的光谱参数。相关分析和光谱参数计算分别在SPSS软件和Matlab 2018a中实现。

1.5 模型构建与精度验证

研究中反演模型的构建采用线性模型SLR和PLSR以及非线性数据挖掘技术SVR 3种方法。SLR法是以土壤有机质含量为因变量，土壤光谱反射率及其变换形式与有机质含量的相关系数属于0.01水平上显著相关且绝对值最大的波段作为自变量，建立一元线性回归模型[27]；PLSR方法能够消除波长变量共线性，解决因土壤各组分的吸收波段相互重叠干扰土壤有机质含量估算精度的问题，避免模型过度拟合[28]；SVR是支持向量机函数在回归领域的应用，通过事先确定的非线性映射将输入向量映射到一个高维特征空间(Hilbert空间)中，然后在此高维空间中再进行线性回归，从而取得在原空间非线性回归的效果[29]。PLSR方法的建模和验证是在Unscrambler 9.7中完成，SVR法的建模和验证是在R软件中完成。

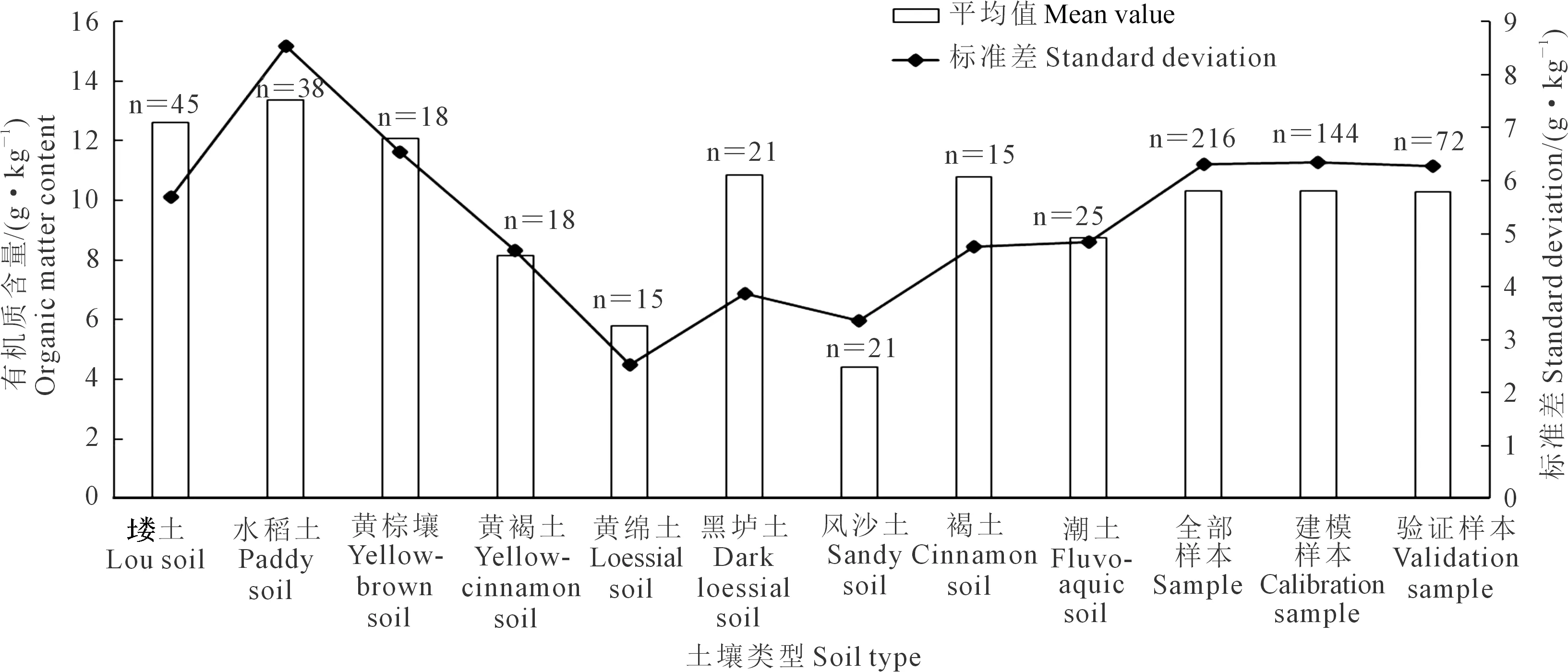
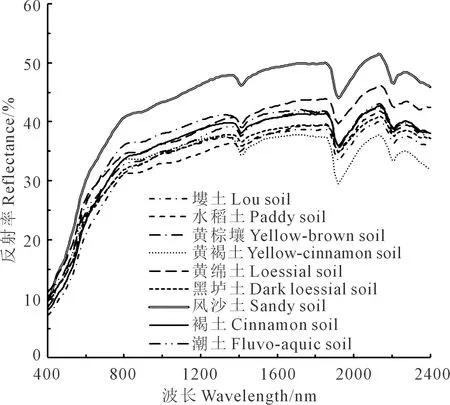
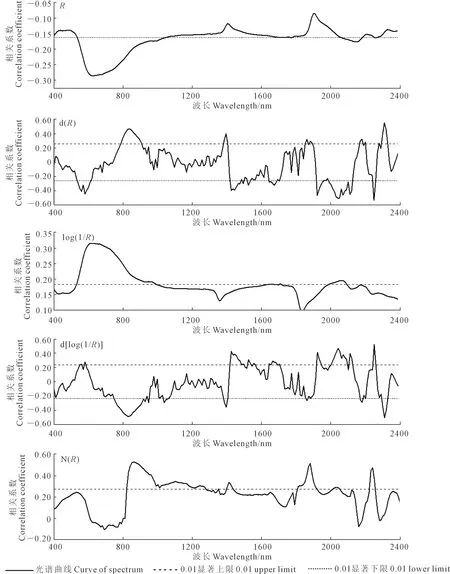
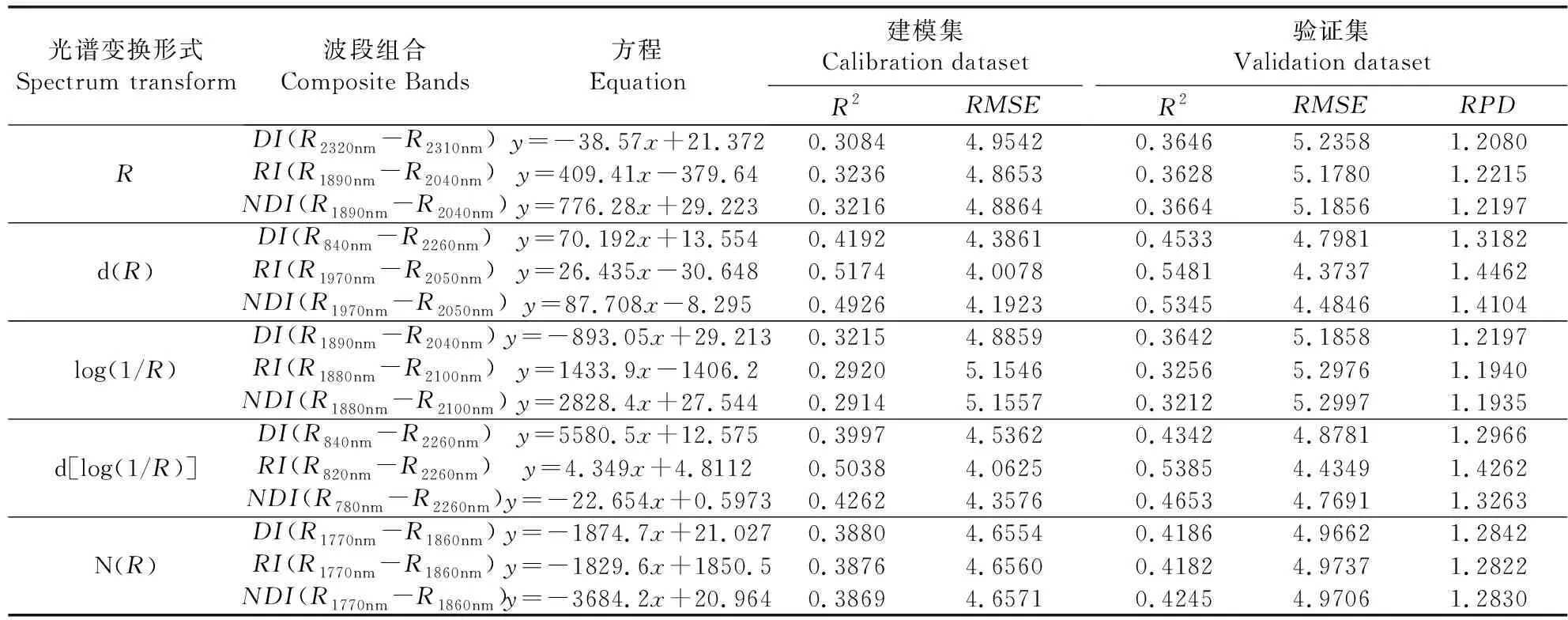
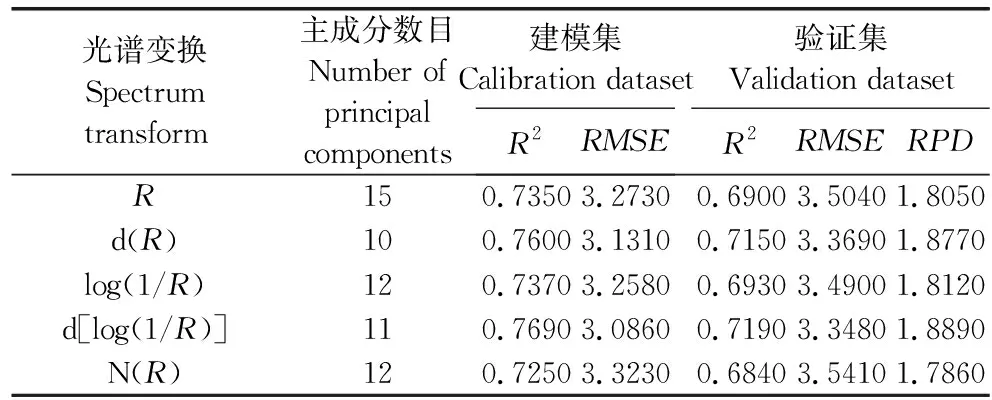
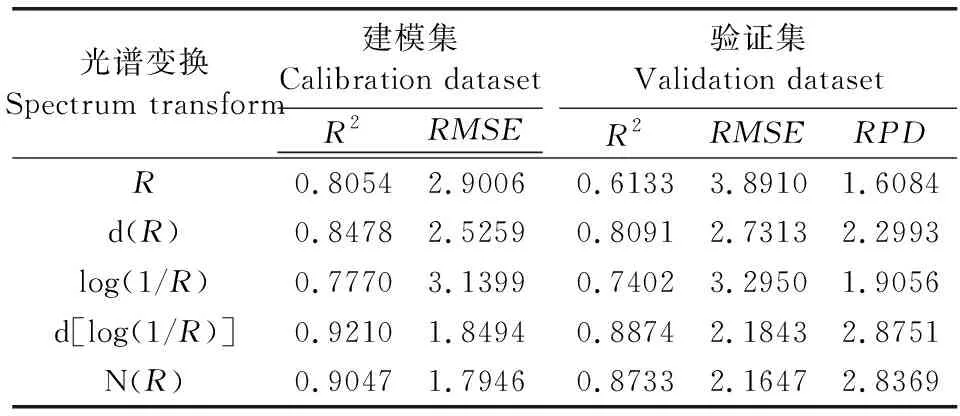
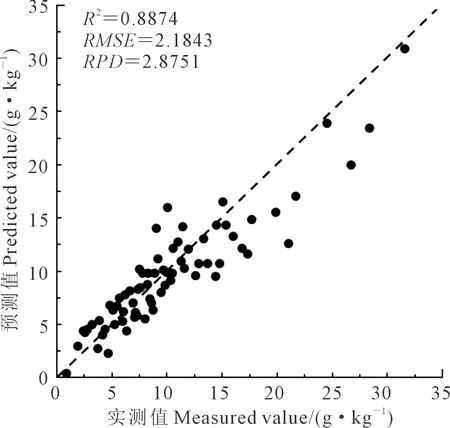
土壤有机质模型估算精度的验证采用决定系数(R2)，并结合均方根误差(RMSE)以及校正集的相对预测偏差(Relative percent deviation,RPD)等参数来进行模型对比评价[30]。建模集和验证集的交叉验证结果R2越大，RMSE越小，说明模型稳定性越强，估算精度越高。另外，RPD表示模型的预测能力，一般分为3类，当RPD≤1.4时，模型不可靠，无法对土样进行预测；当1.4

2 结果与分析

2.1 不同类型土壤有机质含量统计及光谱特征

将所有土壤样品按有机质含量从低到高的顺序，以2∶1的比例分为建模集和验证集，得到144个建模样本和72个验证样本，见图2。所采集的土壤样本中，有机质含量分布范围为0.66～35.43 g·kg-1，平均值为10.32 g·kg-1。建模样本和验证样本与总体样本的各统计量基本都在同一水平，标准差较小，说明样本数据的选取较为合理，代表性较强。

图2 不同类型土壤有机质含量的统计描述Fig.2 Statistical description of organic matter content in different soil types

图3为不同类型土壤的光谱反射曲线，可以看出，不同类型土壤光谱曲线形态基本相似，土壤光谱反射率随波长的增大而增大，在可见光波段范围反射率呈明显的上升趋势，而近红外波段反射率增加缓慢，且出现波折，在1 400、1 900 nm和2 200 nm等波段附近具有强烈的水分吸收谷，常认为与OH、H2O、Al-OH和Mg-OH谱带有关[11,32]。结合表1，水稻土与塿土的有机质含量较高，光谱反射曲线处于较低位置；风沙土的有机质含量均值最小，光谱反射率最高；黄褐土的光谱曲线在1 400 nm以后表现出较低的反射率，这可能与黄褐土的土壤含水量相关。

图3 不同类型土壤的高光谱反射特征Fig.3 Hyperspectral reflection characteristicsof different soil types

2.2 土壤有机质含量与土壤光谱的相关性分析

图4为土壤有机质含量与R、d(R)、log(1/R)、d[log(1/R)]和N(R)之间的相关性分析结果。可以看出，在全波段范围内，R与有机质含量呈负相关，在540～1 050 nm附近有较强烈的低谷；而log(1/R)与有机质含量呈正相关，与R的相关性变化规律正好相反；d(R)、d[log(1/R)]和N(R)的相关系数呈现较强的正负交替变化，与R的相关性变化相比均有所增强，这说明经过变换处理的光谱可以进一步增强光谱数据与土壤有机质含量之间的反射率，提高模型估算精度。其中微分变换能够较好地消除噪音、背景等影响，进一步挖掘土壤隐含信息，提高土壤有机质含量与光谱的相关性。

图4 土壤有机质与原始及变换光谱反射率的相关系数Fig.4 Correlation coefficient between soil organic matter and the original and transformed spectral reflectance

不同地区不同类型土壤的有机质高光谱响应波段并不一致，将土壤有机质含量与5种不同形式光谱反射率进行相关性分析，并对相关系数在0.01水平上进行显著性检验，共有R的540～1 050 nm、1 720～1 740 nm、1 780 nm、2 080～2 190 nm、2 270～2 280 nm，d(R)的540～610 nm、790～910 nm、1 390～1 540 nm、1 650～1 710 nm、1 860～2 130 nm、2 180～2 210 nm、2 260～2 330 nm，log(1/R)的540～1 030 nm、1 700～1 790 nm、2 080～2 180 nm，d[log(1/R)]的550～580 nm、750～950 nm、1 040～1 060 nm、1 390～1 570 nm、1 650～1 710 nm、1 870 nm、1 930～1 950 nm、2 010～2 130 nm、2 180～2 190 nm、2 310～2 330 nm，N(R)的820～1 270 nm、1 350 nm、1 400～1 430 nm、1 810～1 910 nm、2 010～2 050 nm、2 230～2 250 nm等70个波段通过检验，可以应用于土壤有机质含量高光谱模型的估算。

2.3 土壤有机质含量的一元线性回归(SLR)估算模型

在构建SLR反演模型时，单波段的光谱反射率容易受外部环境的影响，难以精确估算土壤有机质含量。解宪丽等[33]提出利用波段组合方法构建的反演模型精度要优于单波段预测方法，且模型可靠性较强。本文运用R、d(R)、log(1/R)、d[log(1/R)]和N(R)两波段的DI、RI、NDI光谱指数，研究它们与土壤有机质含量之间的相关关系，并以光谱反射率两波段组合的3类指数得到的最高相关系数入选的波段为自变量，土样有机质含量实测值作为因变量，建立土壤有机质含量SLR模型，并对估算模型进行检验。由表2可知，SLR模型精度整体较差，最高决定系数仅为0.50左右，其中d(R)光谱和d[log(1/R)]光谱建立的模型效果优于其他形式光谱，以d(R)光谱的RI(R1970nm-R2050nm)结果最好，决定系数(R2)分别为0.5174和0.5481，RMSE分别为4.0078和4.3737，验证RPD仅为1.4462，只能对土壤有机质含量进行粗略估算，说明SLR方法并不适用于陕西省土壤有机质含量估算模型的建立。

表2 基于光谱特征指数的土壤有机质SLR模型检验结果

2.4 基于偏最小二乘回归(PLSR)的土壤有机质估算模型

将土样的有机质含量实测值作为因变量，通过相关分析入选的相关系数较高的70个波段为自变量，建立土壤有机质含量PLSR模型，建模过程对70个敏感波段进行主成分提取，结果见表3。可以看出，所有光谱数据建模决定系数均在0.72以上，与SLR模型相似，以d(R)和d[log(1/R)]光谱建模效果最优，说明对R进行微分变换后，可以增强光谱对土壤有机质的敏感性，提高模型精度。利用独立样本对5种光谱进行检验，验证集最优为d[log(1/R)]光谱反演的PLSR模型，R2、RMSE和RPD分别为0.7190、3.3480和1.8890。这一估算效果较SLR模型中d(R)光谱的RI(R1970 nm-R2050 nm)效果有所提高，但PLSR模型的RPD均未达到2.0，模型效果一般，只能对土壤有机质含量进行粗略估算。但采用PLSR方法建立的土壤有机质含量模型整体精度较SLR模型有了显著提高，原因可能是土壤有机质组成复杂，与光谱之间不是简单的线性关系，PLSR可以运用主成分提取到对土壤有机质含量相关性最大的波段范围，从而减少光谱维数。

表3 基于光谱特征参数的土壤有机质PLSR模型估算结果

2.5 基于支持向量机回归(SVR)的土壤有机质估算模型

支持向量机回归法是一种较好地实现了结构风险最小化思想的方法，具有机器学习理论和技术，将神经网络的学习算法纳入了核技巧范畴[34-35]。利用SVR方法，基于土壤光谱反射率及其4种变换处理，建立土壤有机质含量SVR模型。由表4可以看出，d(R)、d[log(1/R)]和N(R)验证集R2均达到了0.80以上，RMSE均小于3.00，RPD均在2.20以上，具有较好的估算土壤有机质含量的能力。与PLSR模型相同，d[log(1/R)]建模表现效果最好，建模集和验证集R2最高，分别为0.9210和0.8874，RMSE分别为1.8494和2.1843，RPD达到2.8751。图5为使用d[log(1/R)]光谱建立的SVR模型的检验结果，通过有机质含量实测值与预测值的对比可以看出，建模样本和验证样本都趋于1∶1直线附近，估算精度较高。结合表3，基于d[log(1/R)]光谱基础上，SVR模型的建模和验证R2分别比PLSR高了0.152和0.1684，RMSE分别低了1.2366和1.1637，估算精度明显优于PLSR模型。因此，d[log(1/R)]光谱建立的SVR模型是3种建模方法中的最优估算模型。

表4 基于光谱特征参数的土壤有机质SVR模型估算结果

图5 d[log(1/R)]光谱建立的SVR模型的检验结果Fig.5 Test results of SVR model establishedby d[log(1/R)] spectrum

3 讨 论

土壤有机质是动植物残体在微生物矿化作用下形成的有机物质的总称，因其主要组成部分腐殖质呈现黑色而表现出吸收光谱的特征，且有机质在土壤中的质量分数较大，吸收特征明显。通过对土壤有机质含量与土壤光谱之间的相关性分析，发现土壤有机质含量与土壤光谱在400～2 400 nm整个波段范围内呈负相关关系，这与前人研究结果基本一致[36]。土壤有机质含量与原始光谱的相关性较低，且光谱数据的采集容易受土壤本身及外界环境的影响，因此，对原始光谱R进行不同形式的变换处理可以有效提高反演模型的精度。通过4种形式的光谱变换处理，发现d(R)、d[log(1/R)]和N(R)变换后光谱反射率与土壤有机质含量间的相关性有了显著提高，相关系数最高分别达到了0.556、0.523和0.527，说明进行微分变换能够有效地突出光谱之间的差异特征、滤掉光谱近线性背景噪声干扰，进而提高土壤有机质含量的预测精度[37]；N(R)变换后可以有效地突出光谱曲线的反射和吸收特征，并将其归一化到一致(0～1)的背景上，有利于不同光谱曲线之间进行特征数值的比较分析[38]，两种变换方式对于提高估算模型精度发挥了重要作用。经过log(1/R)变换后的建模效果不及d(R)和d[log(1/R)]光谱，说明log(1/R)变换不适用于陕西省土壤有机质含量的估算建模。

本研究综合对比SLR、PLSR和SVR 3种建模方法在陕西省土壤有机质含量高光谱反演模型的应用，发现3种方法的建模效果是不相同的。利用SLR方法建模反演时，系统构造了400～2 400 nm光谱的两波段的DI、RI和NDI指数与土壤有机质含量的关系，发现d(R)光谱的RI(R1970 nm-R2050 nm)结果最好，RPD最高为1.4462，只能够对有机质进行粗略估算。基于R、d(R)、log(1/R)、d[log(1/R)]和N(R)5种光谱在显著性波段基础上的建模结果，SVR模型的建模R2比PLSR模型分别增加了0.0704、0.0878、0.0400、0.1520和0.1797，RMSE分别减小了0.1420、0.6051、0.1181、1.2366和1.5284，RPD除R外分别增加了0.4223、0.0936、0.9861和1.0509，说明SVR法的建模精度要高于PLSR法，且能对土壤有机质进行较好估算，这与前人研究结果基本一致[17]。3种方法比较而言，SLR法处理非线性的能力较差，极易产生随机性[28]；PLSR法可以满足土壤有机质含量光谱反演的基本需要，建立的模型比较简单；SVR法能够在高维空间里处理非线性问题，具有强大的泛化能力，但需要对原始光谱进行不同形式的变换。d [log(1/R)]光谱建立的SVR模型是本文效果最优的土壤有机质含量估算模型，建模和验证R2分别为0.9210和0.8874，RMSE分别为1.8494和2.1843，RPD为2.8751，基于此模型反演土壤有机质含量具有较高的精度，可以有效、精准地监测陕西省土壤有机质含量，是估算陕西省土壤有机质的最优反演模型，适用性较强，在未来的研究中可以得到更加广泛运用。

4 结 论

本文基于陕西省9种不同类型土壤样品的室内高光谱和土壤有机质数据，基于4种光谱变换和SLR、PLSR、SVR 3种建模方法建立了陕西省土壤有机质含量高光谱反演模型，比较了不同光谱数据变换处理和不同建模方法下建模集和验证集估算模型精度的差异。d[log(1/R)]和d(R)变换明显提高了土壤有机质含量与光谱反射率的相关性，SVR模型估算土壤有机质含量的精度较SLR模型和PLSR模型有显著提高，通过敏感波段建立的SVRd[log(1/R)]回归模型是估算土壤有机质含量的最优模型。