矫直单元段带材打滑分析

胡 林

(中色科技股份有限公司， 河南 洛阳 471039)

拉弯矫直机的工作原理为通过拉伸和弯曲作用对带材产生塑性延伸，从而矫正带材板形。铝板带的生产中，为保证其板面质量需避免带材与工作辊间出现打滑现象。在设计中，通常需要计算矫直单元的工作辊与带材间的摩擦力以验算工作辊塔形角及带材包角的适用性。在生产实践中，需要了解带材与工作辊之间是否出现了打滑，为矫直单元的张力设置，带材速度控制精度评价提供指导。因此，我们需要了解在矫直段影响带材最大加速度的相关因素，以避免带材出现打滑现象。

整个诵读活动分为三个篇章：从中国共产党成立到新中国成立——经典的深度·革命的力度；从新中国成立到十一届三中全会——经典的温度·建设的热度；从十一届三中全会召开至今——经典的亮度·改革的向度。16个单位的党员教师用朗诵、合唱、舞蹈等形式讴歌伟大的中国共产党。

当带材加速度超过在摩擦力作用下工作辊所能达到的最大加速度时，带材将出现打滑现象。带材经过工作辊时形成包角，但由于存在弹塑性弯曲力矩的原因，此包角与工作辊几何切线形成的包角并不重合。为方便力学分析,本文研究的带材为屈服强度较低且较薄的铝合金。在这种情况下，工作辊几何切线形成的包角与带材经过工作辊形成的包角较为接近，在计算中可以做近似相等处理。

1 工作辊受力分析

带材在经过矫直单元时，一般要受到三组下辊组及两组上辊组的弯曲矫直作用(图1)。图(2)为上工作辊的受力分析图，为保证上辊系工作辊、中间辊及支承辊间的紧贴关系，对带材有最小张应力要求。

2.5 两组手术前后CSI及BSI比较 术前，两组CSI及BSI比较，差异无统计学意义(P>0.05)；术后，两组CSI及BSI均下降，组间比较差异无统计学意义(P>0.05)。见表5。

图1 带材经过矫直辊组示意图Fig.1 Schematic diagram of strip passing through straightening roller set

图2 工作辊受力分析Fig.2 Working roll force analysis

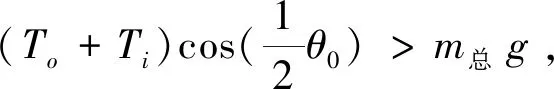
带材经过工作辊时形成包角θ0，其与工作辊间的摩擦系数为f。矫直单元工作时，需向带材表面喷射清洗油，因而摩擦系数f应按铝与钢摩擦副在有润滑状态下的工况选取。喷油时，上、下辊系工作辊与带材之间形成油膜，但由于重力原因，带材下表面的油膜质量不如上表面的理想，结合生产实践，上、下辊系工作辊与带材间的摩擦系数分别取0.02和0.025。由物理学欧拉公式可得工作辊入口侧带材张力Ti与出口侧带材张力To的关系，To=Tieθ0f；式中，工作辊入口侧带材张力Ti=λσsbh，带材张应力系数λ=σ0/σs，σ0为工作辊入口侧带材张应力，σs为带材屈服应力，b为带材宽度，h为带材厚度。

式中，fzc为支承辊轴承摩擦因数，取0.002；rzc为支承辊轴承滚子滚动半径。由于辊系呈塔形布置，因而由估算公式计算得出的M2值偏小。第三部分则是辊系密封圈的转动阻力矩M3的影响，此部分阻力矩在新辊系时数值较大，辊系运行一段时间后会有所下降，且不同矫直机组的辊系其值也不同，结合支承辊的启动力矩及生产经验，本文在公式代入数值计算时，其值取为1000Nmm，M3=1000Nmm。第四部分则是由于支承辊及中间辊在加速时使中间辊对工作辊的静摩擦力增加而产生的额外阻力矩M4。

工作辊的转矩公式，M0-(M1+M2+M3+M4)=Jgεg；式中，Jg为工作辊转动惯量；εg为工作辊角加速度。根据角加速度与加速度关系，可以得出带材加速度ad计算公式，ad=εgrg。

高层建筑二次供水设备（变频水泵加水箱）选型及施工……………………………………………………… 许毅彬（7-20）

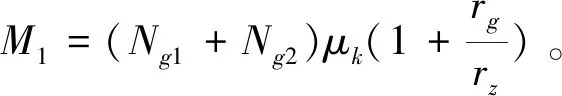
2 工作辊打滑分析

中间辊对工作辊的静摩擦力大小受多种因素的影响，本文对与之有关的参数取值时只做估算处理。为方便计算，相关参数取值如下：Fx=M3/rg，Fy=0，M4=∑Jiεi，Ji为各中间辊及支承辊的转动惯量，εi为各中间辊及支承辊角加速度。为方便分析，其它参数将按照某项目1450mm矫直单元设计参数代入，某项目1450mm矫直单元相关参数取值如下：b=1450mm，h=0.2mm，σs=100MPa，rg=15mm，mg=9.21kg，θ1=84°，μk=0.5mm，rz=20mm，Jg=1036kg·mm2，m总=66kg，rzc=14.5mm。

在分析应力系数λ对带材加速度ad的影响时，本文选取工作包角θ0=165°，得出λ>0.083。取λ值从0.1递增至0.5，可计算得出带材加速度ad，将计算结果绘制成曲线(图3)。分析可知，带材加速度ad与应力系数λ近似呈线性关系，ad随着λ的增加而增大，所以为避免打滑，可以通过增大带材应力系数λ的方式；且在相同情况下带材加速度ad下辊系的要大于上辊系的，即上辊系更容易打滑。

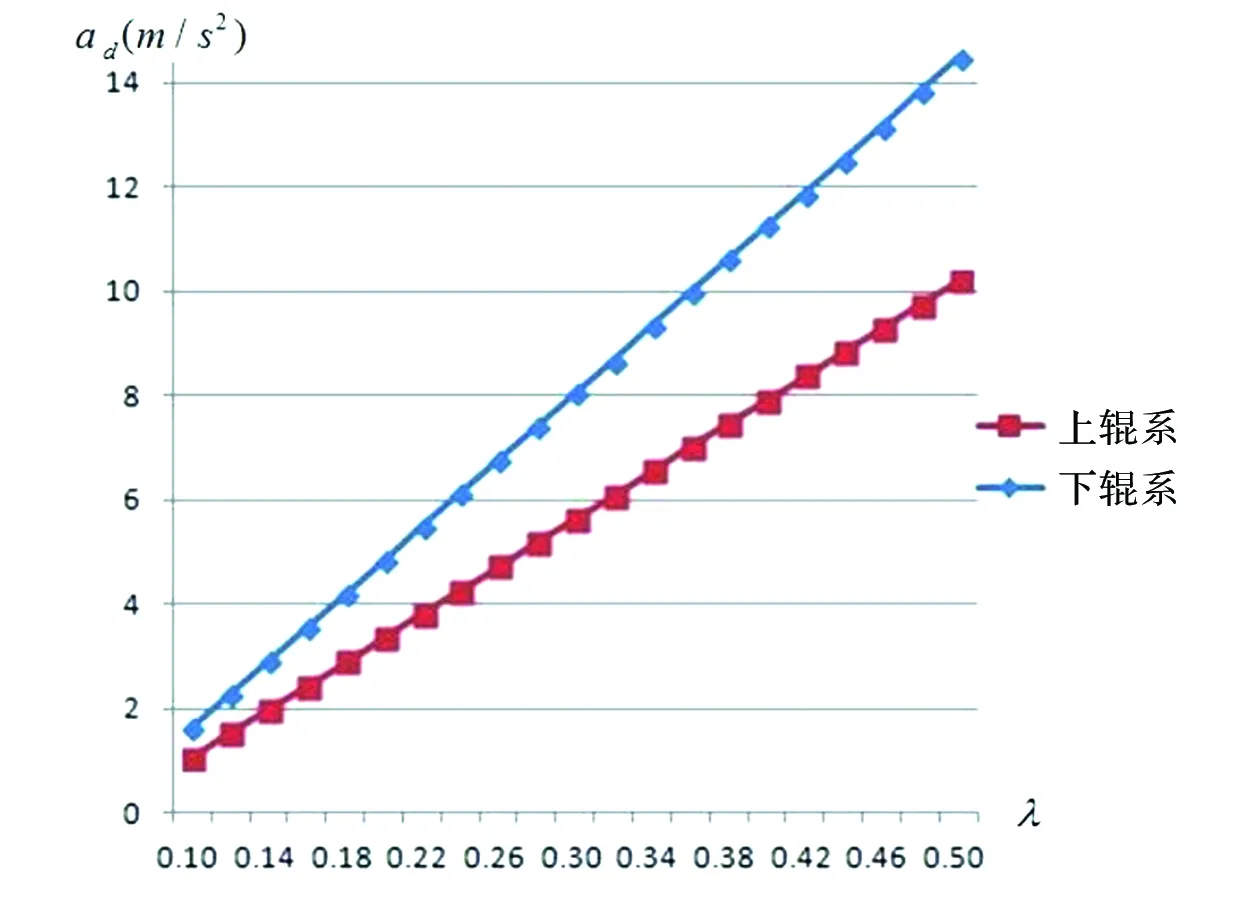
图3 应力系数对带材加速度的影响Fig.3 Effect of stress coefficient on acceleration of strip

工作包角θ0=160°时，计算可得λ>0.062；工作包角θ0=175°时，计算可得λ>0.248。于是在分析工作包角θ0对带材加速度ad的影响时，选取λ=0.3。取θ0值从160°递增至175°，计算得出带材加速度ad，将计算结果绘制成曲线(图4)。

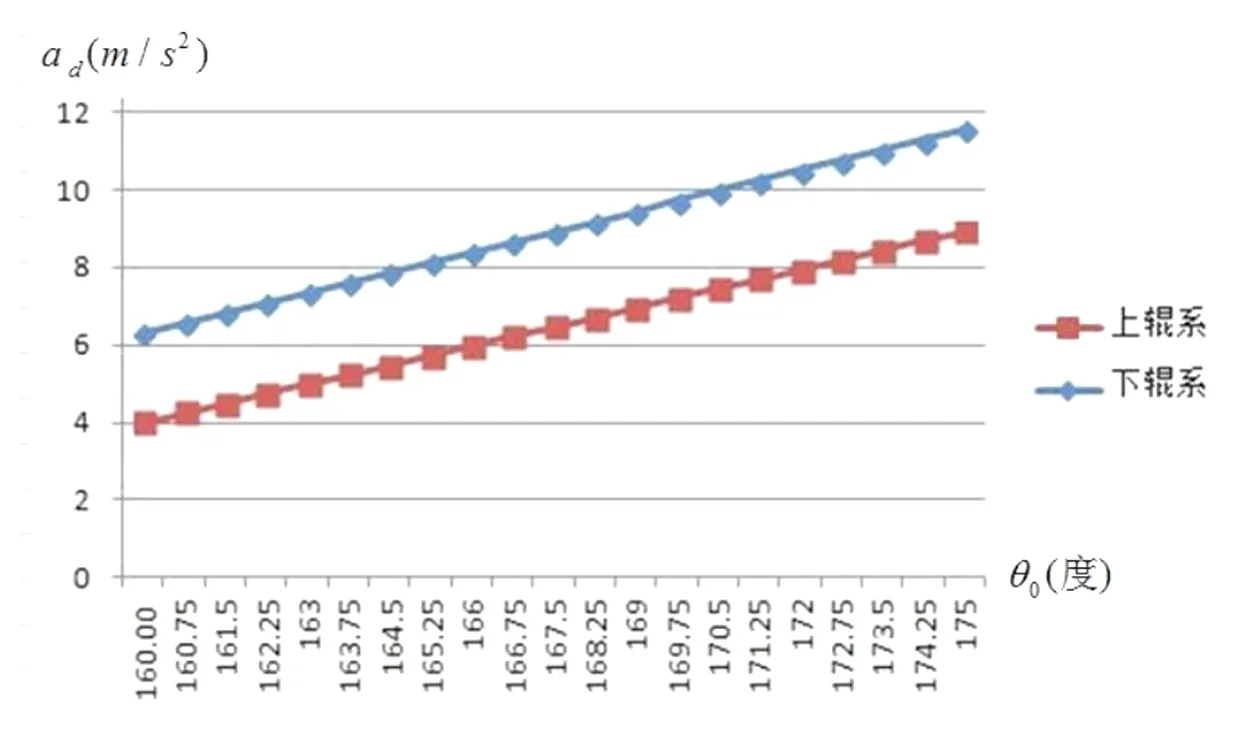
图4 工作包角θ0对带材加速度ad的影响Fig.4 Effect of working angle on strip acceleration

分析可知，带材加速度ad与工作包角θ0近似呈线性关系，ad随着θ0的增加而增大，所以为避免打滑，也可以通过增大带材工作包角θ0的方式；且在相同情况下带材加速度ad下辊系的要大于上辊系的，即上辊系更容易打滑。

进了门，在没有见到任何人之前，我就认定是在这里了。是空气告诉我们的。空气中弥漫着奇异的香气，让人有微微的麻醉和眩晕之感，但心的悸动就在这种奇特的香氛当中，平静到迟慢。

3 结语

通过对矫直单元段带材最大加速度ad的公式推导，明确了应力系数λ、带材工作包角θ0与带材最大加速度ad的关系。并通过绘制曲线图的方式可知，为避免带材与工作辊间的打滑，可通过增大带材应力系数λ(即增大带材在矫直段的张力)或者工作包角θ0的方式；同时可知，带材在上辊系工作辊处比下辊系工作辊处更容易打滑。