Thermo-bioconvection transport of nanofluid over an inclined stretching cylinder with Cattaneo–Christov doublediffusion
2021-08-10HassanWaqasUmairManzoorTaseerMuhammadandSajjadHussain
Hassan Waqas,Umair Manzoor,Taseer Muhammad and Sajjad Hussain
1 Department of Mathematics,Government College University Faisalabad,Layyah Campus 31200,Pakistan
2 Department of Mathematics,College of Sciences,King Khalid University,Abha 61413,Saudi Arabia
3 Mathematical Modelling and Applied Computation Research Group(MMAC),Department of Mathematics,King Abdulaziz University,PO Box 80203,Jeddah 21589,Saudi Arabia
Abstract In this paper,Newtonian nanofluid flow is observed under the effects of the magnetic field,activation energy and motile microorganisms over an inclined stretchable cylinder.The magnificent aspects of nanoliquid are demonstrated by enduring the Brownian motion and thermophoresis diffusion features.Nonlinear higher order partial differential equations are transformed into first-order ordinary differential equations with suitable similarity variables.The attained sets of governing equations are then cracked by bvp4c procedure in MATLAB mathematical software.The numerical and graphical outcomes of controlling parameters such as Prandtl number,mixed convection,activation energy,thermophoresis,Brownian parameter,Biot number,Lewis number,Peclet number and motile concentration parameter against the velocity,temperature,volumetric concentration and motile concentration of nanoparticles of the fluid are discussed.The velocity is enhanced with the growth valuation in mixed convection and decay by rising variation of buoyancy ratio parameter,magnetic parameter and bio-convective Rayleigh parameter.The evolution in motile microorganisms is due to the increasing values of microorganisms Biot number.The presented data can be helpful in enhancement of manufacturing processes,biomolecules,extrusion systems applications and energy production improvement.
Keywords:bio-convection,magnetic-nanofluid,Cattaneo–Christov theory,motile microorganisms,inclined stretching cylinder
Nomenclature



1.Introduction
In recent years,scientists have shown remarkable interest to study the heat transport of nanofluid through a stretchable cylinder due to its implications in a wide variety of engineering and industrial applications.Concerning the physical and chemical characteristics of nanofluids,in addition to their superior thermal efficiency,nanofluids can be effectively used in a wide range of potential applications,such as heat exchangers,radiators,domestic refrigerator-freezers,glass blowers,electronic cooling systems(such as flat plates),crystal-growing,solar water heaters and paper products.Nanofluids are suspended nanoparticles with a diameter of<100 nm considered for enhanced heat conductivity.There are many uses of nanofluids in cooling devices,nuclear reactors,micro-electronics and transformer oils.
The main idea of nanofluid is given by Choi[1].He anticipated that the involvement of metal nanoparticles in the base fluid would improve the thermal conductivity of the regular specific fluid and stimulates the growth of these liquids for heat transfer.Nanofluids have claims for sun powered water warming,upgraded transport,heat move of fridges and coolers,and ideal assimilation of sunlight-based energy.Irfan et al[2]explored the impact of activation energy on Carreau nanofluids because of the contracting/extending layer within the sight of convective conditions,Joule heating and heat source/sink.An investigation to fabricate and comprehend numerical demonstrating for non-Newtonian Williamson liquid for portraying the warm qualities of nanofluid is given by Hashim et al[3].The objective of Moradi et al[4]was to do an exploratory investigation of the warmth move properties of multi-walled carbon nanotube nanofluids by the utilization of permeable media by a twofold line heat exchanger.Early examinations have made up for the unique consideration paid to improving energy development by working with nanoparticles to determine this perilous issue.On the slip side,within the sight of non-Newtonian nanofluids,the impacts of liquid stream,the warmth move of nanoparticles and the gyrotactic microorganism are discussed by Khan et al[5].They found that nanofluid stream,heat move,and gyrotactic convergences of microorganisms had utilitarian ramifications for inactively directed nanofluid limit model comparative with effectively controlled nanofluid conditions.Zuhra et al[6]explored the gyrotactic microorganisms and nanoparticles alongside viscoelastic nanofluid and heat move at higher temperatures with the thermophoresis boundary.The latest EMHD nanofluids motion computational technology model on a fixed thickness sheet with fixed fluid characteristics is explored by Irfan et al[7].The motion of chemically reacting stagnation point Powell–Eyring nanofluids by inclination cylinder with Cattaneo–Christov heat transfer is explored by Reddy et al[8].The nature of nonlinear heat radiation via the movement of modified 2nd-grade nanoliquid was observed by Khan et al[9].Alghamdi[10]deliberated magnetized nanoliquid flow by rotatable disk.Action of nanomaterial to diffuse blood by cylindrical tube exploiting a single kernel is explored by Uddin et al[11].The non-uniform hemodynamic nanoliquid motion in the absence of an existing magnetic field is analyzed by Abbas et al[12].Several scientists’works on nanofluid are supported via attempts[13–23].

Figure 1.Flow field and coordinate system.
The transient heat/mass transfer properties during static film flash of aqueous NaCl solution though experiments with water film concentration is investigated by Zhang et al[24].A comprehensive numerical study of heat transfer model including both conduction and radiation under contact and non-contact conditions was anticipated by Wang et al[25].Jia et al[26]examined the thermally conductive polymer composites with the integration of superior thermal conductivity.
Bioconvection can be categorized as the spectacle of the macroscopic motion of the fluid created by the gradient of density that has been formed by the collective directional swimming of micro-organisms.Such micro-organisms can be categorized as gyrotactic,oxytactic,gravitaxis and chemotaxis depending on the cause of implementation.Such selfpropelled micro-organisms want to collect near upper zone of liquid layer so that they pass there,which builds up a thick upper surface and become unstable/destabilized.Then upward swimming induces microorganisms to crumble and macroscopic convection to form.Bioconvection can be used in a wide variety of applications such as biological applications and microsystems,the pharmaceutical industry,biopolymer synthesis,environmentally safe applications,sustainable fuel cell technologies,microbial enhanced oil recovery,biosensors and biotechnology,and continuous modifications in mathematical modeling.Improvements in laboratory and field testing are utilized to develop the design of such structures.Kuznetsov[27]developed the principle of nanofluid bioconvection.Bioconvection is an idea used to clarify the system of incautious model improvement in microorganism liquids,for example,microbes and green growth was explained by Ghorai and Hill[28].The homogenous miniature polar bioconvective liquid stream with nanoparticles and gyrotactic microorganisms is investigated by Atif et al[29].Two-dimensional bioconvection blended pressure liquid stream with nanoparticles and gyrotactic motile microorganisms is concentrated by Khan et al[30].A bioconvection stream of summed up 2nd grade nanofluid is explored by Li et al[31].The non-warm radiation impacts of the Oldroyd-B nanofluid stream by swimming motile microorganisms past the turning plate have inspected by Waqas et al[32].Number of researchers in bioconvection has been approved out by investigations[33–42].
Above works investigation stimulates the current study,the foremost impartial to examine the upshot of motile microorganisms,activation energy and Cattaneo Christov double-diffusion on the flow of Newtonian nanofluid over an inclined stretching cylinder.The leading expressions of energy,momentum,volumetric and motile concentrations are initially concentrated to a self-similar arrangement by using appropriate similarities.Then obtained system is cracked numerically by bvp4c scheme,a program in the MATLAB.The graphical results of prominent parameters against allcontrolling concentrations are illustrated through plots.
2.Mathematical modeling
Consider the flow of Newtonian nanofluid flow with the consequences of activation energy,magnetic field and motile microorganisms’concentration through the inclined stretching cylinder(see figure 1).Bioconvection mechanism and Buongiorno relation are delighted to illustrate Brownian and thermophoresis diffusions and motility of liquid because of motile microorganisms and nanomaterials.The relation for the Newtonian fluid is

in which equation(1)is a mathematical form of Newton’s law of viscosity.Hereτyxis shear stress andμis called dynamic viscosity.The power-law model is expressed in equation(2)which can be reduced to the Newton’s law of viscosity by puttingμ=kandn=1 where n is flow behavior index.Therefore

Equation(3)is kinematic viscosity.Flow concerning differential equations is given as:

with boundary conditions

In equations(1)–(10),the components of velocity across x and r axis are symbolized asuandvrespectively,ρffluid density,ρmdensity of microorganisms,ρfdensity of base liquid,μdynamic viscosity,kinematic viscosity,Cconcentration of nanoparticles,Ttemperature,Twand∞Ttemperatures at the surface and away from the wall respectively,DB,DTandDmBrownian diffusion,thermophoresis features and microorganisms diffusion coefficient respectively,Cwnanomaterial concentration due to stretching cylinder,∞Cconcentration of nanofluid away from the wall.Using the following similarity transformation to reduce the PDEs into ODEs:

where



The skin friction is specified as:
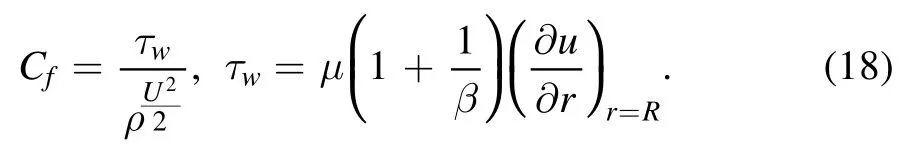
Equation(18)in dimensionless form is
The aspects for the local Nusselt,Sherwood and motile microorganism numbers are

These expressions are pre-arranged for the dimensionless form as
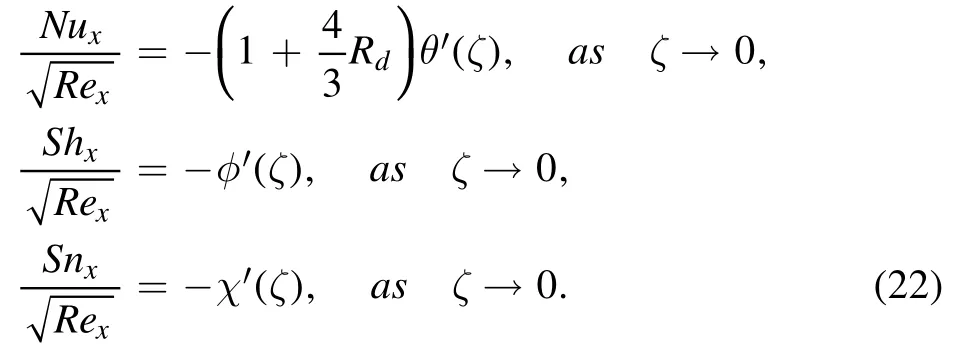
3.Numerical scheme
In this segment,the mathematical simulation of the flow model,equations(13)–(16)and boundary conditions(17)are transformed from PDEs to ordinary differential equations.For obtained numerical results,the bvp4c tool in MATLAB computational software is used.The governing equations are renewed from higher to 1st order as given below:



Figure 2.Significance of M on f′.

Figure 3.Significance of Nr on f′.

4.Results and discussion

Figure 4.Significance ofγ on f′.

Figure 5.Significance of Nc on f′.
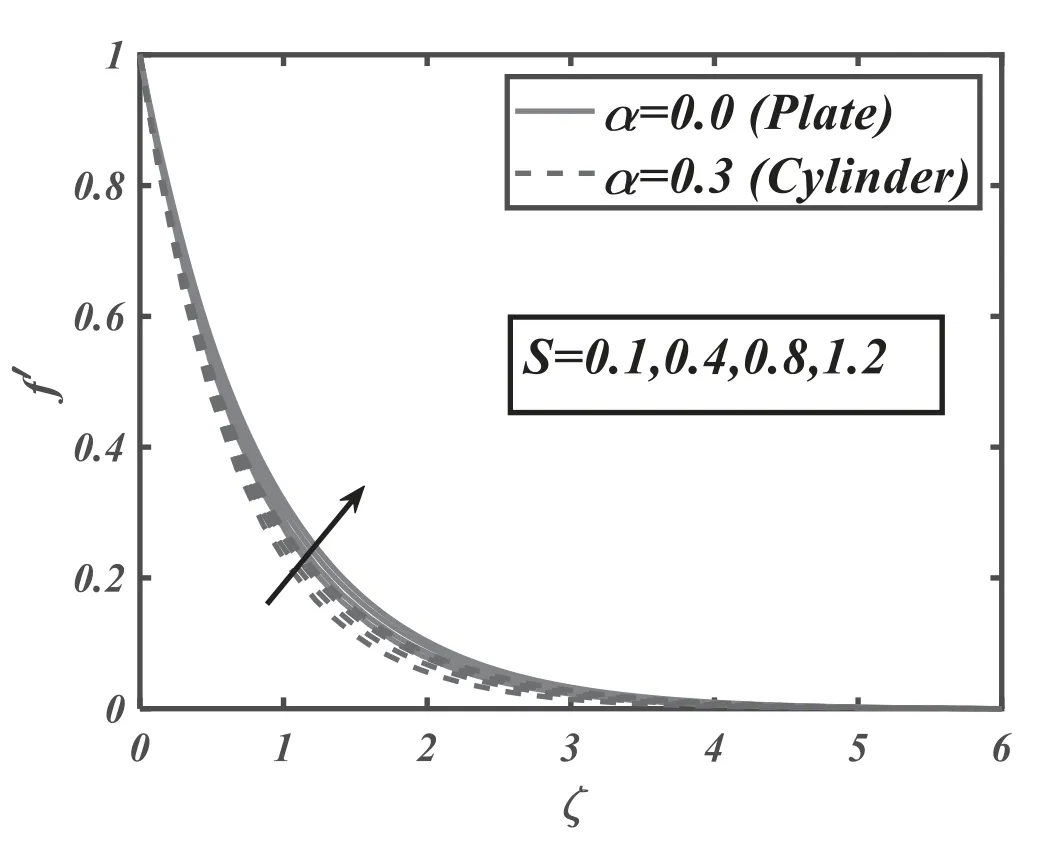
Figure 6.Significance ofS on f′.
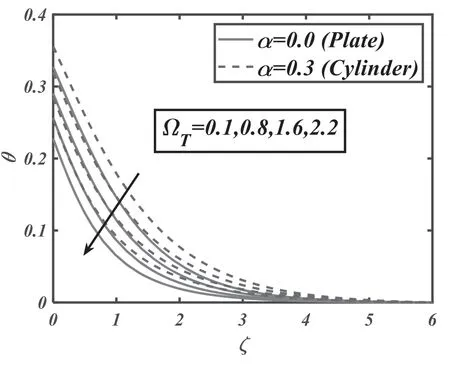
Figure 7.Significance of ΩT onθ.

Figure 8.Significance of Pr onθ.

Figure 9.Significance ofλ1 onθ.

Figure 10.Significance ofθw onθ.

Figure 11.Significance of Nb onφ.
The consequences of magnetic parameterMversus velocityf′are illuminated in the figure 2.Velocity of nanoliquidf′decays for growing data of magnetic parameter for both values(α=0 and 0.3).Significantly,this shows that growth in magnetic parameter values support the retarding force which promptly mark the fluid dynamic.The significance of the buoyancy ratio parameterNrfor the velocity profilef′is depicted in figure 3.Buoyancy-ratio number reduced thef′for both estimations(α=0 and 0.3).In figure 4,the effects of inclination for velocityf′are observed.The increasing inclination falls the velocity of the fluid for both cases(α=0 and 0.3).Figure 5 shows velocityf′for the various estimations of bio-convective Rayleigh parameterNc.Increasing behavior of bio-convective Rayleigh parameter declines velocity distribution for both situations(α=0 and 0.3).Figure 6 delineates the nature of the mixed convection parameter for velocityf′.The velocity of fluid magnifies for mixed convection parameter for both cases of plate and cylinder.Figure 7 reveals the effects of thermal relaxation parameter ΩTon the temperature fieldθ.From the curves,it is noted that the increasing thermal relaxation parameter reduces the temperature of the fluid.In figure 8,the nature ofPronθis explained.Temperature of liquidθdepreciated by Prandtl number for both values(α=0 and 0.3).This is due to the rising Prandtl number,which increases the heat transfer rate that cools the process and decreases the temperature within the boundary layer.Fluid with a progressive Prandtl number keeps low thermal conductivity,which diminishes the temperature and thermal boundary-layer thickness.Figure 9 elucidates the outcome ofλ1on temperatureθ.Temperature of the fluidθaugmented by swelling values of thermal stratification for both cases i.e.plate/cylinder.The impact ofθwagainst temperature profileθfor both cases(α=0 and 0.3)is explored in figure 10.It is regarded that the temperature of fluidf′boosted up by higher the variation of temperature ratio parameter.Figure 11 is reflecting the outcome ofNbfor the concentration fieldφ.It is logical that a rise in Brownian motion parameter decay the concentration of the nanoparticles for both values(α=0 and 0.3).In the nanofluid structure,because of the existence of nanoparticles,the Brownian motion occurs and with the intensification in Nb the Brownian motion is exaggerated and hence the nanoparticles concentration and boundary layer thickness reduce.Higher estimations of Brownian parameter fall boundary-layer thicknesses,as results the concentration reduces.To distinguish the consequences ofNtversus volumetric concentrationφ,figure 12 is portrayed.The thermophoresis parameter marks an increasing impact on the volumetric concentration of nanoparticlesφ.Nanoparticles wander from hot sector to cold sector owed to progressive thermophoresis evaluation.The nanofluid molecules kinetic energy is enhanced by swelling evaluation of thermophoresis parameter as a result of the concentration upsurges.Figure 13 is fixed to inspect the behavior of Prandtl numberPrfor concentrationφ.Rising estimations of Prandtl number decay concentration profile.Physically,the thermal boundary-layer drops with a higher variation of Prandtl and therefore,the concentration profile is dropped.Figure 14 elucidates the significance ofLeforφ.Concentration fieldφdecays for the great evaluation ofLefor both cases.Figure 15 lights the consequences ofEforφ.The concentration field is enhanced for increasing valuation ofEfor both values(α=0 and 0.3).Figure 16 demonstrates influence ofλ2onφfor both cases(α=0 and 0.3).Predictably,enhancing values ofλ2amplified concentration of nanoparticles.Figure 17 is captured to observe the concentration relaxation parameter effects Ωconφ.Growing relaxation parameter falls volumetric concentration profile of nanoparticles of the fluid.The upshot ofPeversus microorganismχis deliberated in figure 18.Microorganism fieldχis deteriorated for the advanced magnitude ofPe.Figure 19 explores nature ofLbversus microorganism fieldχ.Microorganismχdecays due to higher magnitude ofLbfor both cases(α=0 and 0.3).The upshot ofλ3forχis outlined in figure 20.The microorganism’s fieldχis boosted for higher variations of microorganism stratification Biot number.Table 1 illustrates that skin friction is boosted for magnetic parameter while it decreases for mixed convection parameter.Table 2 illustrates that Nusselt number is boosted for Prandtl number while decays for temperature ratio number.Table 3 illustrates that Sherwood number is upgraded for increasing values of Lewis number.Table 4 illustrates that density number of motile microorganism is boosted for bioconvection Lewis and Peclet numbers.
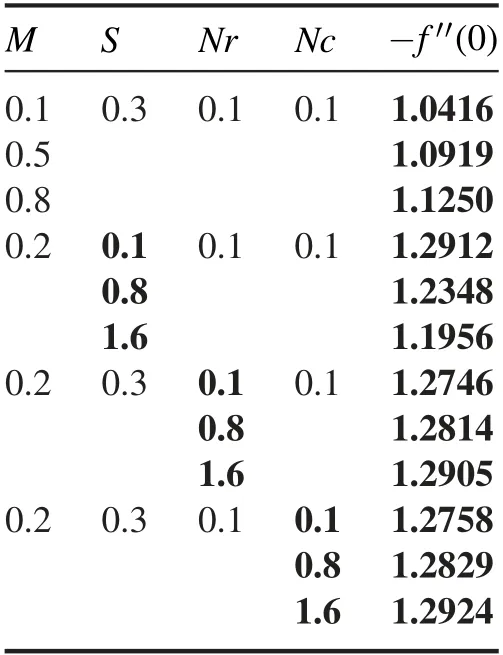
Table 1.Outcomes of-f′′(0)for varying M,S,Nrand Nc.
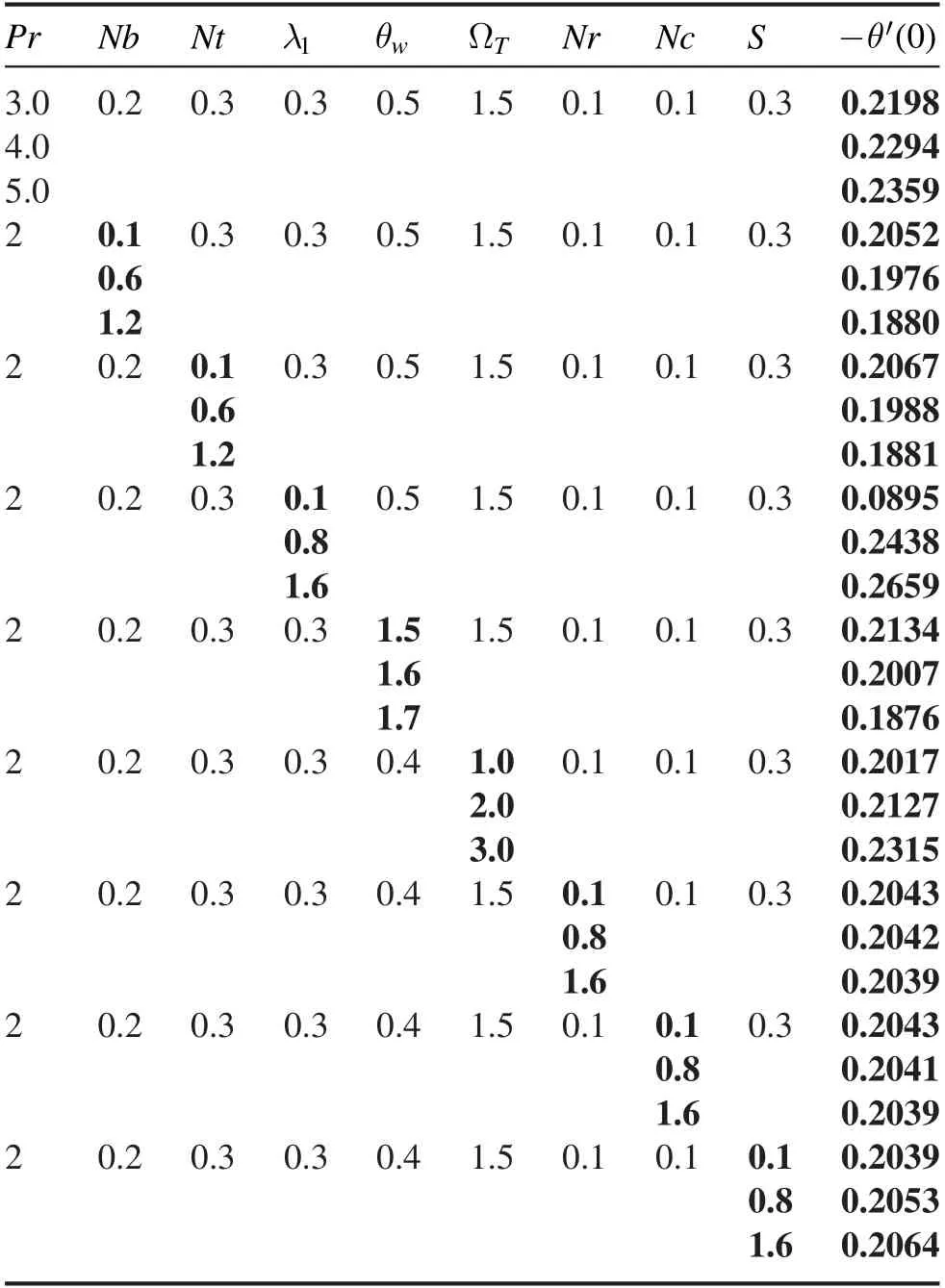
Table 2.Outcomes of-θ′(0)for varying Pr ,Nb ,Nt ,S ,Nr ,Nc,λ1,θw&ΩT .

Table 3.Outcomes of-φ′(0)for varying Pr ,Nb ,Nt ,S ,Nr ,Nc,λ2,Le&Ωc.
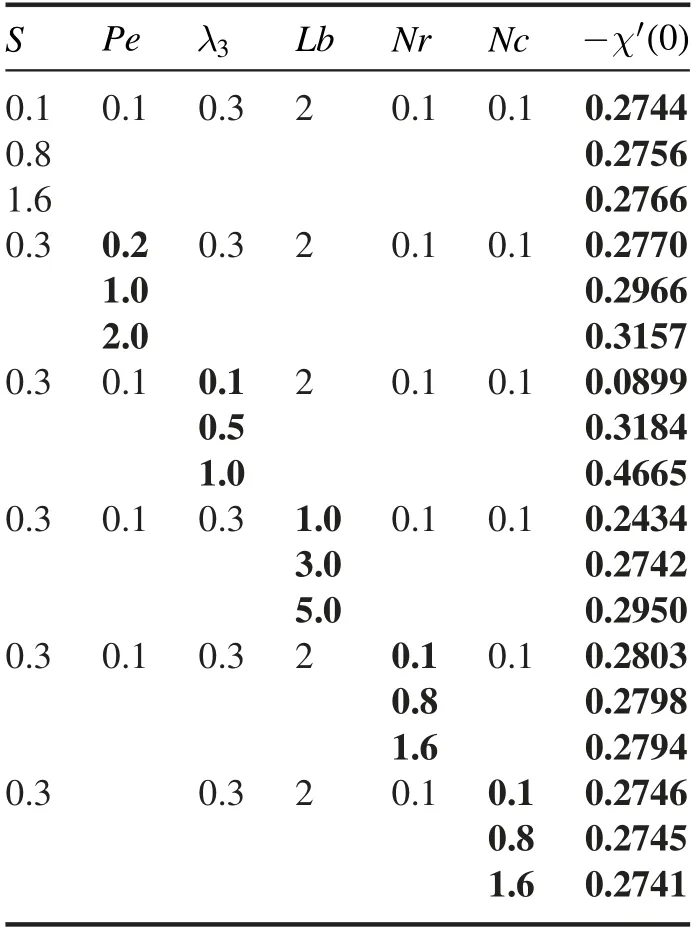
Table 4.Outcomes of-χ′(0)for varyingS,Pe,λ3, Lb,Nr and Nc.

Figure 12.Significance of Nt onφ.
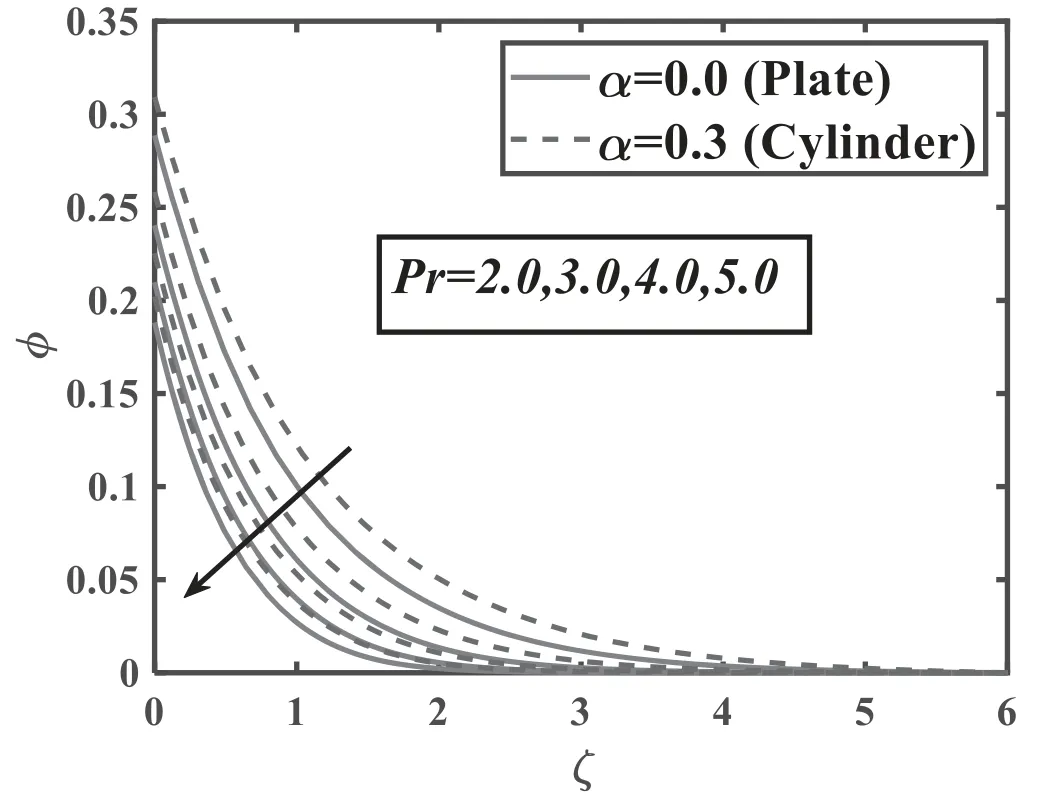
Figure 13.Significance of Pr onφ.
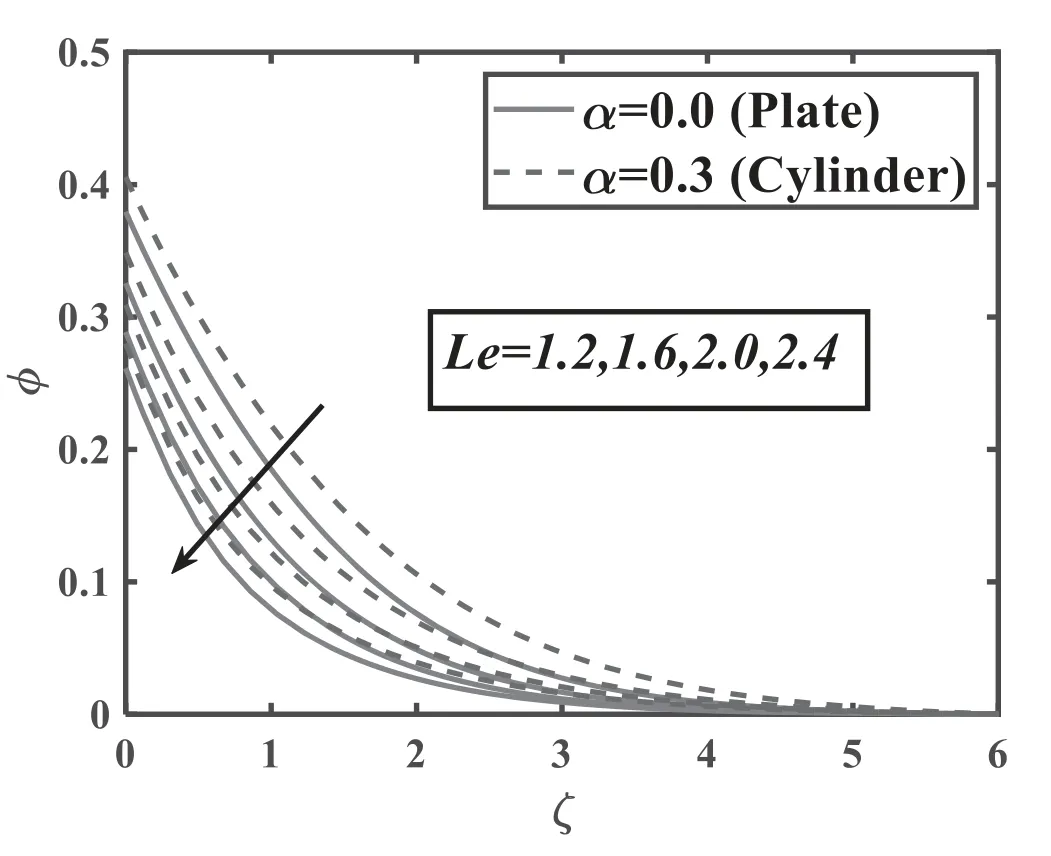
Figure 14.Significance of Le onφ.

Figure 15.Significance ofE onφ.

Figure 16.Significance ofλ2 onφ.

Figure 17.Significance of Ωc onφ.
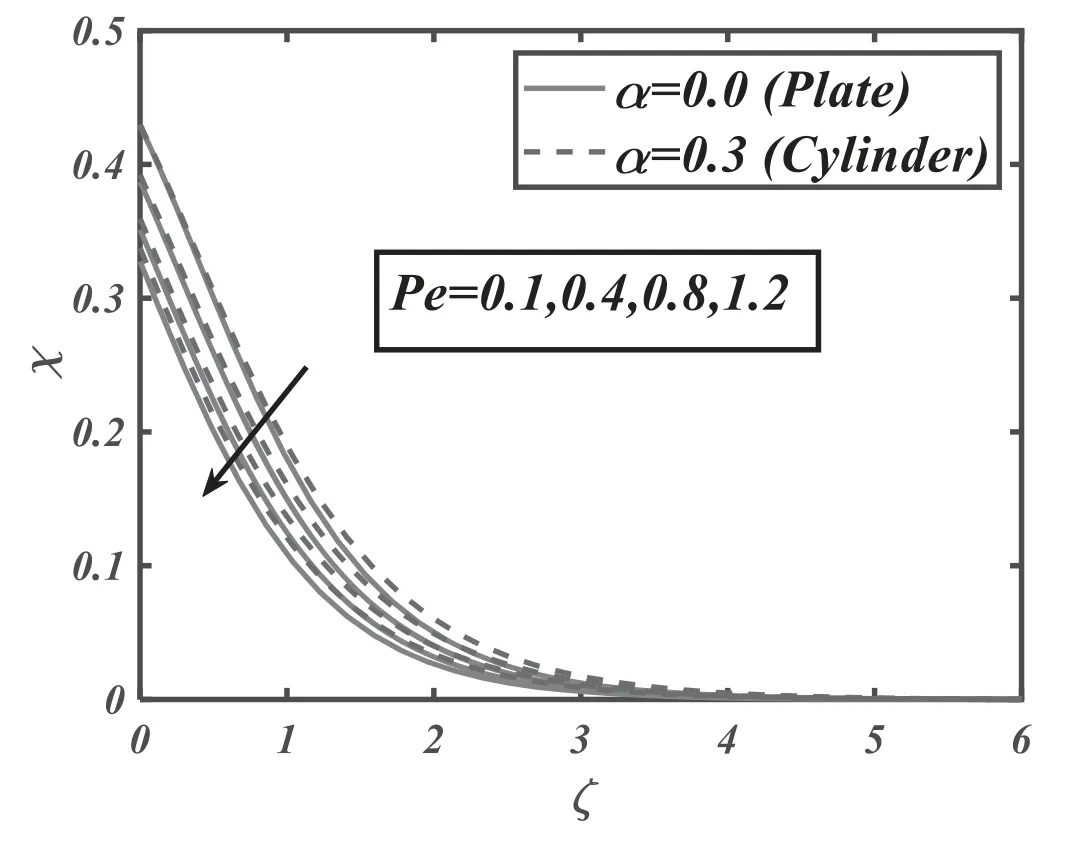
Figure 18.Significance of Pe onχ.
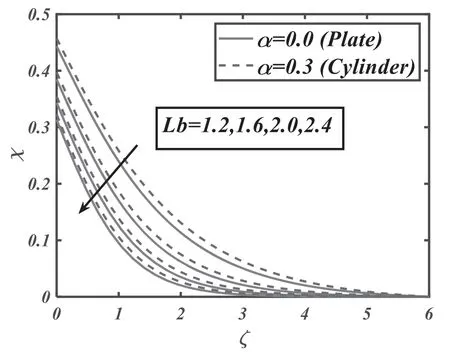
Figure 19.Significance of Lb onχ.

Figure 20.Significance ofλ3 onχ.
5.Conclusions
The flow of Newtonian nanoliquid by an inclined stretchable cylinder with the effects of motile microorganism and activation energy is discussed.The consequences of Cattaneo–Christov model are also considered.The velocity profile is declined by the mounting evaluation in the buoyancy ratio parameter and inclination parameter.The temperature field is reduced by intensifying values of thermal relaxation parameter and it shows growing nature for both thermal Biotnumber and temperature ratio parameter.The higher valuations of magnetic parameter and mixed convection parameter have reverse nature for velocity profile.Both temperature distribution and volumetric concentration fall for increasing values of the Prandtl number.The volumetric concentration field is boosted for swelling values of activation energy and thermophoresis parameter while show opposite behavior for Lewis number and concentration relaxation parameter.The growing evaluation of microorganism stratified Biot number boosted the motile microorganism’s concentration of nanoparticles.Bio-convection Lewis and Peclet numbers reduced the motile microorganism’s concentration of nanoparticles.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University,Abha,Saudi Arabia for funding this work through research groups program under grant number R.G.P-2/97/42.
杂志排行
Communications in Theoretical Physics的其它文章
- The relation between the radii and the densities of magnetic skyrmions
- Influences of flexible defect on the interplay of supercoiling and knotting of circular DNA*
- Understanding sequence effect in DNA bending elasticity by molecular dynamic simulations
- Influence of relative phase on the nonsequential double ionization process of CO2 molecules by counter-rotating two-color circularly polarized laser fields
- The upper bound on the tensor-to-scalar ratio consistent with quantum gravity
- Hawking radiation and page curves of the black holes in thermal environment
