Integrability of auto-Bäcklund transformations and solutions of a torqued ABS equation
2021-08-10XueliWeiPetervanderKampandDajunZhang
Xueli Wei,Peter H van der Kamp and Da-jun Zhang,∗
1 Department of Mathematics,Shanghai University,Shanghai 200444,China
2 Department of Mathematics and Statistics,La Trobe University,Victoria 3086,Australia
Abstract An auto-Bäcklund transformation for the quad equation Q11 is considered as a discrete equation,called H2a,which is a so called torqued version of H2.The equations H2a and Q11 compose a consistent cube,from which an auto-Bäcklund transformation and a Lax pair for H2a are obtained.More generally it is shown that auto-Bäcklund transformations admit auto-Bäcklund transformations.Using the auto-Bäcklund transformation for H2a we derive a seed solution and a one-soliton solution.From this solution it is seen that H2a is a semi-autonomous lattice equation,as the spacing parameter q depends on m but it disappears from the plane wave factor.
Keywords:auto-Bäcklund transformation,consistency,Lax pair,soliton solution,torqued ABS equation,semi-autonomous
1.Introduction
The subtle concept of integrability touches on global existence and regularity of solutions,exact solvability,as well as compatibility and consistency(see[1]).In the past two decades,the study of discrete integrable systems has achieved a truly significant development,which mainly relies on the effective use of the property of multidimensional consistency(MDC).In the two-dimensional case,MDC means the equation is consistent around the cube(CAC)and this implies it can be embedded consistently into lattices of dimension 3 and higher[2–4].In 2003,Adler,Bobenko and Suris(ABS)classified scalar quadrilateral equations that are CAC(with extra restrictions:affine linear,D4 symmetry and tetrahedron property)[5].The complete list contains 9 equations.
In this paper,our discussion will focus on two of them,namely
and
Here u=u(n,m)is a function onZ2,p and q are spacing parameters in the n and m direction respectively,δ is an arbitrary constant which we set equal to 1 in the sequel,and conventionally,tilde and hat denote shifts,i.e.
H2 is a new equation due to the ABS classification,while Q1δextends the well known cross-ratio equation,or lattice Schwarzian Korteweg–de Vries equation Q1δ=0.Note that spacing parameters p and q can depend on n and m respectively,which leads to nonautonomous equations.
For a quadrilateral equation that is CAC the equation itself defines its own(natural)auto-Bäcklund transformation(auto-BT),see[5].For example,the system
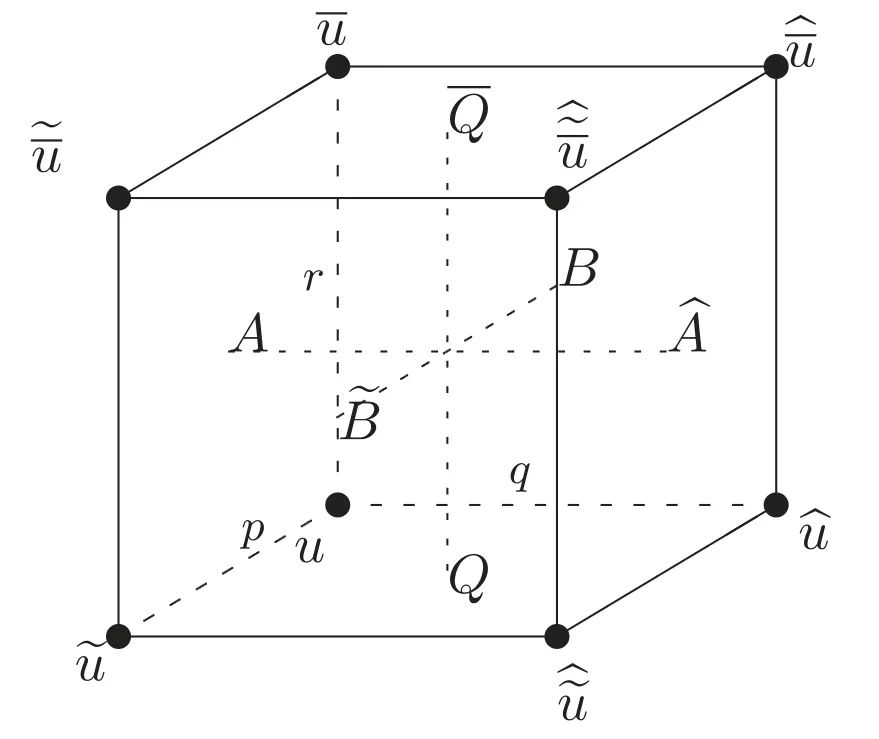
Figure 1.Consistent cube with equations A,B and Q on its faces.
where r acts as a wave number,composes an auto-BT betweenandSuch a property has been employed in solving CAC equations,see e.g.[6–10].
Some CAC equations allow auto-BTs of other forms.For example,in[11]it was shown that the coupled system
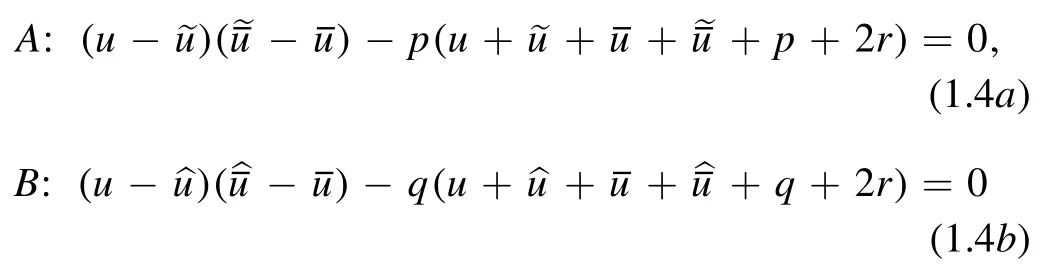
provides an auto-BT between
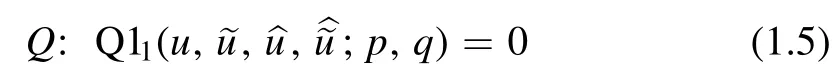
In[14]the auto-BT(1.4)and its superposition principle have been derived from the natural auto-BT for H2,employing a transformation of the variables and the parameters.The equation
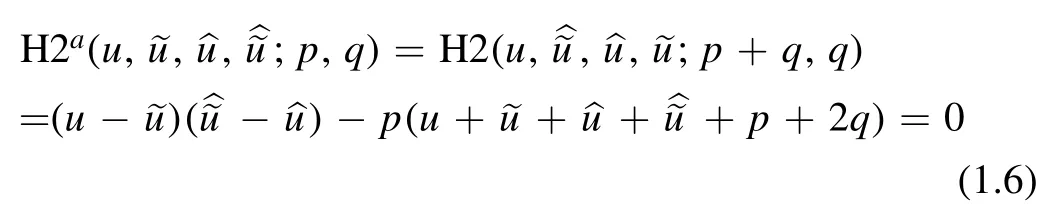
was identified as a torqued version of the equation H2.The superscriptarefers to the additive transformation of the spacing parameter.In[11],equation(1.6)appeared as part of an auto-BT for Q11.The corresponding consistent cube is a special case of[15,equation(3.9)].In[14],equation(1.6)was shown to be an integrable equation in its own right,with an asymmetric auto-BT given by A=H2a=0 and B=H2=0.Here we provide an alternative auto-BT for equation(1.6)to the one that was provided in[14].
In section 2,we establish a simple but quite general result,namely that if a system of equations A=B=0 comprises an auto-BT,then both equations A=0 and B=0 admit an auto-BT themselves.In particular,the equation H2agiven by(1.6)is CAC,with H2aand Q11providing its an auto-BT.We construct a Lax pair for H2a,which is asymmetric.In section 3,we employ the auto-BT for H2ato derive a seed-solution and the corresponding one-soliton solution.In the seed-solution the spacing parameter q depends explicitly on m,which makes H2ainherent semi-autonomous.Some conclusions are presented in section 4.
2.Auto-BTs for auto-BTs and a Lax pair for H2a
To have a consistent cube with H2aand Q11on the side faces,providing an auto-BT for H2a,we assign equations to six faces as follows:
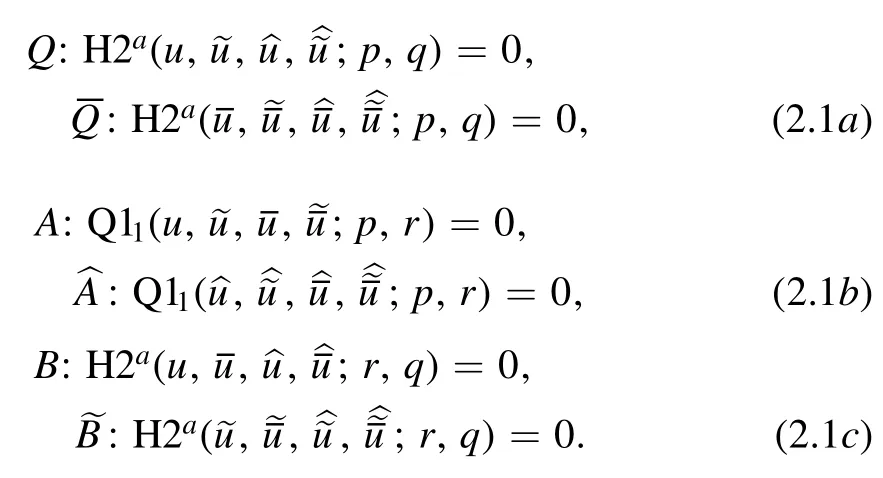
By means of such a consistency,the side equations A and B,i.e.
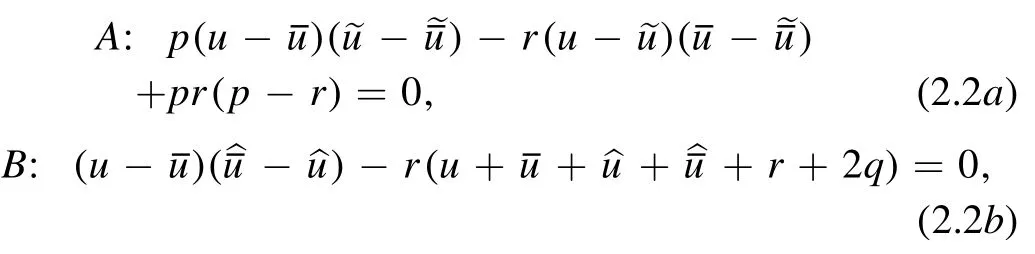
compose an auto-BT for the H2aequation(1.6).Here r acts as the Bäcklund parameter.
We note that the order of the variables in the equations(2.1)is quite particular.Since equation(1.6)is not D4 symmetric,i.e.we have
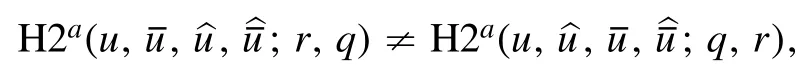
one has to be careful.The above result is explained by the following general result,see[16,section 2.1]where the same idea was used to reduce the number of triplets of equations to consider for the classification of consistent cubes.
Lemma 2.1.Let
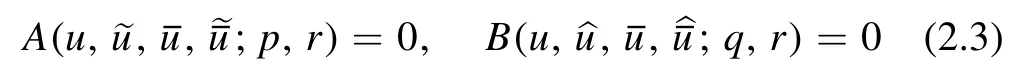
be an auto-BT for

Then we have(i)
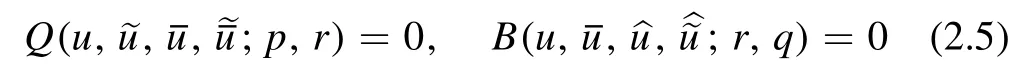
is an auto-BT for
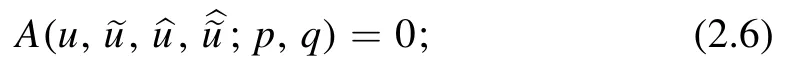
and(ii)
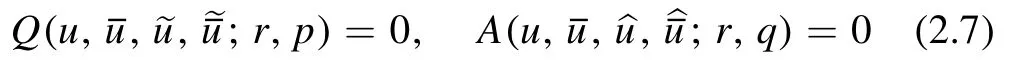
is an auto-BT for

Proof.IfA=B=0 is an auto-BT of Q=0,then they compose a consistent cube as in figure 1.We prove the result by relabeling the fields at the vertices,see[13,lemma 2.1].For(i)we interchangeandq↔r,and for(ii)we perform the cyclic shiftsandq→p→r→q.
Applying(i)to the consistent cube with(1.4a)and(1.5)we obtain(2.1a).Applying(ii)yields the same,as Q11has D4 symmetry.
3D consistency can be used to construct Lax pairs for quadrilateral equations(see[3,5,17]).To achieve a Lax pair for H2a,we rewrite(2.2a)as

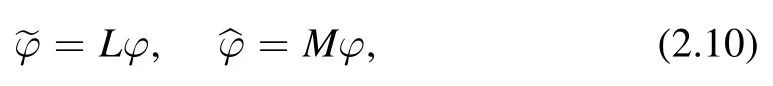
where
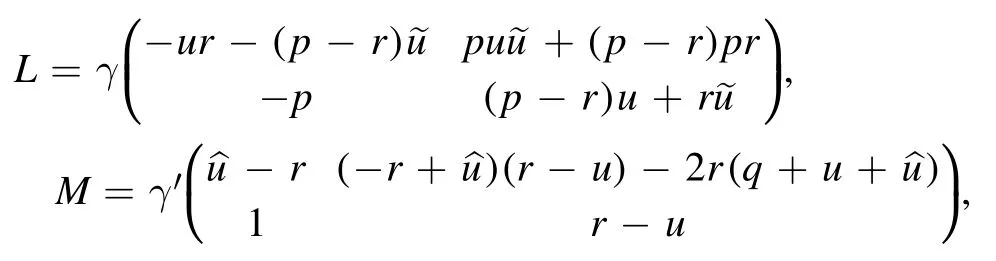
3.Seed and one-soliton solution
In this section,we use the auto-BT(2.2a)to construct solutions for(1.6).First,we need to have a simple solution as a‘seed’.To find such a solution,we takei n the BT(2.2a),i.e.
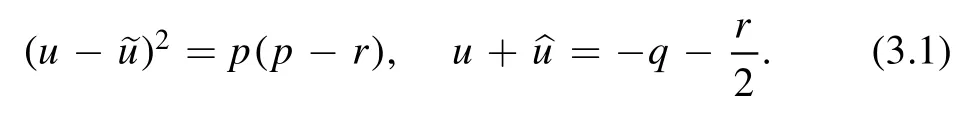
This so-called fixed point approach has proved to be effective in finding seed solutions[6,8].
Proposition 3.1.Parametrizing

and setting the seed BT parameter equal to r=c,the equations(3.1)allow the solution
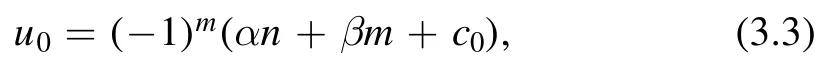
where c0is a constant.
Proof.By direct calculation,with the given parameterizations the equations(3.1)read
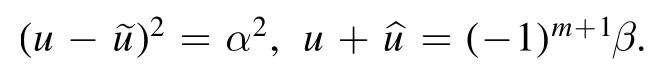
It can be verified directly that(3.3)also provides a solution to(1.6).Next,we derive the one-soliton solution for(1.6),from the auto-BT(2.2a)with u=u0as a seed solution.
Proposition 3.2.The equation(1.6),with lattice parameters(3.2)admits the one-soliton solution

where
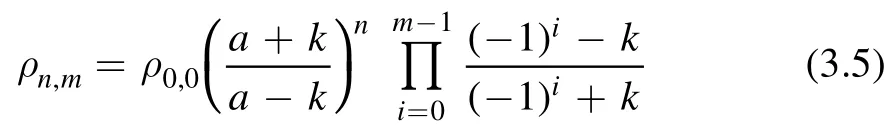
with constantρ0,0,is the plane wave factor.
Proof.Let
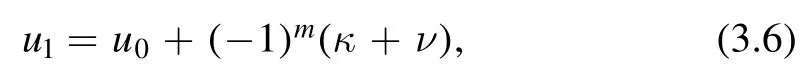
whereκ=kr.With(3.2)and parametrizing the first BT parameter by

then substitution ofu=u0andinto the auto-BT(2.2a)yields
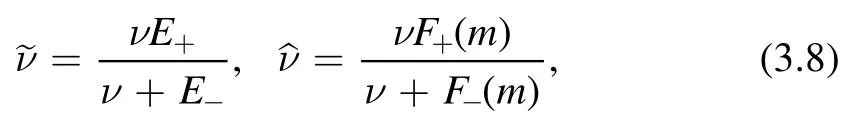
where

The difference system(3.8)can be linearized usingand φ=(f,g)T,which leads to
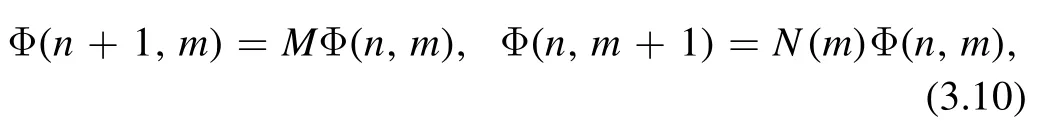
where

By‘integrating’(3.10)we have

where
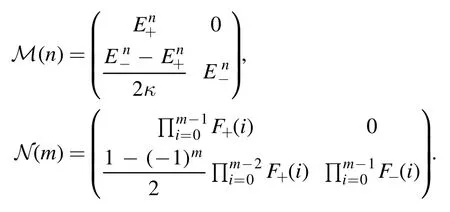
Thus,we get a solution to(3.12):
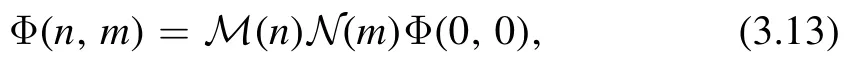
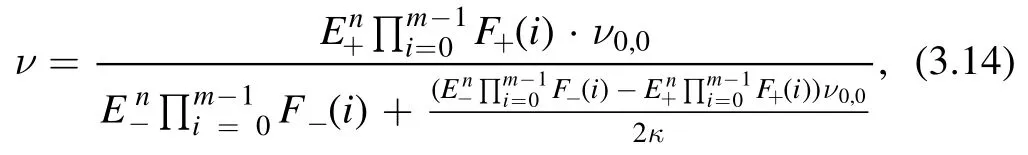
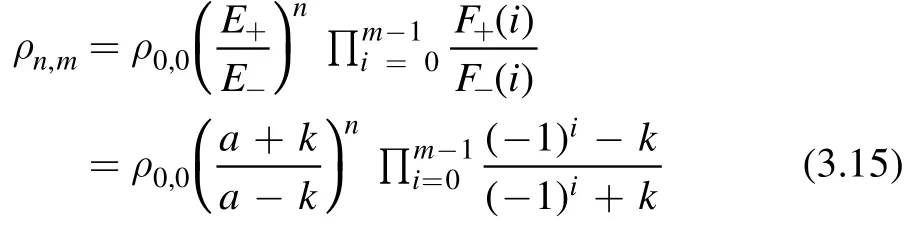
with constantρ0,0,the above ν is written as

where some constants are absorbed intoSubstituting(3.16)into(3.6)yields the one-soliton solution(3.4),which solves(1.6)with(3.2)and(3.7).Note that in the plane wave factor(3.15)n,m∈Z,and whenm≤0 the productis considered as
It is interesting that the solution has an oscillatory factor(−1)min m-direction and in the plane wave factor ρn,mthe spacing parameter q for m-direction does not appear.Considering the parameterization(3.2)where p is constant while q depends on m,we can say that the H2aequation(1.6)is semiautonomous.
4.Conclusions
In this paper,we have shown that equations which constitute an auto-BT for a quad equation admit auto-BTs themselves.We have focussed on one such equation,the torqued H2 equation denoted H2a(1.6),which forms an auto-BT for Q11.This equation is not part of the ABS list of CAC quad equations,as it is not symmetric with respect to(n,p)↔(m,q).The integrability of this equation is guaranteed as it is part of a consistent cube,see[14].The equations H2aand Q11comprise an auto-BT from which a Lax pair was obtained.Using this auto-BT we have derived a seed solution and a one-soliton solution.The parameterization of these solutions show that H2ais a semi-autonomous equation.We hope to be able to construct higher order soliton solutions in a future paper.
Acknowledgments
This work was supported by a La Trobe University China studies seed-funding research grant,and by the NSF of China[Grant Numbers 11 875 040 and 11 631 007].
杂志排行
Communications in Theoretical Physics的其它文章
- Influence of relative phase on the nonsequential double ionization process of CO2 molecules by counter-rotating two-color circularly polarized laser fields
- Deformation parameter changes in fission mass yields within the systematic statistical scission-point model
- Hawking radiation and page curves of the black holes in thermal environment
- The upper bound on the tensor-to-scalar ratio consistent with quantum gravity
- Influences of flexible defect on the interplay of supercoiling and knotting of circular DNA*
- The relation between the radii and the densities of magnetic skyrmions
