基于最小二乘回归的配变档位判别方法

云南电力科学研究院 覃日升 何 鑫 段锐敏 云南电网有限责任公司昆明供电局 何 觅

在电力系统中，配电网通过各种配电设施将电能分配给各类用电用户，配电变压器是配电网的源头，其对配电网的影响不可忽略。配电变压器所输出的电能质量受许多因素的影响，包括了配变档位、配变连接组别、负载率等，对这些因素进行科学分析，制定合理的处理措施，能够提高电能质量和电网运行的经济性。近年来随着用电用户数量不断增加，用电负荷的波动变化越来越快，电压波动也随之增加。部分地区用户在用电高峰时段电压偏低，个别地区“低电压”问题突出。同时，多数配电变压器档位在设置时通常仅凭经验一次设定，在运行中始终处于中间档位，未根据负荷变化情况进行调整，导致配电变压器出口电压不合格，造成用户电能质量不合格。

配电变压器档位能够影响到配电网的状态估计结果和后续的电压稳定分析，关系到电网调度人员对电网运行状态的判断和调度中心对电网的控制能力。让配电变压器处于合理的档位运行能够进一步降低配电网的能量损耗，更好地维持用户电压水平，保证电能质量。目前配电网中所装设的配电变压器大部分为无载调压装置，所采取的配变档位识别方式主要为人工离线校验，利用校验装置进行校验以及基于变压器绕组的在线识别。人工校验停电人工手动校验档位不仅流程繁忙且耗时耗力，利用校验装置来进行校验时存在触电风险且无法保证测量精度，工作量巨大、耗费人力，而基于绕组的在线识别容易在变压器正常运行时产生干扰，甚至可能损坏变压器，造成停电。

1 配电变压器调档

配电变压器调档是指调节变压器绕组的分接开关，从而改变了变压器的变比，以达到升高或降低变压器输出电压的目的。按调压方式可分为有载调压和无载调压。如图1所示，U1、U2分别为变压器一次侧、二次侧电压，N1、N2分别为变压器一次侧、二次侧绕组，变比为k。根据一、二次侧电压关系U1/U2=N1/N2=k推导可得U2=U1×N2/N1=1/k×U1，可看出调整变压器分接头的位置即改变了绕组的匝数N，从而改变了变压器的变比k，最终改变了输出电压U2。

图1 变压器绕组示意图

配电变压器调压的目的是为了给用户提供良好的电能质量，保证用户的电压始终处于合理的范围内。根据国家电能质量标准，标称电压为380V，线路末端用户电压水平不得高于标称电压的7%，即U2≤(1+7%)380V≈407V；不得低于标称电压的7%，即U2≥(1-7%)380V≈353V[1]。考虑到线路本身所带来的电压损耗，一般将配电变压器低压侧的电压设置为400V，即变压器高低压侧电压比为10kV/400V。为了调整输出电压U2，变压器的绕组要具有可调整的分接抽头，通过改变一侧绕组的线圈匝数，来改变变比k。一般配变常分Ⅰ、Ⅱ、Ⅲ、IV、V五档，出厂时一般置于ⅡI档，档位及对应电压等级（V）与档位范围(%)分别为：Ⅰ档420/+5，Ⅱ档410/+2.5，Ⅲ档400/0，Ⅳ档390/-2.5，Ⅴ档380/-5。

传统对配电变压器进行调档时，首先根据配变的参数和实际负荷情况进行初步计算，再根据计算所得到的结果来进行准确的、有针对性的调档，防止对设备甚至电网造成影响。目前电网所装设的配电变压器大多不能有载调压，在进行调档前要进行停电操作，如果调档前未做好充分的准备工作，未能做到准确调档，那势必需再次甚至多次调档、导致多次停电，对供电造成影响[2]。准确的在线档位识别可方便得到档位归属，为调档提供充足依据。

2 基于最小二乘回归的配变档位判别模型

因低压用户负荷波动不同，在识别配变档位时很难利用电流作为识别依据，建立回归模型时无法使用多元线性回归。配变出口电压因负荷变化会产生波动，可能造成某时刻电压超过档位范围，若仅利用峰值判断档位有可能造成误差，因此提出一种基于最小二乘回归的档位判别方法用以消除非正常电压对判别结果造成的影响。24小时电压曲线仅包含一个自变量、一个因变量，可用最小二乘回归处理。

2.1 数据预处理

采集配变数据时可能由于测量装置的异常等原因导致数据测量不完备，无法形成24点曲线，因此需对数据进行插值处理，拉格朗日（Lagrange）插值法常用来处理缺失点[3]，其定义如下：设有多项式函数(x0,y0),…(xk,yk),xj为自变量，yj为因变量，若多项式函数任意两个xj互异，则Lagrange插值多项式可表示为：。

2.2 最小二乘法回归分析

回归分析是指用一个或多个自变量来预测因变量的方法。最小二乘法回归（Least Squares Regression）是最简单的线性回归模型，也称为线性回归的基础模型，最小二乘回归可更广泛地应用于非线性方程中，它通过计算数据间最小误差平方和去寻找与之匹配的最佳函数[4]。利用最小二乘法可简便地求得未知的数据，并使得这些求得的数据与实际数据间误差的平方和为最小[5]。最小二乘法回归定义如下：

研究两个变量(x，y)之间相互关系时，往往会产生一系列数据对(x1,y1),(x2,y2),...(xm,ym)，这些数据描绘到x-y直系坐标中会分布在一条直线附近，令这条直线方程的表达式为=a0xi+a1(1)，其中a0,a1是任意的实数，最小二乘法是当自变量取值为xi因变量yi与回归方程所预测的之间差值平方最小，对于整个回归方程而言，就是所有预测值与实际因变量值之间差值平方之和最小。故可建立方程，式中V是关于a0,a1两个参数的函数，将式（1）代入可得。函数V分别对a0,a1一阶偏导求极值得式（2），对式（2）移项变换可得a0,a1两个参数关于xi,yi的表达式式(3)：

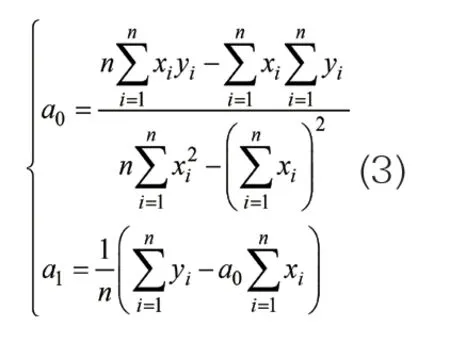
配变档位识别以电压量为基础，电压是随时间变化的数据对[(t1,u1),(t2,u2),...,(t24,u24)]，可用最小二乘法回归计算，得到一条实际因变量与所求数据之间误差平方和最小的直线，该回归直线可消除电压过高或过低的情况，使得电压分布在某电压档位附近，计算电压回归直线的均值结合配变档位选择即可进行归档。回归电压均值表达式为，式中是指各时刻回归电压，是指回归电压均值。

3 仿真验证

为验证本文所提档位识别方法的准确性，在PSCAD/EMTDC中搭建标准IEEE14节点系统模型。以图2模型中T-3变压器为例，测得其在不同负荷下变压器出口电压。

图2 标准IEEE14节点系统图

拉格朗日插值：因实际中24点电压曲线可能产生数据缺失情况，现仿真一天中随机2个小时数据缺失的情况，并对其采用拉格朗日法进行插值，得到插值前后对比如图3。

24点电压曲线最小二乘回归：配变出口电压一般随负荷变化产生波动，档位电压在实际采集中可能出现“坏点”，即非正常档位范围内电压值，现仿真I、II、III、IV、V五个档位24点电压曲线各三组，对各组插值后的电压曲线计算各自对应的最小二乘回归直线。从图4可看出，各个档位电压均波动较大，某些时刻的电压已超出档位范围，若以峰值判断档位可能造成误差。利用本文所提方法将24小时电压曲线进行最小二乘回归后，各时刻电压均落在对应的档位范围内，最小二乘回归可消除此类坏点，因此最小二乘回归更适用于档位识别。计算回归后电压均值与表1比较可直接进行档位归属。

图3 24点电压曲线拉格朗日插值前后对比

图4 三组5档24时电压曲线及最小二乘回归

三组数据各档位回归电压均值（V）分别如下：I档421.68/423.61/424.19，II档412.98/416.33/413.13，III档402.37/401.78/402.30，IV档391.65/391.12/394.35，V档380.73/380.34/381.64，三组数据各档位回归均值与配变档位匹配，可准确归属档位。