改进SURF和Delaunay三角网在图像匹配中应用*

毛克乐

(新乡学院 现代教育技术中心， 河南 新乡 453003)

随着现代科学技术的飞速发展，图像匹配技术在当代信息处理领域中显得愈来愈重要.图像匹配主要针对多个不同传感器或者不同时段等对同一场景拍摄下来的两幅图像，寻找图像间的共有区域以确定图像间的平移旋转关系，然后进行配准/匹配的过程.鲁棒性、精确性和稳定性是衡量图像匹配算法性能的重要技术指标，如何提高图像配准的精度和效率一直都是图像配准技术研究的核心问题.

2006年，Bay等[1]在SIFT(scale invariant feature transform)基础上提出SURF(speeded up robust feature)算法提取图像特征点.该算法不仅匹配速度快而且具有更高的稳定性和可移植性，相比局部特征的SIFT算法，其速度要快3倍左右[2]，因此，是目前主流匹配方法之一.但是SURF算法在匹配时仅考虑特征向量间的欧氏距离，丢弃了大量数据本体的结构信息，当图像噪声大、相关信息模糊时，错误匹配点数明显增大.针对这个问题，文献[3]提出M估计法对匹配矩阵进行预估计，但是M估计严重依赖由线性最小二乘估计获得的初始矩阵，精度和稳定性都比较差.文献[4]提出一种利用Kd树先把样本空间划分后再进行最近邻查询法，但是这种方法在构建Kd树索引结构时，计算代价比较高.文献[5]提出在SURF算法基础上引入颜色信息来改善SURF算法，在特征点提取时引入图像颜色信息和图像全局信息来对特征点进行描述，弥补了SURF的不足，但是匹配效果仍然不理想.文献[6]提出在SURF的基础上采用RANSAC对匹配点对进一步提纯，RANSAC是一种通过对观测数据进行全局鲁棒性参数估计的方法，但是该方法需要反复迭代，以获取最优代价函数模型，因此，计算代价大且结果可能并非最优.文献[7]提出一种利用子块的三角特征与对角特征的SURF机制和Delaunay三角剖分法的图像匹配方法，虽然该方法具有良好的鲁棒性，但是特征点稀疏导致匹配效果并不理想.文献[8]提出一种引入颜色不变模型的SURF和Delaunay三角剖分法的图像匹配法，虽然该方法有效保留了图像颜色信息，增加了特征点数量，但是却忽略了因引入颜色不变模型所带来的特征点过于密集、错误匹配点对增大的影响，大大降低了后续Delaunay三角剖分的匹配精度与效率.本文提出一种改进的基于SURF和Delaunay三角网格的匹配方法.首先引入颜色不变模型对两幅图像进行预处理，保留图像颜色信息以弥补SURF特征点检测不足的影响；其次通过SURF算法提取图像特征点集，并利用邻近特征点之间的关系初步剔除错误匹配对，解决特征点过于密集问题；然后对两幅图像分别进行Delaunay三角剖分获得两幅图像的Delaunay三角网，通过相似性判断，根据经验值选择相似度大于0.75的三角形对作为候选配准三角形对；接着通过射影不变量分析剔除错误匹配对；最后通过空间变换处理实现两幅图像的最终精确匹配.本文方法有效克服了文献[7-8]的缺陷，具有较强的鲁棒性和匹配精度.

1 改进的SURF算法

1.1 颜色不变量模型

Bannert等[9]在Kubelka-Munk理论基础上提出颜色不变量模型.Kubelka-Munk理论的光度发射模型为

E(λ，x)=μ(x)(ρf(x)+(1-ρf(x))2R∞(λ，x))

(1)

式中：x为图像的二维平面位置；μ(x)为位置函数；λ为波长；ρf(x)为在x处的Fresnel反射系数；E(λ，x)为光谱反射的成像结果；R∞(λ，x)为反射率.通过对式(1)进行微分和二次微分处理可得

(2)

(3)

根据式(2)、(3)可以得到一系列颜色不变量的描述子，即

(4)

式中：Hi为光谱强度为i时的颜色不变量；mx为位置x处时纵坐标上的特征点数；n和m为选取的横纵坐标特征点数.

(5)

本文选择的颜色不变量描述特征为：Eλy、Eλx、Eλλx、Eλλy、Eλ、Eλλ，根据式(6)可以求得颜色不变量为

(6)

1.2 SURF特征点检测

SURF是一种非常优秀的局部特征点检测和描述算法，对图像的几何变换、光照等具有很好的不变特性.将上文计算得到的颜色不变量H作为输入，采用箱式滤波器[10]取代二阶高斯微分.通过不断增大箱式滤波器的窗口大小构建不同的图像尺度空间，并采用积分图[10]提高计算速度.取空间图像中任意一个点X(x，y)，尺度为σ，Hessian矩阵H(X，σ)定义为

(7)

det(H)=DxxDyy-(0.9Dxy)2

(8)

差分图像中得到Hessian矩阵行列式的响应图像后，需要设置一个阈值，当式(8)大于这个值时，对该点对应的3×3×3三维空间邻域内的所有点作非极大值抑制处理，将大于临近26个响应值的点作为备选特征点，然后在图像空间和尺度空间采用线性插值法得到稳定特征点的精确位置值.

1.3 SURF改进预处理

考虑到由于引入颜色不变量模型，虽然保留颜色信息成分，但是同时会导致引入更多的冗余和错误匹配对并且会明显增大后续Delaunay部分的计算代价.因此，在执行Delaunay三角剖分之前先利用邻近特征点之间的关系，对SURF检测到的预匹配点对进行预处理，剔除部分冗余和错误匹配对，剩下的数据作为Delaunay三角剖分的输入.具体剔除原理为：设(Pi，Qi)和(P′i，Q′i)是两幅图像上的正确匹配点对，则Pi和P′i的距离d(Pi，P′i)应该与Qi和Q′i的距离d(Qi，Q′i)相似.根据这一关系提出以下评价函数，即

(9)

2 Delaunay三角剖分与匹配

2.1 Delaunay三角剖分

Delaunay三角剖分在代数拓扑学中是一种采用拓扑结构精确衡量离散点集之间几何关系的一种基本方法[11].本文采用SURF算法优化后获取的点集作为给定的离散点集，剖分得到Delaunay三角网格结构，并且该结构具有不重叠性和唯一性.Delaunay三角剖分满足最小角最大准则和空外接圆准则.本文主要由逐点插入法构建Delaunay三角网格，同时采用局部优化提升网格质量、三角形相似函数对三角网格判断和射影不变量处理三部分引入到Delaunay三角剖分中.

2.2 构建Delaunay三角网格

逐点插入法是Lawson提出的用于构建Delaunay的基本方法[12]，具体步骤如下所示：

1) 创建一个涵盖所有离散点的超大三角形作为初始三角网；

2) 在离散点集中随机选取一个点，然后在初始三角网中插入该点；

3) 把该点与初始三角网的三个顶点连接，生成三个小三角形；

4) 利用Lawson的LOP优化算法，对所有三角形逐个更新[13-14]；

5) 重复步骤2)～3)，直到插入所有离散点；

6) 删除包含有初始三角网定点的三角形.

2.3 Delaunay三角形相似函数判断

Delaunay三角网格中任意两个对应的三角形相似性可以根据三角形模糊相似度方法进行判断[15].

在两幅图像上的Delaunay三角网格中随机取一对相似三角形分别记为△ABC和△A′B′C′，且两个三角形的三个定点分别依次对应.取A角值为a，A′角值为a′，则对应相似度为

(10)

通过式(10)分别求取该相似三角形对的另外两对顶点的相似度值Ib、Ic，则这对三角形的相似度为

I=(Ia+Ib+Ic)/3

(11)

通过式(10)、(11)分别计算两幅图像中Delaunay网格所有三角形的相似函数，同时把得到的相似度值写入一个M×N(M、N分别为两个Delaunay三角网格中三角形的个数)的相似度矩阵中，并找出相似度大于0.75的三角形对.

2.4 射影不变量精匹配

根据Delaunay三角网格结构的不重叠性和唯一性可知，在Delaunay三角网格中每个共线相邻三角形最多有3个，如图1所示.通过这些不变量剔除SURF预处理后剩下的错误匹配对.选取尺寸为232×223像素的玫瑰花，以点对A和A′为例，若它们满足式(12)则表示为正确匹配点对，否则为错误匹配点对.处理结果如表1所示.

(12)

图1 三角形及其对应三角形Fig.1 Triangles and their counterparts

表1 三角网格处理结果Tab.1 Result of triangular meshing process

2.5 改进匹配算法流程

针对传统SURF算法颜色信息丢失问题引入颜色不变模型，同时利用邻近特征点之间的关系克服因颜色不变量模型而导致的错误匹配对增加问题，最后利用Delaunay三角剖分法作精确匹配处理，详细流程如图2所示.

3 实验和结果分析

本文实验硬件环境为Intel i3 CPU，6 GB内存，实验软件环境为Win10操作系统下Visual-Studio2015+OpenCV2.4.9编程工具，实验数据为232×223像素的玫瑰花.

图2 匹配算法流程Fig.2 Flow chart of matching algorithm

3.1 算法鲁棒性分析

本文首先通过对测试图像进行椒盐噪声+旋转+尺度变换处理以测试图像匹配算法的鲁棒性能.依次利用文献[7-8，16-17]以及本文算法进行图像匹配测试.不同算法的匹配效果如表2所示.从表2中可以看出，本文算法具有更好的鲁棒性和匹配效果.

首先分析只加入噪声处理的五种方法匹配对比效果.表2中，从利用文献[7]匹配算法处理加入椒盐噪声的图片可以明显看出存在错误匹配对，并且特征点稀疏匹配效果不理想，正确匹配率约为89.5%；文献[8]匹配算法的匹配结果看不出明显的错误匹配点对，且检测的特征点多，分布也比较均匀，匹配结果符合文献[8]所述，既保留了图像的颜色不变量信息，又有效提高了匹配效果，正确匹配率为94.1%，但是其计算代价明显增加.文献[16]匹配算法从匹配效果上可以看出特征点数较文献[8]明显减少，正确匹配率达到95.1%，效果良好；文献[17]的匹配特征点数最少，匹配效率较文献[16]有一定提升.从本文算法匹配效果可以看出，匹配效果良好，无明显错误匹配对，正确匹配率为96.2%，略高于文献[17]，特征点数介于文献[16]和文献[17]之间，分布也比较均匀.表2中的绿色圆点为本文算法相比文献[8]所剔除的点，既保留了图像颜色不变量信息，又有效避免了文献[8]的计算代价缺陷.因此本文算法鲁棒性更强.

接着分析五种算法对加入椒盐噪声并旋转处理的图片处理效果.单从图像匹配结果上看，五种方法都不存在明显的错误匹配，但是由于文献[7]方法忽略了图像颜色不变量信息，导致其特征点数依然很稀少，文献[8]检测到的特征点数非常丰富且分布均匀，而本文方法所检测到的特征点数依然位于两者之间，效果较两者都比较好.文献[16-17]匹配效果和本文相当.

最后分析五种算法对加入椒盐噪声+旋转+尺度变换处理的图片匹配效果.由表2可以看出，文献[7-8，16]三种方法匹配效果都存在比较明显的错误匹配对.文献[17]采用基于梯度角度的直方图局部特征描述子，虽然有效克服了旋转与尺度变换的影响，但是以牺牲有效特征点为代价，在图像噪声大的环境下效果很差.本文方法在有效剔除错误匹配对的同时保留了绝大多数有效特征点，效果表现良好.表2中五种方法匹配正确率分别如表3所示.正确匹配率随着加入干扰的复杂度逐渐降低，虽然对于只加入椒盐噪声及椒盐噪声+旋转的两组图片匹配点对数变化不大，但是椒盐噪声+旋转+尺度变换后，检测的匹配点对数明显减少.因此，干扰越复杂，匹配点对数越少，正确匹配点对数也相应变少.

表2 五种算法匹配对比Tab.2 Matching comparison of five algorithms

表3 五种方法针对不同图像的匹配精度Tab.3 Matching accuracy of different images obtained by five algorithms

3.2 计算代价分析

为了衡量三种算法的计算代价，本文从百度图库下载10幅分辨率为232×223像素的图片并分别进行噪声和旋转处理构成10组测试数据，测试结果如图3所示.可以看出文献[8]因为引入图像颜色不变量模型导致SURF特征点检测数过于密集，对于后期Delaunay三角网构建非常困难进而导致计算代价增加.文献[7]因为没有考虑图像颜色不变量信息，因而特征点检测数量稀疏，计算代价最小，所以时间最快.文献[16]和文献[17]均保留了传统SIFT算法的优点，但文献[16]没有考虑SIFT计算代价高这一缺点.本文方法在考虑颜色不变量信息的同时利用邻近特征点之间的关系解决文献[8]缺陷，同时既保留了图像颜色不变量信息，又降低了算法计算代价.由图3可以看出，本文算法时间与文献[7]相当.五种方法匹配正确率均值如图4所示，从整体上看，本文算法匹配正确率最佳，文献[8，17]效果较本文算法略差，文献[7，16]效果最差.

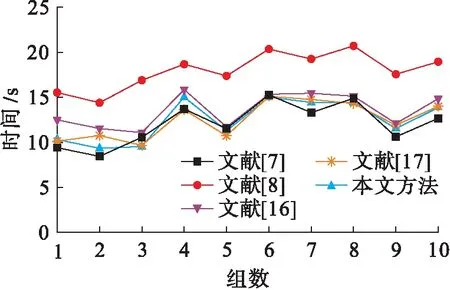
图3 五种方法计算时间Fig.3 Calculation time of five algorithms

图4 五种方法匹配正确率Fig.4 Correct matching rate of five algorithms

4 结 论

本文针对基于SURF+Delaunay三角剖分图像匹配算法忽略图像颜色不变量信息以及由于引入颜色不变量模型后特征点过于密集而导致后期Delaunay三角剖分处理困难问题，提出在SURF算法和Delaunay三角剖分算法之间加入利用邻近特征点之间的关系解决特征点过于密集问题的方法.兼顾匹配效率与匹配精度，在实际应用中具有良好的应用效果.后期将进一步研究在原有基础上加入分区域处理，探究相邻区域之间的临近特征点关系.