关于我国人均消费支出的计量经济学分析
2021-08-09苏毓倩
苏毓倩


摘要:改革开放以来,经济社会繁荣发展,人民生活水平显著提高,除基本的生存资料消费外,人们更加注重发展资料消费、享受资料消费等此类提升素养,修养身心的消费。文章通过分析2019年我国31个省、市、自治区的人均消费支出数据,建立合理的计量经济学模型来探究影响我国消费支出的主要因素并提出行之有效的消费建议。
关键词:消费;支出;收入;计量经济学;异方差
研究表明,在接受教育后,有人获得51%~91%的回报,而有人却只收获-32%的负回报,为什么有如此悬殊的差异? 这就要考察教育回报率到底受哪些因素影响。笔者通过分析工资、年龄、教育年限等数据建立合理的计量经济学模型来探究教育投资回报率的影响因素并提出行之有效的建议。
一、假说与模型
改革开放以来,经济社会繁荣发展,人民生活水平显著提高,除基本的生存资料消费外,人们更加注重发展资料消费、享受资料消费等此类提升素养,修养身心的消费。为探究将我国人均消费支出的影响因素,通过文献分析,将人均消费支出(Y)、人均可支配收入(X1)、人均政府消费支出(X2)纳入模型,提出假设:居民人均可支配收入代表地区居民经济实力。地区居民人均可支配收入高,该地居民的生活水平高。则人均可支配收入与人均消费支出呈正相关关系;政府消费支出使得居民以免费或较低的价格获得货物和服务,则人均政府消费支出与人均消费支出负相关。
本文研究的数据为含有定性变量的截面数据。为了构造数学模型和计量经济学模型,通过偏回归散点图,初步确定模型。
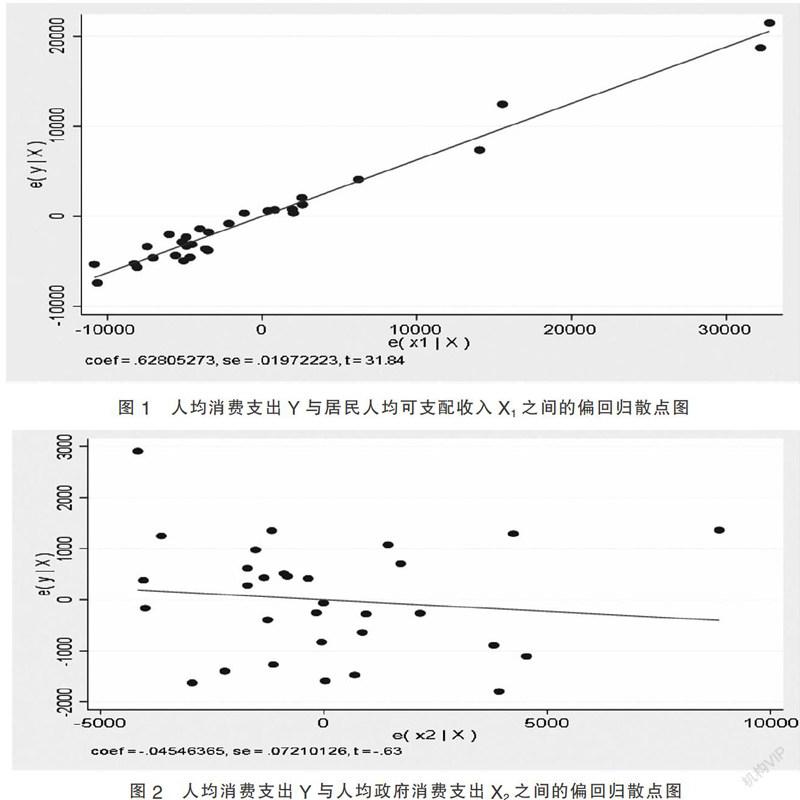
图1为人均消费支出Y与居民人均可支配收入X1之间的偏回归散点图。从该散点图可以看出Y与X1之间是呈现线性正相关,基本形式是一条直线,而且散点相对较集中于一条直线的附近;图2为人均消费支出Y与人均政府消费支出X2之间的偏回归散点图。与图1不同,该散点图看出Y与X2之间呈现线性负相关,基本形式是一条斜向下的直线。
根据假说与上述绘图分析结果,基本满足线性分布条件,设立如下多元线性回归数学模型:
Y=β0+β1X1+β2X2
考虑到被解释变量Y受诸多随机因素影响,故引入随机干扰项μ,构建如下多元线性计量经济学模型:
Y=β0+β1X1+β2X2+μ
二、统计分析
(一)数据回归分析
使用最小二乘估计法,模型估计结果如下:
Y^=2513.123+0.6280527X1-0.0454637 X2
(4.22) (31.84) (-0.63)
R2=0.9767 R2=0.9751 F=587.39
β置信区間如下:
β0的95%置信区间为[1294.166,3732.08]
β1的95%置信区间为[0.0876536,0.6684519]
β2的95%置信区间为[-0.1931564,0.1022291]
(二)模型检验
1. 经济意义。β1估计值为0.6280527,绝对值是在0~1之间的一个数,表示人均政府消费性支出和其他因素不变的条件下,人均可支配收入增加1元,人均消费支出增加0.6280527,与理论期望值相符,吻合基本假设;β2估计值为-0.0454637,是在0~1之间的一个数,符号为负,表示在人均可支配收入和其他因素不变的条件下,人均政府消费性支出增加1元,人均消费性支出减少0.0454637,与理论期望值符合,符合基本假设。
2. 拟合优度。用R2来进行拟合优度的检验,剔除了变量个数对拟合优度的影响,真实实现解释能力的增加。R2为0.9752,即Y变动的97.52%可由人均可支配收入和人均政府消费性支出这两个变量来解释,拟合情况较好、变量选择较优。
3. 赤池信息准则和施瓦茨准则检验。当增加了人均政府消费支出X2这个解释变量之后,AIC和BIC由原来的527.3371和531.6391分别变为了525.7742和528.6422,AIC和BIC都比原来的值有所降低,说明增加的X2可以有效地改善模型,故相比一元模型,选用二元线性回归模型更优。
4. 模型方程显著性检验。p=0.000,原方程总体上线性关系显著成立。
5. 变量的显著性检验。p=0.000通过检验,而p=0.533未通过检验。基于此认为人均消费支出与两个解释变量间总体线性关系显著,X1前的参数估计值通过显著性t检验,但X2前的参数估计值未能通过t检验。
t值为什么偏误?首先,考虑到估计的S可能出现偏误,导致t检验出现错误。其次从经济现象宏观角度分析,认为不同省份之间的人均消费支出差别主要来源人均收入,但由于不同地区发展情况不同,收入也不尽相同,因此怀疑X1的存在引起了异方差性,从而导致t检验失效,同时也不排除政府消费支出X2的差异引起的异方差性。最后,由于截面数据样本,造成大概率存在异方差性。
三、异方差的检验与修正
(一)检验
首先,借助导出残差平方项,绘制散点图:散点具有明显的扩大趋势,异方差可能存在,且为递增型。此外,e与X2的变化呈复杂形式,进一步验证可能存在异方差。
其次,B-P检验假定该函数为线性函数:μ2=δ0+δ1X1+δ2X2+ei,在校验过程中,虽然检验未通过,但由于μ2与X1、X2可以是其他非线性关系,不一定呈线性,故B-P检验存在缺陷,暂无法得出异方差不存在的结论。
最后,通过怀特检验:P值落入拒绝域,模型存在异方差性。由于怀特检验是对既无需先验信息,又照顾到解释变量交叉项与平方项等各种形式(线性或非线性),检验结果具有说服力,据此得出模型确存在异方差性。
