基于贝叶斯网络的地铁牵引系统可靠性评估

程岳梅 李小波 田世贺 陆朱剑

摘 要： 牵引系统身为地铁车辆的关键系统之一，提升其可靠性对于改善整个地铁车辆的可靠运行尤为重要。但是，牵引系统的结构复杂，且失效模式多样，采用传统的可靠性分析方法较为困难。针对这一问题，提出了一种基于贝叶斯网络的系统可靠性评估方法，并结合故障树法，对地铁车辆牵引系统的可靠性进行建模和分析。以某地铁牵引系统为例，利用贝叶斯网络模型计算出牵引系统的可靠度;通过贝叶斯网络的双向推理能力，找出对牵引系统可靠性影响最大的组件，即牵引系统的薄弱环节（IGBT反馈故障）。该方法的评估结果合理、准确，可为地铁车辆牵引系统的可靠性评估、故障诊断提供一定的理论参考。

关键词： 地铁车辆;牵引系统;可靠性分析;故障树;贝叶斯网络

文章编号： 2095-2163（2021）03-0056-05 中图分类号：U270.38;TP202+.1 文献标志码：A

【Abstract】The traction system is one of the key systems of subway vehicles， and improving its reliability is particularly important for improving the reliable operation of the entire subway vehicle. However， the structure of the traction system is complex and the failure modes are diverse， so it is difficult to adopt traditional reliability analysis methods. Aiming at this problem， a system reliability assessment method based on Bayesian network is proposed， combined with fault tree method， to model and analyze the reliability of metro vehicle traction system is modeled and analyzed. Taking a subway traction system as an example， use the Bayesian network model to calculate the reliability of the traction system; use the two-way reasoning ability of the Bayesian network to find the component that has the greatest impact on the reliability of the traction system， that is， the weak link of the traction system （IGBT feedback failure）. The evaluation results of this method are reasonable and accurate， which can provide a certain theoretical reference for the reliability evaluation and fault diagnosis of the traction system of subway vehicles.

【Key words】 subway car; traction system; reliability analysis; fault tree; Bayesian network

0 引 言

目前，地鐵车辆凭借自身的准时、运载量大、安全便捷、独立的运行环境等优点，已成为了大中型城市缓解交通拥堵的主要途径。地铁车辆是以人为载运对象的一种交通工具，因此，保障地铁车辆安全可靠地运行是重要前提。牵引系统作为地铁车辆的动力来源系统，在车辆运行期间，倘若出现由于牵引系统故障引发的各种故障形式，都有可能引发严重的交通安全事故，同时危及着出行市民的安全。因此，有必要评估地铁车辆牵引系统的可靠性，找到影响该系统可靠运行的薄弱环节，对指导牵引系统的维护检修以及进一步改善该系统的可靠性具有重大意义，从而保障地铁车辆的安全运行。

故障树分析法（fault tree analysis，FTA）是一种广泛、有效的系统可靠性分析方法。其中，林小松等人[1]就地铁牵引供电系统的常见故障，建立了相应的FTA模型，运用FTA法对牵引供电系统进行定性和定量计算;赵琼等人[2]引入重要度概念，通过分析接触网的故障机理，搭建其故障树模型，为技术人员对接触网的设计和维修提供理论依据;王炜俊[3]把FTA分析法运用到受电弓系统中，分析受电弓故障的最小割集以及计算受电弓可靠性评估指标，为受电弓的维护、设计提供参考;卫纬等人[4]通过搭建地铁车门系统的FTA模型，运用定性、定量分析方法，得出车门系统的故障模式和可靠性指标参量，为地铁车门的故障诊断、可靠性设计提供依据。上述的文献都可以运用故障树法，对某一个系统的可靠性进行评估分析。但是，对于识别系统的薄弱部分以及系统的不确定性现象，故障树法还不能很好地解决这些问题。由此可知，故障树法依然存在一些不足。然而，以数学理论为基础的贝叶斯网络（Bayesian network，BN）则可以有效地对此加以改进。比如，周巧莲等人[5]利用BN的优点，合理计算出了基本事件的后验概率，为了更进一步地评估车门系统，又引入灵敏度概念，从而为地铁车门的可靠性评估与故障维修提供参考;何江海等人[6]建立动态贝叶斯网络模型，运用在地铁牵引变电所中。从时间维度上对其进行可靠性分析，给后期的维护维修提供一定的参考价值。王佳培等人[7]鉴于接触网系统结构复杂而导致的子系统之间存在的不确定性问题，运用BN模型，对接触网系统进行可靠性分析。在此基础上，还列举出了几点关于改善该系统可靠性运行的建议;王宇等人[8]将FTA法与BN法结合，应用于地铁受电弓系统中，一定程度上解决了FTA法的不足之处。Liu等人[9]提出了一种从GO-FLOW模型到BN模型转化的一种新的方法。并且，以某一个系统为例分析，最后验证了该方法的可行性;古海龙等人[10]分析了采煤机系统的故障机理，考虑该系统存在的不确定问题，利用BN模型对其进行可靠性分析，为采煤机的可靠性设计提供理论依据;李兴运等人[11]结合模糊理论方法对贝叶斯网络进行改进，例证分析发现，该方法可以有效地改善系统的可靠性分析与建模能力。

因此，本文就BN模型在其他系统领域研究的基础上，结合故障树法，把BN法应用于地铁车辆牵引系统的可靠性评估中。在此基础上，利用现场调研得到的数据，建立其BN模型，进行可靠性分析。该方法不仅可以很好地解决故障树法在牵引系统评估中的局限性，而且能够准确合理地分析出牵引系统的可靠性指标参量，这样有助于指导维修人员更好地对牵引系统进行维修。

1 贝叶斯网络概述

贝叶斯网络[12]也称为信念网络（Belief Network），是一种以概率为理论基础，把复杂问题用图形表达出来的方法。BN的结构通常包含2个部分，也就是：有向无环图（Directed Acyclic Graph，DAG），是由变量节点和连接节点的有向边组成;根节点的先验概率（Priori Probability）和其他节点的条件概率表（Conditional Probability Table，CPT）。在实际工程应用中，系统的结构相对比较复杂，存在一定的不确定因素，难以准确推理出系统的可靠性指标参量。BN模型以自身的优点特性，对不定性、不确定信息问题有着很强的处理能力。因此，在系统可靠性评估等方面，BN模型在众多模型中脱颖而出。

假定用t来表示一个有向无环图，用i来表示有向无环图的所有节点集合，而用d来表示所有连接节点的有向边的集合，且令X={X1，X2，…，Xn}来表示某一个节点i代表的所有变量，则节点X的概率可表示为：

其中，pa（i）表示节点i的父节点，那么，就称X是相对于有向无环图t的贝叶斯网络。

根据BN模型给出的条件概率定义为：

其中，P（A|B）是后验概率，表示在事件B发生的条件下，事件A发生的概率;P（B）是先验概率，表示事件B发生的概率;P（B|A）是条件概率，表示在事件A已经发生的情况下，事件B发生的概率。

现假设某个事件A，有a1，a2，…，ai，…，an个不同值，两两互斥，通过全概率公式可得P（B）表达式为：

进而计算出后验概率P（A|B）。

鉴于BN模型节点之间的条件独立性，所以，在FTA法的基础上，建立的BN推理，就不必求解系统的最小割集，计算过程相对简单。同时利用BN的正向推断，能够计算出BN正常运行的概率，在某一个或几个变量节点给定的条件下;通过BN的反向推理，计算出某一个或几个变量节点的故障概率，在系统网络故障的情况下。通过BN模型的双向推理特性，可以识别网络的薄弱环节，对系统的可靠性评估有一定的作用。

2 基于故障树-贝叶斯网络的建模

2.1 模型基本关系转化

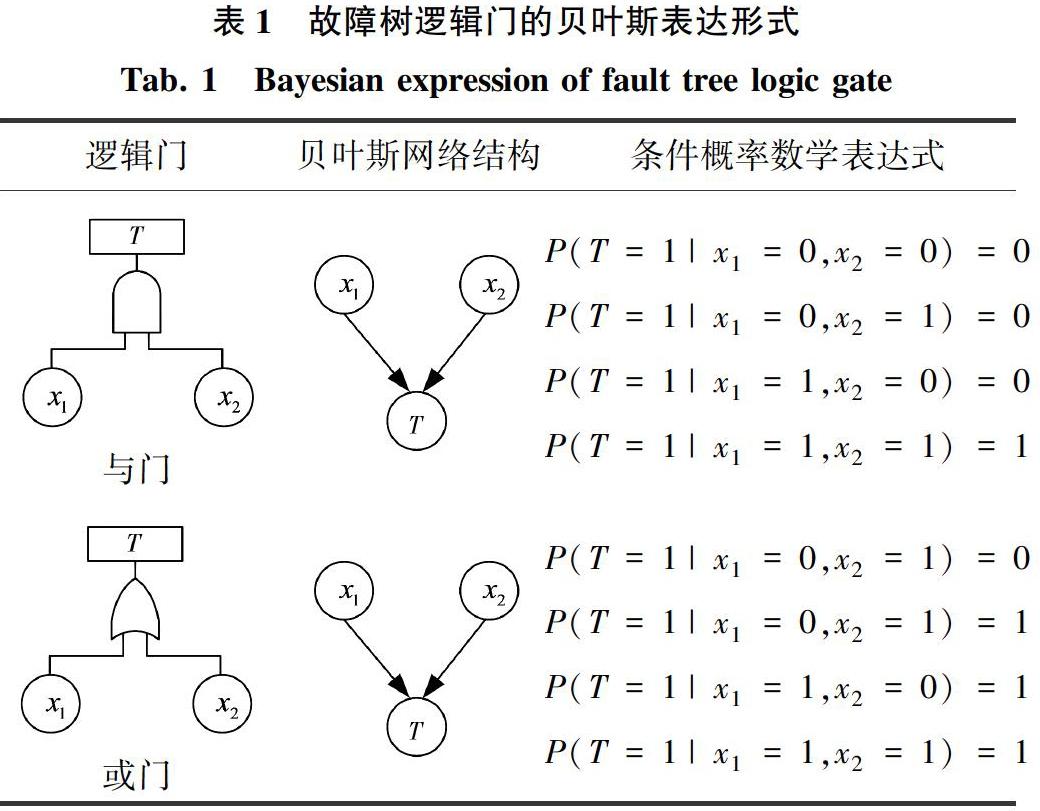
一般情况下，BN模型的建立是通过有向边和相应的条件概率分布来实现的，FTA模型是通过逻辑门连接各个事件。因此，为了实现FTA到BN模型的快速建模，这里有必要讨论FTA不同逻辑门所对应的BN表达形式。以下分别给出了FTA常用的“与门”、“或门”两种逻辑门的BN表达形式，见表1。

在表1中，条件概率数学表达式给出了子节点状态值为1的条件概率值，0是正常状态，而1是故障状态。

2.2 模型转化基本原则

从表1中可以看出，通过BN的条件概率，可以一一实现故障树的逻辑门关系。把故障树转化为BN模型，实现BN的建模，其转化过程遵循以下4点原则[13]：

（1）故障树中底事件发生的概率值赋给BN模型中根节点的先验概率。

（2）故障树中逻辑门的逻辑关系映射为BN模型中相应节点条件概率表，状态值与故障树中逻辑门的输出值一致。

（3） 故障树中的事件与BN模型中的节点一一对应。故障树中的底事件、中间事件和顶事件分别映射到BN模型中的根节点、子节点和叶节点，且多次出现的底事件，在BN模型中建立同一个根节点。

（4）故障树中表达的逻辑门关系，使用有向边连接BN模型中的节点，有向边的连接方向与故障树的逻辑门的输入输出关系一致。

3 实例分析

3.1 牵引系统故障树的建立

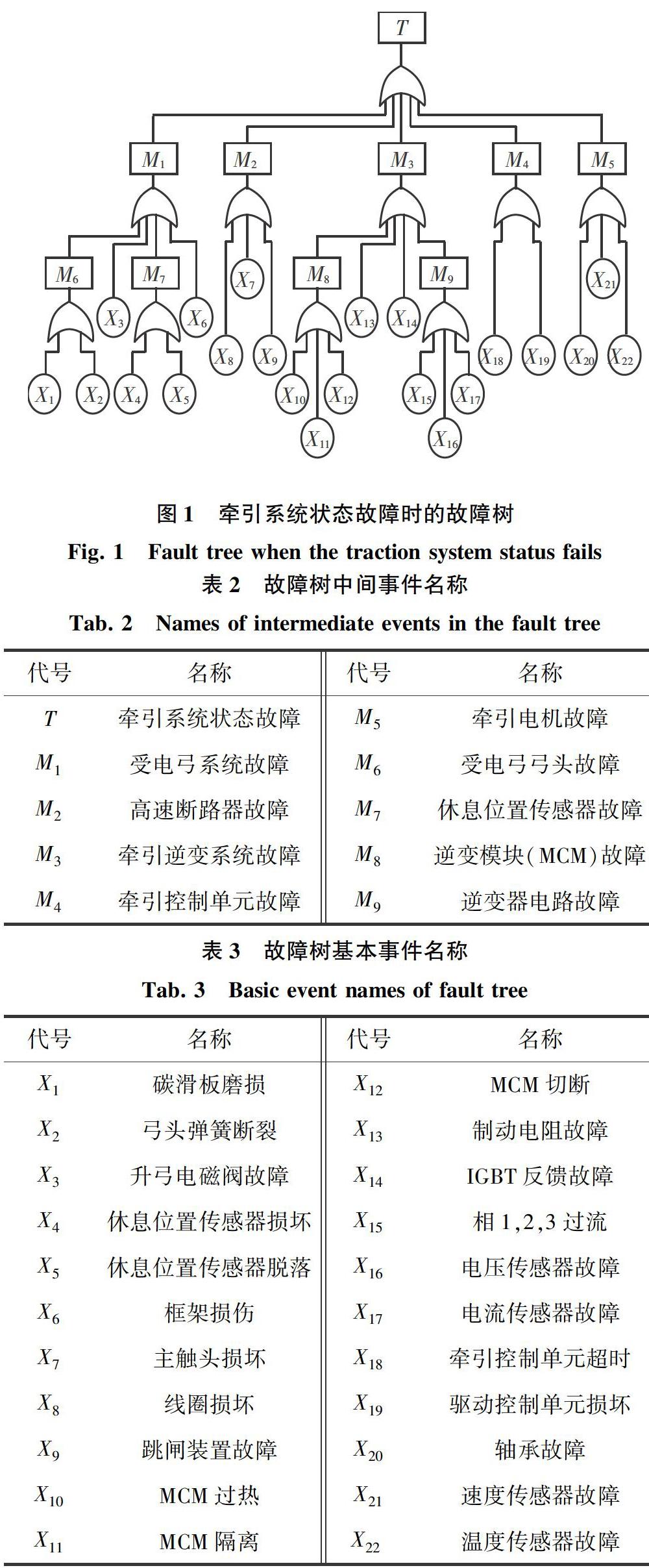
牵引系统的可靠性直接影响着地铁车辆运行的稳定性。本文的可靠性研究对象是某地铁的牵引系统，并以“牵引系统状态故障”为顶事件，搭建故障树。通过现场调研分析、收集相关的数据，统计得到牵引系统状态故障的原因主要包括：受电弓系统故障、高速断路器故障、牵引逆变系统故障、牵引控制单元故障和牵引电机故障。以上所述的5点原因均为中间事件，依据故障树建立的原则，搭建以“牵引系统状态故障”为顶事件的故障树。整个故障树共含有22个底事件，10个逻辑门和9个中间事件。如图1所示。

图1中，符号代表的各节点名称，故障树中间事件名称见表2、表3。

从图1中得知，顶事件通过“或门”与5个中间事件连接;4个中间事件通过“或门”與相应的中间事件、底事件相连。各个基本事件的故障概率，见表4。

3.2 牵引系统贝叶斯网络模型

按照前面故障树到BN模型的转化原则，建立牵引系统状态故障的BN模型，如图2所示，其中T，M1～M9是或门节点。

经计算，牵引系统状态故障事件发生的概率为：P（T=1）=0.147 7，由此可知，牵引系统的可靠性指标参量，可靠度R=0.852 3。

当牵引系统发生故障，各元件故障的条件概率，见表5。

为了直观清晰地看出每个元件的大小，系统中22个元件节点的条件失效概率曲线图，如图3所示。

从表5和图3可知，当牵引系统故障时所有元件节点的条件失效概率中，X14（IGBT反馈故障）、X1（碳滑板磨损）、X19（电流传感器故障）、X4（休息位置传感器损坏）、X18（牵引控制单元超时）的数值较大，即为牵引系统发生故障时较为薄弱的部分。

当牵引系统元件发生故障时，对应系统节点的条件故障概率，见表6。

从表6中可以发现，当不同元件故障时，系统节点故障的条件概率是不相同的，影响程度也就不一样。条件概率与元件对节点的影响程度呈正比关系。

综上所述，在实际应用中，根据具体情况，结合表5、表6，便可以确定牵引系统可靠运行的薄弱环节，为提高牵引系统整体的可靠性理论提供参考依据。维修人员平时对牵引系统进行日常维护工作时，重点关注X14、X1、X19、X4、X18这几个部件，在系统处于故障状态时，优先考虑上述部件进行故障排除，从而提高维护效率。

4 结束语

本文利用基于贝叶斯网络的系统可靠性分析法，结合故障树法，对地铁车辆牵引系统的可靠性进行评估，得到以下结论：

（1）本文将故障树法与BN结合，应用在地铁车辆牵引系统的可靠性评估中，克服了单一故障树法的局限性，不需要对系统的最小割集求解，计算过程相对也比较简单，很大程度上提高了可靠性分析的效率，分析结果合理准确。

（2）基于贝叶斯网络的地铁牵引系统可靠性评估，通过正向可靠性计算，得出了牵引系统故障发生时的概率为0.1477，即地铁车辆牵引系统的可靠度为0.8523;通过反向推理，求得了各个元件节点的后验概率，便于发现系统的薄弱环节，有利于维修人员更好地对牵引系统进行日常维护工作，对提高整个牵引系统的可靠性提供理论依据。

参考文献

[1]林小松，杨俭，袁天辰. 地铁牵引供电系统失效的故障树分析[J]. 城市轨道交通研究，2018，21（9）：26-31.

[2]赵琼，王思华，尚方宁. 基于故障树分析法的接触网可靠性分析[J]. 铁道标准设计，2014，58（1）：105-108，109.

[3]王炜俊. 基于故障树法的城市轨道交通受电弓可靠性分析[J]. 科技創新导报，2016，13（1）：59-61.

[4]卫纬，张红元，张雯，等. 基于故障树分析的塞拉门系统可靠性分析[J]. 机械制造与自动化，2014，43（4）：182-186.

[5]周巧莲，金碧筠，冒玲丽，等. 基于贝叶斯网络地铁车门系统可靠性分析和故障诊断[J]. 沈阳工业大学学报，2014，36（4）：441-445.

[6]何江海，裴卫卫，闫雅斌，等. 基于贝叶斯网络的地铁牵引变电所可靠性分析[J]. 铁路计算机应用，2019，28（8）：68-74.

[7]王佳培，高仕斌，晏紫薇，等. 基于贝叶斯网络的接触网运行可靠性分析[J]. 电气化铁道，2017，28（5）：63-68+74.

[8]王宇，师蔚. 基于故障树-贝叶斯网络的受电弓系统可靠性评估[J]. 测控技术，2017，36（9）：131-134，141.

[9]LIU Zengkai， LIU Yonghong， WU Xinlei， et al. Reliability evaluation of auxiliary feedwater system by mapping GO-FLOW models into Bayesian networks[J]. ISA Transactions，2016， 64：174-183.

[10]古海龙，刘混举. 基于故障树与贝叶斯网络的采煤机故障可靠性分析[J]. 煤炭技术，2015，34（3）：242-244.

[11]李兴运，齐金平. 基于模糊贝叶斯网络的受电弓系统可靠性分析[J]. 铁道科学与工程学报，2018，15（6）：1383-1390.

[12]尹晓伟，钱文学，谢里阳. 系统可靠性的贝叶斯网络评估方法[J]. 航空学报，2008，30（6）：1482-1489.

[13]蒋芹，张轩雄. 基于FTA的贝叶斯网络变送器可靠性评估[J].  电子科技，2018，31（12）：1-4，13.