基于能量损失理论的再生混凝土损伤塑性研究

黄一凡 王向东

摘要 为了研究再生混凝土塑性阶段的损伤演化和刚度劣化，从能量损失的角度基于广义自洽模型对传统的非均质材料能量积分公式进行了重新推导，得到仅含位移的新能量公积分式用以重新定义损伤变量。通过公式计算可以得到损伤过程中的能量变化与劣化后的弹性模量。此外，模拟了再生混凝土单轴压缩，对比了重新定义的损伤变量与传统损伤本构模型的D-x曲线，对比分析发现，重新定义的损伤变量更符合再生混凝土单轴受压的一般破坏规律。

关 键 词 再生混凝土;塑性损伤演化;能量损失;非均质材料能量积分公式;单轴受压

中图分类号 TU528     文献标志码 A

Damage plasticity of recycled concrete based on energy loss theory

HUANG Yifan，WANG Xiangdong

（College of Mechanics and Materials， Hohai University， Nanjing， Jiangsu 211100， China）

Abstract In order to study the damage evolution and stiffness degradation of recycled concrete in the plastic stage， the traditional energy formula of heterogeneous materials is derived based on the generalized self consistent model. And a new energy increment formula with displacement only is obtained to redefine the damage variable. Through the formula calculation， the energy change in the damage process and the elastic modulus after degradation can be obtained. In addition， in order to compare the redefined damage variables with the traditional damage constitutive model， the numerical simulation of recycled concrete under uniaxial compression is carried out， and the damage variables in the process of compression are calculated. It is found that the redefined damage variable is more consistent with the general failure law of recycled concrete under uniaxial compression.

Key words recycled concrete; plastic damage evolution; energy loss; energy integration formula of heterogeneous materials; uniaxial compression

0 引言

再生混凝土作为回收利用废弃混凝土最有效的措施之一，一直以来对再生混凝土（RAC）力学性能的研究多为试验研究。Xiao等[1]对再生混凝土的试验研究进行了综述，发现不同研究者的结论不同甚至相悖。为了使研究更为节省时间、资源、资金，数值模拟已成为研究其力学性能的有效方法并广泛应用[2]。例如，Xiao等[3]对再生混凝土建立了晶格模型并模拟了单轴受压下的应力应变曲线。Zhou等[4]基于随机骨料模型提出了再生混凝土细观力学分析的有限元方法。

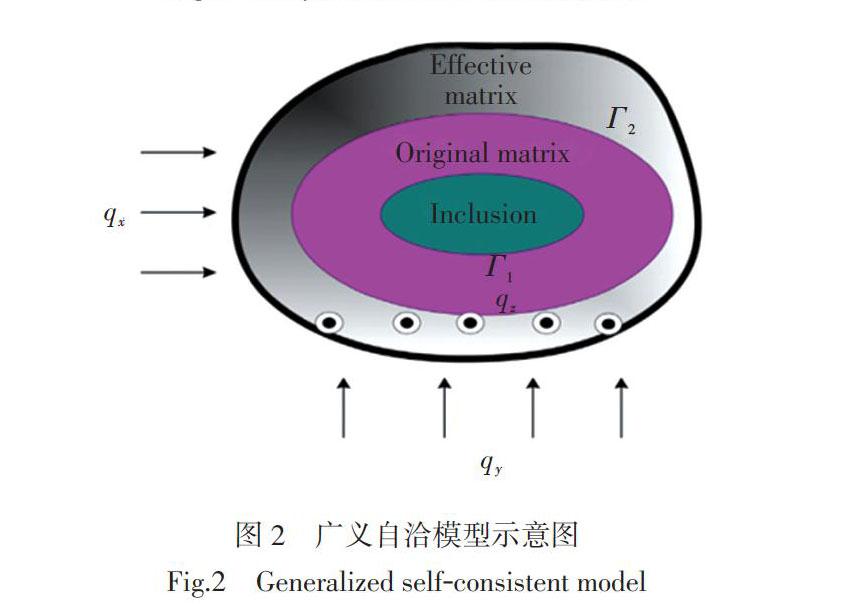
损伤力学主要研究材料内部微观缺陷产生和发展所引起的宏观力学效应及其最终导致材料破坏的过程和规律。从细观来看，与普通混凝土相比，再生混凝土结构更为复杂，一般认为是由天然骨料、旧砂浆、旧界面区、新砂浆、新界面区组成的五相复合材料[5]，如图1所示。国内外学者利用损伤理论提出了针对普通混凝土的损伤模型，例如Loland模型和Mazars模型。对再生混凝土损伤模型的研究忽略了塑性损伤的影响，抑或简化了部分再生混凝土应力应变关系，因而精度受到了一定影响。Xi等[6]提出了混凝土体积模量的广义n相复合模型，如图2所示。该模型假定各组分的泊松比相同，而RAC各相泊松比基本相同[7]，因结构与再生混凝土十分相似可用于推导再生混凝土损伤变量。Peng等[8]通过基于势能原理的基力单元法（BFEM）分析了尺寸对RAC抗拉强度的影响。程卓群[9]基于Najar能量法研究了混凝土动态双轴受压损伤特性。

综上，把再生混凝土当作弹塑性材料，再从能量损失的角度基于广义自洽模型对单轴受压下的再生混凝土损伤变量进行重新定义，数值重构胡晓斌[10]的再生混凝土单轴塑性损伤实验并计算損伤变量进行对比，从而分析再生混凝土的损伤机理。

1 基本公式与推导

将图2中广义自洽模型中Γ1、Γ2定义为RAC中的旧界面与新界面，Inclusion、Original matrix、Effective matrix分别对应RAC的天然骨料、旧砂浆、新砂浆，EI、EM、EE分别为骨料、旧砂浆、新砂浆的弹性模量。qx、qy分别是沿着x、y方向的均匀分布荷载。

基于Dong[11]的工作，对于受远场应力作用的裂纹无限各向同性模型，在模型中源点P处的位移和应力积分方程如下：

[uk（P）=u0k（P）+Γ1Uki（P，q）ti（q）dΓ（q）-Γ1Tki（P，q）ui（q）dΓ（q）+Γ2Tki（P，q）Di（q）dΓ]， （1）

[σkl（P）=σ0kl（P）+Γ1Ukli（P，q）ti（q）dΓ（q）-Γ1Tkli（P，q）ui（q）dΓ（q）+Γ2Tkli（P，q）Di（q）dΓ]， （2）

式中：q是作用在界面上场点;[u0k]和[σ0kl]是由远场均匀分布荷载在p点引起的位移和应力;[Di（q）=ui（q-）-ui（q+）]其中[q-]和[q+]是内部微裂缝上下表面坐标相同的点;[Uki，Tki，Ukli，Tkli]是无限各向同性弹性力学平面问题的基本解[12]

[Uki=18πG（1-ν）（3-4ν）ln（1r）δki+?r?xk?r?xi]， （3a）

[Tki=-14π（1-ν）r?r?n（1-2ν）δki+2?r?xk?r?xi-（1-2ν）?r?xkni-?r?xink]， （3b）

[Ukli=14π（1-ν）r{（1-2v）[δkir，l+δlir，k-δklr，i]+2r，ir，lr，k}]， （3c）

[Tkli=G2π（1-ν）r22?r?n（1-2ν）δklr，i+ν（δkir，l+δlir，k）-4r，ir，lr，k+2ν（nkr，ir，l+nlr，ir，k）+]

[（1-2ν）（2nir，kr，l+nkδli+nlδki）-（1-4ν）niδkl]， （3d）

式中：[δki]是克罗内克算子;[r，i=?r（P，q）?xi（q）]，其中r是源点P与场点q之间的距离;[?r?n=r，ini]，其中ni 是法线在场点q相对于xi的方向余弦;G和ν是剪切模量与泊松比。

当源点P接近位于旧界面区的边界点p，公式（1）变为

[ckiui（P）=u0k（P）+Γ1Uki（P，q）ti（q）dΓ（q）-Γ1cTki（P，q）ui（q）dΓ（q）+Γ2Tki（P，q）Di（q）dΓ]， （4）

式中：[cki]由旧界面区的几何形状决定的常数;符号[∫c]表示柯西主值积分。

当源点P接近位于裂缝表面上的点p，应力积分方程变为

[σkl（p）=σ0kl（p）+Γ1Ukli（p，q）ti（q）dΓ（q）-Γ1Tkli（p，q）ui（q）dΓ（q）+Γ2sTkli（p，q）Di（q）dΓ（q）]， （5）

式中，符号[∫s]表示Hadamard有限部分积分。

由于再生混凝土各相泊松比相同符合广义自洽模型的假定，据Leite[13]的工作，公式（3a）到（3d）可改写为

[UIki=EEIUki]， （6a）

[TIki=Tki]， （6b）

[UIkli=Ukil]， （6c）

[TIkli=EIETkli]。 （6d）

将公式（6a）～（6d）代入公式（4），并考虑边界条件：

[EIUI=EMUM    TI=-TM     uI=uM     tI=-tMfor    q    on     Γ1]， （7a）

[EEUE=EMUM    TM=-TE     uM=uE     tM=-tEfor    q    on     Γ2]。 （7b）

可以得到P在Γ1的位移边界积分方程：

[cki（1+EIE）ui（p）=u0i（p）-Γ1c（1-EIE）Tki（p，q）ui（q）dΓ+Γ2Tki（p，q）Di（q）dΓ]。 （8）

因此，公式（8）可改写为：

[（EIcI（p）+EMcM（p）EE）uM（p）=u0（p）-Γ1（EM-EIEE）TM（p，q）uM（q）dΓ-Γ2（1-EMEE）TE（p，q）uE（q）dΓ]。 （9a）

同理可得P在Γ2的位移邊界方程：

[（cE（p）+EMEEcM（p））=u0（p）-Γ1（EM-EIEE）TM（p，q）uM（q）dΓ-Γ2（1-EMEE）TE（p，q）uE（q）dΓ]， （9b）

式中：[uE（q）]和[TE（P，q）]是场点q在Γ2界面上的位移和牵引力;[uM（q）]和[TM（P，q）]是场点q在Γ1界面上的位移和牵引力。再生混凝土进入塑性阶段产生损伤，同时刚度劣化即弹性模量发生劣化，由此对（9a）及（9b）中的弹性模量求导，结果如下：

[（cE（p）+EMEEcM（p））uE（p）-EME2EcM（p）uE（p）=u0（p）-Γ2（1-EMEE）TM（p，q）uE（q）dΓ-Γ2EME2ETE（p，q）uE（q）dΓ-]

[Γ1（EM-EIEE）TM（p，q）uM（q）dΓ+Γ1（EM-EIE2E）TM（p，q）uM（q）dΓ]， （10a）

和

[（EMcM（p）+EIcI（p）EE）uE（p）-（EMcM（p）+EIcI（p）E2E）uE（p）=u0（p）-Γ2（1-EMEE）TM（p，q）uE（q）dΓ-Γ2EME2ETE（p，q）uE（q）dΓ-]

[Γ1（EM-EIEE）TM（p，q）uM（q）dΓ+Γ1（EM-EIE2E）TM（p，q）uM（q）dΓ]， （10b）

式中，[u=?u?EE]。在数值计算中，对于二维建模的再生混凝土界面区的网格划分一般为Plane82平面8节点单元，因此对公式（10a）及（10b）进行整理，得到如下矩阵方程：

[Hu=u0]， （11a）

[Hu=u0-Hu]， （11b）

式中：[u]和[u0]分别是未知的位移和已知的初始位移;[H]和[H]是（10a）和（10b）的系数矩阵。可由（11a）得到界面区的位移[u]，然后可以用以下公式[14]推导再生混凝土损伤过程中的能量耗散：

[ΔW=W0-Wl=12EE（EM-EI）Γ1t0iuidΓ+（EE-EM）Γ2t0iuidΓ]， （12）

式中，[Wl]为受损状态下的能量。又

[W0=1/2Ωσijε0ijdΩ]。 （13）

线弹性材料的一般本构关系可以用张量表示为下列形式[15]：

[σij=Cijklεkl]， （14）

式中，[Cijkl]是四阶弹性张量，对于各向同性材料可写为：

[Cijkl=λδijδkl+G（δikδjl+δilδjk）]， （15）

式中：[λ=Ev（1+ν）（1-2ν）];[G=E2（1+ν）]。由广义自洽模型假定ν一致可得

[CIijklEI=CMijklEM]。 （16）

将公式（15）代入公式（14）可得

[σIij=EIEMCMijklεkl]。 （17）

则公式（13）可写为

[W0=1/2Ωσijε0ijdΩ=1/2ΩEIEMCMijklεklε0ijdΩ=1/2EIEMΩεklσ0kldΩ=1/2Γt0kukdΩ]。 （18）

将公式（18）代入公式（12），即得到再生混凝土塑性阶段的能量损耗：

[ΔW=1/2I=1N（EM-EI+EEEE）Γ1t0iuidΓ]。 （19）

当[EM=EI]时，即旧砂浆与天然骨料弹性模量一样，则[ΔW=W0]即无损状态，由假设天然骨料不发生损伤，公式成立。

当塑性阶段刚开始，[Wl=0]，即：

[12EE（EM-EI）Γ1t0iuidΓ+（EE-EM）Γ2t0iuidΓ=0]。 （20）

只要给定初始[E0E]，即可通过迭代式（11a）、式（11b）及式（20）即可计算得损伤过程中新砂浆受损后的弹性模量。

Najar损伤理论中将损伤定义为受损状态中与无损状态下的能量比，则据式（18）和（19）可定义损伤变量为

[D=WlW0=W0-ΔWW0=1-I=1N（EM-EIEE）Γ1t0iuidΓΓt0iuidΓ]。 （21）

由公式（19）计算结果可得损伤变量。

2 数值算例

为了验证式（21）计算的损伤变量是否符合再生混凝土受压的一般规律，与胡晓斌[10]试验研究进行对比，文中再生混凝土损伤塑性本构模型如下：

[d=A1xB1                      ，           01，] （22）

式中：[A1]、[B1]、[A2]、[B2]都是由边界条件决定的常数;[C2]、[D2]是由实验数据拟合来的应力应变曲线的参数。

考虑边界条件：

[yx=1=1]，[dydxx=1=0]， （23）

式中，[x=εεc]、[y=σfc]分别为归一化的应变和应力。可以确定[A1]、[B1]、[A2]、[B2]的值：

[A1=1-11-mEsE0，B1=1-mn（1-m）[（（1-m）E0Es）-1]，A2=1-mn（1-m）2EsE0，B2=m（n-1）（1-m）2EsE0]， （24）

式中，[Es]是應力应变曲线峰值的割线斜率。

根据实验数据，拟合曲线可以得到应力应变曲线的参数：

[C2=1.46r2-1.16r+0.71，D2=1.72] 。 （25）

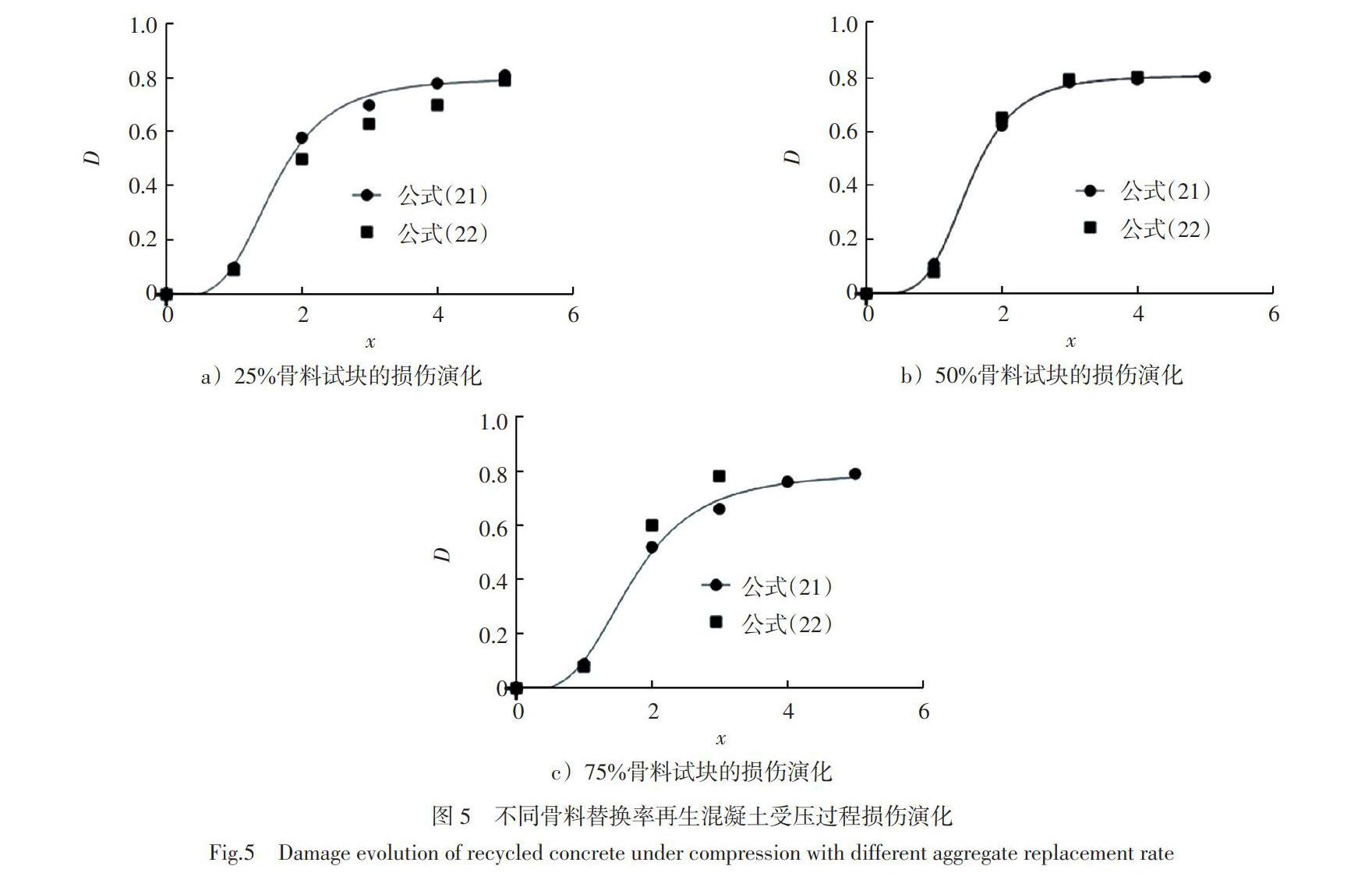
对其实验进行数值模拟重构，细观再生混凝土由天然骨料、旧界面、旧砂浆、新界面新砂浆组成，各相的弹性模量、泊松比和抗拉强度如表1，模拟的试块尺寸为100 mm×100 mm，再生混凝土试块的骨料占比率分别为25%、50%、75%（如图3），并对试块进行单轴加载如图4。

在模拟的过程中，由于再生混凝土抗拉强度比抗压强度低很多，所以忽略了拉伸行为，简化模拟过程。先将模拟的结果代入胡晓斌[10]推导的公式（22）中绘制出点集（22），同时将归一化的[ui=x=εεc]代入公式（21）绘制出点集（21）并与试验[10]拟合的曲线进行对比，如图5。

图5中，由于公式（21）推导的是细观再生骨料的损伤值，而胡晓斌[10]的实验中是宏观再生混凝土试块受压的损伤过程，骨料还没有完全损坏，裂缝已经贯穿再生混凝土失去承载能力，所以损伤值的极限值不是1而是0.8。

本文基于能量损失理论，在广义自洽模型的基础上对非均质材料能量公式进行重新推导，得到了仅含有界面位移的能量公式，由此重新定义了损伤变量，并计算了不同再生骨料替换率的试块单轴受压的损伤演化并与传统损伤模型进行了对比。

1）在0

2）在x>1的区间内，25%骨料替换率的试块，式（22）在塑性阶段损伤演化的较慢，且试块受压断裂后依然没有趋于稳定。而式（21）在位移为4时损伤变量就发展完全趋于稳定。50%骨料替换率的试块，式（21）与式（22）D-x曲线几乎重合。而在75%骨料替换率的试块，式（22）在进入塑性阶段后损伤值迅速上升，再生混凝土试块的力学性能迅速劣化，并于位移为3处就发展完全，式（21）的损伤值继续演化，于位移为5处发展完全并稳定。

3 结论

1）新推导的能量公式只包含位移这一个未知参数，在计算损伤值时比传统损伤本构模型效率更高。

2）隨着骨料替换率的升高，传统损伤本构模型的损伤演化速率升高，预测的再生混凝土试块的寿命缩短。但是再生混凝土试块依然能继续承载，因此低估了再生混凝土的承载力。而较低骨料替换率时，裂缝已经贯穿试块，损伤值依然没有发展完全。由此，新推导的能量公式更能描述再生混凝土受压过程的损伤演化。

参考文献：

[1]    XIAO J Z，LI W G，FAN Y H，et al. An overview of study on recycled aggregate concrete in China （1996-2011）[J]. Construction and Building Materials，2012，31（1）：364-383.

[2]    JAYASURIYA A，ADAMS M P，BANDELT M J. Understanding variability in recycled aggregate concrete mechanical properties through numerical simulation and statistical evaluation[J]. Construction and Building Materials，2018，178：301-312.

[3]    肖建庄，杜江涛，刘琼. 基于格构模型再生混凝土单轴受压数值模拟[J]. 建筑材料学报，2009，12（5）：511-514，518.

[4]    ZHOU H P，PENG Y J，DANG N N，et al. Numerical simulation of uniaxial compression performance for recycled concrete using micromechanics[J]. Applied Mechanics and Materials，2012，253/254/255：550-554.

[5]    肖建庄，刘琼，李文贵，等. 再生混凝土细微观结构和破坏机理研究[J]. 青岛理工大学学报，2009，30（4）：24-30.

[6]    XI Y P，JENNINGS H M. Shrinkage of cement paste and concrete modelled by a multiscale effective homogeneous theory[J]. Materials and Structures，1997，30（6）：329-339.

[7]    MUSIKET K，VERNEREY F，XI Y. Numeral modeling of fracture failure of recycled aggregate concrete beams under high loading rates[J]. International Journal of Fracture，2017，203（1/2）：263-276.

[8]    PENG Y J，PU J W，PENG B，et al. Two-dimensional model of base force element method （BFEM） on complementary energy principle for geometrically nonlinear problems[J]. Finite Elements in Analysis and Design，2013，75：78-84.

[9]    程卓群，彭刚，孙尚鹏，等. 基于Najar能量法的混凝土动态双轴受压损伤特性分析[J]. 水利水运工程学报，2019（4）：100-106.

[10]  HU X B，LU Q W，CHENG S S. Uniaxial damaged plastic constitutive relation of recycled aggregate concrete[J]. Advances in Materials Science and Engineering，2019，2019：1-16.

[11]  DONG C Y，LO S H，CHEUNG Y K. Interaction between coated inclusions and cracks in an infinite isotropic elastic medium[J]. Engineering Analysis With Boundary Elements，2003，27（9）：871-884.

[12]  BREBBIA C A，DOMINGUEZ J. Boundary elements：an introduction course[M]. UK：WIT Press，1994：384-384.

[13]  LEITE L G S，CODA H B，VENTURINI W S. Two-dimensional solids reinforced by thin bars using the boundary element method[J]. Engineering Analysis With Boundary Elements，2003，27（3）：193-201.

[14]  DONG C Y. An interface integral formulation of heat energy calculation of steady state heat conduction in heterogeneous media[J]. International Journal of Heat and Mass Transfer，2015，90：314-322.

[15]  SADD M H. Elasticity：theory，applications，and numerics[M]. Amsterdam：Academic Press，2009：159.