风浪联合作用下半潜式平台运动响应分析
2021-08-09夏恒顾倩段海娟何军
夏恒 顾倩 段海娟 何军

摘要 提出风浪联合作用下深海半潜式生活平台随机运动响应的分析方法。首先,基于50对现场实测风速和波浪数据的相干函数分析,提出深海脉动风速和波浪过程的相干函数模型及其参数估计方法,并由平均样本相干函数估计出模型参数;其次,由脉动风速和波浪的互谱密度矩阵生成深海风速和波浪的随机样本,建立基于风、浪时历输入的SeSam软件分析技术,计算平台的随机运动响应样本;最后,利用移位广义对数分布(Shift Generalized Lognormal Distribution,SGLD)模型和Gumbel Copula,建立平台随机运动响应联合极值分布的估计方法。实际平台的随机风和浪运动响应分析,验证了本文提出方法的有效性。本文的研究对深海半潜式生活平台的安全性和可靠性评估具有一定的参考价值。
关 键 词 深海半潜式生活平台;风浪联合作用;风和浪相干性;SeSam软件;平台运动响应
中图分类号 U674.381 文献标志码 A
Vibration response analysis of deep-sea semi-submersible platforms under the combined excitation of wind and wave
XIA Heng,GU Qian,DUAN Haiguan,HE Jun
(College of Naval Architecture and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract This paper presents an analysis method of the random vibration response of a deep-sea semi-submersible platform under the combined excitation of wind and wave. Firstly, based on the analysis of the coherence function of 50 pairs of field measured wind speed and wave data, the coherence function model of deep-sea fluctuating wind speed and wave process and its parameter estimation method are proposed, and the model parameters are estimated from the average sample coherence function; secondly, the random samples of deep-sea wind speed and wave are generated from the cross spectral density matrix of fluctuating wind speed and wave, establishing the SeSam analysis technology based on wind speed and wave input, calculating platform vibration response. Finally, using the shift generalized lognormal distribution (SGLD) model and Gumbel Copula, the estimation method of joint extreme value distribution of platform random vibration response is established. The effectiveness of the proposed method is verified by the analysis of the random vibration response of an actual deep-sea semi-submersible platform under the combined excitation of wind and wave. The research is of reference value for the safety and reliability evaluation of the deep-sea semi-submersible platform.
Key words deep-sea semi-submersible platforms; combined excitation of wind and wave; coherence of wind and wave; SeSam; platform vibration response
0 引言
在作业和自存工况下,深海半潜式生活平台随时遭受随机风浪联合作用,导致平台在海面上作随机的纵荡、横荡、垂荡、纵摇、横摇和艏摇等6个自由度运动。通常情况下,为了避免动力放大作用,海洋平台(包括深海半潜式生活平台)的基频远低于波浪能量比较集中的频率,然而海风的能量一般都位于低频率内,再加上一些平台(如生活平台)暴露在水面以上的部分比较大,从而导致平台的风致运动比较剧烈。因此,对于诸如深海半潜式生活平台的海上建筑物,需要进行风浪联合作用下的运动响应分析,为平台的安全性和可靠性评估提供支持。
平台随机风和浪運动分析的首要问题是计算风和浪的联合作用。过去40年来,人们先后发展出了共3代波谱模型[1-4],采用数值方法模拟风-浪相互作用和随机风和浪联合过程。波谱模型通常需要大量的计算费用,为此徐亚洲等[5]建立了基本参数为随机变量的Fourier海浪谱,定义风和浪的相互作用,生成随机风和浪载荷。Zaheer和Islam[6]利用风速、有义波高和跨零周期之间的关系,由Pierson-Moskowitz波浪谱,计算风、浪的联合作用,进行铰接塔平台的随机风和浪响应分析。涂志斌[7]提出了随机风场和波浪的同步模拟方法,通过对频率区间和频域区间离散的设置及能量谱矩阵的修正,实现风和浪作用的同步模拟,同步生成海上建筑物风和浪随机响应分析中的风和浪载荷。但考虑风和浪之间相干性即风浪联合作用的研究仍比较薄弱。
深海半潜式生活平台随机风和浪运动分析的第2个关键问题是计算平台运动的样本响应。目前的方法通常是基于风、浪谱或者风浪联合载荷时历,通过使用有限元软件(如SeSam软件、AQWA软件、ANSYS软件、HYDROSTAR等)计算平台的水动力响应[8-11]。其中,SeSam软件是应用比较广泛的软件。采用SeSam软件进行风浪联合作用下半潜式平台的水动力响应分析时,需要解决的技术问题: SeSam中不能输入互谱密度矩阵,从而无法形成考虑风和浪相关性的载荷。
平台随机风和浪运动分析的第3个问题是建立平台非线性随机运动响应极值联合分布的有效估计方法。Jensen和Capul[12]采用FORM(一次可靠度方法)建立了二阶随机波中自升式海洋平台极值响应的估计方法。许超超等[13]采用SGLD(移位广义对数正态分布)和参数估计的两支撑点法建立了随机波浪激励下自升式平台极值响应估计的加速模拟方法。黄孝帝等[14]基于广义极值分布和移位广义对数分布的加速模拟方法有效估计了随机载荷作用下结构的极值分布。何军等[15]建立了预测非线性结构随机地震反应边缘分布的广义高斯分布模型,提出了模型参数化的两点估计方法。
上述几项研究所建立的方法可用于半潜式平台随机风和浪响应的单变量极值估计。而对于随机风浪联合作用下半潜式平台6个自由度运动响应的多变量极值分析,目前还未见相关研究报道。
针对风浪联合作用下深海半潜式生活平台随机运动响应分析中存在的上述问题,本项研究将基于理論建模和深水实测数据建立随机风速和波浪过程的互谱密度矩阵来模拟出考虑风和浪耦合作用的风和海浪时历;开发考虑风和浪相关性的平台运动响应样本的SeSam软件建模和分析技术;提出基于SGLD模型的单变量极值分析和Gumbel Copula函数的多变量极值分析的平台运动极值响应分析方法。从而建立随机风和浪激励下深海半潜式生活平台随机运动响应的有效分析方法。某深海半潜式生活平台的随机风和浪响应分析,将验证所建立方法的效率和数值精度。
1 深海脉动风速和波浪过程的相干函数研究
1.1 基于实测数据的样本相干函数
风、浪耦合机制原理复杂。求脉动风速和波浪过程的相干函数,试验方法具有局限性,无法完全复原海上复杂状况,理论计算如三维数值模拟方法则过于复杂,因此目前主流的研究方法是根据海上实测的数据结合适当的参数化模型,给出合适的相干函数。
本项目的实测数据来自1998年3月12日至4月16日在地中海的里昂湾进行的FETCH试验[16]。实验测量的风速时程为距平均水面高度7 m处的数据,波浪时程和风速时程是同一海上位置处同一时段内的记录,使用Gerling[17]提出的基于多方向谱分析,可将每个谱分为纯风海情况和非纯风海情况海洋波浪的分解方案对测量数据再分析,得到水平风速和浪在纯风海况下的波浪过程记录。风速和波浪记录的时长均为1 710 s,采样频率为12 Hz。
实测数据表明,风速和波浪均近似于平稳的高斯过程。本项目选取50组FETCH实验的风速和波浪测量数据,每组采样长度1 702 s,采样频率为12 Hz。采用9阶向量自回归方法[18]得到脉动风速和波浪过程的自相关函数、互相关函数、自功率谱密度函数和互功率谱密度函数,从而可以得到由实测数据估计的脉动风速和波浪过程的样本相干函数如图1所示。其中细实线为50个样本的各自相干函数(数值解),粗实线为样本平均相干函数。平均样本相干函数为一条单峰曲线,上升到峰值后缓慢下降。
1.2 相干函数的理论模型
为了适用更一般的情况,需要建立风和波浪相干函数的理论模型。由脉动风速与波浪的作用机理可知,距静止水面越高的脉动风与波浪的相干性应越小,平均风速越大,风浪相干性越大;波高越大,风浪相干性越大,波浪的谱峰频率越大,风浪的相干性越小。并结合图1中平均样本相干函数为一条单峰曲线,上升到峰值后缓慢下降,可以假设脉动风速和风浪的相干函数模型具有下述形式:
[yu(z),η(ω)=aω2πczHSTP+u(z)bexp-ω2πczHSTP+u(z)], (1)
式中:[a]为尺度参数;[b],[c]为型参数;[z]为距静止海面的高度;[u(z)]表示高度[z]处的平均风速;[HS]表示波浪的有义波高;[TP=2π/ωP]表示波浪的峰值周期,s。其中常数[a]确保式(1)给出的相干函数的峰值与由实测数据得到的相干函数的峰值一致,常数[b]控制式(1)给出的相干函数的上升段,公式(1)括号内[ω2πczHSTP+u(z)]无量纲,并满足上述风速和波浪的作用机理。[a], [b],[c]确定,通过选择[TP,HS,u(z)]可以得到相应风浪工况下的脉动风速和风浪过程的相干函数。
1.3 模型参数的估计方法
对于式(1)可采用最小二乘法,基于实测相干函数,估计出参数[a]、[b]和[c],从而确定相干函数模型,得到参数的值分别为[a]=0.0125,[b]=4.661,[c]=35.603。图1中粗点划线为采用最小二乘法得到的理论相干函数,从图中可以看出采用最小二乘法得到的理论相干函数峰值远低于平均相干峰,不可取。所以采用另一种方法,利用相干函数模型与平均实测曲线具有相同的峰值频率和峰值这一条件,可得到参数[a]和[c]与参数[b]的关系式:
[a=Δ-bω-bPe-bγmax], (2)
[c=bΔ-1ω-1P], (3)
[Δ=-12πzHSTP+u(z)]。 (4)
式中:[ωP]为实测的相干函数的峰值;[γmax]为实测的相干函数的峰值频率。至此,相干函数模型只有一个独立参数[b],而参数[b]控制式(1)上升段。式中50个样本相干函数的平均值函数称之为“平均相干函数”。b的值是由文中提出的参数估计方法,根据平均相干函数估计得到,取[b]=[5.5],根据式(2)和式(3),可得到[a]≈[4.82×106],[c]=[35.603]。粗虚线是由本文提出的参数估计方法估计的参数代入相干函数理论模型后得到的曲线,在峰值区域较大而在低频与高频处较小。50个样本的平均相干函数峰值为1.490 rad/s,样本波浪谱的平均峰值为1.417 rad/s,可以看出二者非常接近,而根据理论模型与实际峰值频率和峰值相同这一条件得到的理论相干函数放大了风和波浪过程在波浪大部分能量集中区域的相互作用,从结构安全性的角度考虑是可取的。
1.4 风速和波浪样本
由得到的脉动风速过程和波浪过程的相干函数模型,若不考虑风速随高度的变化,海上脉动风速和波浪的互谱密度矩阵为
[S(ω)=Su(z)(ω)Su(z)η(ω)Sηu(z)(ω)Sη(ω)], (5)
式中:[z]代表距平均水面的垂直高度,[u(z,t)]代表[z]处脉动风速过程;[ηt]代表海浪过程;[Su(z)(ω)]和[Sη(ω)]为脉动风速和风浪的双边自谱密度函数;[Su(z)η(ω)]、[Sηu(z)(ω)]为脉动风速[u(z,t)]和波浪[ηt]的互谱密度函数,[Su(z)η(ω)]=[Sηu(z)(ω)]。
由常用的脉动风速谱、波浪谱、脉动风速过程和波浪过程的相干函数模型,容易得到脉动风速[u(z,t)]和波浪[ηt]的互谱密度函数为
[Su(z)η(ω)=Su(z)(ω)Sη(ω)γu(z),η(ω)], (6)
式中,[γu(z),η(ω)]为随机过程[u(z,t)]和[ηt]的相干函数。
为了建立理论的互谱密度矩阵,需要选择合适的脉动风速谱及脉动波浪谱。工程中常用的脉动风速谱一般包括Ochi[19]谱、Davenport[20]谱、Kaimal[21]谱等。其中只有Kaimal谱可以较好拟合样本平均脉动风速谱,其他均无法拟合。如图2脉动风速谱所示,图中细实线为50个样本的脉动风速谱,粗实线为样本平均脉动风速谱,粗虚线为模拟Kaimal谱。常用浪谱有Pierson-Moscowitz谱[22]以及Jonswap谱[23]。其中Jonswap谱比Pierson-Moscowitz谱可以更好拟合平均脉动波浪谱,能量值与样本平均相差很小,而Pierson-Moscowitz谱的能量值比实际平均小很多。图3脉动波浪谱中,细实线为每个样本的实测波浪谱,粗实线为50个样本的平均实测波浪谱,粗虚线为模拟Jonswap谱。
因此,FETCH试验地点的(双边)脉动风速谱和波浪谱分别采用Kaimal谱和JONSWAP谱,可表示为
[Su(ω)=12×2002πu2*zu(z)11+50ωz2πu(z)53], (7)
[Sη(ω)=12×319.34h2sT4pω5exp-1 9481Tpω4γexp-(0.159Tpω-1)22σ2], (8)
式中:[Su(ω)]为脉动风速过程自谱密度函数;[u*]为气流摩阻系数(剪切速度),m/s;z代表距平均水面的垂直高度;[u(z)]为距平均水面高度z处的平均风速。由于取样高度距海面7 m,取50个实测记录平均风速的平均值[u(7)=13.202 m/s],利用平均风剖面的对数律计算出摩擦风速[u*=0.553 m/s]。式(8)中,[Sη(ω)]为波浪过程的自谱密度函数,[γ]为峰升因子,峰升因子介于1.5~6之间,平均值为3.3,[hs]为波浪有义波高,[Tp]为波浪峰值周期,σ为峰形参数。本研究中[hs]=1.860 m,[Tp][=2π/?p] [=2π/1.417] ≈4.434 s,[γ]=3.3,根据Jonswap谱的规定,当[?≤?p] 时σ = 0.07,当[?>?p] 时σ = 0.09。
由所建立的风浪互谱密度矩阵,采用谱分解方法[24],可得到1 000个考虑脉动风速和波浪相干性的风速和波浪随机过程的样本,其中的一个风、浪样本如图4所示。其中图4a)为波浪过程样本,圖4b)为脉动风速过程样本。样本时长3 140 s,步长0.785 s。
2 平台运动响应的样本分析
2.1 SeSam软件及其在平台随机运动样本计算中存在的问题
本项目使用的SeSam软件是研究海洋结构运动响应最常用软件,软件内置常用风谱及波浪谱。但是软件无法直接输入考虑风浪联合作用的互谱密度矩阵得到的风速时历和波浪时历。
2.2 风载荷和波浪载荷的输入
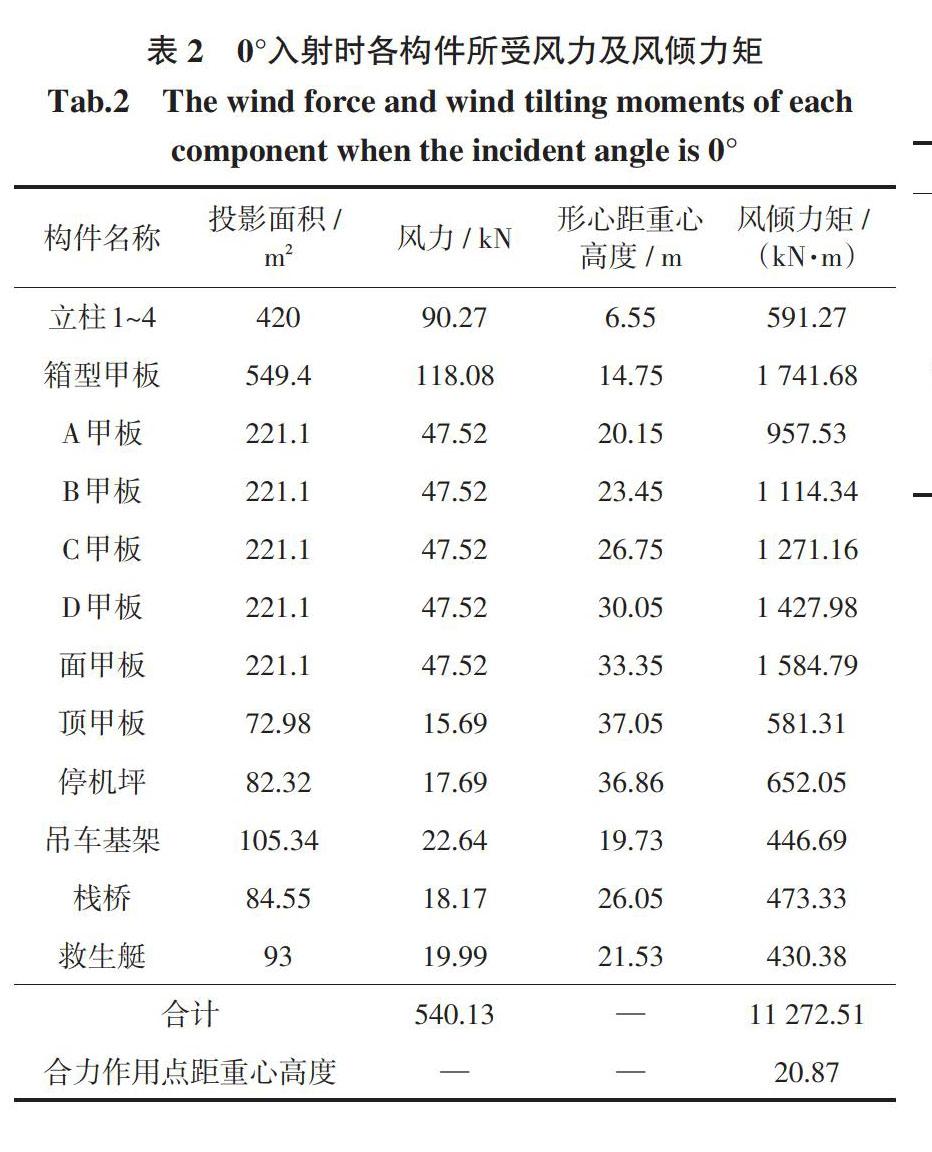
本项目的载荷输入考虑风和波浪的相关性。波浪载荷的输入是在平台湿表面模型、水动力计算及环境参数及系泊系统依次完成后将互谱密度矩阵生成的波浪时历放置在DeepC模块文件根目录。由于软件无法用类似的方法输入风载荷,因此本项目风载荷的输入简化为根据风速极值和平台水面以上部分的面积和分布计算出集中力和力矩作用在平台。然后进行计算,从实际工程安全性角度出发,这么做是合理的。图5为简化的风荷载作用图,将风荷载作用在平台的力分解为作用在重心的集中力及弯矩输入软件中。
2.3 平台运动响应分析的模型
在HydroD模块中由于水下部分尺寸各异,有些无法适用Morison模型,因此本项目统一设定为面元模型,计算的结果更加精确。将GeniE模块中构造的模型导入,根据平台的实际情况设定重心高度,转动半径,垂荡临界阻尼取0.04,以考虑系泊系统对平台的约束。计算可得到该平台的水动力参数。图6为HydroD模块中的平台模型。
本项目在DeepC模块中设定的运动响应时程为2 000 s,步长0.5 s,得到的数据量满足后续极值响应分析要求。参考其他平台系泊缆设计[8],采用枚举法至合理长度,使得运动响应在合理范围内。图7为DeepC模块中的平台模型。
2.4 平台运动响应样本
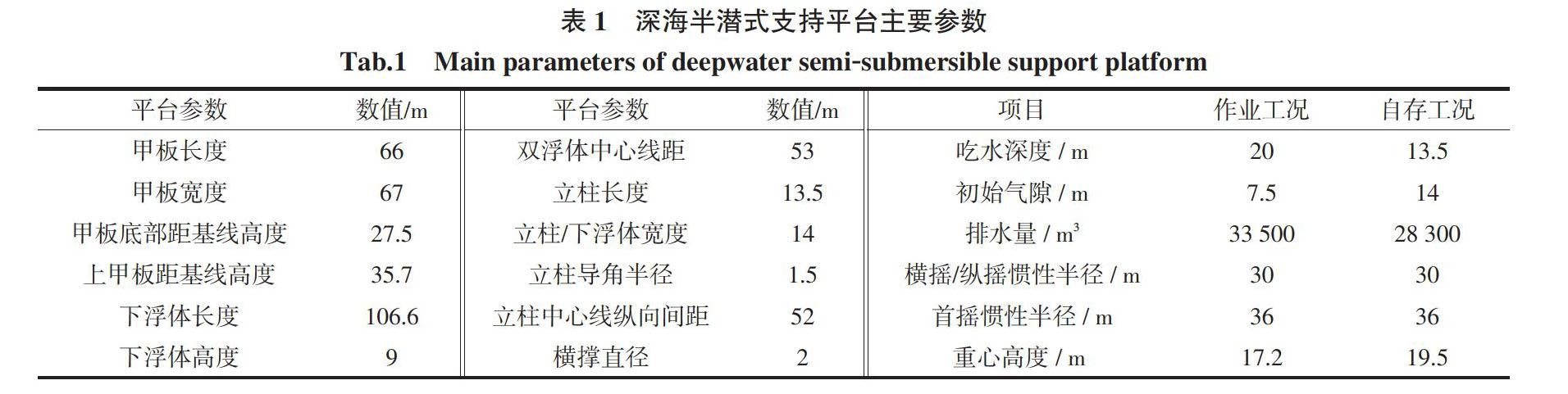
本项目选用我国南海某新型深水半潜式支持平台,作业水深达1 500 m。该平台为我国目前最先进的第六代深海半潜式平台,主体结构由双浮体、双立柱、四横撑以及一个封闭式的甲板所组成。平台各部分的主要参数如表1所示。表2为零度角入射时各构件所受风力及风倾力矩,表3为系泊缆主要参数。采用12点系泊的方式对目标平台进行定位,系泊缆共分为4组,每组3根,分别对称布置于平台四根立柱的外侧。采用锚链-聚酯缆-锚链的三段式组合形式[25],图8为本项目的锚链模型。
由上述SeSam建模和分析技术,设定波浪沿0°入射,得到深海半潜式生活平台风和浪响应的1 000个样本,如图9~图14所示:其中图9到图14分别是第1个样本的纵荡、横荡、垂荡、横摇、纵摇以及艏摇响应,横摇响应和艏摇响应极其微小,可忽略不计。
3 平台随机运动响应的联合极值分布估计
为了进行平台的可靠度和舒适度评估,需要分析深海半潜式生活平台非线性随机风和浪响应的极值分布。另外,考虑各自由度响应之间的相关性,还需要极值响应的联合分布。
3.1 单变量极值响应估计
风和浪激励下平台浮体做6个自由度的运动响应,即纵荡响应、横荡响应、垂荡响应、横摇响应、纵摇响应和艏摇响应。令上述6个自由度的运动响应分别为[ξi(t),i=1,…,6],则其绝对值的极值可以表示为
[Yi=max0≤t≤Tξi(t),i=1,…,6], (9)
式中,T为平台风和浪运动响应的计算持时。
用于单变量极值响应分布估计的模型有指数率模型[26]、广义极值模型(GEV)[27]、广义对数高斯模型(GGS)[28]和移位广义对数模型(SGLD)[29]。本项研究采用广义移位对数正态分布(SGLD)模型,该模型的优势在于可以考虑广阔的偏态-峰度系数空间,可以模拟多种函数类型。其分布函数表达式为
[FY(y)=12+12sgny-bθ-1Q(1r,|lny-bθσ|rr),y>b], (10)
式中:[b]为位置参数;[θ]为尺度参数;[0<σ]和[0 [Q(s,z)=0zts-1e-tdt/Γ(s)]。 由1 000个响应样本,采用矩方法[30],估计的SGLD模型参数值列于表4中。由于横摇响应和艏摇响应极其微小,故忽略不计。 3.2 多变量响应估计 用Gumbel Copula函数来做多变量极值分析的优势在于计算量小,所需样本数量少,传统的Monte Carlo方法做尾部分布估计由于计算量过大,并不可行。 [FY1,…,Y6(y1,…,y6)=P(Y1≤y1,…,Y6≤y6)]为[Y1,…,Y6]的联合分布函数。由Gumbel Copula理论,可得到 [FY1,…,Y6(y1,…,y6)=C(u1,…,u6)=exp{-[(-lnu1)θ+…+(-lnu6)θ]1θ},θ≥1], (11) 式中:[ui=FYi(yi)=P(Yi≤yi),i=1,…,6]为随机变量[Yi,i=1,…,6]的分布函数;[C(u1,…,u6)]为定义域为[0,16]的Copula函数。参数[θ]确定了k-变量随机向量的相依性,[θ=1]表示向量之间是统计独立的,[θ=∞]表示向量之间完全相依。 Copula参数[θ]可由[k≥2]排序的一致性参数Kendall [τ]来计算。整体Kendall [τ]的计算式为 [τ(θ)=126-1-1{-1+26-1Cm1,…,m6(m-1)!(6-1)!(12θ)m-1q=16[Γ(q-1/θ)Γ(1-1/θ)]mq}], (12) 式中,[m=m1+…+m6]由所有的[m1,…,m6]的组合情况计算,整数[m1,…,m6]满足条件[m1+2m2…+6m6=6],而符号 [Cm1,…,m6=6!m1!…m6!1(1!)m1(2!)m2(3!)m3(4!)m4(5!)m5(6!)m6]。 (13) 另一方面,樣本Kendall[τ]的计算式为 [τ=126-1-1[-1+26N(N-1)i≠jI(yi≤yj)]], (14) 式中:[I(·)]为示性函数;[yi≤yj]成立则示性函数的值等于1,否则等于0,其中的[yi]为[Y]的第i个样本,[N]为样本总数。 令由式(12)计算的Kendall[τ]等于由式(14)计算的Kendall[τ],则可求出基于模拟的Copula参数[θ],从而构造出6-变量Gumbel Copula。因此,可以得到平台6个自由度运动响应的多变量极值分布表达式。 本工况环境下,横摇响应和艏摇响应极其微小,可忽略不计。根据1 000个计算样本计算的平台纵荡、横荡、纵摇和垂荡绝对值响应极值的Kendalls tau等于0.104 3,由此数值计算的平台纵荡、横荡、纵摇和垂荡绝对值响应极值的Gumbel Copula参数[θ]=1.127 8。可见平台纵荡、横荡、纵摇和垂荡绝对值响应极值的相依性较小。对于表5列出的设定安全域边界[(x,y,yrot,z)],平台状态为安全的概率[Ps]可由上面构造的4维Gumbel Copula计算出来,计算结果也列于表6中。安全域边界为纵荡、横荡、纵摇和垂荡4个自由度方向的绝对值响应,数值的确定是根据SeSam软件计算得到的响应极值的数值来取各个自由度方向的合理的值,安全域编号由小到大,界限值也逐渐增大。图15为设定的安全域边界及相应的平台处于失效状态的概率,图中由安全域编号5可知,失效的概率仅0.03%,多变量极值响应的尾部估计到10-4,基本满足平台安全性、舒适性和可靠性评估的要求。以纵荡和纵摇绝对值响应的极值为例,其分布尾部绘于图16和图17中。 4 结语 本项研究旨在提出风浪联合作用下深海半潜式生活平台随机运动响应的分析方法。基于实测风速和波浪数据的相干函数分析,提出深海脉动风速和波浪过程的相干函数模型及其参数估计方法,并由样本估计出模型参数;由互谱密度矩阵生成深海风速和波浪的随机样本,建立基于风、浪时历输入的SeSam软件分析技术,计算平台的随机运动响应样本;利用移位广义对数分布(shift generalized lognormal distribution, SGLD)模型和Gumbel Copula,建立平台随机运动响应联合极值分布的估计方法。采用本项研究建立的方法,进行了某深海半潜式生活平台的风和浪响应分析。 本项研究的结论有: 1)本文建立了风浪联合作用下深海半潜式生活平台运动响应分析的有效方法,为深海半潜式生活平台的安全性和可靠性分析,提供技术支撑。 2)本文所建立的方法解决了3个问题。基于理论建模和深水实测数据建立了随机风速和波浪过程的互谱密度矩阵;开发了基于风和浪时历输入的平台运动响应样本的SeSam软件建模和分析技术;提出基于SGLD模型的单变量极值分析和Gumbel Copula函数的多变量极值分析的平台运动极值响应分析方法。 3)实际深海半潜式生活平台的运动响应分析,说明本文所建立方法具有较高的可行性和有效性。 参考文献: [1] EWING J A. A numerical wave prediction method for the North Atlantic Ocean[J]. Deutsche Hydrografische Zeitschrift,1971,24(6):241-261. [2] HOLTHUIJSEN L H, DE BOER S,Wave forecasting for moving and stationary targets, in Computer Modelling in Ocean Engineering[C]// Proceedings of an International Conference on Computer Modelling in Ocean Engineering,Venice,12-23 September 1988:231-234. [3] GROUP T W. The WAM model—A third generation ocean wave prediction model[J]. Journal of Physical Oceanography,1988,18(12):1775-1810. [4] HANSEN J,RUEDY R,GLASCOE J. GISS analysis of surface temperature change. Journal of Geophysical Research,1999,104 (D24):30997-31022. [5] 徐亞洲. 随机海浪谱的物理模型与海洋结构波浪动力可靠度分析[D]. 上海:同济大学,2008. [6] ZAHEER M M,ISLAM N. Dynamic response of articulated towers under correlated wind and waves[J]. Ocean Engineering,2017,132:114-125. [7] 涂志斌. 多维随机荷载组合方法及风浪耦合荷载效应研究[D]. 杭州:浙江大学,2016. [8] 史琪琪. 深水锚泊半潜式钻井平台运动及动力特性研究[D]. 上海:上海交通大学,2011. [9] 朱航,马哲,翟刚军,等. 风浪作用下HYSY-981半潜式平台动力响应的数值模拟[J]. 振动与冲击,2010,29(9):113-118,246. [10] 廖丽恒,周岱,马晋,等. 台风风场研究及其数值模拟[J]. 上海交通大学学报,2014,48(11):1541-1551,1561. [11] 孙雷,罗贤成,姜胜超,等. 适用于渤海海域浮式核电平台水动力特性研究基础与展望[J]. 装备环境工程,2018,15(4):19-27. [12] JENSEN J J,CAPUL J. Extreme response predictions for jack-up units in second order stochastic waves by FORM[J]. Probabilistic Engineering Mechanics,2006,21(4):330-337. [13] 许超超,倪萍,顾颖,等. 随机波浪作用下自升式平台的极值响应估计[J]. 上海交通大学学报,2019,53(12):1404-1410. [14] 黄孝帝,顾颖,何军. 结构极值响应估计方法的有效性研究[J]. 郑州大学学报(工学版),2019,40(1):55-61. [15] 何军,高圣彬. 非线性结构随机地震反应的极值估计[J]. 地震工程与工程振动,2014,34(S1):348-352. [16] DRENNAN W M,GRABER H C,HAUSER D,et al. On the wave age dependence of wind stress over pure wind seas[J]. Journal of Geophysical Research:Oceans,2003,108(C3):8062. [17] GERLING T W. Partitioning sequences and arrays of directional ocean wave spectra into component wave systems[J]. Journal of Atmospheric and Oceanic Technology,1992,9(4):444-458. [18] SIMS C A. Macroeconomics and reality[J]. Econometrica,1980,48(1):1-48. [19] OCHI M K,SHIN V S. Wind turbulent spectra for design consideration of offshore structures[C]// Offshore Technology Conference. Houston,Texas. Offshore Technology Conference,1988. [20] DAVENPORT A G. The spectrum of horizontal gustiness near the ground in high winds[J]. Quarterly Journal of the Royal Meteorological Society,1961,87(372):194-211. [21] SMITH S D,BANKE E G. Variation of the sea surface drag coefficient with wind speed[J]. Quarterly Journal of the Royal Meteorological Society,1975,101(429):665-673. [22] DEODATIS G. Simulation of ergodic multivariate stochastic processes[J]. Journal of Engineering Mechanics,1996,122(8):778-787. [23] 徐德伦,于定勇. 随機波浪理论[M]. 北京:高等教育出版社,2000. [24] MADSEN H O,KRENK S,LIND N C. Methods of structural safety[EB/OL]. 1986 [25] 李建东,陈希,蒋国荣,等. 海洋边界层内风、浪相互作用研究进展[J]. 海洋预报,2005,22(1):58-66. [26] NAESS A,GAIDAI O. Monte Carlo methods for estimating the extreme response of dynamical systems[J]. Journal of Engineering Mechanics,2008,134(8):628-636. [27] GRIGORIU M,SAMORODNITSKY G. Reliability of dynamic systems in random environment by extreme value theory[J]. Probabilistic Engineering Mechanics,2014,38:54-69. [28] JUN H. Approximate method for estimating extreme value responses of nonlinear stochastic dynamic systems[J]. Journal of Engineering Mechanics,2015,141(7):04015009. [29] HE J,GONG J H. Estimate of small first passage probabilities of nonlinear random vibration systems by using tail approximation of extreme distributions[J]. Structural Safety,2016,60:28-36. [30] LOW Y M. A new distribution for fitting four moments and its applications to reliability analysis[J]. Structural Safety,2013,42:12-25.
