建筑数量对土-剪力墙结构建筑群动力相互作用的影响

熊峰 雷鹏 葛琪 吕洋 赵鹏 刘洋 陈江

摘要： 在已完成的土与建筑群动力相互作用振动台试验的基础上，采用有限元方法进行参数分析，研究群效应对结构动力响应的影响。上部结构取为剪力墙，运用ANSYS有限元软件建立了土与建筑群相互作用的有限元模型，模型中运用Davidenkov模拟土体动力非线性。通过调整建筑物数量和布置方式，设置土与3栋建筑、土与5栋建筑、土与7栋建筑三个土?高层剪力墙结构建筑模型，将这三个模型分别与土与单栋建筑的有限元模型进行对比分析。结果表明：当上部建筑群主要沿振动方向布置时，将原剪力墙建筑群中平行于振动方向建筑数量增加后，建筑群群效应会有所增大，并且平行于振动方向的建筑受群效应影响较大;就层间位移对其进行机理分析，结果显示，当受到地震激励时，由于上部建筑的桩基与周围土体两种材料的弹性模量存在着巨大差异，会直接增大上部结构的层间位移，且沿振动方向的周边结构层间位移会大于中央区域结构。

关键词： 土?建筑群動力相互作用; 剪力墙结构; 多种群模型; 数值分析; 机理分析

中图分类号： TU311.3; TU398+.2    文献标志码： A    文章编号： 1004-4523（2021）03-0539-13

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.011

引  言

随着城市建设用地的日益紧张，大量高层建筑群不断涌现。在地震作用下，高层建筑群之间通过场地土的联系形成整体，将产生复杂的土?建筑群动力相互作用（Soil?Structure Cluster Interaction，SSCI）。土?建筑群动力相互作用的群效应是指多栋建筑构成的建筑群在地震作用下发生的与单体建筑不同的反应，它是由地震波在土中传递时在基础间反射形成的。这种群效应除了受土体条件的影响外，与建筑群中建筑的个数、间距以及排列方式等因素都有关。

大多数学者们采用数值分析方法研究土与建筑群的动力相互作用，包括边界元、有限元及边界元与有限元耦合方法[1?2]。?lamo等[3]和Padrón等[4]采用有限元与边界元耦合的方法建立三栋建筑物与土的模型，结果表明，相互作用可以放大或衰减系统响应，与建筑物间距离和整体系统的动态特性有关。李培振等[5]通过ANSYS有限元软件进行了包含两栋建筑的高层建筑土?结构相互作用的研究，得出了考虑群体效应的框剪SSSI体系结构的自振频率与位移峰值均有所减小的结论。近年来，部分学者开始结合振动台缩尺模型来探究土与建筑群的动力相互作用。熊峰等[6]、葛琪等[7?8]、赵丽等[9]设计了两组对比试验，一组为建筑群振动台试验，另一组为单个建筑振动台试验，并建立与之对照的有限元模型进行分析，研究上部结构简化为单自由度体系时，土与建筑群动力相互作用对上部结构动力响应的影响，试验结果显示，在地震作用下，高层建筑群内结构存在明显的相互作用。张昊焓等[10]、牟爽等[11]在此基础上，上部结构采用框架结构，将高层建筑群在地震作用下的动力效应与单独的一栋高层建筑对比，结果表明，群建筑的楼层绝对加速度峰值以及基底剪力峰值都有一定程度的减小，建筑群的群体效应对土体的动力反应也有影响;并且沿振动方向分布的建筑受到的群体效应影响要大于垂直于振动方向的建筑。Aldaikh 等[12]探讨了结构?土?结构相互作用（SSSI）在地震作用下对三栋建筑物群的影响，结果表明建筑群动力相互作用对结构的不利影响比仅有两个相邻结构相互作用的情况更加显著。因此，土与建筑群相互作用的研究对于现实的抗震设计有着重要意义。

虽然目前对土?高层结构建筑群动力相互作用问题的研究逐渐增多，但主要还是集中在对两栋或三栋相邻建筑相互作用的研究，而事实上有文献证明[6?9，12]，密集建筑群的修建可能会导致结构产生更严重的破坏，高层建筑群设计问题上应该考虑土与建筑群间动力相互作用效应[13];同时，大多数研究土体模型采用的是线性模型，在地震激励作用下，土体表现出了强烈的动力非线性特性，在建立土与建筑群动力相互作用模型中，需要考虑土体动力非线性。本文在总结课题组以前研究的基础上，上部结构取为实际尺寸的剪力墙，通过ANSYS建立土与7栋建筑物、土与5栋建筑物和土与3栋建筑物三个土与建筑群有限元模型，并分别与土与1栋建筑物的土与结构有限元模型进行对比分析。在ANSYS软件中通过重启动命令和APDL参数化设计语言，编制程序模拟地震激励作用下土体动力非线性，研究在土?剪力墙建筑群体系中，建筑群间动力相互作用规律，分析高层剪力墙建筑群的地震反应群效应，进一步认识不同类型建筑群效应，为考虑土与建筑群动力相互作用体系的抗震设计提供理论参考。

1 有限元模型简介

1.1 模型介绍

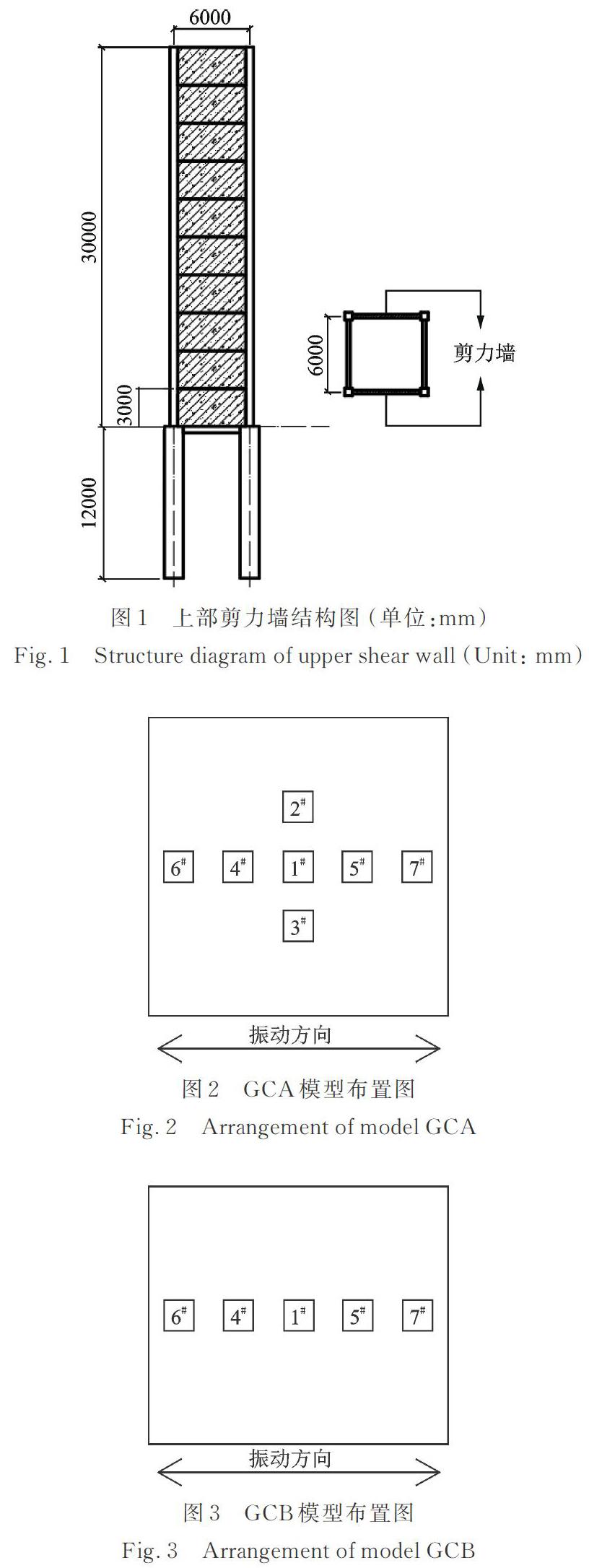
在前期振动台实验及数值模拟基础上，张昊晗等[10]曾通过建立土与框架建筑群的动力相互作用实际模型发现：沿振动方向建筑相比于垂直于振动方向建筑受群效应影响更大，上部建筑不同的布置方位也可能导致不同的结果。基于文献[10]的分析结果，为了进一步分析不同结构和不同布置方式对上部结构动力响应的影响，本文上部结构取剪力墙结构，剪力墙结构图如图1所示，构建土?高层剪力墙结构建筑群模型。设置土与7栋建筑物（GCA）、土与5栋建筑物（GCB）和土与3栋建筑物（GCC）三个土与建筑群有限元模型，结构间距均为6 m，布置方式如图2，3和4所示，并分别与土与1栋建筑物（PCA）的土与结构有限元模型进行对比分析，以进一步探讨土?高层剪力墙结构建筑群动力相互作用的规律。

有限元模型上部结构为10层一跨钢筋混凝土剪力墙结构体系，各层层高3 m，跨度6 m。上部结构楼板厚120 mm;柱子尺寸600 mm×600 mm，梁尺寸为300 mm×500 mm，基础采用柱下独立桩基，截面1500 mm×1500 mm，基础埋置深度12 m;剪力墙厚200 mm，仅沿X方向布置。

上部结构及桩基均采用C35钢筋混凝土，考虑计算成本有限，上部结构在进行有限元计算时不考虑混凝土材料的非线性;同时，钢筋混凝土采用等效弹性模量的方法进行计算，泊松比为0.25，密度为2500 kg/m3。上部结构和土体的自重以节点集中力的方式加入到计算模型中。

1.2 网格划分

有限元模型中，土体范围的选择直接影响到有限元计算的精确程度。土体截取的范围越大，计算越准确，但计算成本较高，计算耗时长，而且对计算机要求较高;土体截取范围越小，计算成本越低，但准确性难以得到保障。同时，在地震作用下边界的存在会使计算域内的波无法透过边界向外逸散，这也将影响计算的精度。根据前人的研究成果，取30倍结构宽度的横向边界进行计算，基本可以消除边界的影响[5]。

在构建有限元模型时，网格的划分是一个关键环节，网格划分的形式将对计算精度和计算成本产生直接影响。本文在进行网格划分时考虑以下原则：

波动对网格划分的影响。如果单元尺寸过大，则波动的高频部分难以通过。对于一般的沿竖向传递的剪切波，单元高度可根据以下公式取值

式中  为剪切波速，fmax为截取的最大波动频率。单元的平面尺寸比高度尺寸的要求稍低，一般取hmax的3?5倍。

综合考虑计算成本及精度需求，本文各模型中土体采用三维实体单元Solid185，上部结构楼板采用壳单元Shell181。Shell181单元参数选取情况为：keyopt（1）=0，keyopt（3）=0，keyopt（8）=0，keyopt（9）=0，keyopt（10）=0，柱子、梁和基础均采用梁单元beam188，beam188单元参数选取情况为：keyopt（1）=1，keyopt（4）=2，剪力墙采用Shell63单元。土体截取范围为600 m×600 m，深度20 m，分三层。土体底部固定，四周为自由边界。按上述网格划分原则，单栋建筑PCA模型共含有单元4853 12个，7栋建筑GCA模型共含有单元492224个，5栋建筑GCB模型共含有单元489920个，3栋建筑GCC模型共含有单元487616个。有限元模型网格划分如图5所示。

1.3 地基土参数

本文有限元模型加入了土体动力非线性模型，采用Davidenkov等效线性模型模拟地震过程中土体的动力非线性特征。该土体动力非线性模型在课题组前期的振动台试验中已经得到证明[6?9]，振动台试验结果与振动台试验的有限元模型结果吻合得较好，证明了该模型模拟土体动力非线性的准确性，以下是Davidenkov模型的详细介绍和在ANSYS中的试验过程。

1.3.1 地基土本构模型

土的非线性本构模型是土?结构相互作用数值模拟计算中的关键，本文将土体视为黏弹性介质，采用Davidenkov等效线性模型，关系如下式所示

式中  为动剪切模量比;为动剪应变;A，B和为与土性有关的拟合参数;为土的质量密度，为土的剪切波速。阻尼比公式采用陈国兴等[14]提出的考虑初始阻尼比的經验公式，如下式

式中  Dmin，D0和β为拟合参数。

1.3.2 土体参数

选取三种类型的土体，从底部到顶部高度分别为5，5和10 m。建筑场地为Ⅱ类场地，各层土体的材料参数如表1所示。各层土体在Davidenkov模型里面对应的土的动剪切模量比G/Gmax和阻尼比D随剪应变的变化关系，取自于袁晓铭等所做土体试验[15]，对国内10余个不同地区的土进行了共振柱自振试验，试验土包括黏土、粉质黏土、粉土、沙土、淤泥和淤泥质土，得到了各类土的动剪切模量比G/Gmax和阻尼比D随动剪应变γ的变化曲线，提取曲线中的数据，如表2所示。

根据表2的数据可以得到Davidenkov模型的相应参数。

1.3.3 土动力非线性实现过程

利用ANSYS的参数设计语言将土拟合曲线中的数据并入计算程序中，根据土的动剪切模量G和阻尼比D与动剪应变γ之间的关系，通过迭代使G，D与γ相协调，以近似求解土的非线性动力反应。本文利用ANSYS有限元软件的重启动分析方法来模拟上述过程，进行土体分析时，先代入初始动剪切模量G1和初始阻尼比D1，通过ANSYS软件计算出每个土单元相应的剪应变，根据剪应变计算出相应的每个土单元的动剪切模量G2和阻尼比D2，再采用修改了的动剪切模量G2和阻尼比D2进行重启动分析。以此类推，即用动剪切模型Gi和阻尼比Di进行计算，得出下一组动剪切模量Gi+1和阻尼比Di+1，当前后相邻两组Gi，Di和Gi+1，Di+1的差值在允许范围内时，中止计算。

1.4 输入地震波

本文通过ANSYS节点约束命令在模型底部所有节点输入地震波加速度时程，输入地震波以水平振动方式（即X方向）在模型中传播。分析采用EL?Centrol波和唐山波（后文中均简称EL波与TS波），考虑到计算成本，两条波都截取包含加速度峰值在内的10 s持时，同时对地震波加速度峰值进行调幅，调为2.2 m/s2，以模拟7度罕遇地震。

2 结果分析

2.1 建筑群动力相互作用影响系数

为了便于比较建筑群模型与单个结构模型地震反应的差异，定义群效应影响系数如下

式中  e称为群效应影响系数，S0为地震波激励下单个结构模型的结构地震反应（楼层绝对加速度、层间位移、基地剪力）峰值，对应为考虑土与单个结构相互作用的PCA模型中单栋建筑的地震反应;S为地震波激励下建筑群模型的结构地震反应（楼层绝对加速度、层间位移、基地剪力）峰值，对应为考虑SSCI效应的GCA，GCB和GCC模型的结构地震反应。作为评价单个结构模型和建筑群模型中的结构地震反应差异大小的指标，当影响系数e为正值时，表明考虑SSCI效应时，结构的动力反应会减小;当影响系数e为负值时，表明结构动力反应会增大。

2.2 结构反应分析

2.2.1 GCA模型

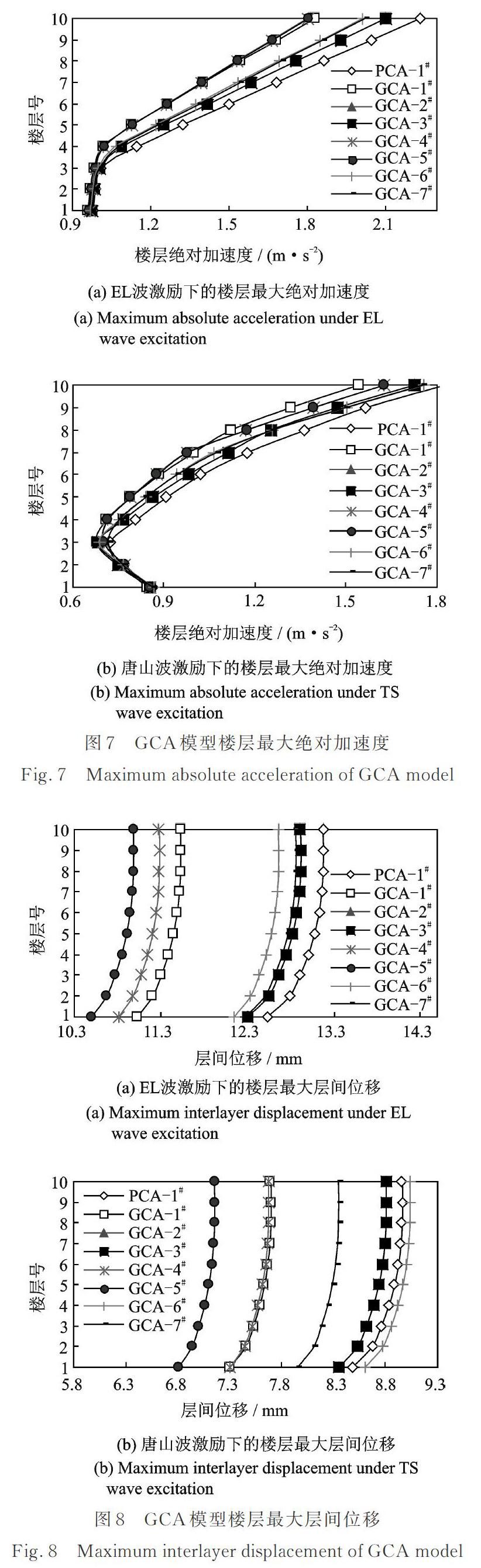
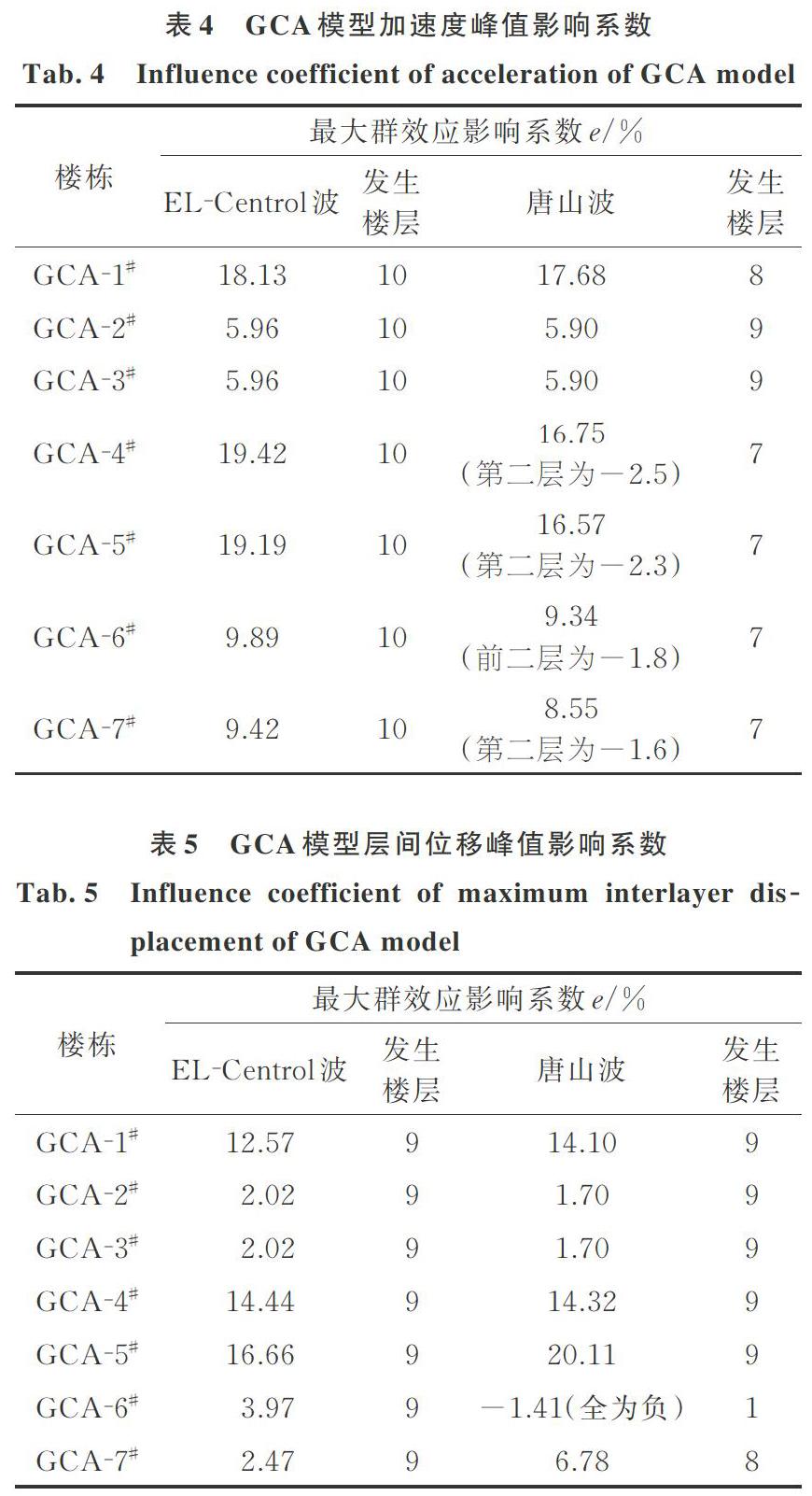
图6，7和8分别给出了土?高层建筑群相互作用体系（GCA模型）和土?单栋上部结构相互作用体系（PCA模型）在EL波和唐山波激励下的基底剪力峰值、楼层绝对加速度峰值和层间位移;表3，4和5分别为其对应的群效应影响系数。

可以发现，在两种地震波激励下，对于基底剪力峰值，GCA模型中各建筑的地震反应均小于PCA模型中的单栋建筑。对于楼层绝对加速度，在EL?Centrol波激励下，GCA模型中各建筑的地震反应均小于PCA模型中的单栋建筑，其规律与基地剪力峰值相似。但在唐山波激励下，GCA模型中平行于振动方向建筑GCA?4#，GCA?5#，GCA?6#和GCA?7#，第二层的绝对加速度峰值群效应影响系数均为负，其中建筑GCA?4#第二层群效应影响系数最大为-2.5%，表明其地震反应超过了PCA模型中的单栋建筑。

对于层间位移，从图8中可以看出，在EL?Centrol波激励下，GCA模型中各建筑的层间位移均小于PCA模型中的单栋建筑。其中平行于振动方向中间区域的三栋建筑GCA?1#，GCA?4#和GCA?5#的群效应影响系数都较大，表明此三栋建筑受群效应影响较大，层间位移峰值相比于PCA模型中的单栋建筑下降较多;平行于振动方向端部两栋建筑GCA?6#，GCA?7#的层间位移峰值下降较小;垂直于振动方向的两栋建筑GCA?2#，GCA?3#的群效应影响系数最小，其层间位移地震反应与PCA模型中的单栋建筑相近。相比于PCA模型中的单栋建筑，平行于振动方向建筑的最大层间位移都减小，但端部建筑的层间位移明显大于中间三栋建筑。在唐山波激励下，GCA模型内部建筑的层间位移地震反应规律与EL?Centrol波激勵下的模型出现了差异，平行于振动方向端部建筑GCA?6#的各楼层层间位移群效应影响系数都为负，其层间位移地震反应高于PCA模型中的单栋建筑PCA?1#。

由此可知，SSCI效应对建筑物地震反应的影响与输入的地震波有关。土与建筑群动力相互作用体系中，周边的结构动力响应大于中央结构的动力响应。

2.2.2 GCB模型

图9，10和11分别给出了土?高层建筑群相互作用体系（GCB模型）和土?单栋上部结构相互作用体系（PCA模型）在EL波和唐山波激励下的基底剪力峰值、楼层绝对加速度峰值和层间位移;表6，7和8分别为其对应的群效应影响系数。

可以发现，在两种地震波激励下，对于基底剪力峰值和楼层绝对加速度峰值，GCB模型中各建筑的地震反应均小于PCA模型中的单栋建筑。中间区域建筑GCB?1#，GCB?4#和GCB?5#各项指标的群效应影响系数较为相近，其值都较大，表明其地震反应相比于PCA模型中的单栋建筑都减小很多;端部建筑GCB?6#，GCB?7#的各项指标的群效应影响系数较小，其地震反应大于平行于振动方向中间三栋建筑，小于PCA模型中的单栋建筑。在EL波激励下，5栋建筑的GCB模型的楼层层间位移峰值相比于PCA模型中的单栋建筑PCA?1#都减小，在唐山波激励下，最左侧建筑GCB?6#的楼层层间位移群效应影响系数均为负，绝对值最大达到了0.51%，其地震反应略高于PCA模型中的单栋建筑PCA?1#，而其余四栋建筑都不同程度减小。与GCA模型相似，GCB模型端部建筑的层间位移明显大于中间三栋建筑。

2.2.3 GCC模型

图12，13和14分别给出了土?高层建筑群相互作用体系（GCC模型）和土?单栋上部结构相互作用体系（PCA模型）在EL波和唐山波激励下的基底剪力峰值、楼层绝对加速度峰值和层间位移;表9，10和11分别为其对应的群效应影响系数。

可以发现，在两种地震波激励下，对于基底剪力峰值、楼层绝对加速度峰值这两个地震反应指标，GCC模型中各建筑的地震反应均小于PCA模型中的单栋建筑。对于GCC模型，无论是施加EL波还是唐山波的激励，内部三栋建筑的楼层层间位移峰值群效应影响系数均为负，其地震反应都高于PCA模型中的单栋建筑PCA?1#。其中，群内建筑GCC?1#的楼层层间位移地震反应最大，在EL波、唐山波激励下的最大群效应影响系数分别为-5.59%，-6.36%。

由以上GCA，GCB和GCC模型的分析可知，在GCA，GCB模型中，相比只考虑土与单个结构相互作用效应的单栋建筑，群效应会使群内建筑的基底剪力峰值减小;对于楼层绝对加速度，除部分建筑个别楼层有所增大外，其余也均减小;对于层间位移，除唐山波作用下的6#建筑外，其余建筑层间位移峰值也均有所减小。在GCC模型中，建筑群中建筑仅布置于沿垂直于振动方向，此时群效应也会使群内建筑的基底剪力峰值、楼层绝对加速度峰值都减小，群内建筑的楼层层间位移相比于只考虑土与单个结构相互作用效应的单栋建筑会增大，且中间建筑增加较多。

3 机理分析

3.1 模型及地震波分析

对PCA，GCA，GCB和GCC四个模型分别进行模态分析后，得到各自前10阶固有频率如表12所示。

其中GCA模型第8阶开始出现上部结构沿X方向交替平动，GCB模型第6阶开始出现上部结构沿X方向交替平动，GCC模型第4阶开始出现上部结构沿X方向交替平动，振型图如图15所示。PCA模型前两阶振型为上部结构沿X，Y方向的平动，考虑SSCI效应之后，建筑群的模态发生了变化，导致建筑群模型内结构间动力响应出现变化，如第二节有限元计算结果分析，沿着振动方向的周边建筑的层间位移大于中间结构。

提取唐山波和EL?Centrol波的傅里叶幅值谱如图16所示。其中EL?Centrol波相对较大的两个傅里叶幅值对应频率分别为1.172，1.465 Hz，唐山波对应的分别为1.172，1.563 Hz。可以发现GCC模型上部结构开始沿X方向平动的频率（1.586 Hz）与EL?Centrol波和唐山波傅里叶幅值谱中第二峰值对应频率非常接近，这将加大GCC模型的动力响应，故GCC模型中的基底剪力峰值影响系数与加速度峰值影响系数普遍小于GCA和GCB模型对应值，甚至GCC模型的层间位移峰值影响系数更是均为负数。同时，唐山波第二个较大的傅里叶幅值对应的频率1.563 Hz更加接近于GCC模型中上部结构沿X方向的频率1.586 Hz，所以导致在GCA和GCB模型中，在唐山波地震作用下，平行于振动方向端部建筑的层间位移大于单体结构模型PCA的层间位移，而在EL?Centrol波作用下，除了GCA和GCB模型中6#结构外，其余上部结构的层间位移均小于PCA模型上部结构的层间位移。

3.2 桩土相互作用

在以上模型中，地震波均施加于模型底部所有节点，模型受地震波激励时，由下层节点带动上层节点进行运动，如图17所示。

底部节点受沿X负方向的加速度地震波激励后，在0?8 m高度范围内，水平方向上由于只存在单一材料土体，故此高度范围内的模型发生一致变形。考虑底层节点最先受到地震波激励，上层节点由于惯性会保持原有静止状态不变，故0?8 m高度范围内的土体受地震波激励后，0 m处与8 m处会产生水平位移差，其变形如图18所示。

在8?12 m高度范围内，同一水平面上不僅存在土体，还存在钢筋混凝土桩。根据前文模型参数，钢筋混凝土桩截面直径1500 mm，桩深12 m，其刚度远远大于土体。对于8?12 m高度范围内的土体，当底部节点受沿X负方向的加速度地震波激励后，位于8 m的节点最先开始沿X负向运动。在下层节点带动上层节点向X负向运动的过程中，由于惯性会使上下节点间产生位移差，并且，由于桩土之间巨大的刚度差异，两种材料的位移差也存在着巨大差异。如图19所示，M为在8 m处的桩与土体的位移，两者一致，A为位于20 m处土体顶部的位移，B为位于20 m处桩顶部的位移，M-A为土体顶部底部的位移差，M-B为桩顶部底部的位移差。由于桩的刚度远远大于土体，故位移B大于位移A，桩的上下位移差小于土体的上下位移差，也即是桩的变形小于土体的变形。

由于桩土之间的变形差，模型在向X负向振动时，土会对桩身产生侧压力，如图20所示。在侧压力的作用下，桩的侧向变形会增加，最终桩土达到变形协调，新的位置如虚线所示。从整体模型来看，如图21所示，以建筑GC?6#，GC?4#为例，可以发现建筑GC?6#左侧土体范围远远大于建筑GC?4#左侧土体范围，也即表明在向X负向运动的过程中，建筑GC?6#的桩身所受的侧压力远大于建筑GC?4#的桩身所受侧压力，所以建筑GC?6#的桩侧向变形会大于建筑GC?4#的桩侧向变形，也即建筑GC?6#的基础转动将大于建筑GC?4#，这也将导致建筑GC?6#的层间位移大于建筑GC?4#。同理，当模型沿X正向振动时，也可以得出另一端的建筑GC?7#的层间位移将大于中间区域的建筑。

根据前文多个模型的计算结果，对于包含7个建筑的GCA模型以及包含5个建筑的GCB模型，可以发现，建筑群中端部建筑的层间位移峰值均大于中间区域建筑，符合此规律。

4 结  论

本文通对高层剪力墙结构进行分析，调整上部建筑数量及布置方式，扩大下部土体边界范围，构建出土与7栋建筑物、土与5栋建筑物和土与3栋建筑物三个土与建筑群有限元模型，并分别与土与1栋建筑物的土与结构有限元模型进行对比分析。通过有限元计算分析，得出如下主要结论：

1）相比于只考虑土与单个结构相互作用效应的单栋建筑：对于基底剪力，群效应会使群内建筑的地震反应都减小;对于楼层绝对加速度，除部分建筑个别楼层有所增大外，其余也均减小;对于层间位移，除唐山波激励下沿振动方向端部建筑的地震反应增大以外，其余也均减小，并且都是沿振动方向周边结构层间位移峰值大于中央区域结构;对于以控制位移为抗震设计目标的高层建筑来说，应该加以考虑。

2）当上部建筑群主要沿振动方向布置时（GCA、GCB模型），将原剪力墙建筑群中平行于振动方向建筑数量增加后，建筑群群效应会有所增大，并且平行于振动方向建筑受群效应影响较大。

3）当上部建筑群的布置方式仅存在垂直于振动方向的布置时（GCC模型），相比于只考虑土与单个结构相互作用效应的单栋建筑，高层剪力墙结构建筑群群效应会使群内建筑的基底剪力峰值、楼层加速度峰值这两个地震响应指标都不同程度的下降;同时群效应会使群内所有建筑的层间位移均增加，并且中间建筑增加较多。这是由于此种布置方式的模型沿X方向平动的频率与地震波的主频率相近，加大了模型的动力响应所致。

4）对其中桩土作用进行分析，可知当受到地震激励时，上部建筑的桩基与周围土体都将因惯性而产生变形，并且由于桩土两种材料的弹性模量存在着巨大差异，两者产生的变形程度也将不同，由于这种非一致变形，土体对桩产生侧压力，将导致基础发生转动，会直接增大上部结构的层间位移。同时，位于端部建筑周围土体区域较大，在受到振动时，土体对桩产生的侧压力也高于中间区域建筑，这也将导致端部建筑的层间位移高于中间建筑。而中间区域建筑底部周围土体范围较小，受地震波激励因惯性产生非一致变形而产生的侧压力也较小，基础转动也较小，导致中间区域建筑的层间位移较小。最终在建筑群中会出现沿振动方向周边结构层间位移大于中央区域结构。

参考文献：

[1] Clouteau D， Aubry D. Modification of ground motion in dense urban areas[J]. Journal of Computational Acoustics， 2001， 6： 1659?1675.

[2] Nateghi-A F， Rezaei-Tabrizi A. Nonlinear dynamic response of tall buildings considering structure?soil?structure effects[J]. The Structral Design of Tall and Special Buildings， 2013，22（14）：1075-1082.

[3] ?lamo G M， Padrón L A， Aznárez J J， et al. Structure-soil-structure interaction effects on the dynamic response of piled structures under obliquely incident seismic shear waves[J]. Soil Dynamics and Earthquake Engineering， 2015， 78： 142-153.

[4] Padrón L A， Aznárez J J， Maeso O. Dynamic structure?soil?structure interaction between nearby piled buildings under seismic excitation by BEM?FEM model[J]. Soil Dynamics and Earthquake Engineering， 2009， 29： 1084-1096.

[5] 李培振，严克非，徐鹏. 地震下考虑群体效应的高层建筑土-结构相互作用研究[J]. 土木工程学报，2014，47（S1）：1-5.

LI Peizhen， YAN Kefei， XU Peng. Study on dynamic interaction between soil and group of high-rise buildings under seismic excitation?[J]. China Civil Engineering Journal， 2014， 47（S1）： 1-5.

[6] 熊峰，赵丽，谢伦武，等.考虑土-高层建筑群动力相互作用的振动台试验研究[J]. 四川大学学报（工程科学版），2015，47（3）：37-43.

XIONG Feng，ZHAO Li，XIE Lunwu，et al. Shaking table test of high-rise building group-soil interaction[J]. Journal of Sichuan University （Engineering Science Edition）， 2015，47（3）：37-43.

[7] 葛琪，熊峰，陈  江，等. 软土地基上土?高层建筑群体系对高层建筑影响的试验研究[J]，振动与冲击，2016，35（12）：102-109.

GE Qi，XIONG Feng，CHENG Jiang，et al. Tests of effect of soil-high-rise Buildings built on soft soil foundation on high-rise building[J]. Journal of Vibration and Shock，2016，35（12）：102-109.

[8] 葛琪.考虑场地效应的土-高层建筑群动力相互作用振动台试验与有限元分析[D].成都：四川大学，2013.

GE Qi. Shaking table test and finite element analysis of soil and high-rise building group dynamic interaction considing the site effect[D]. Chengdu： Sichuan University， 2013.

[9] 赵丽，熊峰，葛琪，等. 土-高层建筑群相互作用对场地土影响的试验研究[J]. 地震工程与工程振动，2014， 34（6）：90-96.

ZHAO Li，XIONG Feng，GE Qi，et al. Test study on effects of soil-high-rise buildings interaction on site soil [J]. Journal of Earthquake Engineering and Engineering Vibration， 2014， 34（6）：90-96.

[10] 張昊焓，熊峰，葛琪.土-框架建筑群动力相互作用有限元模拟分析[J].地震工程与工程震动，2017，37（5）：169-177.

ZHANG Haohan， XIONG Feng， GE Qi. Finite element simulation of solid-framed building cluster dynamic interaction[J]. Journal of Earthquake Engineering and Engineering Vibration，2017，37（5）：169-177.

[11] 牟爽，葛琪，熊峰，等.土与高层建筑群相互作用的群体效应分析[J].四川建筑科学研究，2018，44（6）：27-33.

MOU Shuang， GE Qi， XIONG Feng， et al. Analysis of cluster effect of interaction between soil and high-rise buildings[J]. Sichuan Building Science，2018，44（6）：27-33.

[12] Aldaikh Hesham， Alexander Nicholas，Ibraim Erdin， et al. Two dimensional numerical and experimental models for the study of structure-soil-structure interaction involving three buildings[J]. Computers and Structures， 2015， 150： 79-91.

[13] Trombetta N W， Mason H B， Chen Z， et al. Nonlinear dynamic foundation and frame structure response observed in geotechnical centrifuge experiments[J]. Soil Dynamics and Earthquake Engineering， 2013， 50： 117-133.

[14] 陈国兴，刘雪珠. 南京及邻近地区新近沉积土的动剪切模量和阻尼比的试验研究[J]. 岩石力学与工程学报，2004，23（8）：1403-1410.

CHENG Guoxing，LIU Xuezhu.Test study on ratio of dynamic shear moduli and ratio of damping for recently deposited soils in Nanjing and its neighboring areas[J].Chinese Journal of Rock Mechanics and Engineering， 2004，23（8）：1403-1410.

[15] 袁晓铭，孙锐，孙静，等. 常规土类动剪切模量比和阻尼比试验研究[J]. 地震工程与工程振动，2000，20（4）：133-139.

YUAN Xiao-ming， SUN Rui， SUN Jing， et al. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils?[J]. Journal of Earthquake Engineering and Engineering Vibration，2000，20（4）：133-139.

作者简介： 熊  峰（1963-），女，博士，教授，博士生导师。E-mail： fxiong@scu.edu.cn

通讯作者： 葛  琪（1984-），女，博士，副教授。E-mail： geqi@scu.edu.cn