面向机器人笛卡尔空间的轨迹运动自适应抑振控制

李琳 古智超 张铁

摘要： 工业机器人的柔性传动部件导致机器人末端产生振动，严重降低笛卡尔运动精度，为此提出自适应输入整形抑振控制策略。以“双惯量模型+PD控制”建立关节伺服系统模型，分析振动特性。由于运动中的振动信号存在较大噪声，无法准确辨识振动频率和阻尼比，故采用基于递推最小二乘法（Recursive Least Squares， RLS）的任意时延输入整形器自适应设计方法。通过对笛卡尔轨迹规划的归一化插补函数输入整形，提出笛卡尔轨迹输入整形方法，实际表现为重新规划笛卡尔速度大小而不改变运动方向。输入整形抑振实验中直线轨迹振动信号能量最大降低77.08%，圆弧轨迹振动信号能量最大降低31.07%，残余振动信号能量降低80%以上，验证了所述抑振控制策略能有效抑制机器人笛卡尔运动启停时的振动。

关键词： 工业机器人; 振动抑制; 柔性关节; 自适应输入整形; 笛卡尔运动

中图分类号： TP242.2; TB535    文献标志码： A    文章编号： 1004-4523（2021）03-0499-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.007

引 言

工业机器人的柔性传动部件（如谐波减速器、同步带等）启动和停止时导致机器人末端存在较大的振动，严重降低了运动精度[1]。在工业生产中，要求工业机器人具备高速、高精度的运动控制特点，故需要研究抑制末端振动的控制策略。柔性关节通常采用双惯量模型描述，振动现象属于伺服系统的机械谐振[2]。常用的伺服振动控制方法包括陷波滤波器[3?4]、状态反馈法[5?6]、迭代学习控制[7] 、输入整形器[8?9]等。

输入整形器利用特定的脉冲序列与参考输入进行卷积运算得到抑振控制输入。与陷波滤波器和低通滤波器相比，输入整形器的抑振效果更优且具有更短的滤波时间长度[10]。在相同的抑振评价标准下，与三角形速度、梯形速度等平滑化指令相比，输入整形器具有更短的轨迹时长和更强的鲁棒性[11]。典型的输入整形器设计方法为利用振动信号辨识系统的振动频率和阻尼比后计算脉冲幅值和作用时间，对于振动信号噪声较大的系统，因难以准确辨识频率和阻尼比而大大增加了设计难度，基于递推最小二乘法的自适应设计方法则能很好地解决该问题[12?13]。

针对工业机器人振动问题，国内外学者提出了不少输入整形方法。李琳等[14]针对工业机器人固定时长点到点运动的残余振动问题，提出采用误差补偿的关节轨迹输入整形方法。Kim等[15]在工业机器人上分别应用最优S型轨迹、鲁棒ZV整形器和动态ZV整形器设计预整形轨迹，有效抑制圆弧运动的残余振动，但是存在轮廓误差问题。Zhao等[16]设计零时延输入整形器对笛卡尔轨迹整形，减少了滞后时间和机器人的运动超调量。Aribowo等[17]建立并辨识工业机器人液体搬运任务的振动模型，设计ZV整形器对直线运动的加速度整形，有效抑制液体在运动过程中和停止后的振动。

6自由度机器人的笛卡尔运动由关节运动耦合产生，直接对笛卡尔运动的关节轨迹整形，会产生轮廓误差。一方面考虑到运动过程的振动信号噪声问题较严重，准确辨识模态参数的难度大;另一方面振动控制必须避免轮廓误差问题。针对工业机器人笛卡尔空间中典型的直线和圆弧运动，本文基于递推最小二乘法设计任意时延输入整形器，采用笛卡尔轨迹规划与输入整形相结合的方法，实现自适应抑振控制。

1 工业机器人末端振动现象

1.1 柔性关节伺服系统

目前大部分商用工业机器人采用各关节独立PID控制方式，将柔性传动部件等效为扭转弹簧，电机轴和关节负载等效为两个惯量进行建模，忽略阻尼的柔性关节传动系统如图1所示，采用PD控制的关节伺服系统框图如图2所示。

图2中，为电机角度和关节角度输入;为电机角度和关节角度输出;为电机惯量和关节惯量;K为柔性减速器的刚度;n（n>1）为减速比;KP，KD为比例系数和微分系数。关节角度闭环传递函数G（s）如下式所示

为获得较快的响应速度、较小的稳态误差和合适的附加阻尼，KP和KD通常设定得较大（如本文使用的机器人关节1的KP=1，KD=20），使得关节角度在频率处存在谐振峰值，本文主要讨论采用输入整形方法抑制由此产生的机器人末端振动。

1.2 机器人末端振动控制

采用线性插补函数规划匀速直线轨迹，机器人末端速度为346.41 mm/s，运动时间为1000 ms，使用三向加速度传感器实时测量末端不同方向的加速度，振动信号如图3所示。从图3可知，在启停时机器人末端因速度突变而存在振动现象。

2 输入整形器自适应设计方法

2.1 基于递推最小二乘法的整形器设计

本文采用文献[12]提出的任意时延输入整形器，其传递函数如下式所示

式中 A为脉冲幅值，Td为脉冲作用时间间隔，M为脉冲个数。对于存在N阶振动频率的柔性系统，任意时延输入整形器的脉冲个数M应满足。为抑制关节伺服系统在反共振频率处的振动，取输入整形器的脉冲个数M=3。假设系统是线性的，则可将整形滤波环节后移，利用振动信号y（t）设计输入整形器，自适应设计流程如图4所示。

经预实验测试得到离散振动信号y（n），可由下式計算对应时刻n输入整形滤波输出yf（n）

以零振动为约束条件，即目标输出yfd（n）=0，估计误差为yfd（n）-yf（n）。选择递推最小二乘法为自适应算法，迭代方程如下所示：

2.2 任意时延整形器设计分析

RLS方法存在“数据饱和”问题，随着迭代次数增加，和的元素将趋于0，对脉冲幅值的修正作用减弱。为增加新输入数据的权重，引入遗忘因子对式（5），（6）修正后如下式所示

时与2.1节RLS方法一致。在实际应用中，遗忘因子取值范围通常为0.9?1，取值过小会加剧噪声干扰。下式为二阶系统的自由振动响应

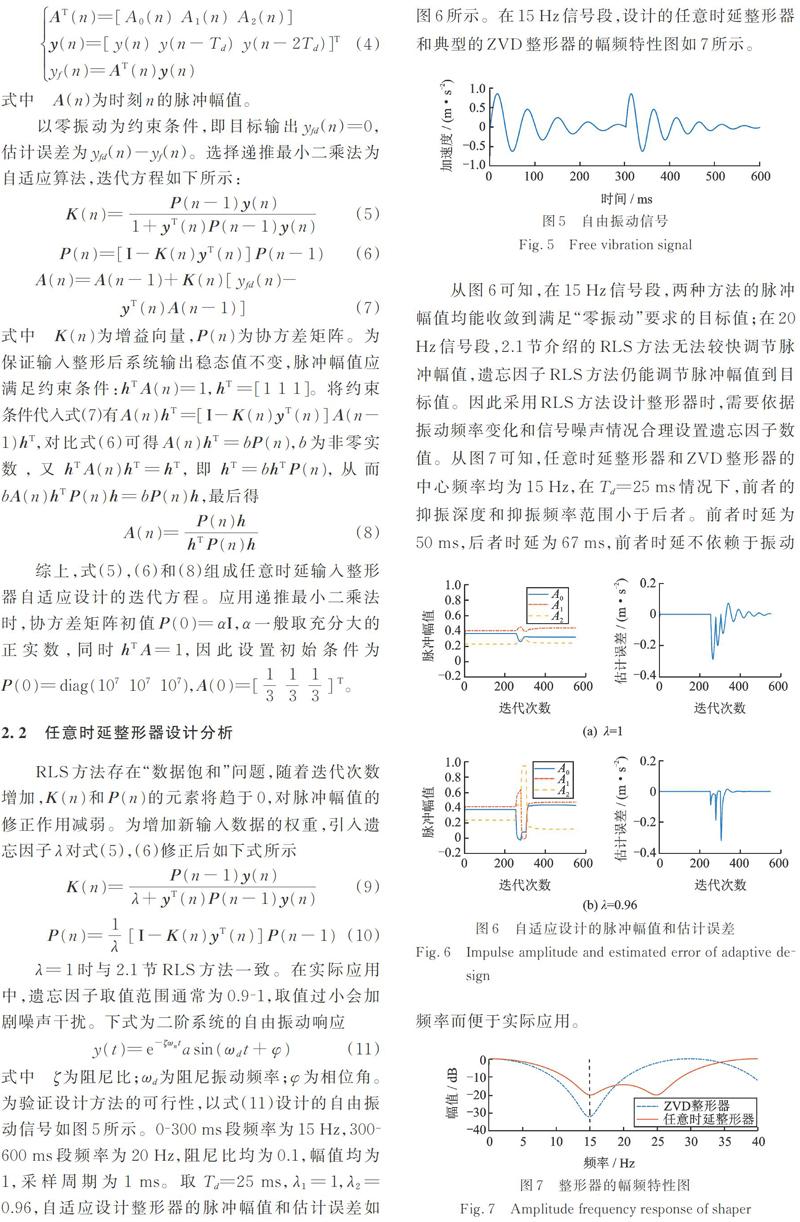
式中 ζ为阻尼比;ωd为阻尼振动频率;φ为相位角。为验证设计方法的可行性，以式（11）设计的自由振动信号如图5所示。0?300 ms段频率为15 Hz，300?600 ms段频率为20 Hz，阻尼比均为0.1，幅值均为1，采样周期为1 ms。取Td=25 ms，自适应设计整形器的脉冲幅值和估计误差如图6所示。在15 Hz信号段，设计的任意时延整形器和典型的ZVD整形器的幅频特性图如7所示。

从图6可知，在15 Hz信号段，两种方法的脉冲幅值均能收敛到满足“零振动”要求的目标值;在20 Hz信号段，2.1节介绍的RLS方法无法较快调节脉冲幅值，遗忘因子RLS方法仍能调节脉冲幅值到目标值。因此采用RLS方法设计整形器时，需要依据振动频率变化和信号噪声情况合理设置遗忘因子数值。从图7可知，任意时延整形器和ZVD整形器的中心频率均为15 Hz，在Td=25 ms情况下，前者的抑振深度和抑振频率范围小于后者。前者时延为50 ms，后者时延为67 ms，前者时延不依赖于振动频率而便于实际应用。

3 笛卡尔轨迹输入整形方法

3.1 笛卡尔轨迹规划

工业机器人笛卡尔轨迹规划包括直线规划和圆弧规划，包含笛卡尔坐标插补和逆运动学计算等步骤[18]。直线规划的插补方法如下式所示

式中 D0为起始位姿点，D1为结束位姿点，D（t）=[x（t） y（t） z（t） α（t） β（t） γ（t）]T，（x，y，z）为位置坐标， （α，β，γ）为姿态角，f（t）为归一化插补函数，f（0）=0，f（T）=1，插补区间为[0，T]。圆弧规划以圆弧所在平面建立坐标系O2?UVW如图8所示，为O2?UVW到基准坐标系O1?XYZ的齐次变换矩阵。利用f（t）对圆心角插补得到，圆弧位置坐标插补如下式所示

式中 为对应坐标的插补变化量。利用机器人逆运动学求解位姿点对应的关节角度，得到驱动机器人的关节轨迹。

3.2 笛卡尔空间输入整形

工业机器人笛卡尔速度和关节速度的映射关系由雅克比矩阵描述，如下式所示

式中 为雅克比矩阵。当雅克比矩阵可逆时，有关系式

利用输入整形器对笛卡尔速度进行线性滤波，能对关节速度产生滤波效果。因为笛卡尔速度由插补函数决定，故提出笛卡尔轨迹输入整形方法如下：

Step1：选择归一化函数f（t）进行笛卡尔轨迹规划，驱动工业机器人运动，测量机器人末端的加速度作为振动信号y（n）;

Step2：根据采集的振动信号自适应设计任意时延输入整形器;

Step3：对f（t）整形得线性滤波的归一化插补函数fIS（t），重新进行笛卡尔轨迹规划得到整形轨迹。

上述提出的笛卡尔轨迹输入整形方法仅对f（t）整形，实际表现为对笛卡尔速度大小进行重新规划，不改变运动方向，从而避免了轮廓误差的产生。

4 实验及结果分析

4.1 自适应设计整形器实验

基于6自由度工业机器人搭建实验平台，机器人的D?H参数如表1所示。采用KISTLER公司三向加速度传感器测量末端振动信号，测量范围为±30g，模拟量由倍福模块采集。控制平台为研华510工控机，采用EtherCAT总线通讯，控制同步周期为1 ms，实验平台如图9所示。

采用抛物线过渡的线性函数设计直线和圆弧轨迹，加、减速段时间占插补时间比例为0.05。直线轨迹起点和终点分别为D0=[229.2 -32.5 537.7 -0.362 0.067 -2.779] T，D1=[429.2 167.5 337.7 -0.362 0.067 -2.779] T，运动时间为1000 ms;圆弧轨迹的三个位姿点分别为DA=[-416.3 322.0 166.7 -0.664 -1.471 -0.220] T，DB=[127.5 423.6 238.6 -1.186 -1.497 -1.159] T，DC=[402.7 329.2 210.1 -1.186 -1.497 -1.770] T，运动时间为2000 ms，笛卡尔轨迹如图10所示。

因加速度信号存在衰减的情况，以振动幅值较大、振动较明显的加速度方向为参考振动方向，截取0?550 ms加速度信号进行零均值化得到离散振动信号，离散傅里叶变换（Discrete Fourier Transform， DFT）后得到频谱图，直线和圆弧轨迹的振动信号和频谱图如图11所示。考虑到振动信号仅存在单个峰值频率且圆弧轨迹的振动信号噪声较大，取遗忘因子λ=1。设定脉冲作用时间间隔Td=25 ms，自适应设计整形器的脉冲幅值、估计误差和幅频特性图如图12所示，输入整形器参数如表2所示。

从图12可知，脉冲幅值收敛较快，估计误差在迭代200次后能收敛在±0.5 m/s2内，说明基于递推最小二乘法的自适应方法在振动信号存在一定噪声时仍可满足实际应用要求。在抑振鲁棒性方面，以-14 dB为目标抑振深度，直线轨迹的整形器中心频率为13.94 Hz，抑振频率范围为11.72?17.02 Hz;圆弧轨迹的整形器中心频率为13.6 Hz，抑振频率范围为12.64?14.66 Hz。两组振动信号的DFT峰值频率为14.5 Hz，说明设计的输入整形器能有效减弱输入信号的共振成分且具有一定鲁棒性，满足各关节振动频率不完全相同的应用场景。

4.2 轮廓误差分析

为定量研究轮廓误差，直线轮廓误差定义为直线插补点到名义直线轨迹的垂直距离;圆弧轮廓误差定义为圆弧插补点到圆心的距离与名义圆弧半径之差。对插补函数整形后进行笛卡尔轨迹规划，圆弧轨迹的插补位置、插补速度和插补加速度如图13所示，轮廓误差对比如图14所示。

關节轨迹整形中直线和圆弧的最大轮廓误差分别为0.1312 mm和0.0388 mm。笛卡尔轨迹整形仅对插补函数整形，理论上不产生轮廓误差，实际中出现的小偏差是基于雅克比矩阵的逆运动学计算造成的。综上，直接对笛卡尔运动的关节轨迹整形会引入轮廓误差，而笛卡尔轨迹整形则避免轮廓误差问题。

4.3 抑振效果分析

笛卡尔轨迹整形的直线轨迹和圆弧轨迹抑振效果对比分别如图15和16所示，笛卡尔整形轨迹在启动和停止时振动幅值远小于未整形轨迹。采用下式计算振动信号能量

以运动中的振动信号计算过程振动信号能量，以停止后500 ms振动信号计算残余振动信号能量，结果如表3所示。

在直线运动中，与未整形滤波比较，笛卡尔轨迹整形的加速度传感器X，Y，Z轴振动信号能量分别降低58.37%，42.81%，77.08%，残余振动信号能量分别降低98.15%，98.55%，80.60%。在圆弧运动中，与未整形滤波比较，笛卡尔轨迹整形的加速度传感器X，Y，Z轴振动信号能量分别降低31.07%，10.78%，29.70%，残余振动信号能量分别降低98.45%，95.25%，99.39%。抑振实验验证本文提出的笛卡尔轨迹输入整形方法能有效抑制工业机器人笛卡尔运动启动和停止时的末端振动，从而提高笛卡尔运动的稳定性。

5 结 论

本文针对6自由度工业机器人笛卡尔运动的振动问题，提出基于递推最小二乘法设计任意时延输入整形器的抑振控制策略，实验结果验证方法的可行性和有效性，得到结论如下：

（1）在振动信号存在较大噪声时，准确辨识振动频率和阻尼比难度较大，基于递推最小二乘法设计的输入整形器能有效减弱输入信号的共振成分且具有一定鲁棒性，能满足应用需求。

（2）对笛卡尔轨迹规划的插补函数进行输入整形，表现为重新规划笛卡尔速度大小而不改变运动方向，解决了直接对笛卡尔运动的关节轨迹输入整形的轮廓误差问题;笛卡尔轨迹输入整形的直线振动信号能量最大降低达77.08%，圆弧振动信号能量最大降低达31.07%，残余振动信号降低80%以上，表明所述方法能有效抑制工业机器人笛卡尔运动启停时的振动。

参考文献：

[1] Dwivedy S K. Dynamic analysis of flexible manipulators， a literature review[J]. Mechanism and Machine Theory， 2006， 41（7）：749-777.

[2] Ghorbel F， Hung J Y， Spong M W. Adaptive control of flexible joint manipulators[C]. Proceedings，1989 International Conference on Robotics and Automation， Scottsdale， AZ， USA，1989：1188-1193.

[3] Wiersma R D， Wen Z， Sadinski M， et al. Robust position servo system based on vibration suppression control for industrial robotics[C]. The 2010 International Power Electronics Conference-ECCE ASIA，Sapporo， Japan，2010：2230-2237.

[4] Chen Y， Yang M， Long J， et al. Analysis of oscillation frequency deviation in elastic coupling digital drive system and robust notch filter strategy[J]. IEEE Transactions on Industrial Electronics， 2018，66（1）：90-101.

[5] Takesue N， Furusho J， Fujinaga K. Control using joint torque sensor of robot arm with two‐inertia resonance： Comparison with control using state‐estimation observer[J]. Electrical Engineering in Japan， 2006， 156（2）：75-84.

[6] Spong M W. On the force control problem for flexible joint manipulators[J]. IEEE Transactions on Automatic Control， 1989， 34（1）：107-111.

[7] Lange F， Hirzinger G. Learning accurate path control of industrial robots with joint elasticity[C]. Proceedings 1999 IEEE International Conference on Robotics and Automation， Detroit， MI， USA， 1999：2084-2089.

[8] Singhose W. Command shaping for flexible systems： A review of the first 50 years[J]. International Journal of Precision Engineering and Manufacturing， 2009， 10（4）：153-168.

[9] Hekman K， Singhose W， Lawrence J. Input shaping with Coulomb friction compensation on a solder cell machine[C]. Proceedings of the 2004 American Control Conference， Boston， USA，2004：728-733.

[10] Singhose W， Vaughan J. Reducing vibration by digital filtering and input shaping[J]. IEEE Transactions on Control Systems Technology， 2011， 19（6）：1410-1420.

[11] Singhose W， Eloundou R， Lawrence J. Command generation for flexible systems by input shaping and command smoothing[J]. Journal of Guidance， Control， and Dynamics， 2010， 33（6）：1697-1707.

[12] Rhim S， Book W J. Adaptive time-delay command shaping filter for flexible manipulator control[J]. IEEE/ASME Transactions on Mechatronics， 2004， 9（4）：619-626.

[13] Chu Z Y， Hu J. An improved recursive least square?based adaptive input shaping for zero residual vibration control of flexible system[J]. Advances in Mechanical Engineering， 2016， 8（4）：1-14.

[14] 李  琳， 胡锡钦， 邹焱飚， 等. 采用误差补偿输入整形技术的振动控制[J].振动工程学报，2019，32（6）：996-1002.

Li Lin，Hu Xiqin，Zou Yanbiao，et al. Reducing vibration by error compensation input shaping technique[J]. Journal of Vibration Engineering， 2019，32（6）：996-1002.

[15] Kim J， Croft E A. Preshaping input trajectories of industrial robots for vibration suppression[J]. Robotics and Computer Integrated Manufacturing， 2018， 54：35-44.

[16] Zhao Y， Chen W， Tang T， et al. Zero time delay input shaping for smooth settling of industrial robots[C].2016 IEEE International Conference on Automation Science   and Engineering （CASE）， Fort Worth， TX， USA，2016：620-625.

[17] Aribowo W， Yamashita T， Terashima K， et al. Input shaping control to suppress sloshing on liquid container transfer using multi-joint robot arm[C]. 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems， 2010：3489-3494.

[18] 陈伟华.工业机器人笛卡尔空间轨迹规划的研究[D].广州：华南理工大学，2010.

作者简介： 李 琳（1962?），女，博士，教授。电话： （020）87114635; E-mail：linli@scut.edu.cn

通讯作者： 张  铁（1968?），男，博士，教授，博士生导师。电话：13660733192;E-mail：merobot@scut.edu.cn