基于FLAC3D的压裂工况下地应力重新分布规律研究*
2021-08-09张瑞萍窦益华杨晓儒李明飞
张瑞萍 祝 云 窦益华 杨晓儒 李明飞
(1西安石油大学机械工程学院 2新疆油田分公司勘探事业部)
0 引 言
压裂液的注入将导致储层地应力的重新分布,引起套管外载荷和受力状态的改变,进而影响套管的强度安全性。目前针对地应力对压裂的影响研究较多,对压裂后的地应力重新分布规律的研究较少。因此有必要深入考察压裂后储层地应力分布特征,提高压裂工况下地应力的预测精度,为套管强度安全性分析提供载荷依据。
针对压裂工况下地应力重新分布规律的研究,很多文献给出了相关的研究方法和技巧。于浩等[1]建立了地层-水泥环-套管二维有限元模型,对压裂过程应力场重新分布规律进行了有限元分析。郑永香等[2]基于断裂力学理论,建立了地应力转向模型和地应力差值的计算方法,分析了单裂缝周围的地应力场分布及其影响因素,但只研究了裂缝周围地应力的变化。吴寒和王振宇等[3-4]建立了油藏三维应力场模型,明确了储层的岩石力学特性和地应力分布状态,但未考虑射孔参数。B.R.MEYER等[5-7]针对应力阴影范围的计算,通过有限元软件对地应力重新分布规律进行了研究。龚小卫等[8]对压裂过程中裂缝延伸对地应力的影响进行模拟研究和分析,研究了人工裂缝延伸过程中对地应力的影响。尚宝兵等[9]以岩石力学研究为基础,研究了井斜角和方位角变化对储层破裂压力的影响。孟召平等[10]揭示了研究区储层水力压裂裂缝分布特征。郭恩昌等[11]根据热弹性力学和渗流力学理论,探讨了压裂工况下压力场和温度场对地应力场的影响。刘雨等[12]推导出压裂过程中地层应力分布计算模型,得出水平井压裂时存在诱导应力使地应力状态发生改变。董光等[13]建立了初始地应力作用下的计算模型,研究重复压裂前井眼和裂缝附近地应力并通过计算得出了应力场和孔隙压力随空间和时间的变化特征。郭建春等[14]建立了地层应力场分布数学模型,研究了人工裂缝周围水平应力场的分布情况。张广明等[15]建立了页岩气藏水平井体积压裂数值模型,研究了压裂过程中地层应力场的分布及其变化。
综上所述,部分研究采用有限元分析以及相似材料模拟试验,但建立的三维模型不够完整,未考虑射孔参数,也有部分研究分析了压裂参数对裂缝的影响,但没有具体分析地应力重新分布的问题。本文为了获得压裂工况下地应力的重新分布规律,以四川某油田井下5 000 m压裂过程为研究对象,应用FLAC3D软件建立射孔后储层-水泥环-套管模型,分析了储层初始应力以及压裂工况下地应力的重新分布规律。采用的研究方法可提高压裂工况下地应力的预测精度,同时可为套管强度安全性分析提供载荷依据。
1 地应力叠加原理
压裂工况下,地应力场主要由初始地应力场、井筒周围的诱导应力场以及压裂裂缝诱导应力场耦合而成。其中,超过3 倍井眼直径以外范围井筒周围的诱导应力场变化不大。因此,压裂工况下地应力场分布主要由初始地应力场和压裂裂缝诱导应力场组成。初始地应力场主要由上覆岩体自重和水平方向构造应力叠加得到。
1.1 上覆岩体自重产生的地应力分析
上覆岩体自重产生的地应力为:
(1)
(2)
(3)

若考虑孔隙压力p,则其产生的应力为:
(4)
(5)
(6)
式中:φ为有效应力系数。
1.2 水平方向构造应力分析
水平方向构造应力为地壳运动引起的应力分量,是地应力场非均匀性的主要原因。水平方向构造应力的计算公式为:
(7)
(8)

1.3 总初始地应力场分析
地应力可表示为3个方向的主应力,即垂直应力σz、最大水平主应力σm和最小水平主应力σn:
σz=σv
(9)
(10)
(11)
由式(1)~式(11)可得,当泊松比越大时,x与y方向的水平地应力也越大,二者几乎都呈线性增长关系。在参数确定的情况下,一定深度储层初始地应力场只与储层深度有关,且随着储层深度的增加,储层初始地应力场z方向应力值增大。
2 地应力场重新分布模型建立
2.1 几何模型建立
在以往的研究中,通常将模型看成平面应变问题,建立二维仿真模拟图,即只考虑与套管轴线垂直平面的应变,但实际上三维模型更能反映出地应力的变化情况。为了更准确地研究地应力场的初始平衡以及压裂工况下储层地应力场重新分布规律,本文以四川某油田井下5 000 m压裂过程为研究对象,建立了射孔后储层-水泥环-套管模型。模型中套管外径为 139.7 mm,壁厚为9.17 mm,钢级为 P110,井眼直径为 215.9 mm。根据圣维南原理,储层模型边界到井眼的距离取井眼直径的5~7倍,则边长取2 000 mm。建模关键参数如表1所示。
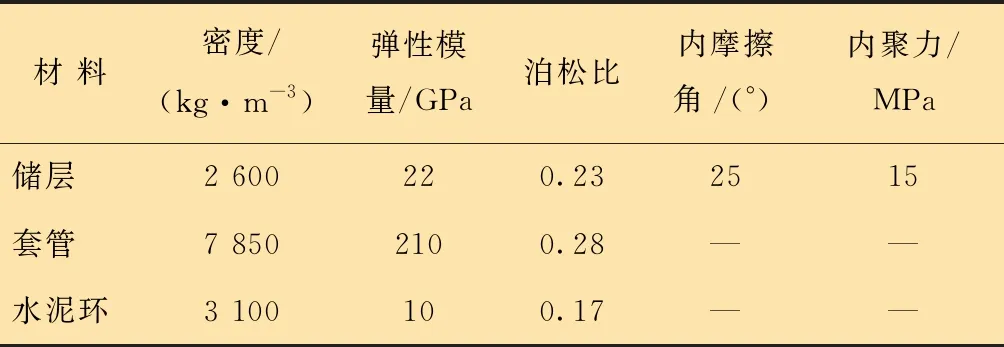
表1 建模关键参数Table 1 Key modeling parameters
建立一段2.0 m×2.0 m×1.2 m的储层-水泥环-套管三维模型,其中井眼在此模型的正中心部分,取长度1.0 m、射孔孔密16孔/m、相位角90°、轴向间距62.5 mm,射孔后模型如图1所示。
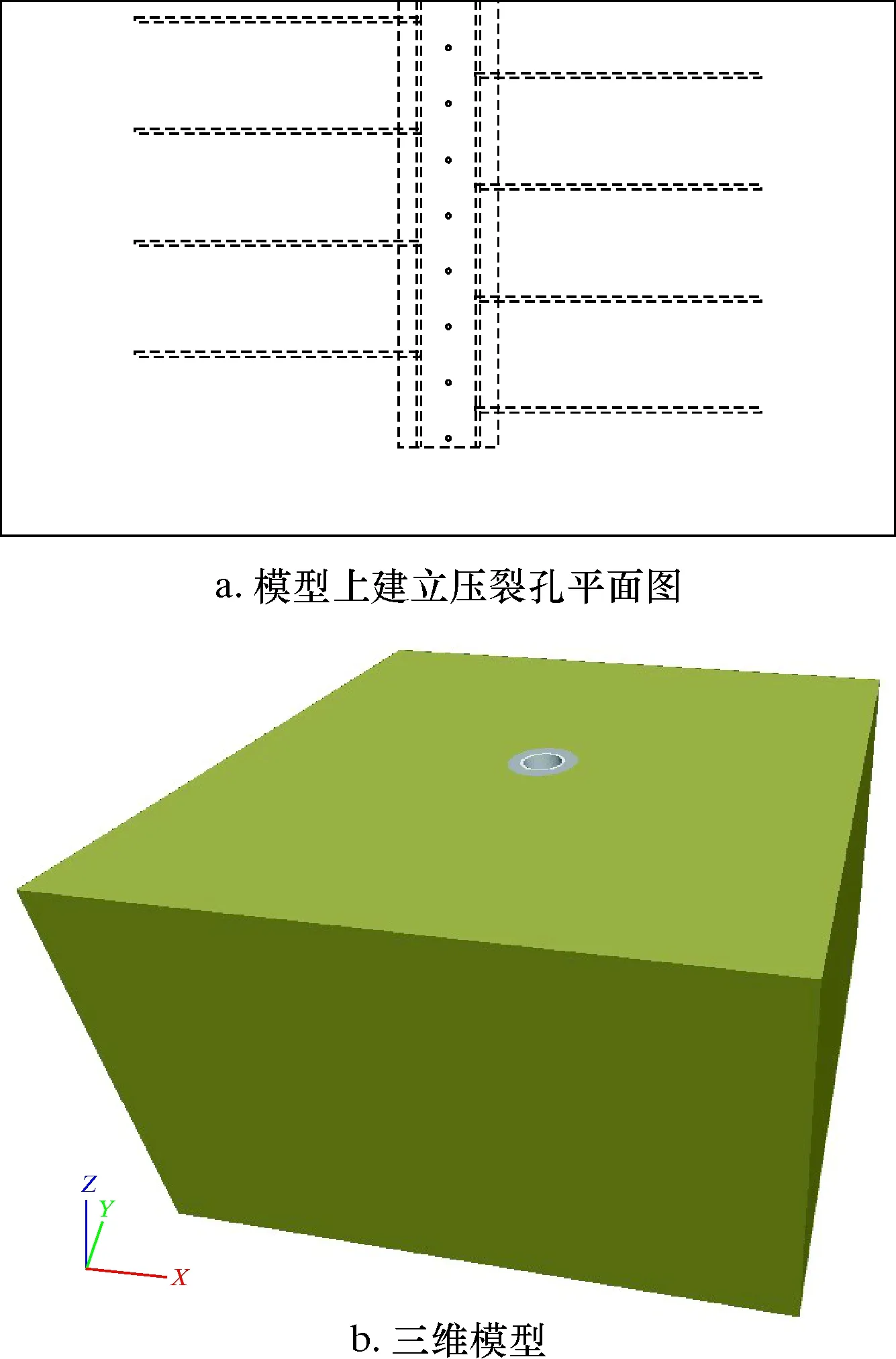
图1 射孔后储层-水泥环-套管模型图Fig.1 Post-perforation reservoir-cement sheath-casing model
2.2 属性分配与网格划分
将建立好的射孔后储层-水泥环-套管三维模型定义为mohr-coulomb模型,并对其进行网格划分。本文研究的主要是射孔段组合体中储层的应力状态分布情况,所以对未射孔结构区域的组合体模型的网格尺寸做放宽处理。对网格进行粗化处理可节省网格划分时间,提高模型的计算效率;对射孔段射孔孔眼区域的网格尺寸做加强处理并进行网格细化,提高模型的计算终止变形值,发现一共有330 781个单元节点、495 756个单元。网格划分结果如图2所示。

图2 网格划分结果Fig.2 Grid division results
2.3 边界条件设置
在模型下表面施加z方向的位移约束,模拟下部储层对模型的约束作用;在外表面施加x和y方向的位移约束,模拟外围储层对模型的约束作用;在模型的z方向施加σv,模拟上覆岩层对模型的挤压作用,以平衡地应力,使岩层的初始位移接近于0。
2.4 载荷施加
该井井深5 000 m,压力液密度1.2 g/cm3,由式(1)可得σv=60 MPa。在模型z方向上表面施加60 MPa的上覆压力,压裂液从套管注入,压裂泵压为80 MPa。
3 初始应力分析
计算终止变形值δ设置为10-4时,储层的初始地应力场云图如图3所示。从图3a可以看出,储层在z方向的初始应力值从上到下逐渐增大,且该模型表面的压力约为60 MPa,与实际工况下σv=60 MPa相符。从图3b和图3c可知,储层在x方向初始应力值与在y方向初始应力值相同。

图3 计算终止变形值设置为10-4时储层的初始地应力场云图Fig.3 Cloud chart for initial ground stress field of reservoir when calculation termination deformation value is set to 10-4
3.1 不同计算终止变形值对z方向地应力的影响
不同计算终止变形值下初始地应力场z方向应力云图如图4所示。从图4可以看出,随着计算终止变形值的减小,初始地应力场z方向的最大地应力值变化不大。z方向最大地应力值随计算终止变形值的变化曲线如图5所示。
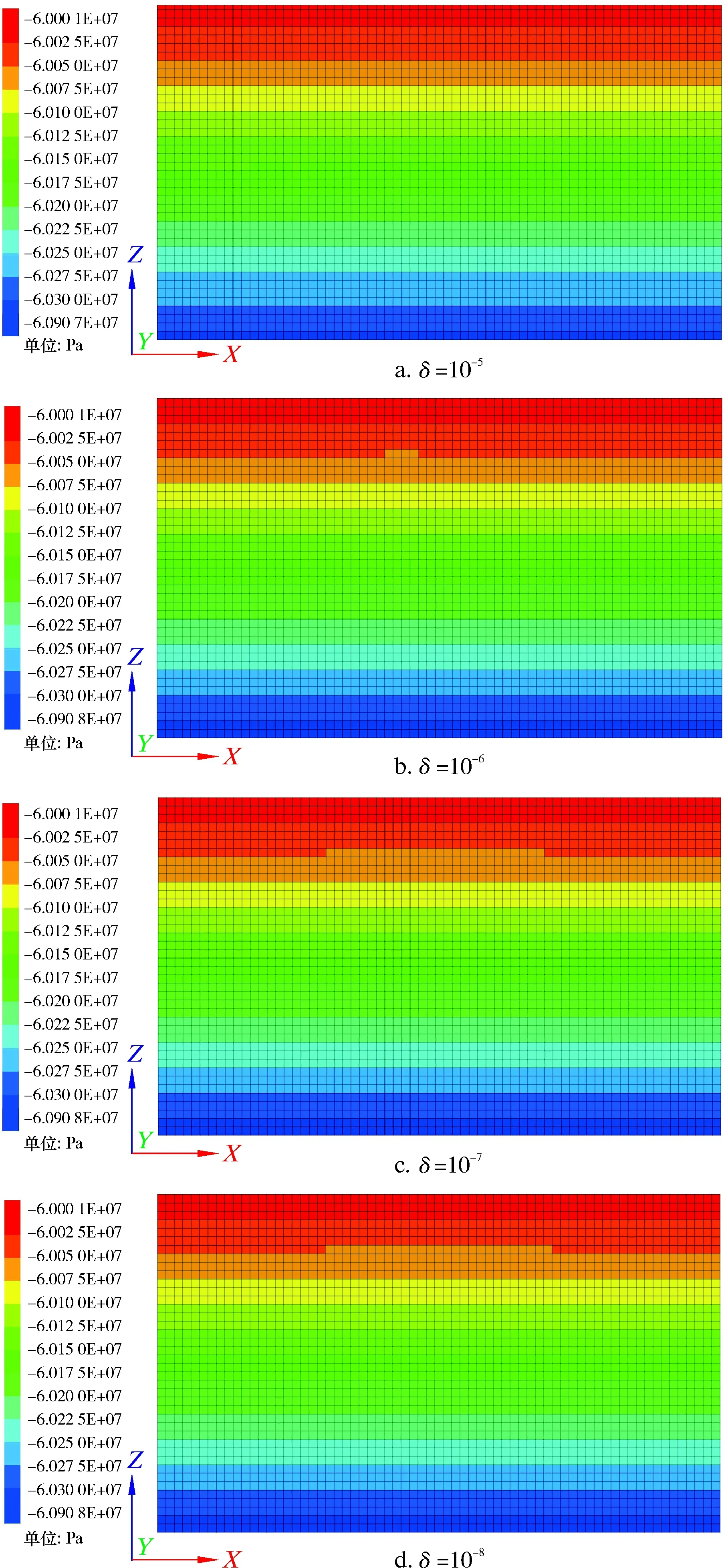
图4 不同计算终止变形值下初始地应力场z方向应力云图Fig.4 Stress cloud chart in z direction of initial ground stress field under different calculation termination deformation values
从图5可以看出:z方向最大地应力值随计算终止变形值的减小而趋于稳定状态;计算终止变形值设置为10-4时,z方向最大地应力值为60.29 MPa;计算终止变形值设置为10-8时,z方向最大地应力值为60.91 MPa,二者地应力相差1.10%,即计算终止变形值的缩小对初始地应力场z方向的地应力产生的影响不大,计算终止变形值越小,初始地应力场z方向的最大地应力值越趋于稳定状态。
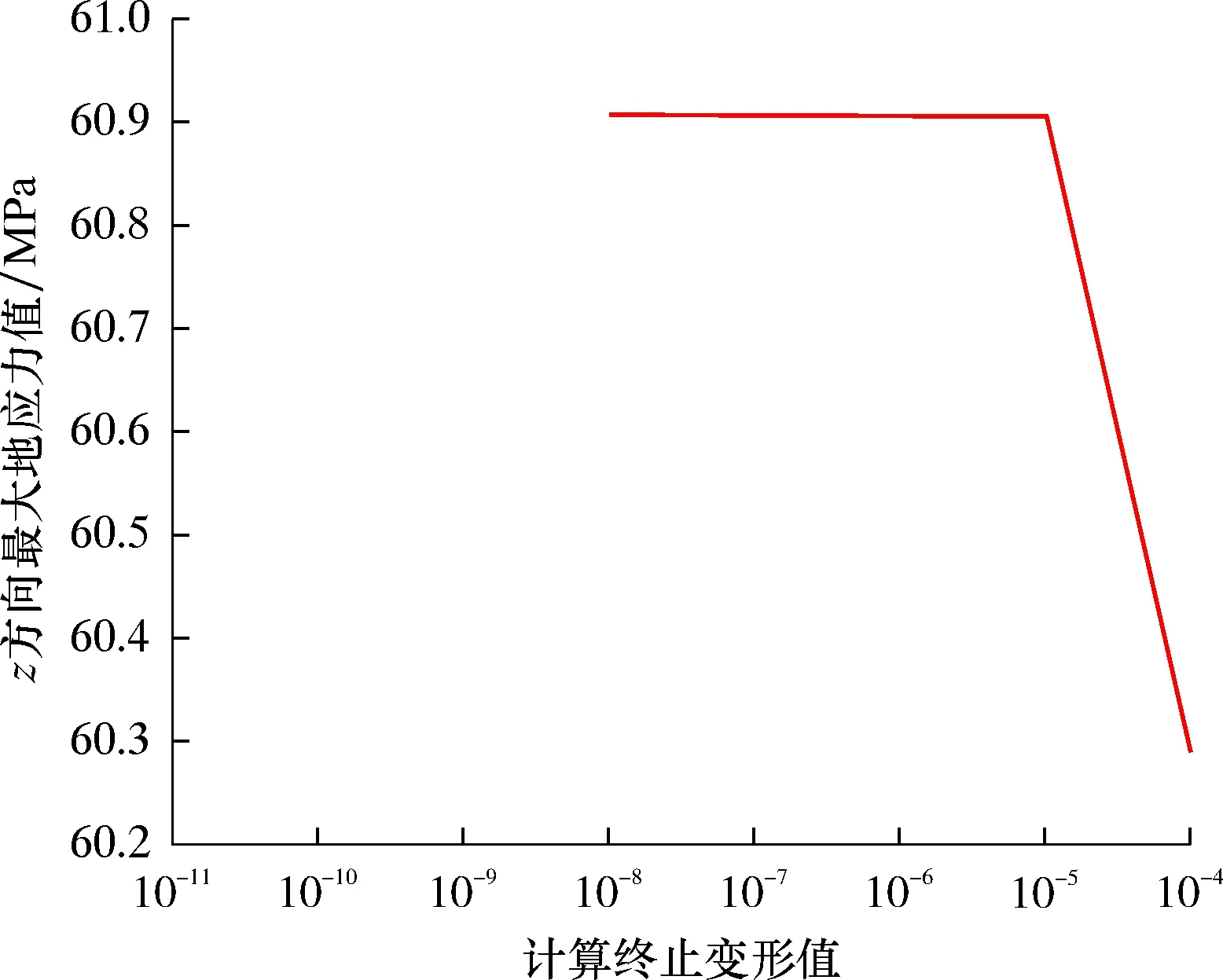
图5 z方向最大地应力值随计算终止变形值的变化曲线Fig.5 Variation curve of maximum ground stress value in z direction with calculation termination deformation value
3.2 不同计算终止变形值对x方向地应力的影响
不同计算终止变形值下初始地应力场x方向应力云图如图6所示。从图6可以看出,随着计算终止变形值的减小,初始地应力场x方向的最大地应力值变化不大。x方向最大地应力值随计算终止变形值的变化曲线如图7所示。从图7可以看出:x方向的最大地应力值随计算终止变形值的增高而趋于稳定状态;计算终止变形值设置为10-4时,x方向最大的地应力值为18.01 MPa;计算终止变形值设置为10-8时,x方向最大的地应力值为18.21 MPa,二者地应力相差1.11%,即计算终止变形值的缩小对初始地应力场x方向地应力产生的影响不大,计算终止变形值越小,初始地应力场x方向的最大地应力值越趋于稳定状态。

图6 不同计算终止变形值下初始地应力场x方向应力云图Fig.6 Stress cloud chart in x direction of initial ground stress field under different calculation termination deformation values

图7 x方向最大地应力值随计算终止变形值的变化曲线Fig.7 Variation curve of maximum ground stress value in x direction with calculation termination deformation value
3.3 不同计算终止变形值对y方向地应力的影响
y方向最大地应力值随计算终止变形值的变化曲线如图8所示。从图8可以看出:y方向的最大地应力值随计算终止变形值的减小而趋于稳定状态;计算终止变形值设置为10-4时,y方向最大的地应力值为18.01 MPa;计算终止变形值设置为10-8时,y方向最大的地应力值为18.21 MPa,二者地应力相差1.11%,即计算终止变形值的减小对初始地应力场y方向地应力产生的影响不大,计算终止变形值越小,初始地应力场y方向的最大地应力值越趋于稳定状态。
将图5、图7、图8与图3相比较可以发现,计算终止变形值的减小对初始地应力场各个方向地应力产生的影响不大,即计算终止变形值越小,初始地应力场各个方向的最大地应力值越趋于稳定。
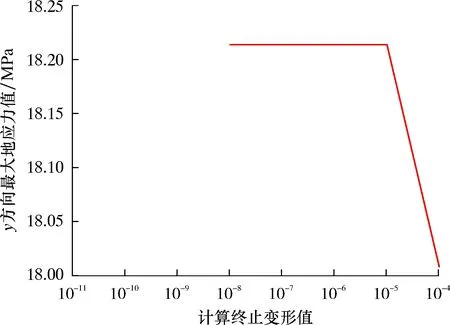
图8 y方向最大地应力值随计算终止变形值的变化曲线Fig.8 Variation curve of maximum ground stress value in y direction with calculation termination deformation value
4 压裂工况下地应力分布分析
压裂泵压为80 MPa时地应力云图如图9所示。

图9 压裂泵压为80 MPa时地应力云图Fig.9 Ground stress cloud chart at 80 MPa fracturing pump pressure
从图9可以看出:在压裂过程中,压裂液注入储层中,致使储层中初始地应力场发生改变,z方向的地应力最大值在螺旋式的16个小孔周围,其值为129 MPa;x与y方向水平最大应力值都在井筒内壁,其值分别为13.79和17.80 MPa。
4.1 不同压裂泵压对z方向地应力的影响
不同压裂泵压下的z方向地应力云图如图10所示。从图10可以看出,随着压裂泵压的逐渐增大,z方向最大地应力值有上升的趋势。z方向最大地应力值随压裂泵压的变化曲线如图11所示。从图11可以看出:随着压裂泵压的逐渐增大,z方向最大地应力值有上升的趋势,并逐渐趋于稳定状态;压裂泵压分别为65、80和95 MPa时,z方向最大地应力分别为105、129和133 MPa;泵压增加23%时,地应力增加23%;泵压增加19%时,地应力增加3%,即压裂泵压的增大对z方向的地应力产生了明显的影响。
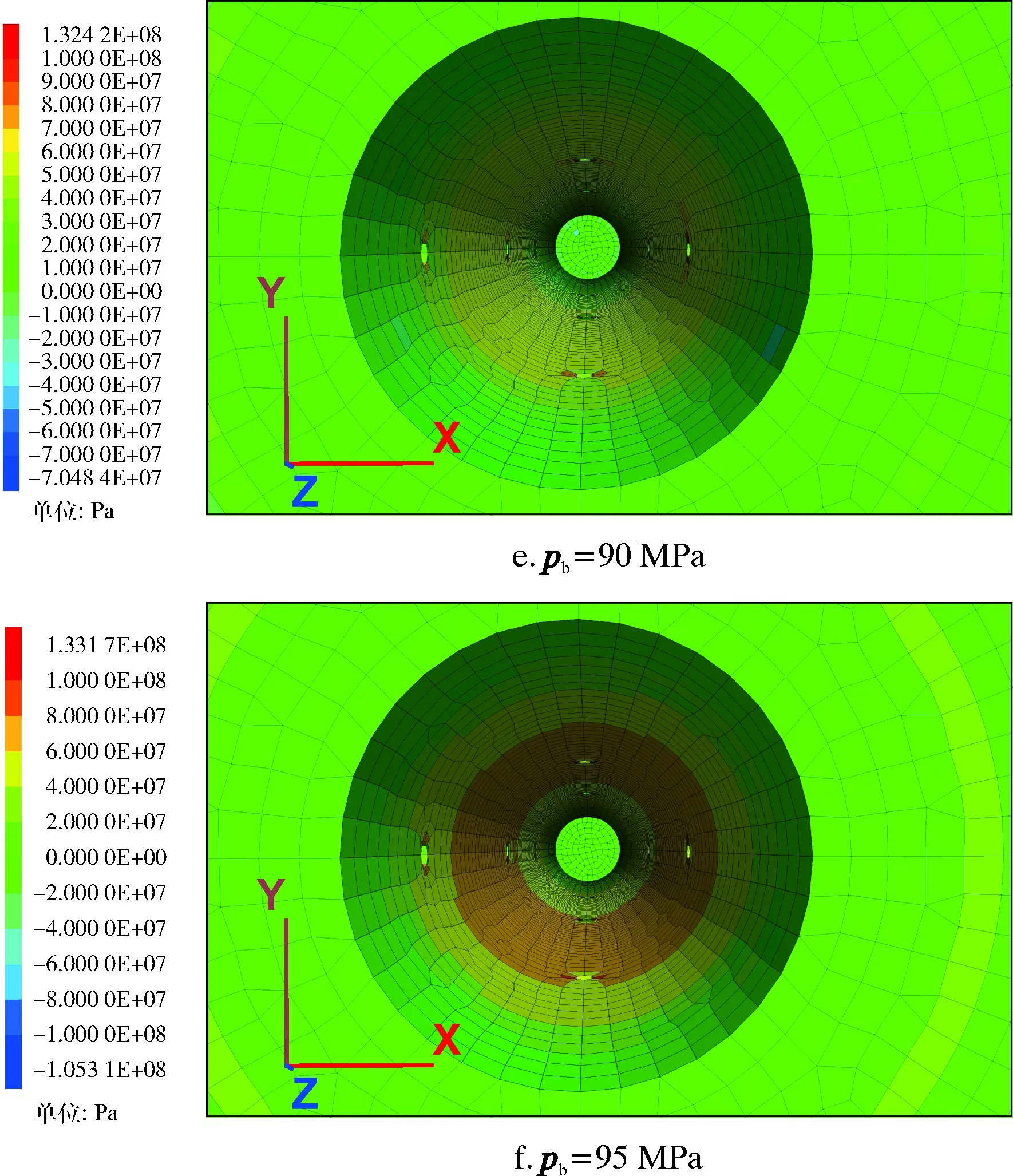
图10 不同压裂泵压下z方向的应力云图Fig.10 Stress cloud chart in z direction under different fracturing pump pressures
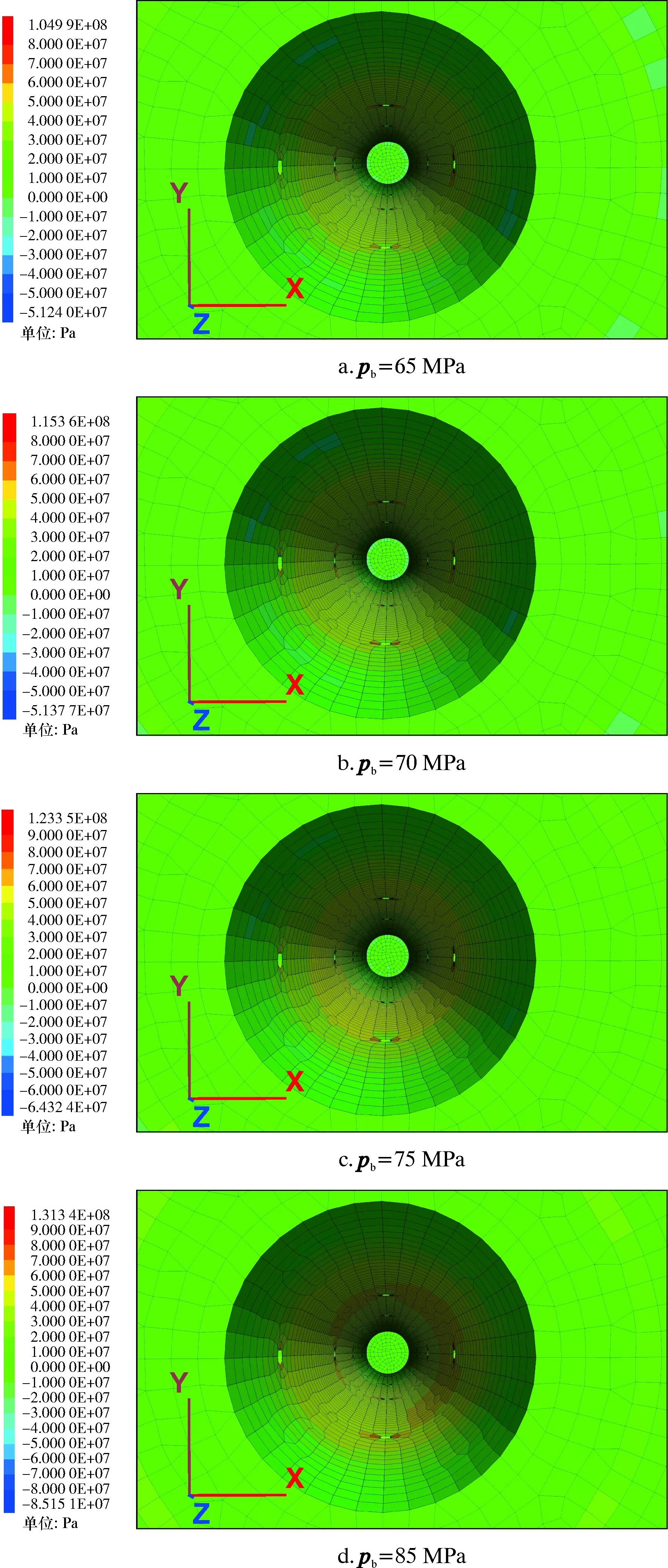
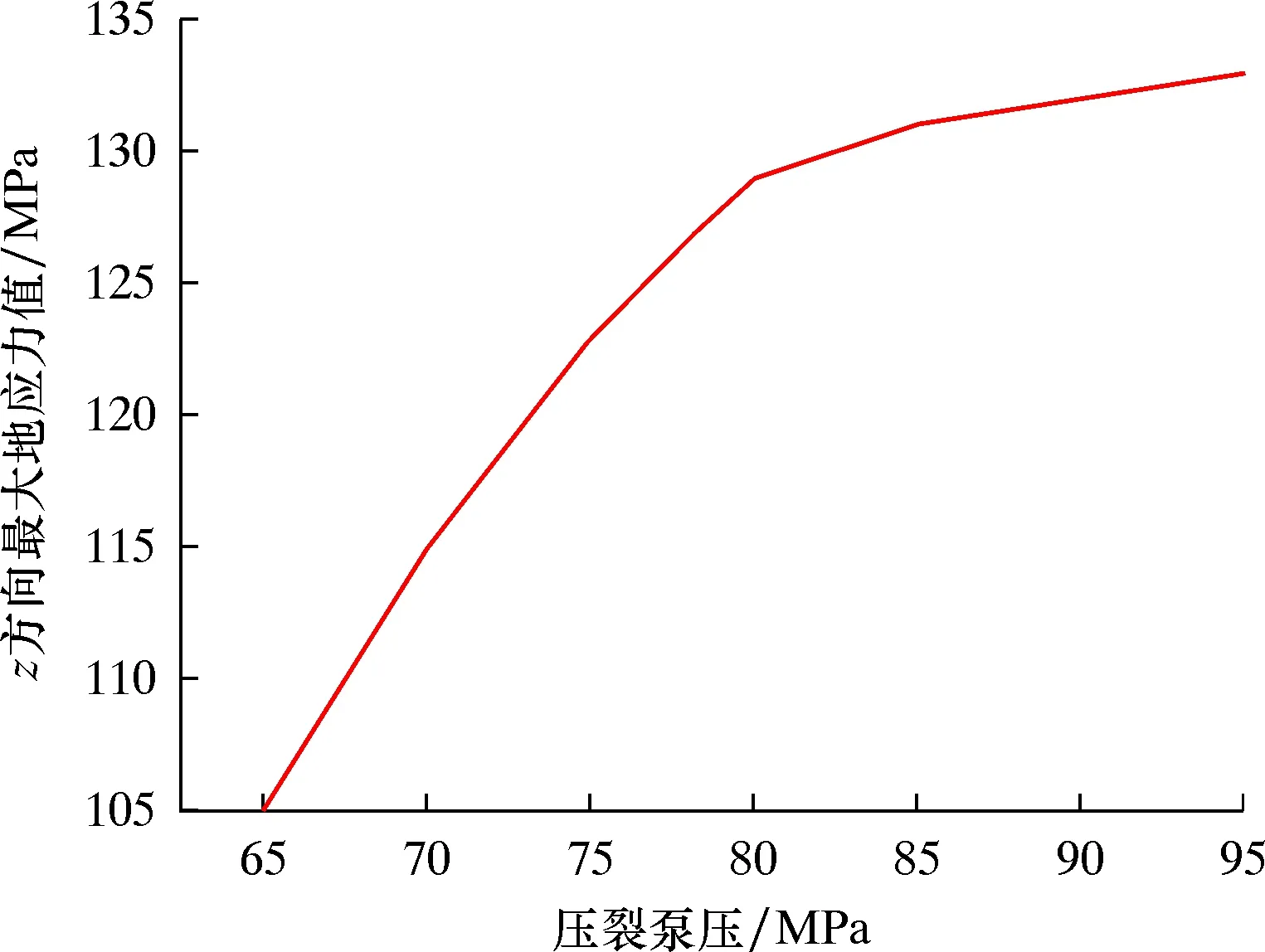
图11 z方向最大地应力值随压裂泵压的变化曲线Fig.11 Variation curve of maximum ground stress value in z direction with fracturing pump pressure
4.2 不同压裂泵压对x方向地应力的影响分析
不同压裂泵压下的x方向地应力云图如图12所示。从图12可以看出,随着压裂泵压的逐渐增大,x方向最大地应力值有上升的趋势。x方向最大地应力值随压裂泵压的变化曲线如图13所示。
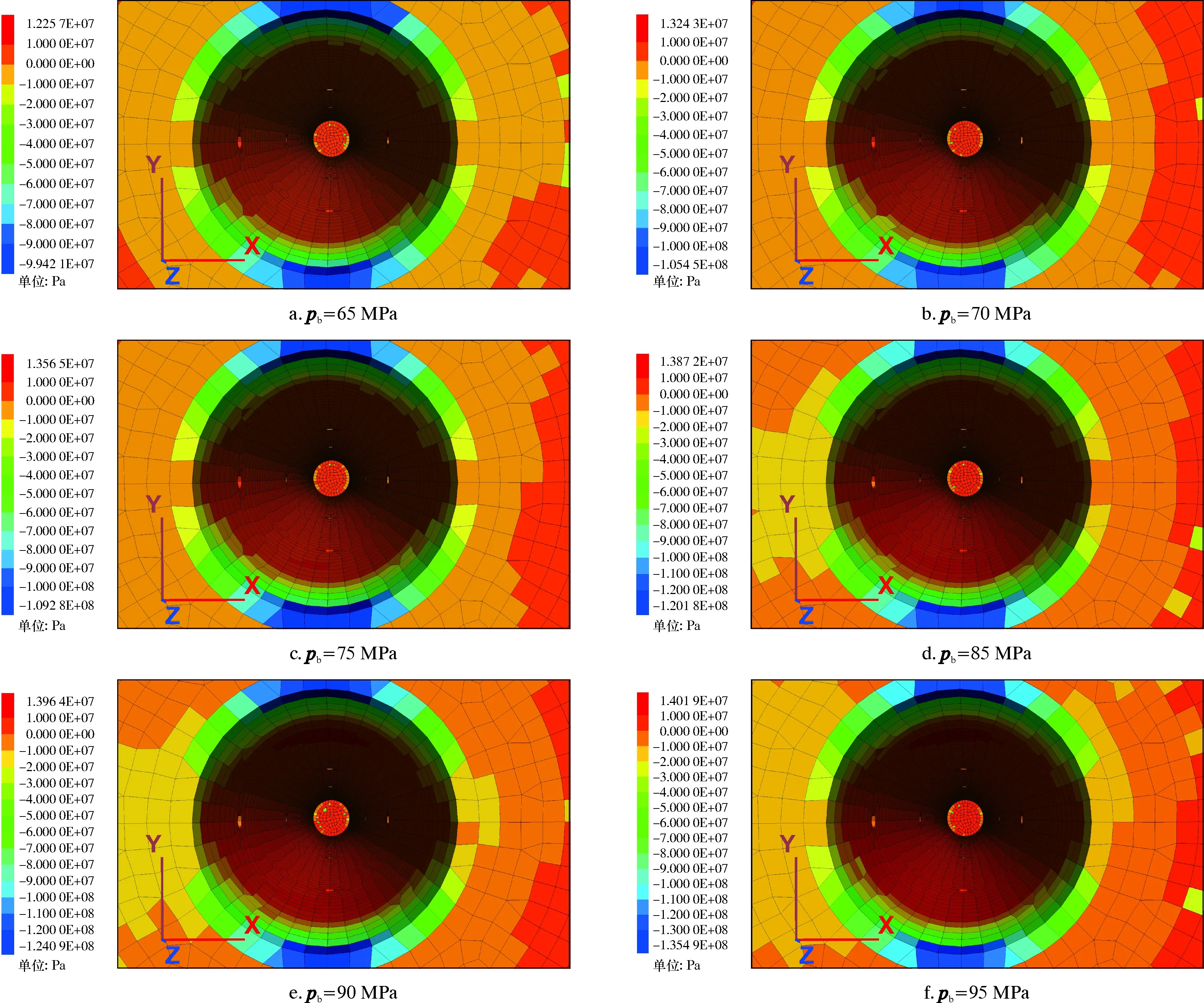
图12 不同压裂泵压下的x方向应力云图Fig.12 Stress cloud chart in x direction under different fracturing pump pressures
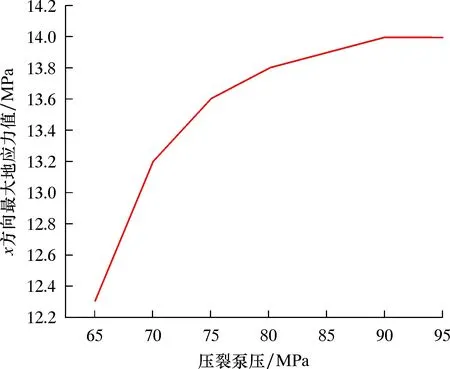
图13 x方向最大地应力值随压裂泵压的变化曲线Fig.13 Variation curve of maximum ground stress value in x direction with fracturing pump pressure
从图13可以看出:随着压裂泵压的逐渐增大,x方向最大地应力值有上升的趋势,并逐渐趋于稳定状态;压裂泵压分别为65、80和95 MPa时,x方向最大地应力分别为12.3、13.8和14.0 MPa;泵压增加23%时,地应力增加12%,泵压增加19%时,地应力增加1%,即增大压裂泵压可使x方向最大地应力值也增加。
4.3 不同压裂泵压对y方向地应力的影响
y方向最大地应力值随压裂泵压的变化曲线如图14所示。从图14可以看出:随着压裂泵压的逐渐增大,y方向最大地应力值有上升的趋势,并逐渐趋于稳定状态;压裂泵压分别为65、80和95 MPa时,y方向最大地应力分别为16.4、17.9和18.1 MPa;泵压增加23%时,地应力增加9%;泵压增加19%时,地应力增加1%,即增大压裂泵压,y方向最大地应力值也会增加。
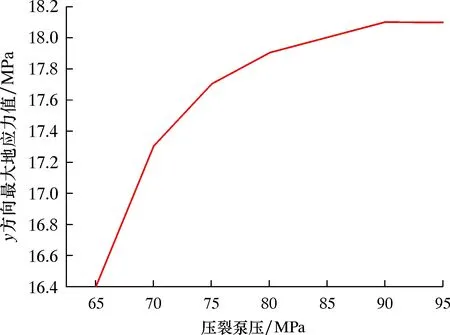
图14 y方向最大地应力值随压裂泵压的变化曲线Fig.14 Variation curve of maximum ground stress value in y direction with fracturing pump pressure
将图11、图13、图14与图3相比较可以发现,压裂液高压泵入储层,使储层中本来平衡的地应力发生破坏,导致地应力重新分布。因此,在压裂工况下工作时,本文方法可提高压裂工况下地应力的预测精度,为套管强度安全性分析提供载荷依据。
5 结论与建议
本文应用弹性力学理论和地应力叠加原理,结合隐式/半隐式有限差分分析方法,以实际井为例建立了射孔后储层-水泥环-套管模型,分析了储层初始地应力场,模拟压裂过程,分析了压裂泵压对地应力重新分布的影响,得到如下结论:
(1)计算终止变形值设置为10-4时,z方向最大地应力值为60.25 MPa, 计算终止变形值设置为10-8时,z方向最大地应力值为60.91 MPa,二者地应力相差1.10%,即计算终止变形值越小,初始地应力场z方向的最大地应力值越趋于稳定状态。
(2)压裂泵压分别为65、80和95 MPa时,z方向最大地应力分别为105、129和133 MPa,泵压增加23%时,地应力增加23%,泵压增加19%时,地应力增加3%,即压裂泵压的增大对z方向的地应力产生了明显的影响。压裂工况会使储层中本来平衡的地应力发生破坏,导致地应力重新分布。
(3)压裂泵压对储层地应力的影响较大。本文的研究方法可提高压裂工况下的地应力预测精度,为套管强度安全性分析提供载荷依据。
