一种轧辊静压轴承主动控制方法①

谢磊 计江 师浩浩

（中国重型机械研究院股份公司 陕西西安710032）

1 前言

高精密轧机由于高精度、高转速、高柔性和高效率等特点在特种带材生产过程中应用越来越广泛，为现代制造业增添了强劲的动力，是重型机械制造业的重要组成部分［1－5］。轧辊作为高精密轧机的核心部件，对轧机的轧制速度、轧制精度、轧制力、轧制能耗、轧材规格等具有直接重要的影响，而静压轴承又是支撑轧辊承受径向载荷最直接的部件。因此，静压轴承的性能将直接影响高精密轧机的运行状态。

随着高精密轧机的轧制速度越来越高、功率的越来越大，生产上对降低振动、提高轧辊稳定性的要求日益剧增，被动地改善轴承性能的方法已经不能满足工程使用要求［6－7］。于是，人们提出了主动控制轴承的概念，即根据轴承和转子的实际运行状态主动控制改变轴承的承载力等性能。目前，最常见的有电磁轴承、流变流体轴承等。

KY Lum等人［8］成功地将电磁轴承应用于刚性转子的自对中控制，但是高速时的控制效果不佳。Z Yu等人［9］利用电磁轴承控制挠性转子的振动，仿真结果表明电磁轴承可以有效地抑制简单转子的同频振动。汪希平等人［10］研究了电磁轴承支承的高速转子系统的动力学特性。Nikolajsen JL等人［11］将电流变阻尼器用于抑制柔性转子的振动，取得了很好的减振效果。姚国治等人［12］设计了用于转子振动控制的多层挤压型电流阻尼器和开／关控制器，通过对悬臂转子系统的实验发现，随外加电压的增大，这种阻尼器能有效地抑制转子系统的临界共振，又不会引起系统的失稳。Zhu Changsheng等人［13］将挤压油膜阻尼器的间隙内冲入磁变流体，发现该阻尼器轴承的动特性很容易由简单的磁场控制，且能有效地抑制转子系统的振动。H Urretal等人［14］将磁流变体作为径向动压滑动轴承的润滑剂，理论和实验结果均表明该动压轴承的动静特性得到明显改善。

主动控制轴承采用闭环控制器，即根据监测系统采集到的转子运行状态，通过一定的控制算法，产生合适的控制信号改变轴承的润滑状态。在主动控制轴承中，控制器的性能优劣直接影响主动轴承的使用效果。传统的PID控制器因其结构简单、易于调节等优点在工业领域得到广泛应用，但是PID控制属于典型的线性控制方法，仅适用于线性系统小扰动场合，对于参数不断变化的非线性时变系统，PID控制器往往不能满足控制要求［15－17］。在主动静压轴承中，控制器的性能优劣直接影响到其控制效果。主动静压轴承是个复杂多变的非线性系统，其模型参数不断变化甚至无法确定，经典的线性控制器已不再适用于静压轴承轴心位置的控制［18－20］，因此，本文选用具有自学习能力的基于BP神经网络的PID控制器，仿真分析了主动静压轴承的轴心控制效果。

2 主动控制策略概述

主动静压轴承的轴心控制过程如图1所示。在该系统中，控制器根据主轴轴心的位移偏差信号，由一定的控制算法计算出最优的输出电信号，用于控制电液伺服阀的输出流量。电液伺服阀接收控制信号，输出与之成比例的流量进入静压轴承的油腔，实现油腔压力的调节。

图1 主动静压轴承的轴心控制过程原理图

对于滑动轴承支承的主轴系统的动力学研究，大都是将滑动轴承的油膜力简化为八个线性化的油膜刚度、阻尼系统，此方法仅适合于静态平衡位置附近的小扰动情形。主动静压轴承是个复杂多变的非线性系统，其刚度阻尼系数不断变化，它的模型参数也不断变化，甚至无法确定，因此无法建立精确的数学模型来描述该系统。同时经典控制理论的研究对象是具有准确数学模型的单变量线性定常系统，不适于控制具有非线性和不确定性的系统。

基于主动静压轴承的运动特点，所选用的控制器必须响应快，无超调或超调量很小，而且能根据控制对象本身参数或周围环境的变化，自动调整控制器参数以获得合适的输出。据此，本文选用基于BP神经网络的PID控制器。

PID控制器要取得良好的控制效果，就必须调整好比例系数kp、积分系数ki和微分系数kd三个系数间的关系。这三个系数间的组合有无穷多种，因此需要从无穷的非线性组合中找出最佳的组合。神经网络应用于PID控制器的系数选择是目前的一大研究热点。因为神经网络具有很好的逼近非线性映射能力，而且具有自学习、自组织、并行处理特征和有很强的容错能力和联想能力，适用于对复杂的非线性系统进行建模和控制。所以，本文选用基于BP神经网络的PID控制器，通过BP神经网络对被控系统性能的学习，在线实时调整kp，ki，kd三个基本参数。

3 基于BP神经网络的PID控制方法

基于BP神经网络的PID控制器结构如图2所示，它由两部分构成：

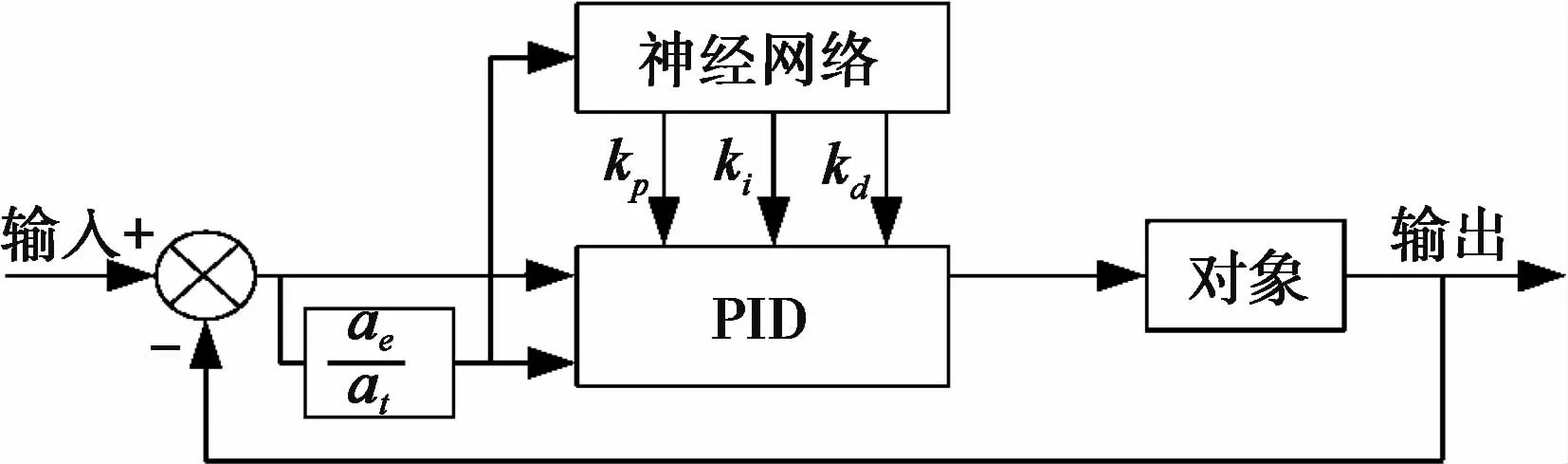
图2 基于BP神经网络的PID控制器结构

（1）经典的PID控制器，直接对被控对象进行闭环控制，其参数kp，ki，kd由神经网络在线调整；

（2）神经网络，由被控对象的实时状态，通过神经网络的自学习调整加权系数，改变kp，ki，kd三个参数，以实现输出性能指标的最优化，神经网络的输出层的输出对应于PID控制器的三个参数kp，ki，kd。

经典增量式数字PID的控制算法为：

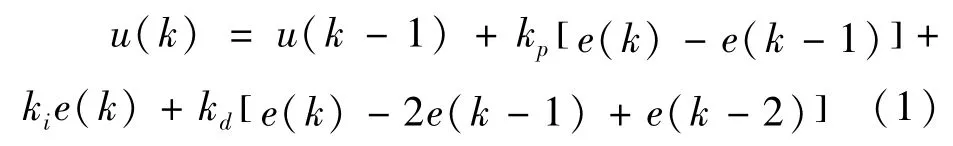
式中：kp，ki，kd—分别为比例、积分、微分系数；

u—控制器的输出；

e—误差信号。

选用三层式BP神经网络，其结构分为输入层、隐含层和输出层，BP神经网络结构如图3所示。

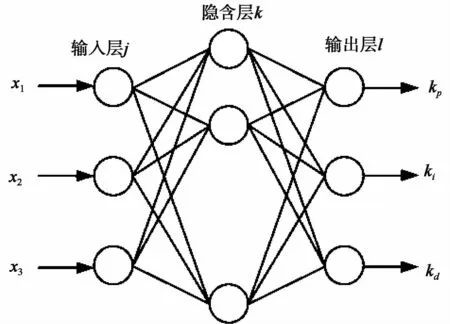
图3 BP网络结构

BP网络输入层的输入为x（j），输出为：

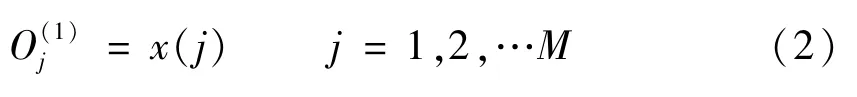
式中：M—输入层变量的个数，M的值由被控对象的复杂程度决定。

隐含层的输入、输出分别为：

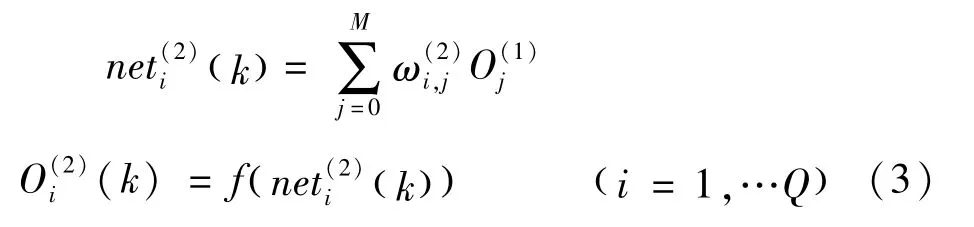
（1）、（2）、（3）—神经网络的输入层、隐含层和输出层。

隐含层神经元的活化函数f（x）选取对称的Sigmoid函数，即：

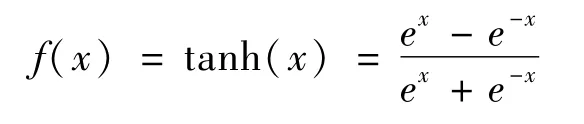
输出层的输入、输出分别为：

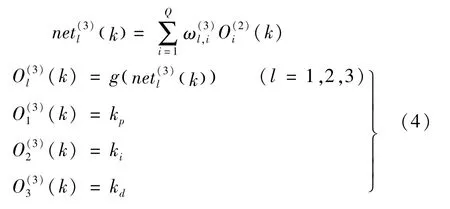
输出层的三个输出节点分别对应PID控制器的参数kp，ki，kd。由于kp，ki，kd不能为负值，所以输出层神经元的活化函数g（x）选取非负的Sigmoid函数：

取性能指标函数为：

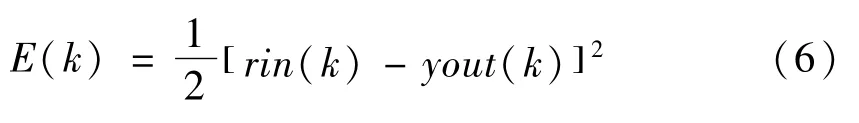
在控制过程中，需要不断地修正BP神经网络各层的加权系数。在BP神经网络中按照梯度下降法修正加权系数，按E（k）对加权系数的负梯度方向搜索调整，并附加一个全局极小的惯性项，使得搜索能快速收敛。

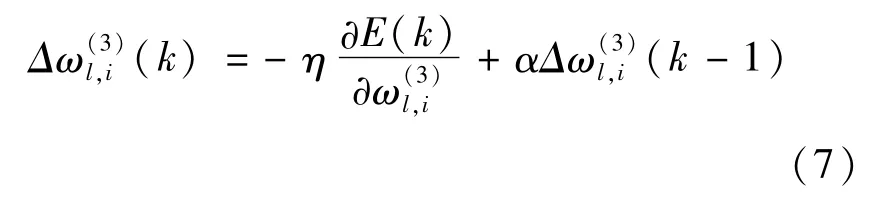
式中：η—学习速率；

α—惯性系数。

由式（1）和式（4），可求得

通过上述分析可得到输出层加权系数的学习算法为：

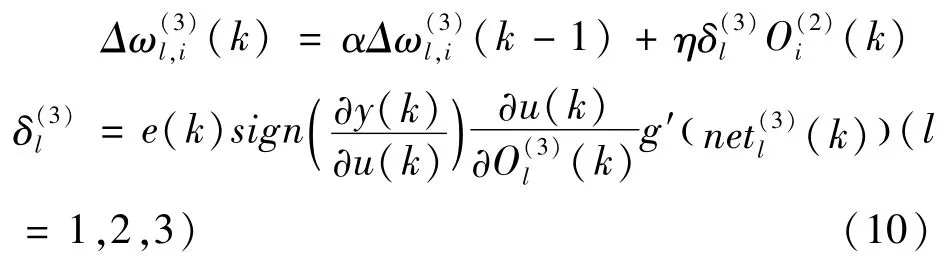
同理可得隐含层加权系数的学习算法为：

4 仿真结果及分析

以某轧辊支撑用静压轴承为例，本文分别仿真分析了两种外力作用下的传统静压轴承和主动静压轴承的响应情况，仿真用的轴承结构参数如表1所示。

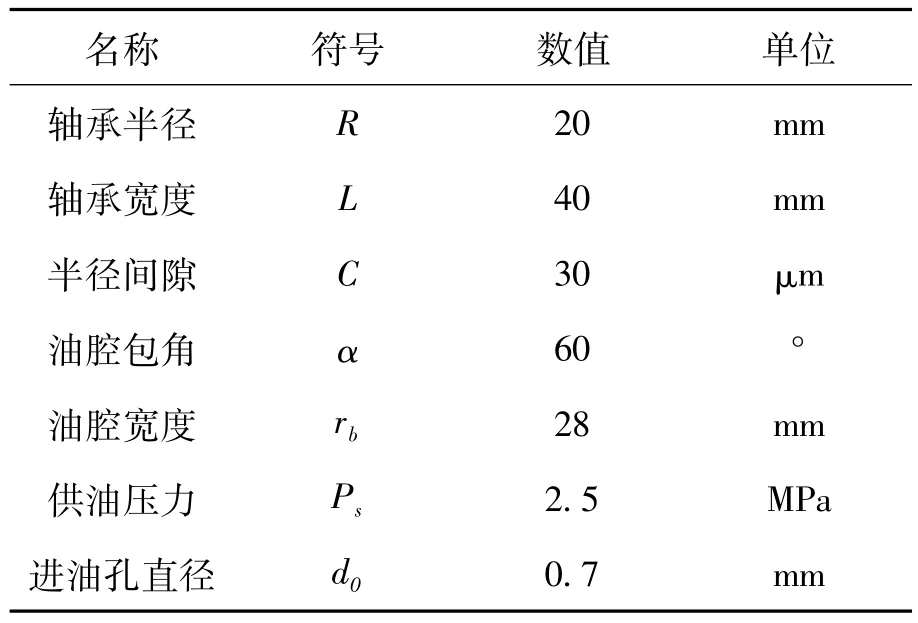
表1 静压轴承的基本参数

采用MATLAB建立该型号轴承的动力学模型，仿真分析时选取的主轴转速为2000r／min，轴颈的期望位置为轴承中心，外载荷在水平和垂直方向的分力相等：

（1）恒定外力（F＝400N，800N）；

（2）恒定外力中含有离心力扰动。

4.1 恒力作用

图4给出了在恒力作用下的该型号静压轴承的瞬态响应仿真结果。从图4中看出，该型号静压轴承在外力作用下产生了很大的偏心，因此轧制过程中已设定好的轧辊和带材间的相对位置发生改变，轧机的加工精度也会降低，并且增大外力，静压轴承的偏心量也会相应的增大。而由图5表示的主动静压轴承的瞬态响应仿真结果可看出，主动静压轴承能将恒力作用下的轴颈迅速调整到期望位置并保持稳定，如图5所示，并且调整时间很短，即使增大外力，主动静压轴承也能取得很好的控制效果，这样就保持了轧辊和带材间的相对位置，提高了轧机的加工精度。

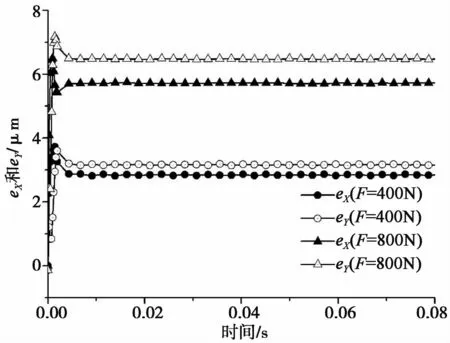
图4 恒力作用时静压轴承的瞬态响应

图5 恒力作用时主动静压轴承的瞬态响应

4.2 含离心力扰动的外力作用

在轧机轧制过程中，由于轧辊质量分布不均匀或带材的质量、硬度分布不均，轧制力就无法保持恒定不变。本文假设轧制力中所存在的扰动力为离心力，仿真分析传统静压轴承和主动静压轴承分别在式（12）、式（13）所示的两种外力作用下的响应。

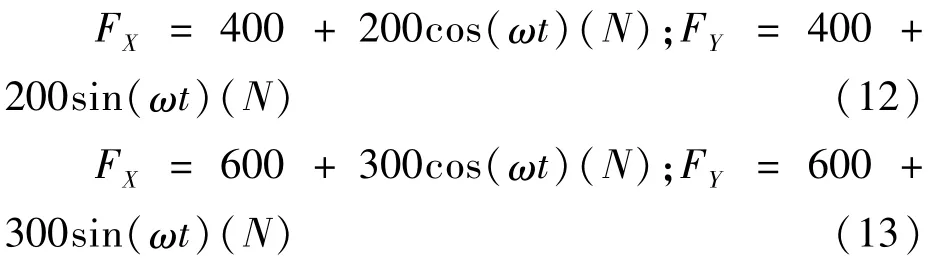
图6表示了在含离心扰动的外力作用下的主动静压轴承和传统静压轴承的瞬态响应，图7给出了相应的稳态响应轨迹。由图6和图7中可以看出，在外力作用下传统静压轴承的轴心在偏离轴承中心约4μm处涡动，涡动半径非常大，并且随着外力的增大，轴心的涡动半径也会相应的增大。而具有主动控制能力的主动静压轴承，能迅速将轴心调整到轴承中心附近，涡动半径明显减小，约为0.5μm。对比图6中的（a）（b）两图发现，当外力增大时，主动静压轴承始终在轴承中心涡动，涡动半径也很小，所以，在轧制不同材料的带材或选取不同的加工参数时，主动静压轴承能够抑制扰动力对轴心位置的影响，因此能保持轧辊和带材间的相对位置，提高了轧机的加工精度。

图6 不同外力作用时轴承的瞬态响应

图7 不同外力作用时轴承的稳态响应轨迹

5 结论

（1）介绍了轧辊静压轴承的主动控制基本策略和基本原理，在讨论了几种主动控制轴承方法的优缺点后，根据主动静压轴承的运动特点，本文选用了基于BP神经网络的PID控制器。

（2）详细论述了基于BP神经网络的PID控制器的结构和控制算法，基于MATLAB软件，已建立的静压轴承动力学模型和控制过程原理图，得到了主动静压轴承轴心控制性能的仿真结果。

（3）以某轧辊支撑用静压轴承为实例进行分析研究，将主动静压轴承与传统静压轴承的响应进行了比较，发现在外力作用下，主动静压轴承能迅速地将轴颈稳定到轴承中心附近，从而验证了本方法在进行轧辊静压轴承主动控制的有效性和精确性。因此，采用本方法论述的静压轴承来支承轧机轧辊，可以显著地提高轧制的轧制精度。