2005-2018年黄河三角洲景观格局脆弱性的时空变化规律
2021-08-09宋雨桐张子璇牛蓓蓓李新举
宋雨桐, 张子璇, 牛蓓蓓, 李新举
(1.山东农业大学 资源与环境学院, 山东 泰安 271018; 2.土肥资源高效利用国家工程实验室, 山东 泰安 271018)
景观格局变化是指由于土地利用方式不同导致的景观类型和景观格局的时空变化[1]。早期景观格局的主要研究方法包括传统的定性描述法、景观生态图叠置分析方法等。自20世纪90年代以来,随着经济社会的不断发展,人类活动强度增大,土地开发与土地利用方式的转变都对景观格局研究提出了新要求,同时3S技术的快速发展和应用,使得景观生态学的研究重点开始转向景观格局脆弱性及其动态变化的研究。景观格局脆弱性研究起源于生态脆弱性研究,1905年由美国学者Clements提出,随着相关研究的进一步深入,生态脆弱性的内涵也发生了变化,从单一研究方向转向多元化,由此衍生出景观格局脆弱性的研究[2]。景观格局脆弱性反映景观生态系统所受到的干扰及其脆弱程度[3]。国内外学者从多个方面对不同区域景观格局脆弱性展开了研究。主要从景观脆弱度指数[4]、土地利用类型变化[5]、地形因子[6]、脆弱性评价体系构建等[7]角度开展。目前针对黄河三角洲景观格局脆弱性的国内外研究较少,国外方面主要从3S技术[8-9]角度展开。国内方面主要运用景观指数分析法、构建生态环境评价体系等[10-12]方法对黄河三角洲景观格局的演变趋势及脆弱性展开研究,对探析景观格局演变规律,开展生态环境脆弱区的保护研究做出了贡献。景观格局分析主要以栅格数据作为数据源进行研究[13]。因此,选择适宜的粒度和尺度对景观格局的分析十分重要。Benson等[14]、秦岭等[15]、王朋冲等[16]通过不同粒度大小的栅格数据比较得出研究区景观格局研究的最适宜分析粒度。王璐等[17]、张金茜等[18]通过变异系数、最佳研究尺度模型的构建得出研究区最适宜分析尺度。但现有研究大都从粒度或尺度出发,对于粒度尺度的综合分析研究较少。
黄河三角洲地理位置特殊,近年来受人类活动、黄河水沙变化、海水侵蚀等影响,生态环境较为脆弱,景观类型变化复杂、剧烈,景观演变速度逐渐加快[19]。因此,开展景观格局及其脆弱性的研究能一定程度掌握区域景观格局变化机制及脆弱性的区域特征,为区域可持续发展和生态修复提供科学依据。
鉴于此,本研究以Landsat遥感影像为数据源,以监督分类得到的景观类型数据为基础,通过计算景观格局指数,运用变异系数和地统计方法,在确定最佳空间分析粒度和尺度基础上,探究黄河三角洲地区景观格局脆弱性时空分异特征及其空间关联性,以期可为生态脆弱区景观格局的研究提供一定的科学依据。
1 研究区概况
黄河三角洲是中国三大河口三角洲之一,位于莱州湾西岸和渤海湾南岸,是黄河携带大量泥沙淤积所形成的冲积平原,是中国最年轻的土地。本文选择黄河三角洲所处的东营市东营区、垦利区、河口区和利津县为研究区(37°16′—38°0′N,118°06′—119°18′E),总面积为5 962.64 km2。黄河三角洲属暖温带大陆性季风气候,四季分明,雨热同期,平均年降水量530~630 mm,多集中于夏季[20]。土壤类型受人为和自然因素影响存在较大差异,以潮土、盐土为主。黄河入海口处还成立了国家级自然保护区,该区具有中国最完整、最广阔的河口新生湿地,在全球湿地生态系统和珍稀物种保护方面都有不可替代的作用。
2 数据来源与研究方法
2.1 数据来源
本研究所使用的2005,2012,2018年黄河三角洲Landsat遥感影像数据均下载自地理空间数据云网站(http:∥www.gscloud.cn)。为保证分类的准确性,选择5月成像质量好、地物层次丰富、无云的影像。后在ENVI 5.3中对三期影像进行辐射定标、大气校正、几何精矫正,裁剪等预处理,参考黄河三角洲的区域特征和已有分类成果,采用最大似然法对预处理后的影像进行监督分类,将研究区划分为耕地、林地、草地、未利用地(包括盐碱地)、水域、建设用地、滩涂、盐田和养殖池8种景观类型。对不确定的图斑进行实地踏勘并修正,3期影像分类结果的kappa系数均在85%以上,符合精度要求,表明分类结果能够为本次研究提供数据支持。
2.2 研究方法
2.2.1 景观格局变化分析
(1) 构建景观类型转移矩阵。景观类型转移矩阵可以在时间上和空间上展示出景观类型的转移方向和变化幅度。将得到的景观类型分布图在ENVI中运用change detection statistics分别获取2005—2012年,2012—2018年景观类型转移矩阵,利用转移矩阵对黄河三角洲景观类型变化过程进行定量分析。
(2) 计算景观类型动态度。动态度常用来表示特定时间内某种土地利用类型的数量变化情况,可以定量描述其变化幅度与变化速度[21]。动态度计算公式如下:
(1)
式中:i为第i类景观类型;t1,t2为研究时间点,Ki为t1到t2时段内第i类景观类型的动态度;Sit1,Sit2为t1,t2时间第i类景观类型的面积。
2.2.2 景观格局最佳分析粒度的确定
(1) 变异系数法选取敏感性指数。变异系数是衡量序列观测值离散程度的相对统计量[22]。本研究运用变异系数法判定各景观指数对空间粒度变化的敏感程度,随着景观空间粒度的增加,若某一景观指数的变异系数随之增加,则说明该景观指数对空间粒度的敏感性较高,且变异系数越大,敏感性越高,反之亦然。本研究首先在ArcGIS中将研究区各年份景观类型矢量数据栅格化,每个年份均得到28幅不同空间粒度大小(30~300 m)的景观类型数据。然后从景观水平和类型水平两个层面,从面积—边缘指数、形状指数、多样性指数、聚集度指数4个方面选取具有代表性的景观格局指数进行变异系数的计算并选出敏感指数。其中景观水平选取了景观面积(TA)、斑块个数(NP)、斑块密度(PD)、最大斑块指数(LPI)、边缘密度(ED)、斑块相似度指数(LSI)、平均斑块面积(SHAPE-MN)、面积周长分维数(PAFRAC)、蔓延度指数(CONTAG)、相似临近比(PLADJ)、散布与并列指数(IJI)、斑块凝聚度(COHESION)、景观分裂指数(DIVISION)、分离度指数(SPLIT)、香农多样性指数(SHDI)、香农均匀度指数(SHEI)、聚合度指数(AI)17个景观指数;类型水平上选取了斑块类型面积(CA)、斑块个数(NP)、斑块密度(PD)、最大斑块指数(LPI)、边缘密度(ED)、斑块相似度指数(LSI)、平均斑块面积(SHAPE-MN)、面积周长分维数(PAFRAC)、相似临近比(PLANDJ)、散布与并列指数(IJI)、斑块凝聚度(COHESION)、景观分裂指数(DIVISION)、分离度指数(SPLIT)、聚合度指数(AI)14个景观指数。
(2) 拐点识别法。拐点识别法是通过分析各景观指数随粒度变化的趋势图来确定景观指数的适宜粒度的一种方法[23]。通过综合分析敏感景观指数随粒度变化的趋势图确定适宜粒度区间,根据趋势拐点来确定适宜的景观粒度。
2.2.3 景观格局脆弱性研究
(1) 半变异函数。半变异函数是指区域化变量考虑系统属性在所有分离距离上任意两样本间的差异[24]。通常认为区域化变量的空间异质性是由空间自相关和随机误差所引起的。本研究分别计算3个研究年份4个不同网格大小下的景观适应性指数LAI,利用GS+软件分别计算其半变异函数,根据半变异函数拟合模型参数确定黄河三角洲地区景观脆弱性分析的最适宜尺度。
(2)
式中:h为步长;N(h)是分隔距离为h时的样本总数,当h=0时,γ(h)=C0;C0称为块金值,表示随机因素产生的空间异质性;A0为变程用于表示空间相关性的作用范围,当h增大到A0时,γ(h)从非零值达到一个相对稳定的常数;C是结构方差,表示因空间自相关而产生的空间异质性;C0+C为基台值,表示自相关部分的空间异质性,其值大小与空间差异性成正比。
(2) 景观脆弱度计算。本研究通过构建景观敏感度指数LSI和景观适应性指数LAI得到景观脆弱度指数LVI[1],其计算公式见(3)—(5)。利用Fragstats和ArcGIS软件计算处理后得到不同研究年份的黄河三角洲景观脆弱度分布图。
(3)
LAI=PRD×SHDI×SHEI
(4)
LVI=LSI×(1-LAI)
(5)
式中:n为景观类型数目;i为景观类型;Ui为景观干扰度指数;Vi为景观类型易损度; PRD,SHDI,SHEI分别为斑块丰富度指数、香农多样性指数、香农丰富度指数。
(3) 空间自相关分析。空间自相关分析用来描述事物在空间上的依赖关系[25]。本研究借助GeoDa软件,来进行景观空间自相关分析。首先构建空间权重矩阵,再进行全局自相关和局部自相关分析。通过Moran’sI指数和局部自相关LISA显著图[26],探究不同研究年份研究区各网格单元景观脆弱度指数之间的空间相关性和某一网格单元与邻近网格单元景观脆弱度指数的空间关联程度。
3 结果与分析
3.1 景观格局动态变化
3.1.1 景观类型转移特征 黄河三角洲2005—2012年和2012—2018年的景观类型转移矩阵见表1—2。2005—2012年,未利用地和滩涂的转出面积,分别是555.90 km2,269.04 km2。占到了各自总面积的67.84%和57.56%,主要转移方向是耕地、建设用地、盐田和养殖池。耕地转出面积为416.93 km2,占总变化面积的25.61%,主要转移方向是建设用地。建设用地面积增加最多,7 a间增加321.32 km2,其次是盐田和养殖池,增加了310.05 km2。2012—2018年,依旧是未利用地和滩涂的转出面积最大,分别是236.13 km2,189.166 km2,盐田和养殖池、耕地、建设用地分别占未利用地转出的31.59%,40.05%,16.73%,而滩涂的主要转移方向是盐田和养殖池,占其总转出面积的59.74%。面积增加最多的仍然是建设用地,增加了283.45 km2,占建设用地总面积的26.71%。盐田和养殖池增加的面积仅次于建设用地为252.32 km2。综合来看,建设用地的面积增加了2.33倍,这与近年来黄河三角洲城市化进程加快以及经济发展的需求有关。2005—2018年黄河三角洲未利用地和滩涂的转出幅度最大,两者面积分别较2005年减少20.08%和41.51%,土地利用率提高。林地和草地的总面积基本保持不变,但转入转出较为频繁。水域面积基本稳定。

表1 2005-2012年黄河三角洲景观类型转移矩阵 km2

表2 2012-2018年黄河三角洲景观类型转移矩阵 km2
3.1.2 景观动态度分析 黄河三角洲景观类型在研究时段内呈现出不同的变化特点,景观类型动态度见图1。由图1可知建设用地、盐田和养殖池面积大幅增加。建设用地在两个研究时段内的动态度分别为10.06%,10.01%,呈现持续增长态势,且增长速度最快。2018年盐田和养殖池面积是2005年的2倍,增长速度先快后慢,其中滩涂和未利用地持续减少,减少速度加快,在2012—2018年,动态度分别达到了-6.84%和-9.40%。这表明黄河三角洲地区经济的快速发展使得城镇化进程持续推进,土地利用效率提高。林、草地的总面积基本保持不变,草地面积的增加基本来自于林地的转化,原因是研究区土地盐渍化比较严重树木相对难以存活往往转化成荒草地或者沼泽。

图1 2005-2018年黄河三角洲单一景观类型动态度
耕地面积先增加后减少,动态度为0.74%和-1.4%,这与一开始的扩大耕地规模以满足生产需求为主要发展模式转变为人与自然和谐发展的政策有关。水域动态度较小,为-1.70%和0.24%,研究时段初期水体转出方向主要为耕地,但到后期耕地转换为水体基本达到了一个动态的平衡。
3.2 景观格局最佳空间分析粒度
3.2.1 景观水平上最佳空间分析粒度确定 本研究通过变异系数法判断各景观指数对空间粒度的敏感程度,根据景观指数的变异系数大小,将敏感度分为5个等级,分别为极高敏感度(变异系数>10%),高敏感度(变异系数7%~10%),中敏感度(变异系数4%~7%),低敏感度(1%~4%),不敏感(变异系数<1%)。变异系数计算结果见表3。
由表3可知,NP,PD,LPI,ED,LSI,DIVISION,SPLIT这7个指数是景观水平上的极高敏感指数。且3个年份中,2012年各个景观指数的变异系数整体较高,因此选用2012年的数据进行研究区最佳空间分析粒度的趋势分析。

表3 2005-2018年黄河三角洲景观水平景观指数随粒度变化变异系数 %
2012年7个敏感指数随粒度的变化趋势见图2。可以看出,随着空间粒度的增加,景观指数的变化主要分为3类:第一类特征是随着空间粒度的增加,景观指数先快速降低然后缓慢降低,包括NP,PD;第2类是随着空间粒度的增加基本保持同一斜率缓慢下降,包括ED,LSI;第3类是先基本保持平稳然后随着空间粒度的增加上下波动,达到到某一空间粒度时又恢复到稳定状态,包括LPI,DIVISION,SPLIT。

图2 2012年黄河三角州景观水平上敏感景观指数随粒度的变化趋势
由图2可知,NP,PD无明显的“拐点”,但达到200 m粒度后下降的速率明显降低;ED,LSI也没有明显的拐点;DIVISION,SPLIT,LPI在110~220 m粒度区间内波动明显。因此,从景观水平上综合分析景观指数的拐点认为,黄河三角洲整体的适宜粒度区间为220~300 m。
3.2.2 类型水平上最佳空间分析粒度确定 为了保证研究的准确性,类型水平上最佳分析粒度的确定同样重要。与景观水平的研究思路一致,以2012年为例,选取了CA,NP,PD,LPI,ED,LSI,SHAPE-MN,PAFRAC,PLANDJ,IJI,SPLIT,COHESION,DIVISION,AI这14个景观指数进行不同空间粒度大小下变异系数的计算。其变异系数计算结果见表4。
由表4可知,类型水平上不同景观类型的景观格局指数表现出不同的敏感度,所有景观类型均表现出极高敏感的指数有NP,PD,ED,LSI。同样,将各景观类型变异系数与空间粒度进行趋势分析,发现盐田和养殖池、水体的适宜粒度区间为190~300 m;滩涂、建设用地、未利用地、林地和草地的适宜粒度区间为200~300 m;耕地的适宜粒度区间为220~300 m。

表4 2005-2018年黄河三角洲不同类型水平景观指数随粒度变化变异系数 %
综合景观水平和类型水平的分析结果,黄河三角洲地区景观分析的最佳粒度范围为220~300 m,最终本研究选取220 m作为黄河三角洲最佳景观分析粒度。
3.3 黄河三角洲景观格局脆弱性时空演变规律
3.3.1 最优尺度的确定 景观格局脆弱性具有尺度效应,已有研究通常将网格划分尺度设置为是平均斑块面积的2~5倍[27],因此本研究将研究区划分为1.5 km×1.5 km,2.0 km×2.0 km,2.5 km×2.5 km,3.0 km×3.0 km 4种尺度的单元网格,通过分析不同网格尺度下景观适应性指数(LAI)的半变异函数参数特征,筛选景观格局脆弱性的最优分析尺度。3个年份不同网格尺度下景观适应性指数的半变异函拟合参数见表5。

表5 2005-2018年黄河三角洲不同网格尺度下景观适应性指数的半变异函数拟合模型
整体来看,3个研究年份不同尺度下的最佳模型均为指数模型。2.5 km和3.0 km尺度下的块金值较小,说明随机部分造成的空间异质性较少。由表5可知,2.5 km,3.0 km尺度下的空间变异程度较为合理,既能反映一定的差异性,又不会使差异性过于显著。C是结构方差,表示因空间自相关而产生的空间异质性。C/(C0+C)是结构方差与基台值的比例,C/(C0+C)越大,表示因自相关造成的空间异质性越多。由表5可知,各个尺度下的C/(C0+C)均大于75%,说明变量具有显著的空间相关性。A0表示变程,只有当网格大小小于变程时,才能保证研究区景观格局脆弱性的高度相关关系。由此可知2.5 km和3.0 km尺度更适宜探讨景观格局的空间异质性及关联性。相比而言,3 km尺度下函数复相关系数R2更高,综合残差RSS更小,因此3 km×3 km的网格是黄河三角洲景观格局脆弱性分析的最适宜尺度。
3.3.2 景观脆弱性时空特征分析 图3展示了基于3 km×3 km尺度的黄河三角洲景观格局脆弱度空间分布图,各脆弱度等级所占比例见表6。由图3可知,在研究时段内研究区景观脆弱度变化幅度不大,高度脆弱区大都分布在北部和东部沿海滩涂处,由于盐田和养殖池连片式分布,且景观类型以滩涂为主,使得景观优势度较低,从而导致景观敏感性较高。较高脆弱度分布在未利用地和建设用地上,其中以未利用地为主的较高脆弱区逐渐减少,而以城镇为主的地区呈逐年扩大趋势。中等脆弱度地区分布较为均匀,较低脆弱度和低脆弱度地区主要分布在研究区的中部、西部和南部。

图3 2005-2018年黄河三角洲景观格局脆弱度及其指数(LVI)分布特征
由表6可知,低脆弱度地区呈逐年减少趋势,研究时段内比例从14.38%下降到6.99%。这是由于为满足农业和城市化的发展,土地利用开发程度增加,景观破碎化增加。较低脆弱区、中等脆弱区呈增加趋势,所占比例分别增加了2.0%和3.0%。此外,2005—2018年黄河三角洲景观脆弱度呈现不同的空间变化特征,研究区北部的景观格局脆弱度有变好的趋势,但南部有恶化的趋势,这是因为北部未利用地土地利用结构不断优化,景观类型逐渐丰富,这对景观格局脆弱度有一定的缓和作用;而研究区中部和南部的垦利县、东营区和利津县,近年来建设用地逐渐扩张,破坏了原有的板块连通性,因此导致景观脆弱程度的提高。
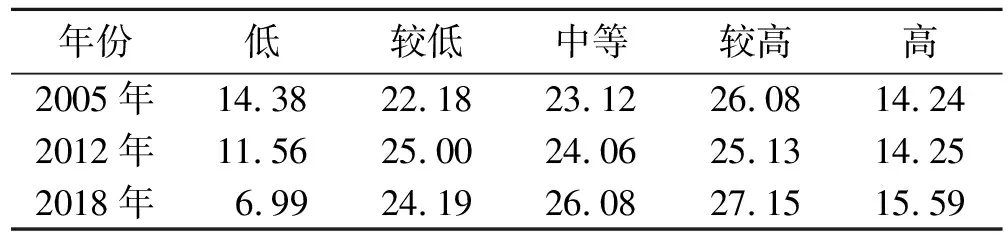
表6 2005-2018年黄河三角洲不同等级景观格局脆弱度网格所占比例 %
3.3.3 景观格局脆弱性的空间关联分析 2005,2012,2018年黄河三角洲的景观脆弱度指数全局Moran’sI结果如表7所示,3个年份的全局Moran’sI系数分别为0.354,0.365,0.399,且显著性水平均达到0.001,说明黄河三角洲景观脆弱度呈现显著的空间正相关关系,且相关关系持续增强,空间集聚现象日趋明显。

表7 2005-2018年黄河三角州景观格局脆弱度全局Moran’s I指数
选择局部空间自相关系数LISA作为度量指标,探究黄河三角洲不同方向上景观格局脆弱度的空间集聚模式(图4)。由图4可知,研究区以高—高集聚区、低—低集聚区为主。景观格局脆弱度高—高区主要集中在研究区北部和东部,这是由于北部和东部对应区域的中心单元均为高、较高脆弱区,景观类型主要以滩涂、盐田和养殖池为主,相邻单元正相关性强,对周边单元的辐射作用较强。高—高区分布范围先缩小后增加,表明景观格局脆弱性先有所缓解但又略微抬升。低—低脆弱区分布在中部和西南部,这与此区域景观类型分布较为均匀有关。同时低—低脆弱区的减少,主要是因为经济的快速发展、人为扰动增强,导致景观破碎度增加。

图4 2005-2018年黄河三角洲地区景观脆弱度LISA集聚特征
由图5 LISA显著性水平图分析可知,景观格局脆弱度高—高对应的显著性较强,P大都在0.001,0.01水平上,中部和西南部的低—低区显著性水平大都为0.5。

图5 2005-2018年黄河三角洲景观脆弱度局部自相关LISA显著特征
4 讨论与结论
4.1 讨 论
本研究以遥感影像为数据源,综合变异系数法、网格法、地统计等方法在确定最佳分析粒度的基础上选取最佳分析尺度,对黄河三角洲景观格局脆弱性展开研究,并进行空间自相关分析,从而揭示黄河三角洲景观格局在时间上和空间上的演变规律。目前关于黄河三角洲景观格局脆弱性的研究较少,本文能在一定程度上提高黄河三角洲景观格局研究的准确性,为景观格局脆弱性研究提供了新的思路。
数据源、空间粒度、尺度的不同都会对景观格局的研究结果产生影响。因此,本研究选取了2005,2012,2018年相同月份的Landsat遥感影像,避免了数据源不同引起的差异。合理确定研究区最佳分析粒度和尺度是保证景观格局脆弱性结果准确的前提条件。相较于其他文章仅从最佳粒度或最佳尺度一个方面展开研究,本研究综合确定了黄河三角洲分析的最佳粒度和尺度,提高了研究的准确性。很多学者采用拐点法来选择最佳分析粒度[18],也不乏有学者以信息损失最小为原则,运用信息损失评价法确定最佳分析粒度[28]。然而在最佳分析尺度的选取方面,很多学者通过综合分析研究区大小以及工作量的大小直接选取。同时,最佳粒度和尺度有很强的地域性,鉴于此,如何选取最佳空间粒度和空间幅度的方法仍需进一步研究。
影响景观格局脆弱性的因素有很多,例如气候条件、土壤类型、地形地貌、人类活动等。本研究受限于数据的可获得性,仅以遥感影像为数据源来探讨景观格局的脆弱性,缺乏景观脆弱性的影响因子方面的研究,研究结果尚不够全面。在后续的工作中,将从气候、地形、土壤类型、人类活动等多角度展开综合研究,从而更加全面的揭示研究区景观生态的演化特点和规律。
4.2 结 论
(1) 2005—2018年,黄河三角洲景观类型发生了较大幅度的改变,建设用地面积增加2.33倍,未利用地和滩涂面积大幅减少,分别减少了各自总面积的20.08%和41.51%。
(2) 景观水平和类型水平上,高敏感性的景观指数在粒度达到220 m后基本相对稳定,确定220 m是研究区最适宜的空间分析粒度。根据不同网格尺度下的景观适应性指数的半变异函数参数对比,确定3 km×3 km尺度是研究区最适宜的景观脆弱度分析尺度。
(3) 2005—2018年,黄河三角洲地区景观格局脆弱度逐渐增强,脆弱地区大都分布在沿海地区,主要是由于沿海地区景观系统主要为滩涂、未利用地、盐田和养殖池,景观集中连片分布导致景观适应性较低。内陆地区景观脆弱度也有所增强。
(4) 2005,2012,2018年景观格局全局Moran’sI逐年上升,说明3个时期景观格局脆弱度存在正相关现象。在总体空间分布上,2005—2018年黄河三角洲景观格局脆弱度均以高—高脆弱区与低—低脆弱区的聚集为主,且显著性水平相对较高。
