基于改进型Bug算法的林间移动平台避障方法研究

蔡存成，姚立健，曾松伟，柴善鹏，王露露

(浙江农林大学 a工程学院，b信息工程学院，浙江 杭州 311300)

林产品与生产物资的运输是林业生产的重要环节，目前传统机械化运输常采用轨道[1-2]、索道[3]和运输车[4]等方式，为适应高效作业的需求，自动化[5]、智能化[6]运输设备越来越受到研究人员的重视，自动导航技术对提高林间生产运输的效率和安全性具有重要意义[7]。由于林木生长位置无序，在制定导航路径时无法提前避开，因此避障成为解决林间自动导航问题的关键。

根据避障路径的规划方式，可将常用避障算法分为全局路径规划和局部路径规划[8]。全局路径规划算法中，机器人根据环境先验信息自主规划全部路径，但林间环境存在不确定性，无法提前获取准确的障碍物信息；局部路径规划算法有人工势场法[9]、启发式算法[10]和应激式算法[11-12]等，其中前2种算法分别存在局部最优解和计算死循环等问题，故路径规划容易失败。在应激式算法中，Lumelsky等[13]提出的爬虫(Bug)算法适用于未知环境，计算少且避障时效高，因而获得了较多关注；黄培奎等[14]提出了圆弧Bug算法和折线Bug算法，并分别进行半实物仿真试验验证了2种Bug算法的可行性；彭艳等[15]基于多爬虫(Multi-Bug)机制寻求避障路径，利用格栅法进行环境建模，并与多种算法做仿真试验对比，得出Bug算法路径更短、效率更高等结论；康亮等[16]将Bug算法与滚动窗口算法相结合，利用三次螺旋线对避障路径进行光滑化处理，得到机器人易于追踪的路径。上述Bug算法均在软件仿真中实现，由于该算法默认机器人是一个质点且具备全方位无死角探测能力，使其较难应用于实际[17]，因此较多学者进行了改进：代峰燕等[18]通过六边形拓补法和坐标建模法改进Bug路径规划算法，使油罐清洗机器人能在有障碍物的工况下降低清洗重叠率；江济良等[19]运用神经行为学原理改进Bug算法，依靠机器人生物触角非360°探测环境，实时激励并触发相应行为，能使机器人避障转向少、距离短；赵祚喜等[20]基于机器人非360°探测改进Bug算法，将分段直线与速度空间结合，得到绕行障碍物边缘的圆滑路径，并应用于实车进行试验。以上改进多基于超声传感器非360°探测，且实现成本较低，但均未对如何跟踪障碍物边缘进行专门讨论。良好的“边缘跟踪”能力可有效缩小避障范围，适用于狭窄的林间环境，但如何精准地进行“边缘跟踪”是一个难点[21]。模糊控制设计简捷、应用方便，常被用于避障控制中：Hacene等[22]利用5个超声波传感器采集机器人周围的环境信息，并采用模糊控制实现了移动机器人的避障，其中“墙体跟随”功能使机器人能够沿行墙体，但对非墙体障碍物跟随性较差；谭莲子等[23]利用多传感器融合技术，通过超声波、红外等传感器共同获取障碍物信息，使用模糊控制方法实现了轮式机器人的避障；金兆远等[24]将二分法和模糊控制相结合，使用6个超声波传感器组成超声波阵列，可获得较小的探测盲区，最终使机器人能够根据周围环境选择最佳避障路径进行避障。上述模糊控制均能较好地控制机器人避障，但忽视了输入变量权重对控制精度的影响，同时对避障路径的冗余问题也未进行深入讨论，因此仍有必要进一步研究与改进。

基于以上原因，本研究采用基于Bug原理的避障方法，使用纯追踪算法以实现精准的全局路径跟踪，在避障初期自动判断最佳避障时机并使用最大转向角度，然后采用自适应调节的模糊控制器控制平台绕障，以减少避障路径冗余，以期为提高林间移动平台避障效率提供参考。

1 林间移动平台硬件及控制系统

如图1所示，林间移动平台采用纯电动后驱前转向四轮机构，由48 V、20 A·h锂电池供电。平台大小(长×宽×高)为130 cm×70 cm×125 cm，轴距和轮径分别为85和32 cm。由L298N驱动器推动电动推杆(BMXL150，48 mm/s，250 N)实现前轮转向，最大转向角为40°，最小转向半径1.24 m。驱动器AQMD6020BLS驱动后轮直流电机，并通过减速器、差速器传动实现平台行驶。平台四周安装有4个KS102和2个KS109超声波传感器，用来探测平台与障碍物之间的距离，量程分别为13～796和0～1 126 cm，精度分别为1和0.1 cm，波束角分别为50°和10°，收发频率同为50 Hz。

1.天线；2.KS102超声波传感器；3.KS109超声波传感器；4.电动推杆；5.锂电池；6.推杆电机驱动器；7.GPS信号接收机；8.直流电机驱动器；9.主控制器；10.后轮直流电机1.Antenna;2.KS102 ultrasonic sensor;3.KS109 ultrasonic sensorr;4.Electric push rod;5.Lithium battery;6.Electric push rod driver;7.GPS signal receiver;8.DC motor driver;9.Main controller;10.DC motor图1 林间移动平台的结构Fig.1 Structure of forest mobile platform

图2中，林间移动平台使用Trimble BD982接收GPS(global position system)信号。主控制器(STM32 F767IGT6)读取各传感器信号，处理形成平台的位置、航向信息及其与障碍物的距离信息，并通过自动导航模型计算出前轮期望转向角，完成路径追踪和避障。前后轮均设有光电增量式编码器(MK6012-G-400BN-T526)，用以检测前轮实际转角和后轮实际转速，以实现对试验平台运动状态的精准闭环控制。

(x,y)为移动标签坐标，m；θ为航向偏差，(°)；PWM为脉宽调制；U为电控制电压，V；PCM为脉冲编码调制；α为前轮转向角，(°)；v为后轮速度，m/s；ls为超声波传感器探测到的障碍物距离，cm(x,y) is coordinate of moving tag,m;θ is heading deviation,(°);PWM is pulse width modulation;U is electric control voltage,V;PCM is pulse code modulation;α is front wheel steering angle,(°);v is rear wheel speed,m/s;ls is obstacle distance detected by ultrasonic sensor,cm图2 林间移动平台的控制系统框图Fig.2 Control system of forest mobile platform

2 改进型林间移动平台的避障方法

2.1 Bug避障原理及改进

Bug算法的原理是：机器人在追踪当前路径的同时通过传感器探测外部环境，若发现有障碍物，则沿障碍物边缘行驶，绕越障碍物后继续向终点前进。本研究的改进Bug算法如图3所示，将追踪全程划分为路径追踪、避行和绕行3个阶段，分别优化避行和绕行阶段的控制方法，以解决传统Bug算法难以实际运用的问题。

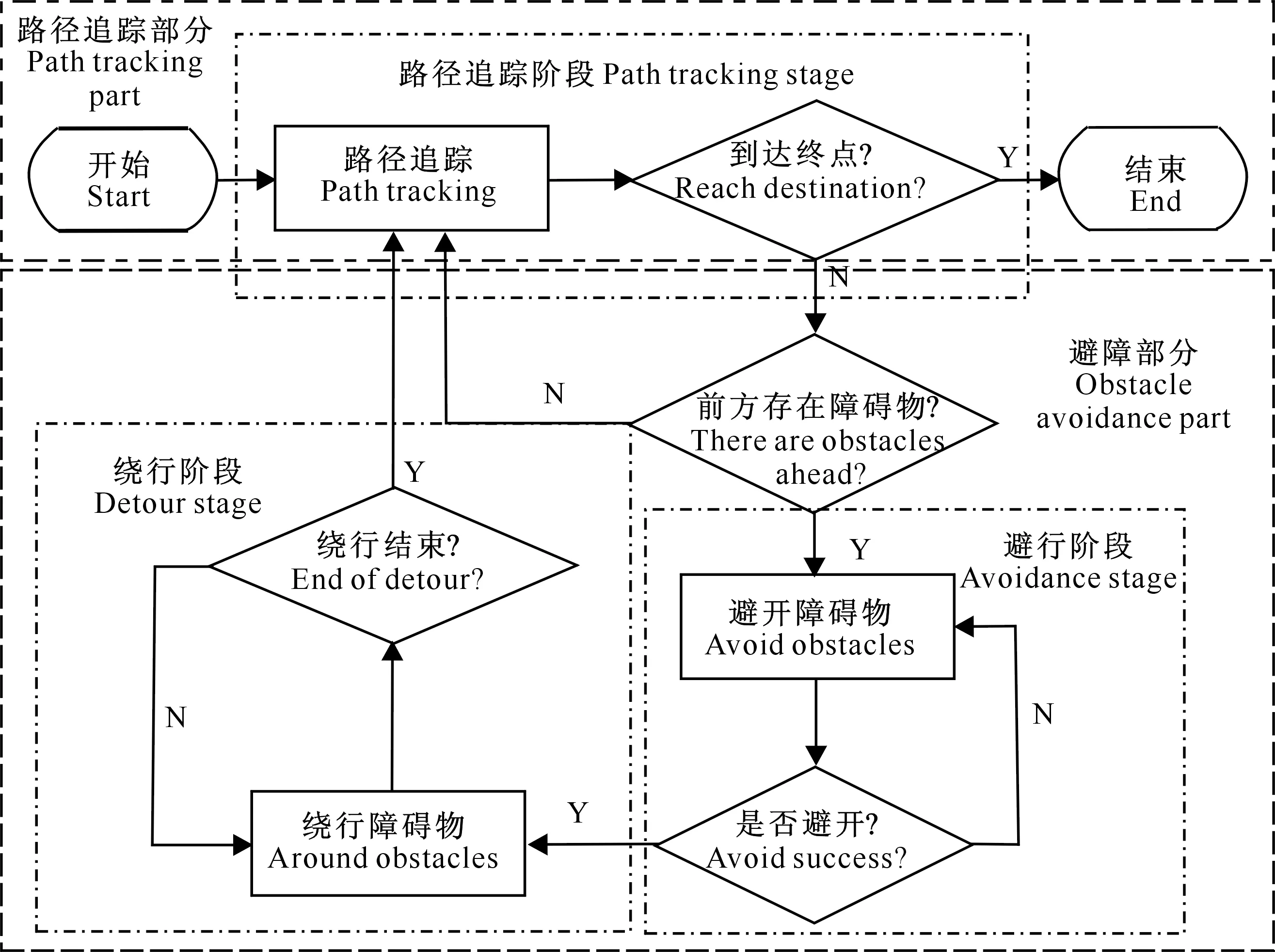
图3 林间移动平台的导航及避障流程Fig.3 Navigation and obstacle avoidance process of forest mobile platform

2.2 超声波传感器的布置

根据Bug算法的思想，将6个超声波传感器S1～S6分布于车身四周，用来模拟爬虫的触角，各传感器的安装位置及其探测区域如图4所示。

S1～S6为超声波传感器；A1～A6为探测区域；A1-2表示A1与A2重叠区域，A2-5、A1-6同理；阴影部分为盲区S1-S6 are ultrasonic sensors;A1-A6 are detection areas;A1-2 indicates overlapping area between A1 and A2,and A2-5 and A1-6 are the same.Shaded area is the blind area图4 超声波传感器的分布及其探测区域Fig.4 Distribution and detection area of ultrasonic sensor

各超声波传感器的具体分工为：S1、S2(探测距离13～200 cm)分别位于平台正前方，与平台前端能否安全避开障碍物密切相关，为获得更大的共同探测范围和更小的盲区，采用两波束的外缘平行的安装方式。S3、S4(0～80 cm)的波束角中心线与车身侧面垂直，主要负责侦测绕行障碍物时平台与障碍物的距离信息。S5、S6(13～330 cm)波束角的一边与车身侧面重合，负责监视车身两侧其余区域，以实现对车身周围的全覆盖探测。

2.3 避障策略

在图4的A1、A2区域中，由于单传感器无法对障碍物进行精确定位且这2个区域与探测盲区所在位置十分靠近，较危险，若障碍物出现在该区域内则停车。当障碍物出现在A1-2区域时，若平台直行则一定会发生碰撞，因此必须采取避行措施。当障碍物位于A3、A4区域时，使用模糊控制器严格控制该区域车-障距离，使平台沿障碍物边缘精准移动。A5、A6区域不包含与A3、A4重叠的部分，当障碍物出现在移动平台的侧面时，平台前轮转向角保持0°行驶，直至探测不到障碍物后再进行追踪路径。

对各区域影响避障决策优先级进行规定，即规定优先级次序为A1、A2>A3、A4>A1-2>A5、A6>A2-5、A1-6。若移动平台的左右两侧同时存在障碍物，则平台保持直行；若A1-2与两侧同时存在障碍物，则平台无法避开，应停车，其余情况都可根据优先级完成避障。

当所有区域都无障碍物影响行驶时，平台采用文献[25]的纯追踪导航模型进行路径追踪。

2.4 避行阶段最大转向角策略

2.4.1 避障转向角计算 如图5所示，当安装在车头的传感器S1和S2探测到障碍物P点时，平台右轮至少要以αmin的角度向左转向，平台的右前端点C才能“刚好”避开P点。根据几何知识，可求得αmin的计算公式为：

(1)

式中：K=(LBP+LCP+LBC)(LBP+LCP-LBC)×(LBP-LCP+LBC)(LCP-LBP+LBC)，LBP、LCP分别为S1、S2探测的障碍物距离，LBC、LCM、LMN为移动平台自身固定尺寸，可测量获取。为使式(1)进行有效计算并得到符合上述几何规则的转向角，必须保证以LBP、LCP为半径的弧线能在A1-2区域内相交，即满足：

(2)

图5 林间移动平台最大前轮转角的计算示意图Fig.5 Calculation of the maximum front wheel angle of forest mobile platform

2.4.2 转向响应速度测定 由于推杆固有速度限制及转向时地面对轮胎的阻力等因素，会造成前轮转向响应延迟，该延迟会影响避障的安全性和效率，因此需通过载荷试验掌握前轮实际的转向速度，为后期弥补措施做准备。通过给0.5 m/s恒速移动的平台施加100 kg载荷进行转向延时试验，结果如图6所示。

图6 林间移动平台前轮转向延时的测定Fig.6 Measurement of front wheel steering delay of forest mobile platform

由图6可知，实际转向角在一定时间后才到达期望转向角，并在期望转向角附近波动，该波动是推杆内闭环控制调节的结果，该行驶速度对行驶稳定性的影响可忽略不计。根据每次转向过程中实际转向角到达期望转向角的时间差和所转过的角度差，得到前轮每转1°所需的平均时间为0.045 s。通过该转向速度可根据车速和所需转向的角度，得到转向期间移动平台的理论移动距离，其中最大移动距离为90 cm。

2.4.3 最大转向角转向时机的确定 根据式(1)、(2)，计算障碍物在移动平台正前方A1-2区域中任一位置时所需的最小转向角。以传感器S1、S2的距离信息为横、纵坐标轴，以对应的最小转向角为坐标值，建立如图7所示前轮转向角索引图。图7中转向角正负号根据“左转为正，右转为负”的原则确定。由图7可知，在图的右上角区域，即障碍物与平台距离较远时，所需的转向角较小，反之则较大。

为减少避障过程中的路径冗余，提高避障效率，移动平台需在尽可能靠近障碍物时，以最大转向角转向。根据式(1)可以得到转向角达到最大值时S1和S2的多组距离组合，将这些组合反映在图7中，会形成2条相交的曲线。考虑到平台转向的延迟，实际转向时机应该“提前”，即这2条曲线应向右上角移动90 cm，此时2条曲线会被拉长。如图8所示，2条绿色曲线将转向角索引图分为蓝、红两部分，当车-障距离位于蓝色区域时，平台保持路径追踪行驶;当车-障距离一旦到达绿色曲线处，立刻使用最大转向角避障；红色部分为危险转向区域，当车-障距离在该区域内时，平台会因转向延时而不能及时避开障碍物，因此需停车。

图7 林间移动平台转向角索引图Fig.7 Index map of steering angle of forest mobile platform

2.5 绕行阶段自调节模糊控制

当平台沿障碍物边缘行驶时，为兼顾平台与障碍物以尽可能小的距离“紧贴”同时又避免相撞，特设计一种带自调节函数的模糊控制器。通过构建车-障距离(lz)与预设绕行距离(绕行时平台与障碍物的理想距离)的偏差、车-障距离变化率和前轮转向角之间的对应关系，利用函数动态调节输入参数权重，以提高绕行效率，减少绕行路径。

2.5.1 模糊控制器的输入及输出 根据多次试验的经验，绕行时移动平台与障碍物的距离为50 cm左右最合适，因此预设绕行距离为50 cm。由于传感器S3、S4存在10°波束角，因此反馈相同探测距离的障碍物时，实际距离会有一定的偏差，当探测距离为50 cm时，车-障实际距离变化范围为-0.8～0.8 cm，该探测误差为绕行距离的1.6%，对绕行过程的影响较小，因此可将传感器反馈的距离作为实际车-障距离使用。绕行时定义车-障距离大于50 cm为正，反之为负。

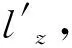
Δlz=lz-50。

(3)

车-障距离相对变化率ηz：为

(4)

式中：ηz的正负分别表示移动平台远离或靠近障碍物，数值越大反映lz变化速度越快。

将Δlz、ηz作为模糊控制器的输入，前轮转向角α作为输出，分别将三者模糊化，模糊等级均为{NB、NM、NS、ZO、PS、PM、PB}，Δlz、ηz、α的基本论域分别为[-30 cm，30 cm]、[-120%，120%]、[-40°，40°]。本研究使用Mamdani型模糊推理规则，将输入输出变量分别在[-6，+6]区间内归一化处理，得到Δlz与ηz的量化因子分别为kΔ/z=0.2、kηz=0.05，α的比例因子kα=6.67。

2.5.2 模糊控制器的自调节函数解析式 绕行模糊控制器的自调节函数解析式为：

Az=，n∈[0,1]。

(5)

式中：Az为前轮转向角模糊变量；<·>表示取整运算；n为自调整函数；ΔLz为车-障距离与绕行距离偏差的模糊变量；Hz为车-障距离相对变化率的模糊变量。

控制器工作的基本原则为：当平台绕行时，若车-障距离过近或过远，则增加距离权重，使其更快速地收敛至绕行距离；若车-障距离变化率过快，则增加距离变化率权重，使平台高效绕行的同时行驶更稳定，避免因障碍物外形变化过快导致脱离绕行或者发生碰撞。相较于普通模糊控制规则，该控制原理更加灵活，同时更适应绕行需求，提升绕行精度。根据上述原则，建立自调整函数如下：

(6)

式中：k为比例系数；W为最大偏差范围，取值为30；p为函数幂次。

如图9所示，当p<1时，函数n的值递增较快，车-障距离因素在控制决策中权重占比较大；当p>1时，车-障距离变化率权重变大，因此该权重随着p值的增加而增强。

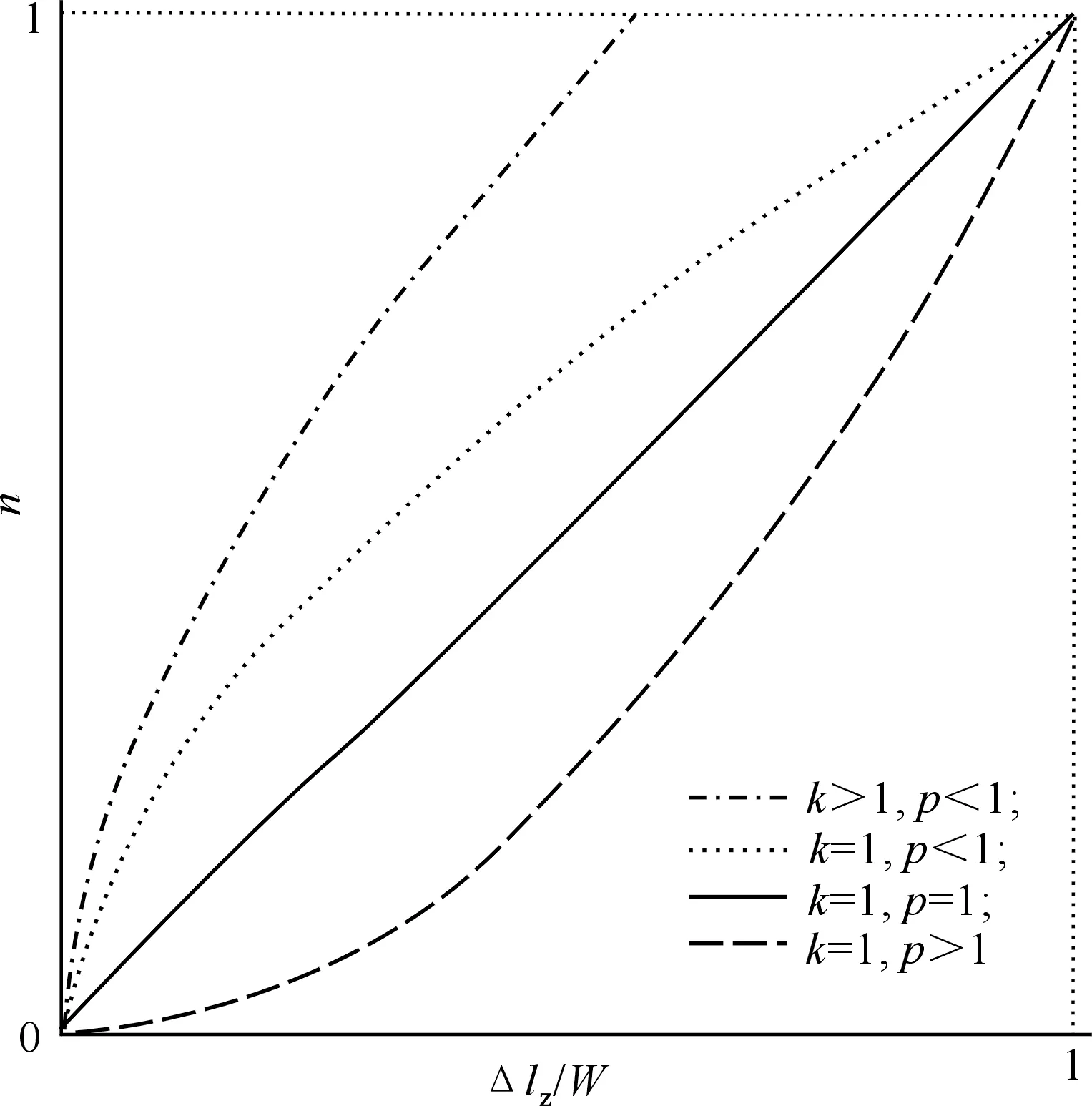
图9 模糊控制器自调节函数的变化Fig.9 Change of self-adjusting function of fuzzy controller

由于林间移动平台在林间行驶时，多为静态障碍物且障碍物边缘变化幅度较小，因此车-障距离变化率相对平缓，故应重视距离值大小，增加其比重。通过Matlab R2014a仿真，自调节函数的参数为:k=1.2，p=0.8。

3 试验验证及分析

3.1 试验设计

为验证上述避障方法的有效性，于2020年5月在浙江农林大学林学实验基地对林间移动平台进行导航避障试验，试验场地(长×宽)为12 m×3 m的林间泥地。由于移动平台在林间进行路径追踪时，较难避开林间树木和堆叠物等物体，因此本试验设计大、小2种障碍物。大障碍物为3 m×0.3 m×1.2 m(长×宽×高)的纸箱，小障碍物为直径约0.5 m的树木，障碍物均位于期望路径中央，距离导航起点4 m，跟踪路径全程12 m，车速0.5 m/s。

对试验中的数据进行如下定义：平均绕行偏差为移动平台位置与预设绕行距离偏差的均值，可反映绕行过程的偏差大小，表明算法控制的准确程度；绕行偏差范围为平台与预设绕行距离偏差的最小值和最大值，该范围对行驶的稳定性、控制的准确度均有一定参考意义；绕行标准差为绕行偏差的标准差，该值可反映绕行过程中行驶的稳定性，在狭隘的林间环境中稳定行驶可提高避障安全性和避障效率；试验总路程为移动平台从起点到终点所行驶的路程总和，理论总路程为与实际试验相同情况下理论上使用上述算法所需的总路程，将2种路程进行对比可为路径冗余、系统控制精确程度提供参考。

避障轨迹及其试验数据如图10、11及表2所示。为更好地显示避障效果，图10(a)和11(a)中的虚线矩形为平台轮廓的移动轨迹。

3.2 试验结果与分析

从图10(a)和图11(a)可见，在2种障碍物避障试验中，全程各阶段路径衔接流畅，绕行轨迹平滑且与障碍物无碰撞，避障成功。结合图10(b)和图11(b)可知，绕障过程中转向角均有明显调节，绕障轨迹均与其对应障碍物边缘相似，无轨迹突变和偏离，说明通过自调节模糊控制的方法可解决“边缘跟踪”的问题，同时实现了将改进型Bug算法应用于实际中。

从图10(b)和图11(b)可知，当期望转向角首次变为最大值时即开始避障，此时S1和S2探测到大、小障碍物的距离分别为98.0，103.0和96.0，84.0 cm，并据此算得提前避障距离分别为93.9和81.7 cm，将2组探测距离对应在图8中刚好位于绿色部分，因此提前转向的时机判断正确；避行全程无碰撞和停车等情况发生，说明避障转向角控制索引图设计合理，可解决转向响应延迟影响避障安全的问题。

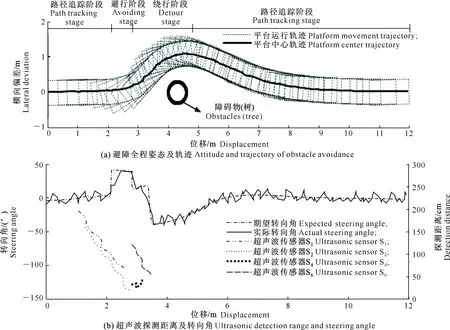
图10 林间移动平台小障碍物避障试验结果Fig.10 Obstacle avoidance test result of small obstacles on mobile platform in forest

图11 林间移动平台大障碍物避障试验结果Fig.11 Obstacle avoidance test result of large obstacles on mobile platform in forest

由表1可知，大、小障碍物绕行偏差范围分别为0.1～29.2和0.7～23.4 cm，由于林间泥地存在坑洼、石块等因素，会导致平台行驶时发生侧滑，造成偏差范围偏大。平均绕行偏差分别为-7.9和-15.2 cm，该偏差分别为车宽的11.3%和21.7%，小障碍物试验绕行偏差相对较大是因为障碍物半径较小，移动平台还未来得及调整就已结束绕障过程。2种试验的绕行标准差分别为7.5和12.4 cm，表明避障过程行驶稳定、控制精确，符合林间环境的避障要求。

由表1可知，大、小障碍物避障试验的总路程分别为1 315.5和1 223.1 cm，理论计算得到的避障路程分别为1 307.1和1 228.2 cm，差值分别为8.4和5.1 cm，试验实际值与理论值的差值分别占理论值的0.64%和0.42%，说明使用改进的Bug算法对平台控制精确且避障路径冗余小，保证了运输的高效，适用于林间环境的导航行驶。

表1 林间移动平台不同障碍物避障试验结果的统计Table 1 Statistics of obstacle avoidance test of different obstacles on forest mobile platform

4 结 论

1)用GPS定位系统获取移动平台的位置信息，在林间进行避障试验，通过改进传统Bug算法，将其导航及避障过程分为路径追踪、避行和绕行3个阶段，路径追踪阶段使用纯追踪算法；在避行阶段结合转向所需的时间，确定提前转向的位置，使用最大转向角的方式避开障碍物；在绕行阶段通过设计带自调节函数的模糊控制器，控制平台对障碍物进行“边缘跟踪”，从而实现将Bug算法应用于林间移动平台避障。

2)在大、小障碍物实际避障试验中，提前避障时机判断恰当，控制精确；平均绕行偏差分别为7.9和15.2 cm，绕行偏差最大值分别为29.2和23.4 cm，绕行标准差分别为12.4和7.5 cm，表明避障过程中移动平台行驶稳定；大、小障碍物避障试验总路程与理论总路程的差值占理论值的比例均小于1%，说明避障控制较精确，避障路径冗余较少。

3)林间环境较为复杂，平台行驶会受路面侧滑等因素影响，从而导致避障过程中绕行偏差变大，后期可对行走机构进行相应改进，以更加适应林间地面环境。