一种基于相分量的VSC-HVDC机电暂态仿真方法
2021-08-09杨欢欢徐光虎张建新邓韦斯
黄 磊,杨欢欢,徐光虎,李 鹏,张建新,邱 建,邓韦斯
(中国南方电网有限责任公司,广东 广州 510623)
0 引 言
我国电力系统的不断发展对于仿真技术提出了更高的要求[1,2]。目前对于交直流混联系统的仿真,一般集中在电磁暂态仿真方面。电磁暂态仿真精度高,能够反映换流器开关动作,但是其受制于仿真步长小,大规模的交直流混联电网仿真速度慢。而机电暂态仿真作为传统的电力系统稳定分析工具,具有计算规模大、仿真速度快的特点。随着高比例电力电子设备的引入,需要研究交直流混联系统下机电暂态的建模与仿真问题。
为了建立适用于机电暂态的仿真模型所进行的研究大致分为两个方面,一方面是对于一次系统进行改进化简,如文献[3]建立了VSC-HVDC两端系统的小信号模型,重点研究了直流输电中的稳定性问题,但并未涉及多端直流系统换流器间相互作用的分析,无法推广到大规模电网仿真中。文献[4]基于联合仿真的思想提出对将直流系统进行时变动态相量建模,对除去直流系统部分建立机电暂态模型。但是该仿真方法一方面在对故障仿真时会变的尤为复杂且在三相不对称故障仿真中误差较大,另一方面在仿真过程中需要数据接口,增加了模型的复杂性和计算量。文献[5-7]基于时变动态相量推导了模块化多电平换流器(MMC)和VSC的机电暂态仿真模型,在dq坐标系下研究了换流器在不对称故障下的仿真问题,但是上述文献所建立的机电暂态仿真模型无法对于同时含有LCC-HVDC和VSC-HVDC系统进行仿真。另一方面着重于控制系统模型的改进和化简。换流器直接控制通过控制换流器输出电压幅值和相角来达到控制目标,结构简单但电流响应慢,故在实际中应用较少。间接控制也称为“矢量控制”,在实际中应用广泛。传统的间接控制[8-11]常由外环控制和内环控制组成,电流动态响应快且具有优异的限流能力(在故障中尤为重要)。控制系统的传统模型可实现有功类控制和无功类控制的解耦,但是这种控制方式需要添加补偿来抵消耦合项和电网电压的影响,增加了复杂性且降低了鲁棒性。文献[12-15]分别提出基于反馈线性化控制思想和基于自抗扰控制技术的控制模型。
本文基于相分量,分别对一次系统和控制系统进行建模,一方面在保证精度的同时简化了直流系统与电网代数方程之间的数据接口和交换;另一方面减少了控制系统中的锁相以及dq变换环节。最后以电磁暂态仿真结果作为参考值,验证了本文方法正确性和有效性。
1 换流器模型
电磁暂态仿真中,VSC换流器的一次系统和控制系统,一般需要转换到dq0坐标系下进行建模。实际上,当三相对称时,只用考虑dq坐标系。此时,系统变量和控制量都可以看作是dq旋转坐标系下的一个复数矢量。而机电暂态仿真中,电网采用相量形式的代数方程。相量本身是一个具有旋转特性的复数矢量。因此,如果对VSC换流器的一次系统和控制系统都基于电网的相分量分别进行建模,则将会极大简化电网的代数方程与VSC换流器之间的数据接口和交换。因此,本文方法具体阐述如下:
由于在机电暂态仿真中仿真步长取值较大,一般不需要考虑换流器开关动作和内部特性,因此,换流器多采用只考虑外部特性的受控源模型。当不考虑内部特性时,两电平的VSC换流器和MMC换流器的一次系统和控制系统是一致的,本文进行统一建模。
1.1 交流侧
图1所示为与交流电网相联的换流器交流侧模型。其中Rc和Lc为VSC系统中变压器及线路的等效电阻和电感,Bc为滤波电容(MMC时可不考虑)。

图1 换流器交流侧等效电路Fig.1 Equivalent circuit on the AC side of the converter
换流器交流侧模型可等效为受控电压源,列写出交流侧系统模型方程如下。考虑到机电暂态特性,方程中各物理量可采用相分量表示,为书写方便省去各物理相分量里的时间变量。考虑到三相的相似性,下面用A相来描述其物理特性,在方程中省去A相下标,后面若无特殊说明各物理量均指A相,A相的交流侧相分量动态方程如式(1)所示:
(1)
式中:Ut为PCC点相电压;Uc为换流器出口电压;UtRe、UtIm、UcRe、UcIm、ItRe、ItIm分别为Ut、Uc、It的实部和虚部分量。需要指出的是,各电气量的实部和虚部是以PCC点Ut相位作为参考相位的结果。
1.2 直流侧
换流器直流侧模型如下,在直流侧并联电容Cconv,如图2所示。

图2 换流器直流侧等效电路Fig.2 Equivalent circuit on the DC side of the converter
等效为受控电流源是因为交流侧三相电流在开关的调制作用下成为上下桥臂电流,且三相上下桥臂电流合成的正负极电流大小相等,方向相反。等效为并联电容表示换流器在直流侧通过集中电容连接正负极(如VSC),对于通过分散电容连接正负极(如MMC),需通过一定的关系式对其分散电容等效。等效原则[16,17]为对于直流侧电压变化所引起分散电容和等效集中电容中能量的变化应该是相同的。由此可以得到等效集中电容和分散电容的关系:
(2)
(3)
式中:C0为MMC桥臂上每个子模块电容;N为每一桥臂子模块数量;Cconv为等效模型直流侧的等效集中电容。
因此两种结构的换流器均可用图2所示的直流侧模型来表示。
根据能量守恒关系,在忽略损耗条件下交直流两侧注入功率相等,可求得直流侧电流。
(4)
由式(5)Pd=Pc可得
(5)
式中:Pc为换流器交流侧三相有功功率;Pd为直流侧功率;Udc为直流侧正负极母线间电压;
2 控制系统
结合以相分量表示各物理量的换流器一次系统模型,对经典双闭环控制系统进行改进和简化,得到适用于本文换流器模型的控制系统,在设计控制系统是各物理量采用单相值。
2.1 内环设计
由换流器一次系统方程公式(1)可知,实部和虚部电流分别受到耦合项和电网电压的影响。类似于传统电磁暂态仿真中的内环设计,可按图3中所示的内环控制方式消除上述影响。

图3 含内环控制的换流器系统结构图Fig.3 Converter system structure drawing with inner ring control
进一步分析图3所示的内环控制系统,结合VSC换流器的物理系统,可以将图3转换成图4所示的系统结构,实部、虚部电流实现了独立解耦控制。

图4 简化后的含内环控制的换流器系统结构图Fig.4 Structure diagram of a simplified converter system with an inner ring control
在设计VSC的双环控制器时,一般采取的原则是:从外环、内环到开关的截止频率依次按十分之一变化。因此,在机电暂态仿真中,由于仿真步长相对于电磁暂态仿真要大得多,可认为电流控制环节的响应时间相对于仿真步长来说足够快,因此,可保留外环控制,而将内环的传递函数看做为1,此时其电流控制环节的结构简化为图5所示。

图5 基于相分量模型的含内环控制的换流器系统结构图Fig.5 Structure diagram of converter system with inner ring control based on phase components
2.2 外环设计
由于采取的是相分量的一次系统建模,因此VSC机电暂态模型的外环控制器可类似于VSC的电磁暂态仿真模型。根据外环输入控制量的性质,同样可分为有功功率类控制(有功功率、直流电压)和无功功率类控制(无功功率、交流电压)。与电磁暂态仿真不同的是,由于相分量已经提供了相位信息,因此在VSC的机电暂态的控制系统中,可以不包括锁相,而是用一个简单的移相环节来代替。通过移相,将PCC点的Ut的相位作为参考相位,从而实现控制量实部和虚部的解耦,此时外环控制器结构如图6所示。
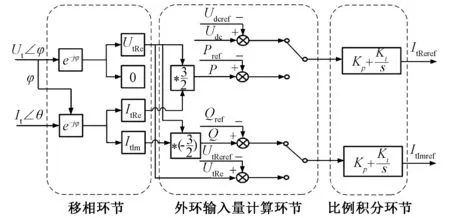
图6 外环控制系统图Fig.6 Outer ring control system diagram
当换流器一次系统模型各物理量用相分量表示时,对应的机电暂态控制系统有如下特点:①对传统电磁暂态双闭环控制系统进行改进,得到各控制量也为相量形式的控制系统模型;②基于内环的快速响应对内环控制部分进行化简,可以认为内环控制传递函数为1;③加入移相环节,实现实部和虚部的解耦。
结合本文一次侧模型和控制模型,给出基于相分量的VSC换流器机电暂态模型,如图7所示。

图7 VSC换流器机电暂态模型Fig.7 Electromechanical transient model of VSC
其中值得说明的是,在MMC中可以没有图7中PCC处的滤波器。
3 直流线路模型
由于机电暂态的仿真步长较大,因此直流侧线路模型可直接采用PI型电路模型,如图8所示。其中,Rl、L1、Cl分别取线路Req、Leq、Ceq。

图8 直流侧线路模型Fig.8 DC side line model
建立线路模型方程,并将方程中物理量的实部和虚部分别列写,串联支路方程和对地电容支路方程(以i节点为例)如下:
(6)
(7)
对上述方程进行差分化,差分化后的方程为
(8)
(9)
建模时将各换流器直流侧电容并入直流网络,其微分与差分方程分别为
(10)
(11)
4 算例分析
4.1 算例参数
为验证模型的有效性,以图9所示的二端VSC直流输电系统为仿真对象,仿真对象的具体参数如表1所示。在仿真过程中采用定直流电压和定无功功率控制,以不同工况下电磁暂态仿真结果作为参考值来验证模型的有效性。

图9 二端VSC直流输电系统Fig.9 Two-terminal VSC HVDC system

表1 仿真对象参数Tab.1 Parameters of the simulation object
其中,K为变压器变比;Xt为变压器等效阻抗;Xc为换流器一次系统等效阻抗;Bc为滤波器电容;Cconv为直流侧换流器等效集中电容;SB为换流器额定容量;UdB为直流侧额定电压;R为线路等效电阻;L为线路等效电感;C/2为线路等效对地电容。
4.2 不同工况下的仿真结果
4.2.1 有功功率阶跃响应工况
有功功率阶跃响应工况设置如下:在0.1 s时整流端交流侧有功功率向下跌落,在1.1 s时有功功率向上阶跃。
整流侧和逆变侧有功功率P、无功功率Q和整流换流器直流侧电压Ud变化情况如由图10、图11和图12所示:
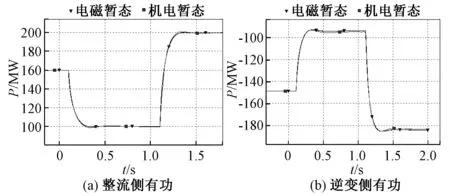
图10 有功功率变化情况Fig.10 Variation of active power
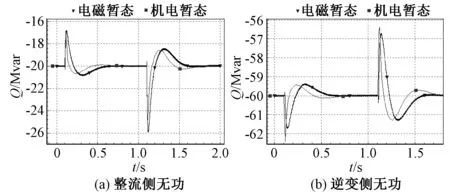
图11 无功功率变化情况Fig.11 Variation of reactive power

图12 整流换流器直流侧电压变化情况Fig.12 Voltage variation at DC side of rectifier
由图10、图11和图12可知,在有功功率发生阶跃响应工况下:一方面,两端有功功率、无功功率和整流器直流侧电压的机电暂态仿真结果与电磁暂态仿真结果大体一致;另一方面,定直流电压控制和定无功功率控制基本达到要求,具体表现为在扰动后整流器直流电压与直流电压参考值存在一个可接受的偏离,这种偏离是由于扰动前后有功功率的不同导致。无功功率在扰动后则与无功功率参考值吻合较好。综上,在此种工况下,本文模型是有效的。
4.2.2 三相短路故障工况
三相短路故障工况设置如下:在0.1 s时整流端交流侧发生三相短路故障,在0.2 s时恢复正常。
整流侧和逆变侧有功功率P、无功功率Q、整流换流器控制系统中实轴虚轴参考电流ItReref、ItImref和整流换流器直流侧电压Ud变化情况如如由图13、图14、图15和图16所示。
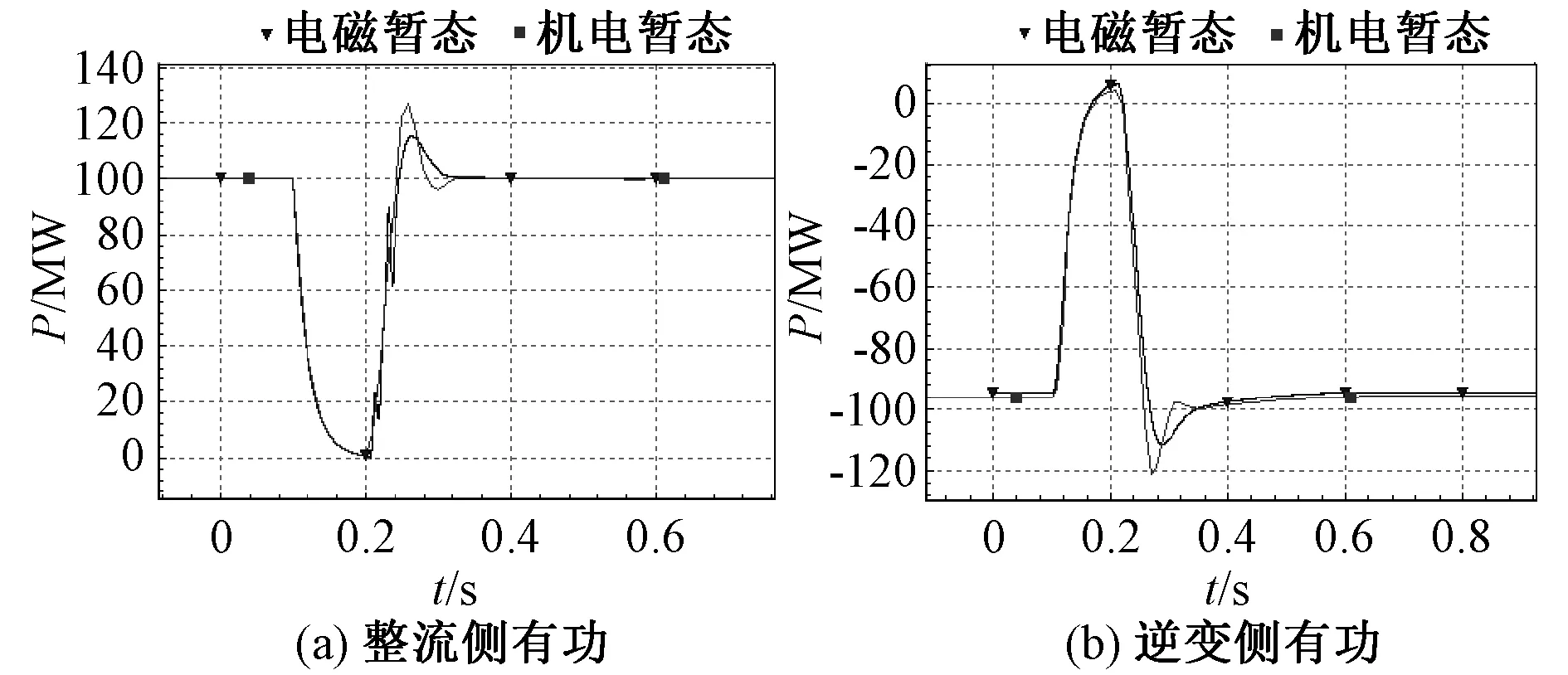
图13 有功功率变化情况Fig.13 Variation of active power
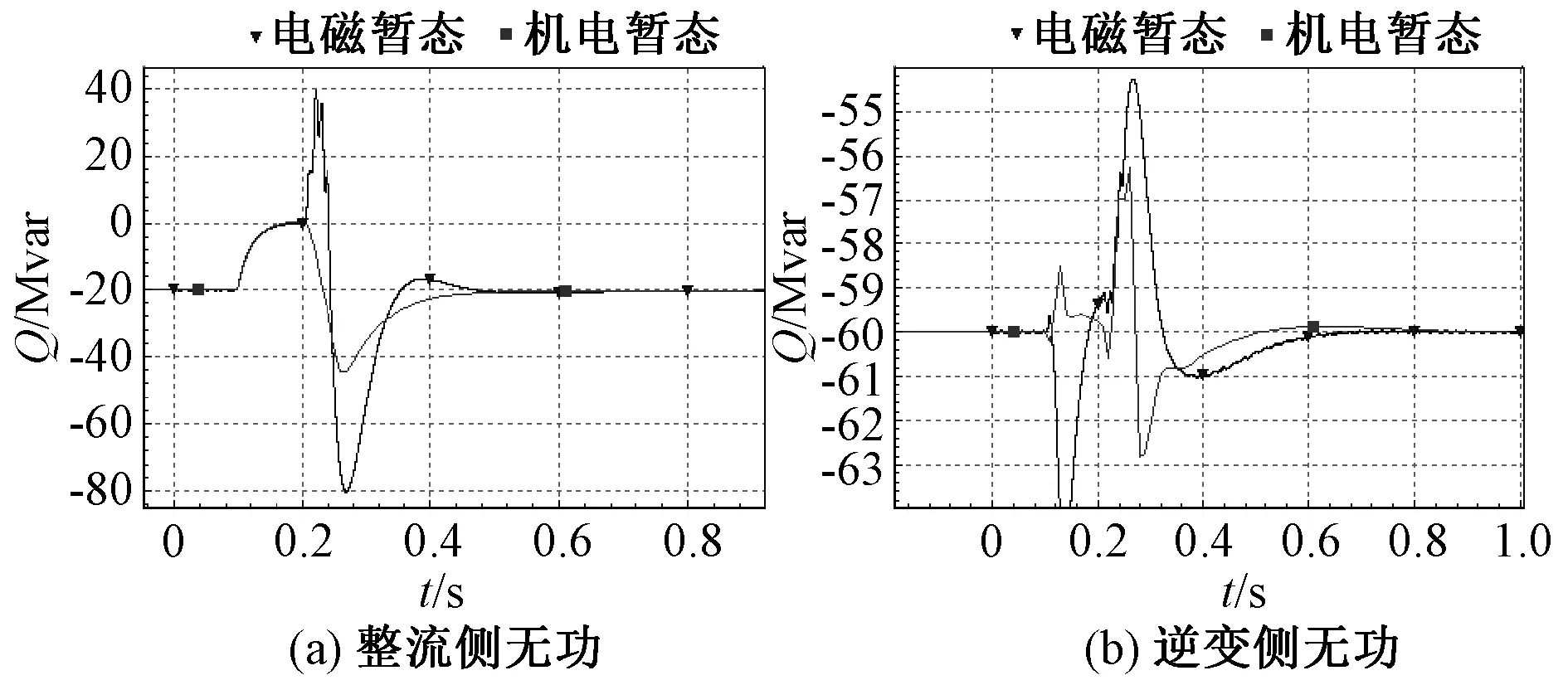
图14 无功功率变化情况Fig.14 Variation of reactive power
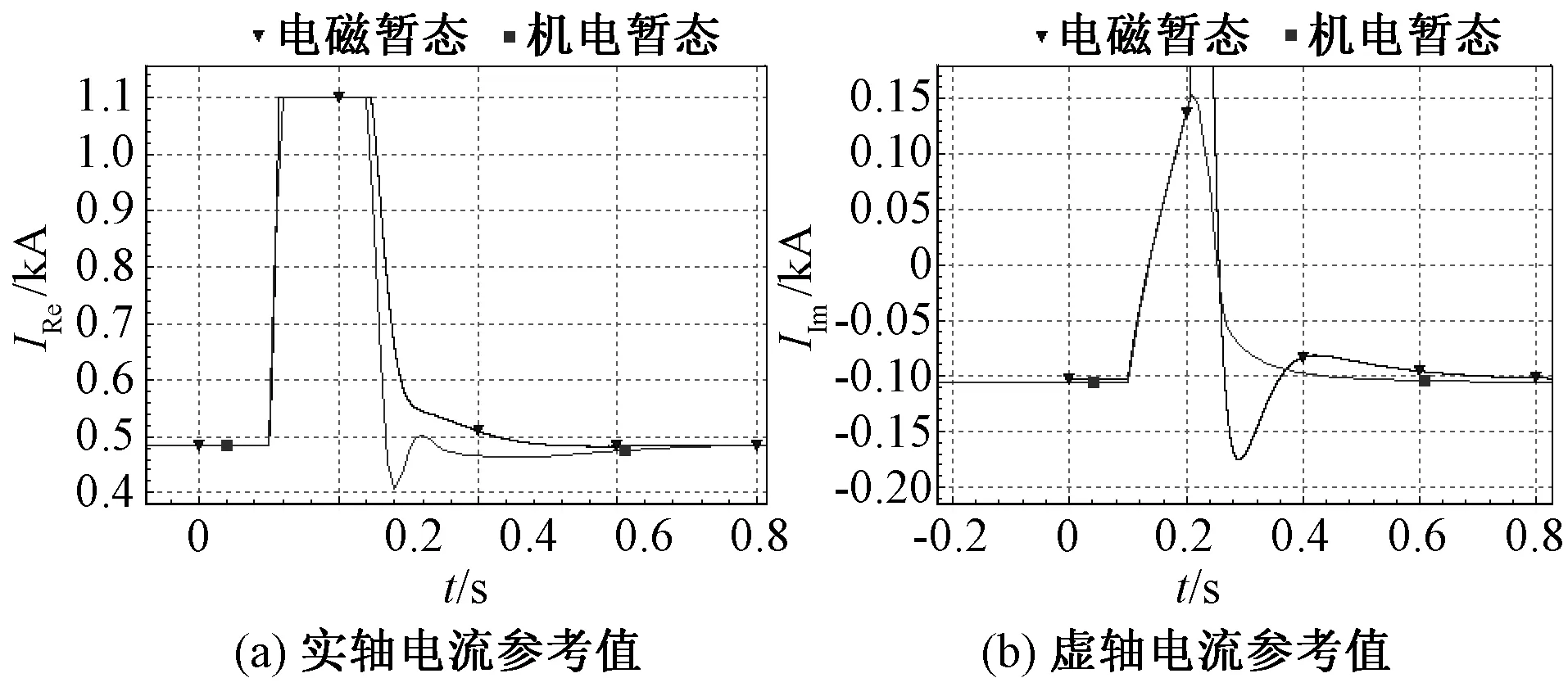
图15 参考电流变化情况Fig.15 Reference current variation
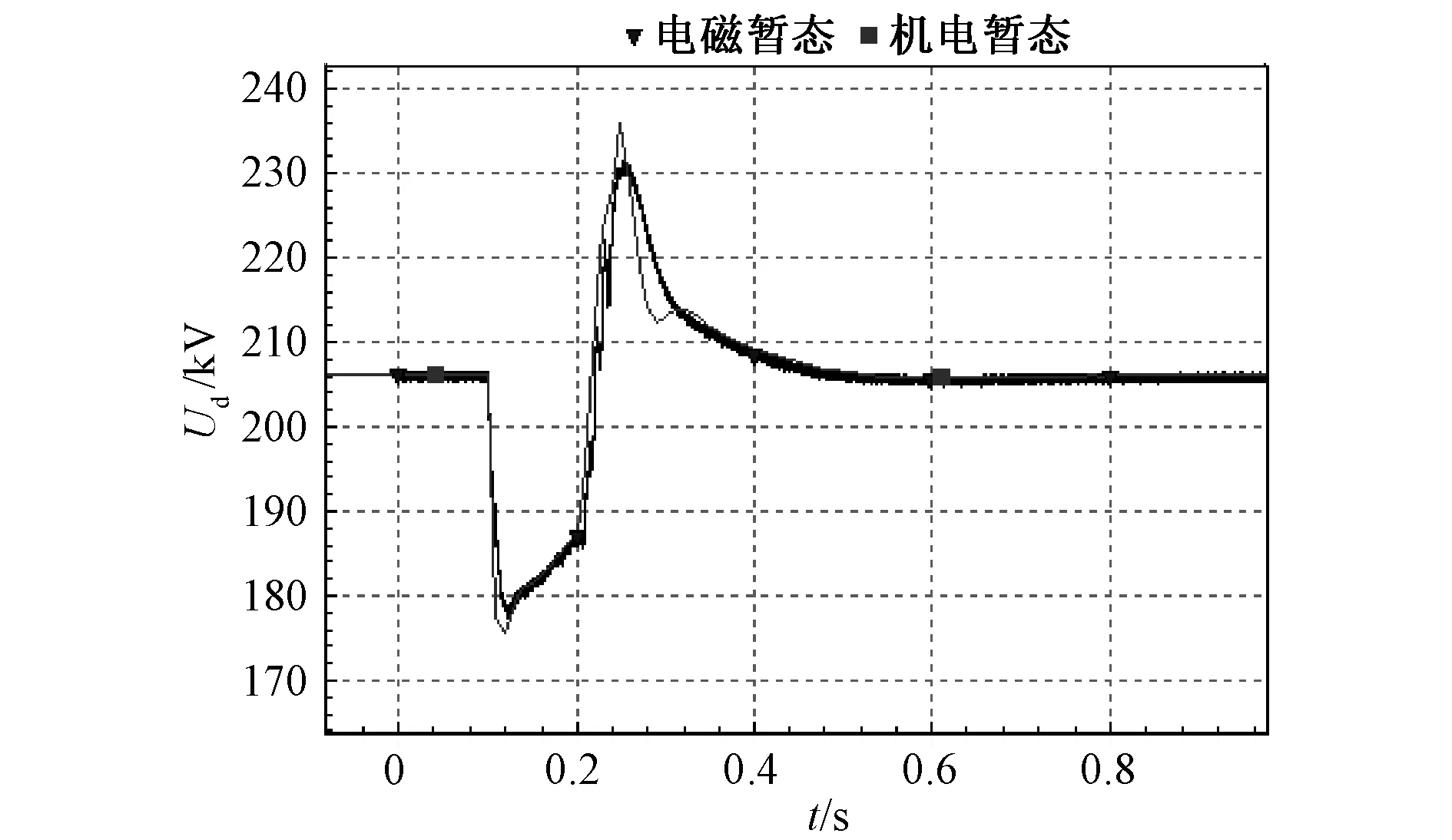
图16 整流换流器直流侧电压变化情况Fig.16 Voltage variation at DC side of rectifier
由图13-16可知,在三相短路故障工况下,各物理量机电暂态仿真结果与电磁暂态仿真结果拟合较好,进一步验证了模型有效性。此外,由图15可知,实轴电流参考和虚轴电流参考值与电磁暂态仿真中d轴和q轴电流参考值基本一致,这表明了本文中外环控制环节模型的有效性,即移相环节的引入是有效的。
5 结 论
本文建立了基于相分量的VSC-HVDC的机电暂态仿真模型,充分考虑了机电暂态的特点。一方面基于相分量的方法可以简化数据接口和交换;另一方面控制系统建模过程中对内环控制的简化处理以及移相环节的引入,极大的简化和降低了VSC机电暂态模型的复杂度。最后通过算例分析表明:所建立的机电暂态模型是有效的,能够正确仿真正常和故障条件下的多种工况。
