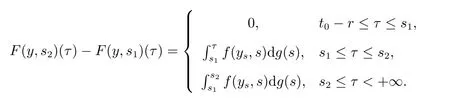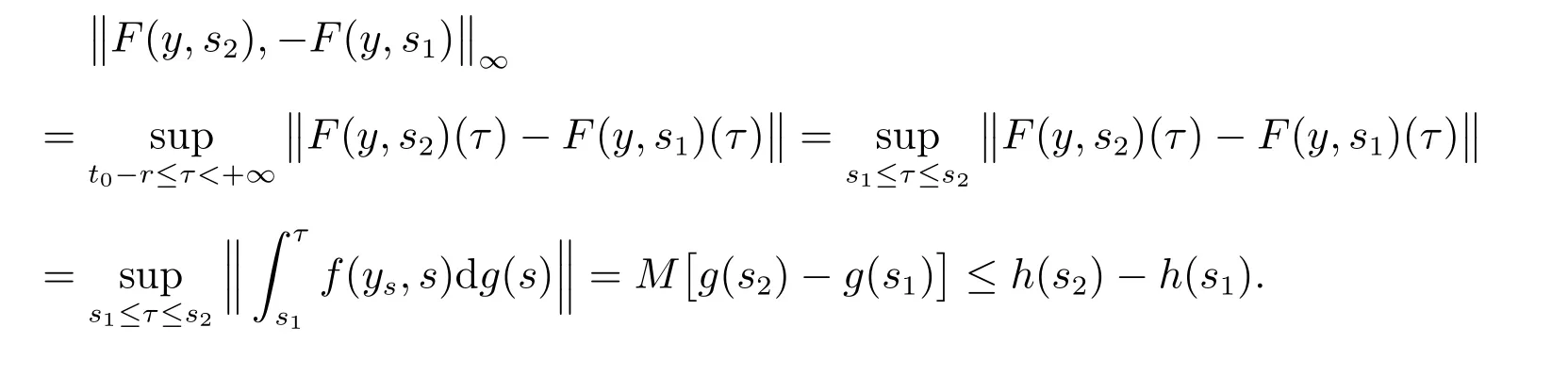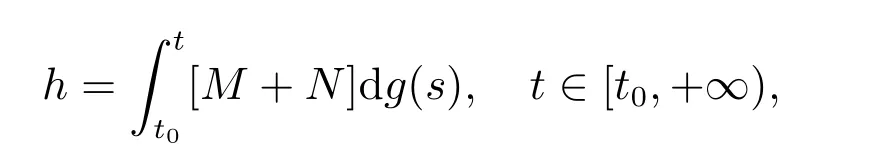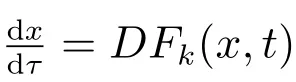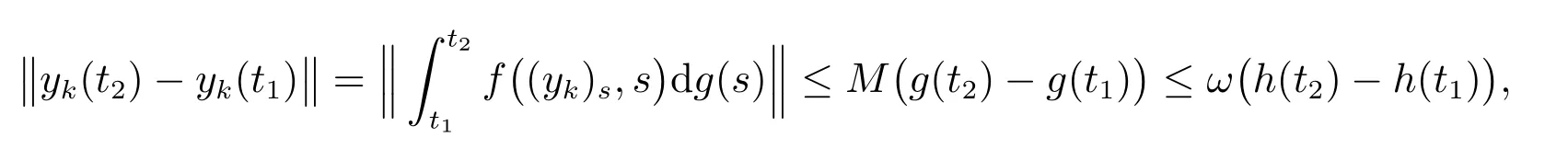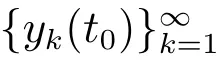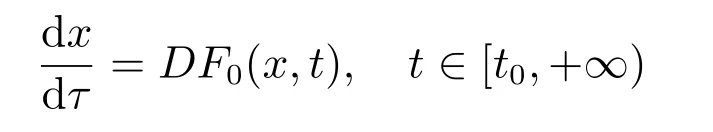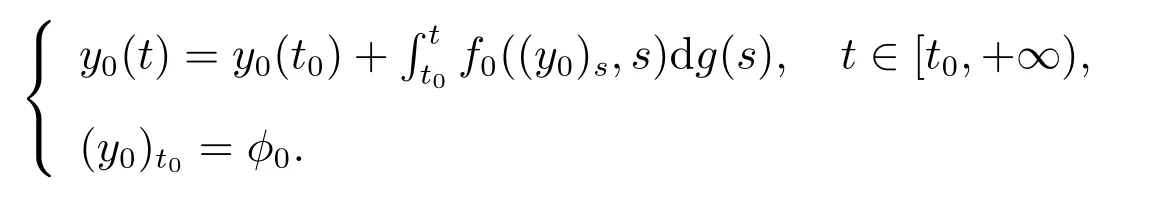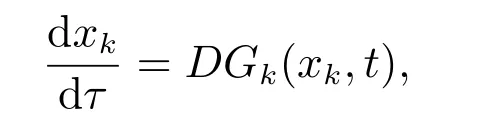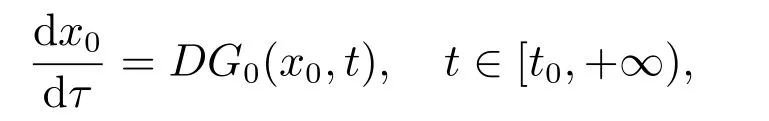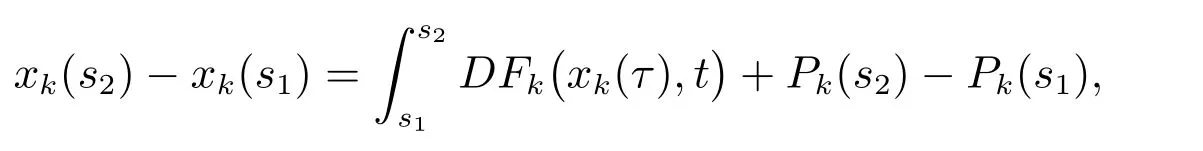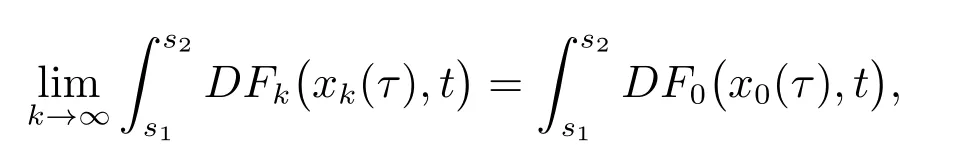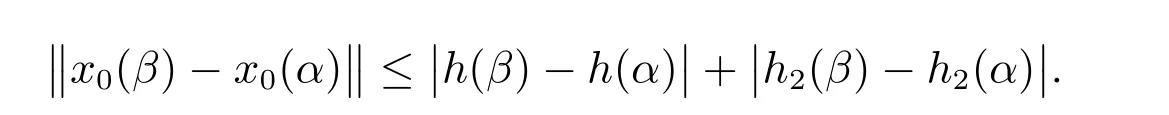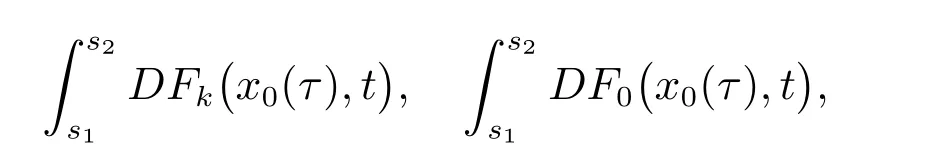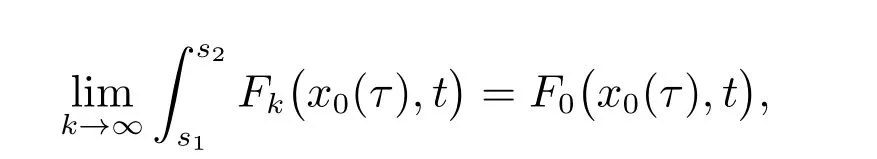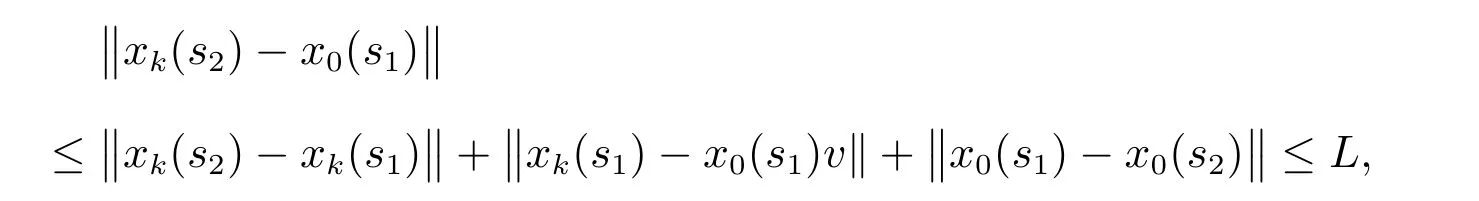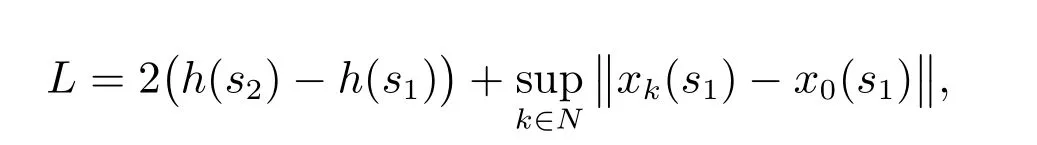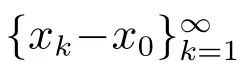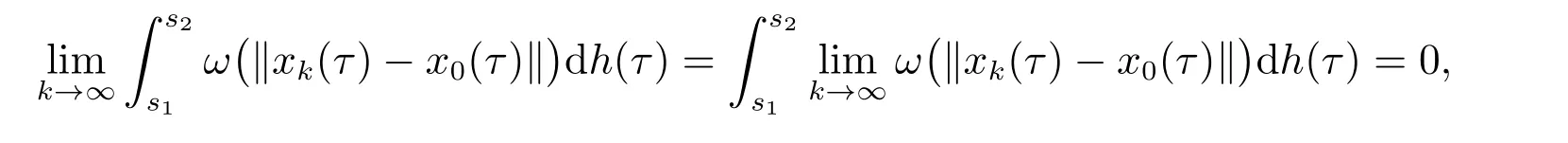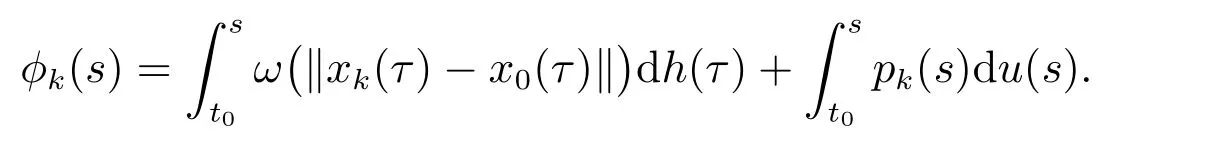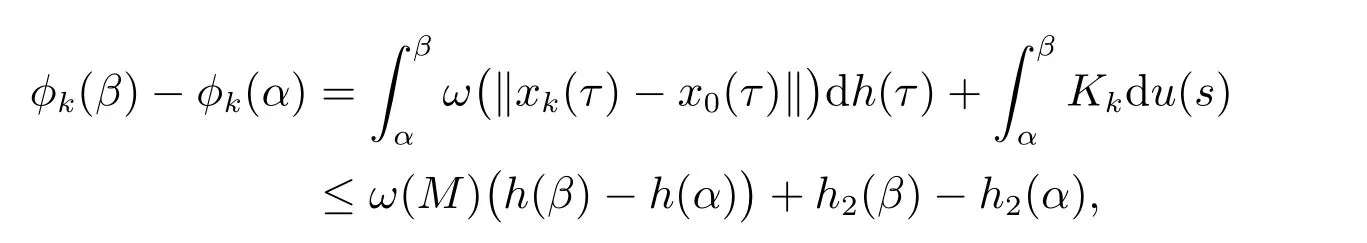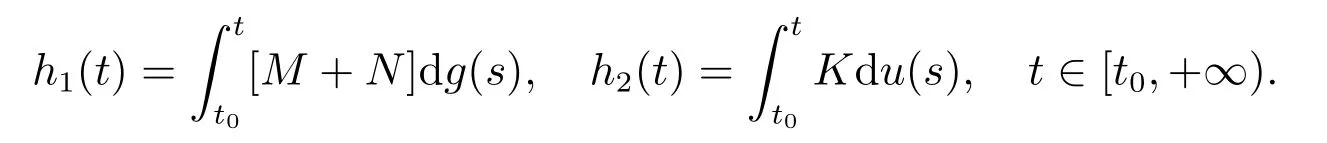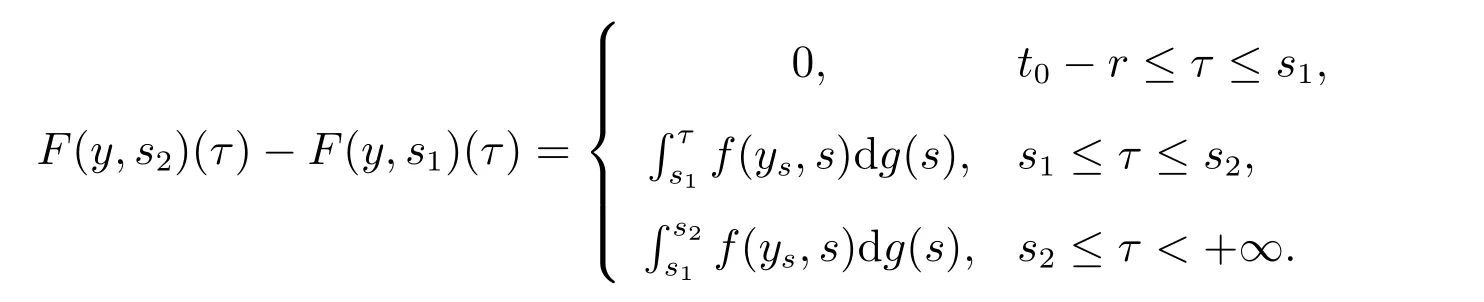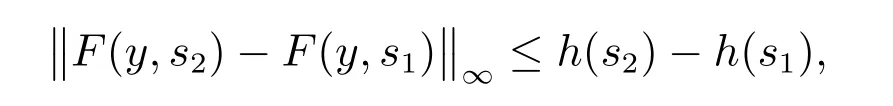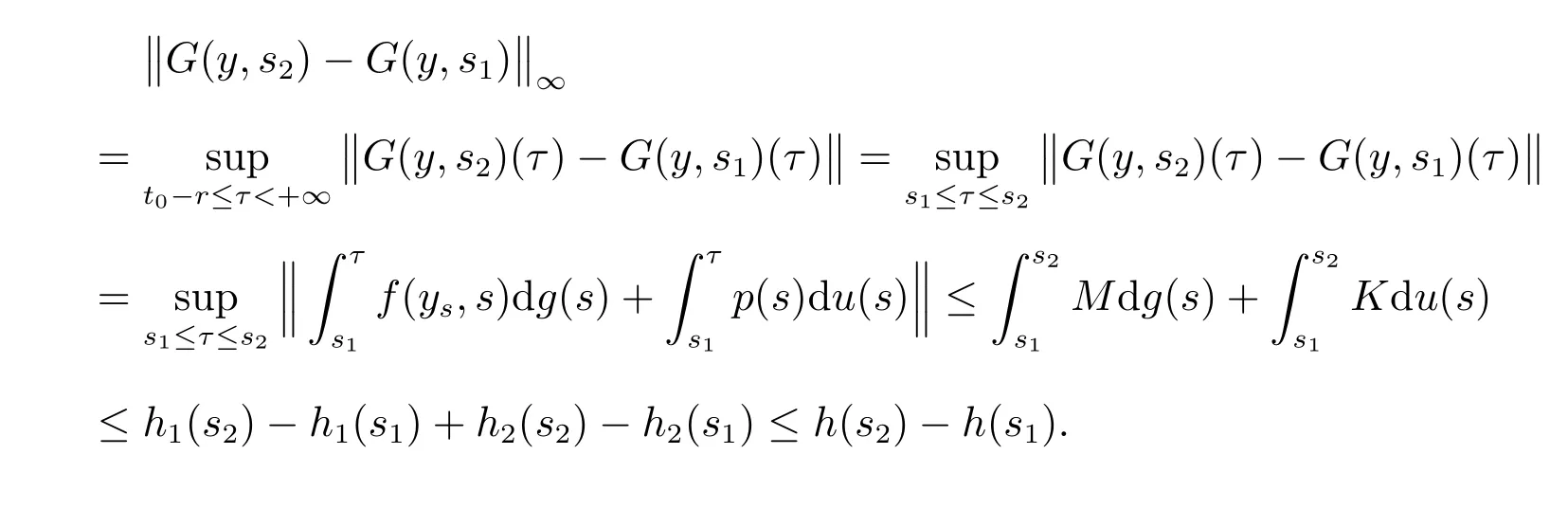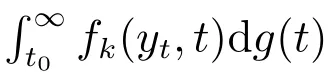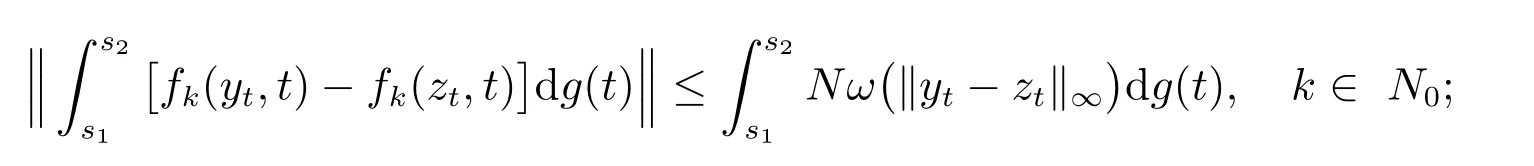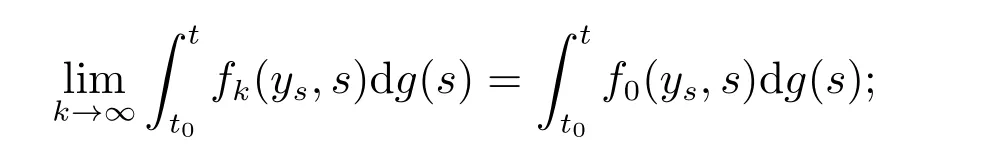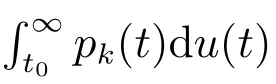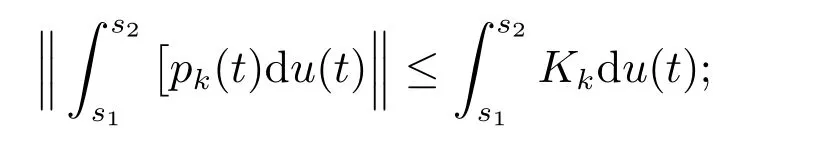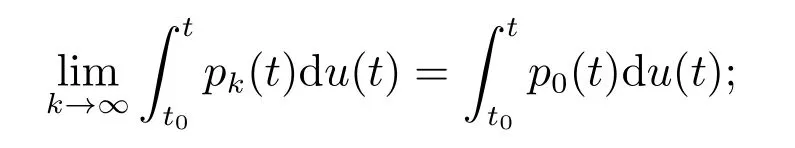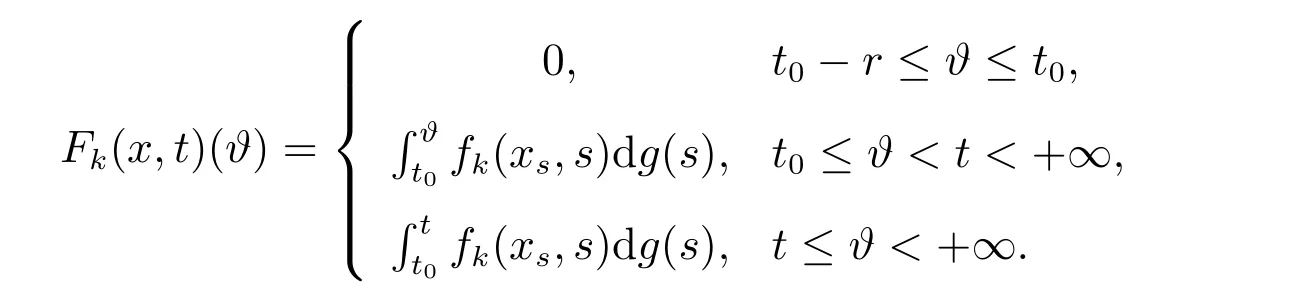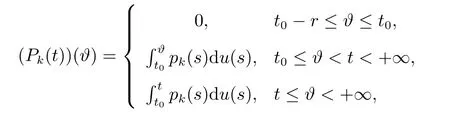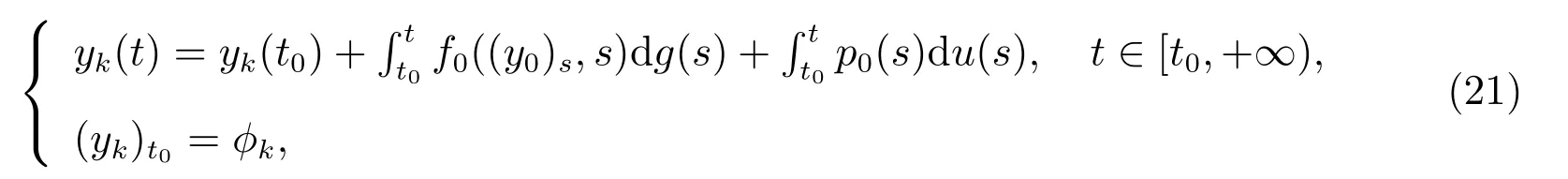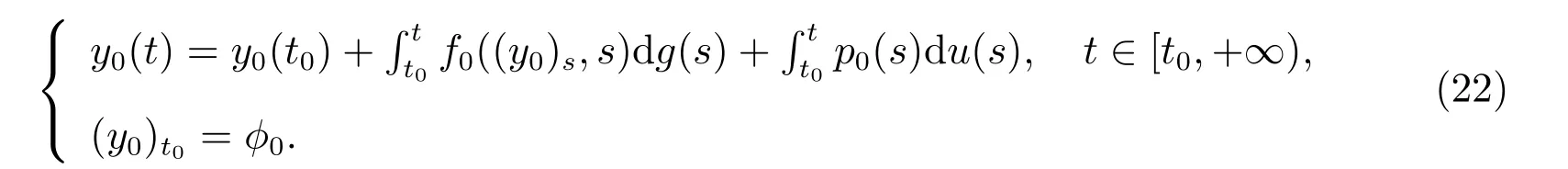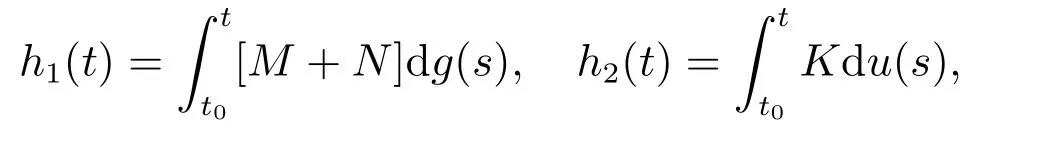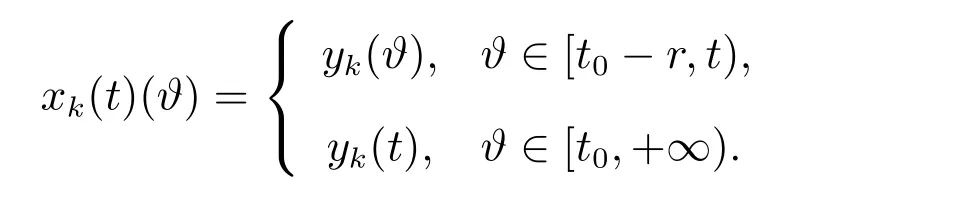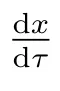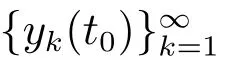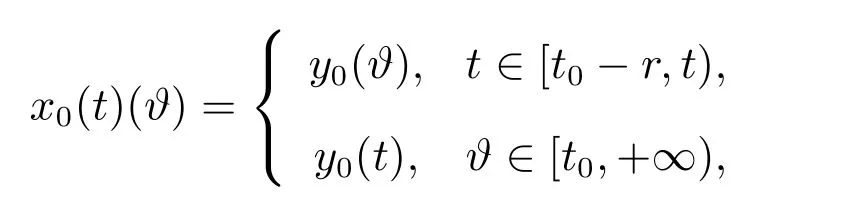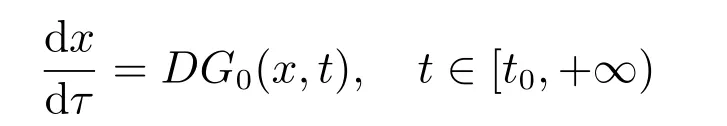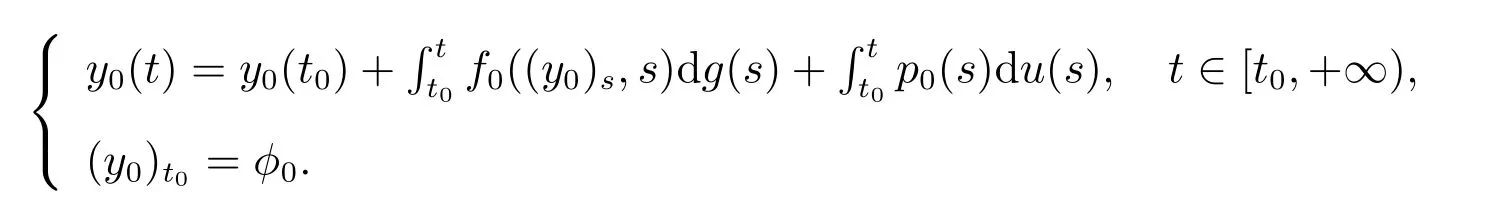滞后型测度泛函微分方程解对参数的连续依赖性
2021-08-08李宝麟杨万秀
李宝麟, 杨万秀
(西北师范大学数学与统计学院,兰州 7 30070)
1 引言
当常微分方程˙x=f(x,t)所描述的系统受到扰动时,对受到扰动的系统导出的常微分方程的形式为
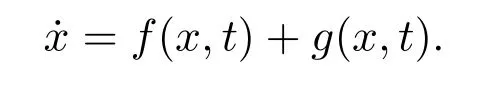
如果扰动项是连续可积的,那么扰动后的系统仍为常微分方程系统,它的解为连续的,若扰动项为脉冲型的,则扰动后的系统的状态就不随时间连续变化,而是呈现一种瞬时性态,对这种数学模型的研究导出另一种方程即测度微分方程,其一般形式为

在文献[1]中,Kurzweil在1957年首次提出了广义常微分方程理论.Schwabik在文献[2]中研究了广义常微分方程解对参数的连续依赖性,并在一定条件下建立了测度微分方程与广义常微分方程的等价关系.在文献[3]中介绍了Banach空间中广义线性微分方程解对参数的连续依赖性.文献[4,5]建立了在一定条件下测度泛函微分方程与广义常微分方程的等价关系,并对解的存在唯一性及解关于初值条件的可微性,以及时间尺度上的泛函动力方程的周期平均化做了系统研究.文献[6]证明了在抽象的Banach空间中广义常微分方程解的存在性和唯一性,并证明了广义常微分方程的解关于初值和参数的连续依赖性.
考虑滞后型测度泛函微分方程

和它所描述的系统受到扰动后的滞后型测度泛函微分方程
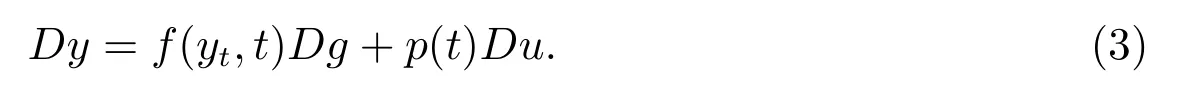
其中方程(2)等价于积分方程
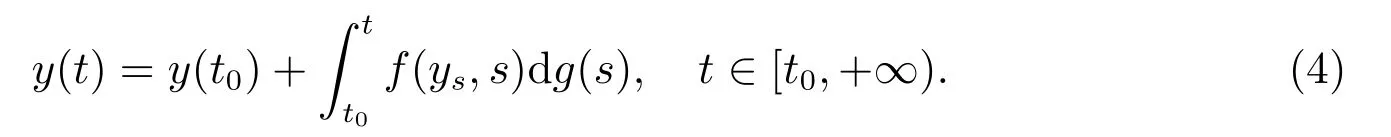
方程(3)等价于积分方程
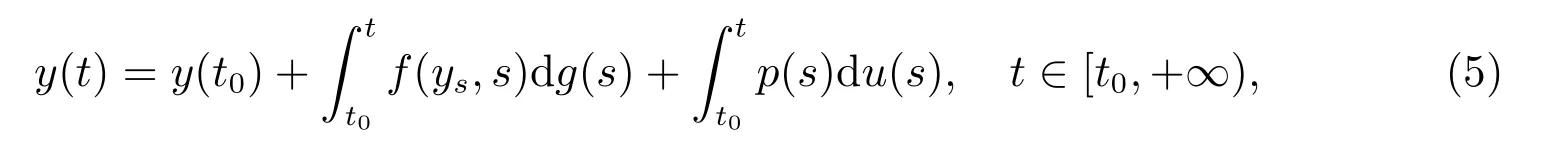
且方程(4)和方程(5)右端的积分是关于不减函数g,u:[t0,+∞)→R的Kurzweil-Stieltjes积分.
文献[7]建立了在一定条件下滞后型测度泛函微分方程与广义常微分方程的等价关系,研究了滞后型测度泛函微分方程的积分稳定性,其中Dy,Dg,Du分别是y,g,u的分布导数,函数f:T×[t0,+∞)→Rn,g,u:[t0,+∞)→R,y:[t0−r,+∞)→Rn,yt(θ)=y(t+θ),θ∈[−r,0],r>0,p:[t0,+∞)→Rn,且T={yt:y∈O,t∈[t0,+∞)}⊂G([−r,0],Rn),O⊂G([t0−r,+∞),Rn)是开集,G([t0−r,+∞),Rn)表示[t0−r,+∞)到Rn的所有有界正则函数全体,其中的范数为

而且f与p满足如下条件:
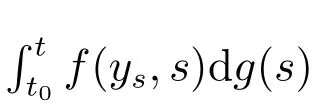
(H2): 对任意的y∈O,s1,s2∈[t0,+∞),存在一个常数M>0,使得
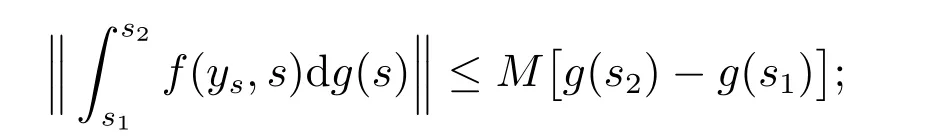
(H3): 对任意的y,z∈O,s1,s2∈[t0,+∞),存在一个常数N>0,使得
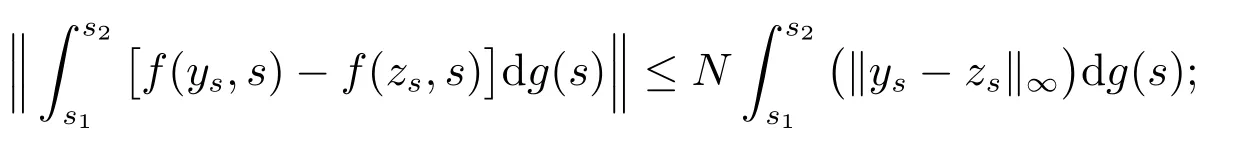
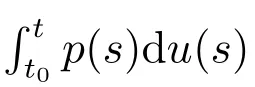
(H5): 对任意的t∈[t0,+∞),s1,s2∈[t0,+∞),存在一个常数K>0,使得
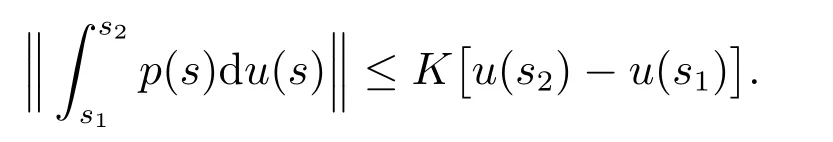
本文研究方程(2)和(3)在满足(H1)–(H5)的条件下解对参数的连续依赖性.
本文主要包括三部分:第2部分重点介绍文中所要用到的基本概念及已有结果;第3部分给出滞后型测度泛函微分方程(2)和(3)解对参数的连续依赖性定理.
2 预备知识
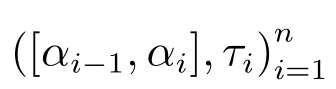
定义2[2]函数U:[a,b]×[a,b]→Rn在区间[a,b]上是Henstock-Kurzweil可积的,如果存在I∈Rn,使得对任意的ε>0,存在正值函数δ(t):[a,b]→(0,+∞),使得对[a,b]的任何δ-精细分划D=(τj,[αi−1,αi]),j=1,2,···,k,其中τj∈[αi−1,αi]⊂[τj−δ(τj),τj+δ(τj)],有
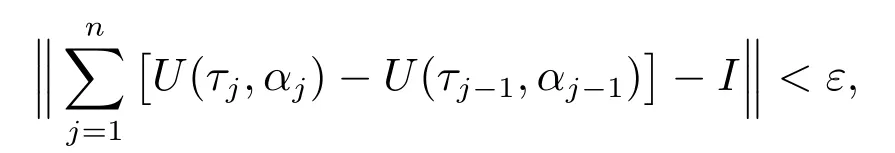
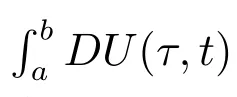
特别地,当f:[a,b]→Rn,且g:[a,b]→R,U(τ,t)=f(τ)g(t)时,
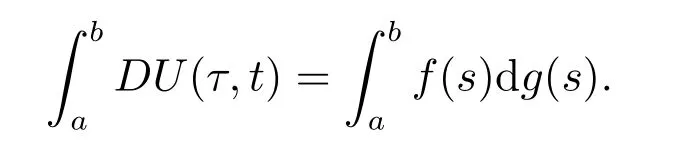
设F:Ω→Rn,Ω=O×[t0,+∞).
定义3[2]设函数F:Ω→Rn,如果x:[α,β]→Rn是广义常微分方程

在区间[α,β]⊂[t0,+∞)上的解,是指对所有的t∈[α,β],(x(t),t)∈Ω,任意的s1,s2∈[α,β],有
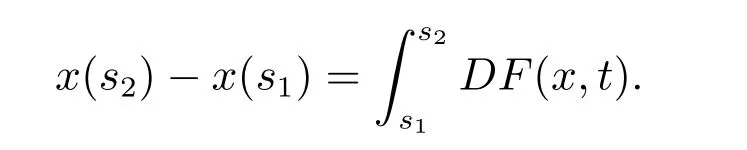
定义4[1]设函数h:[t0,+∞)是不减左连续的,ω:[0,+∞)→[0,+∞)是连续单调递增函数且ω(0)=0,函数F:Ω→Rn,属于函数族F(Ω,h,ω)是指F满足以下条件,对任意的(x,s1),(x,s2)∈Ω,有
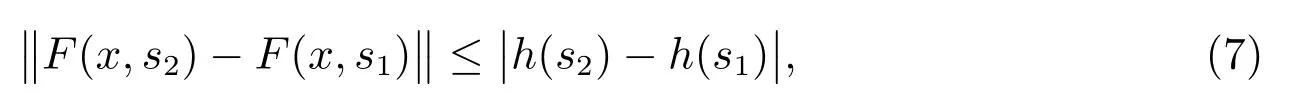
对任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω,有
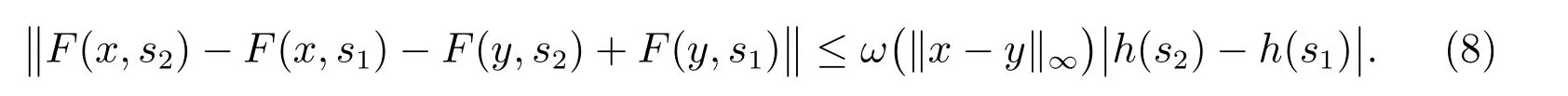
引理1[7]以下条件是等价的:
1)A是集合且A⊂G([α,β],Rn)是相对紧集;
2) 对每个x∈A,t1,t2∈[α,β],集合{x(α);x∈A}是有界的且存在连续增函数ω:[0,∞)→[0,∞),ω(0)=0,及不减函数h:[α,β]→R,使得
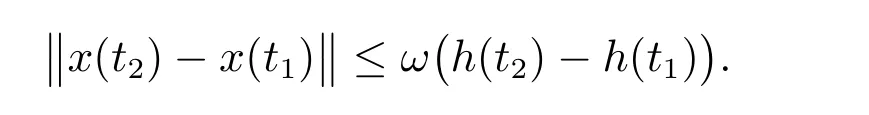
引理2[6]设X是一个Banach空间,O⊂X是开集,G=O×[a,b],h是不减的左连续函数,ω连续增加函数,函数列Fk:O×[a,b]→X,对每个k∈N0,(x,t)∈G,Fk∈F(G,h,ω),有
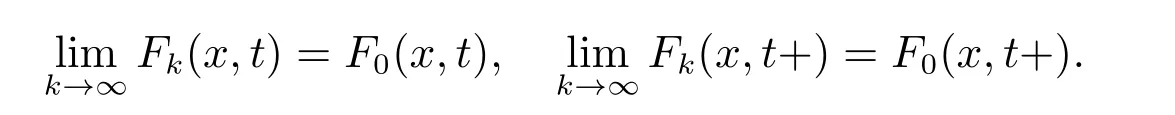
若存在一个序列函数xk:[t0,+∞)→O,k∈N0,使
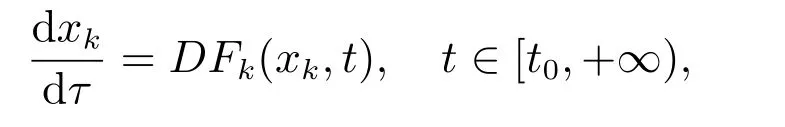
且对每个t∈[t0,+∞),有limk→∞xk(t)=x0(t),则有
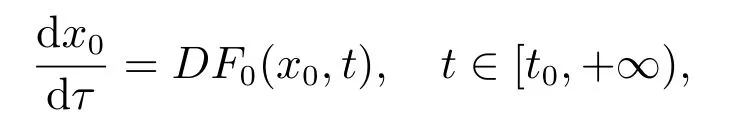
注1[7]若O是G([t0,+∞))的子集,称O具有延拓性质,是指对于每个y∈O,¯t∈[t0,+∞),都有¯y∈O,其中函数¯y定义如下
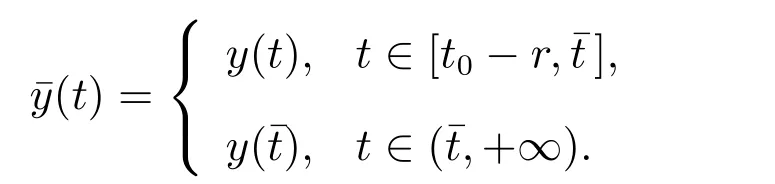
引理3[7]设f:T×[t0,+∞)→Rn满足(H1)–(H3).函数g:[t0,+∞)→R为不减的函数,对于y∈O,t∈[t0,+∞),定义如下函数
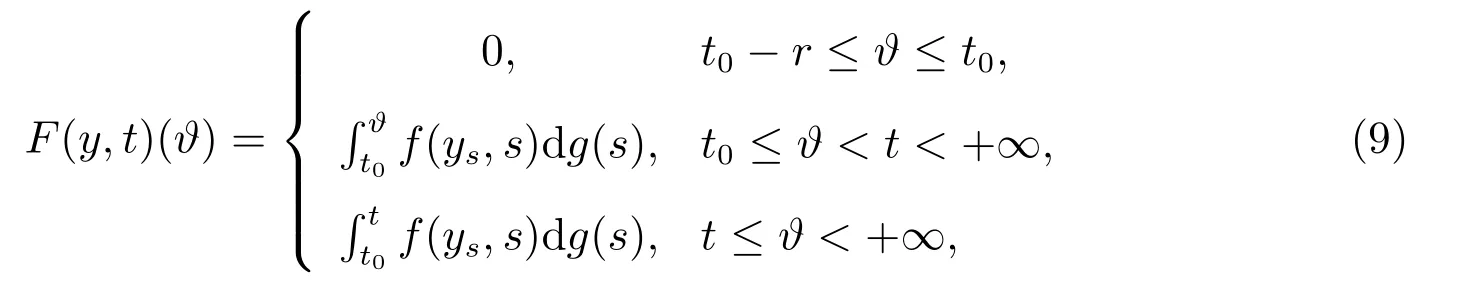
则F∈F(Ω,h),其中F:Ω→G([t0−r,+∞),Rn).
引理4[7]设O⊂G([t0−r,+∞),Rn)是开集,且t∈[t0,+∞)时具有延拓性质,T={yt:y∈O,t∈[t0,+∞)},φ∈T,g:[t0,+∞)→R是不减函数,f:T×[t0,+∞)→Rn满足(H1)–(H3),F:O×[t0,+∞)→G([t0−r,+∞),Rn)由公式(9)给定.
(i) 假设对于任意的y∈O,t∈[t0,+∞),如果y:[t0−r,+∞)→O是滞后型测度泛函微分方程
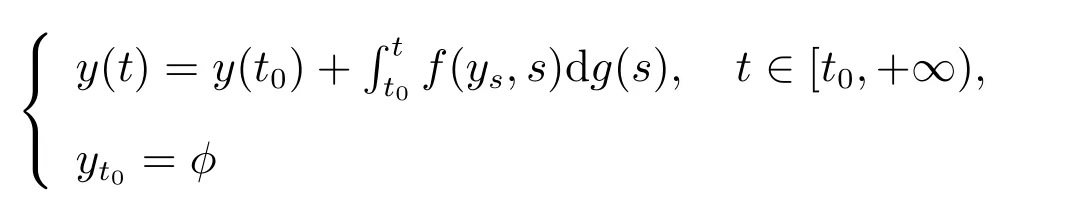
的解.
对任意的t∈[t0−r,+∞),有
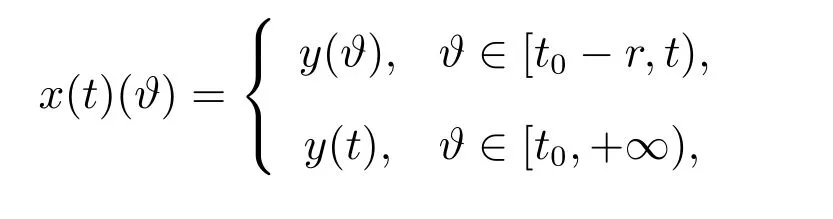

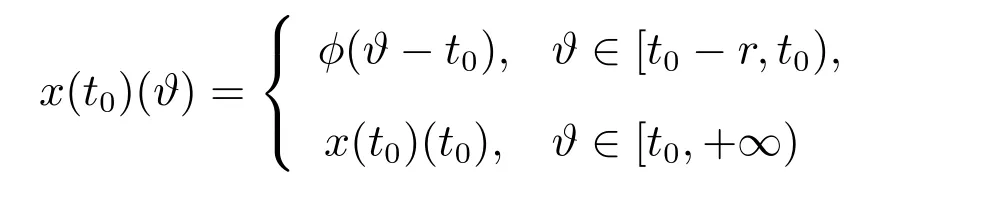
的解,其中F由(9)式给定.
(ii) 相反地,F由(9)式给定,如果x:[t0,+∞)→O是广义常微分方程
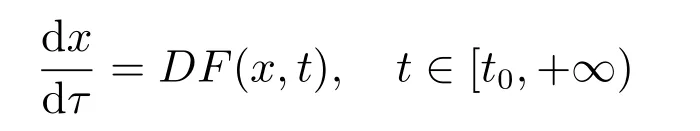
的解,且满足初值条件
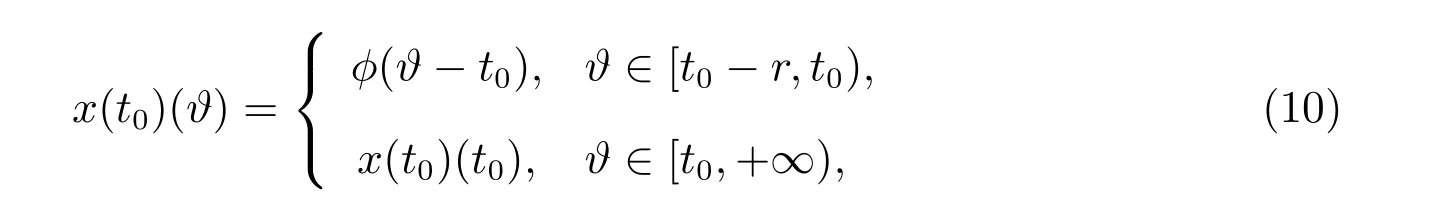
则函数y:[t0−r,+∞)→O是滞后型测度泛函微分方程
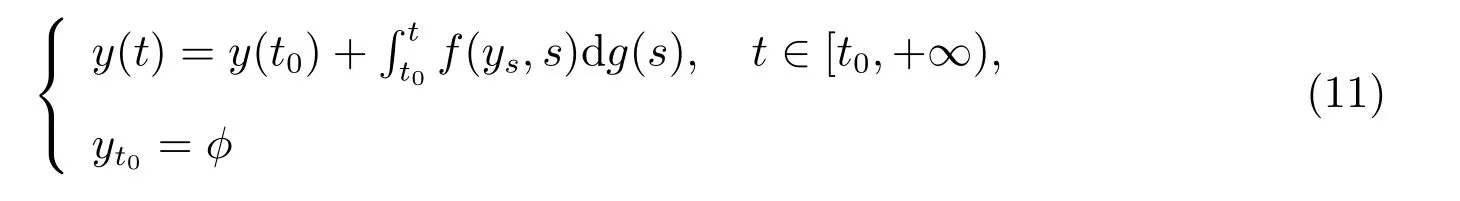
在初值条件
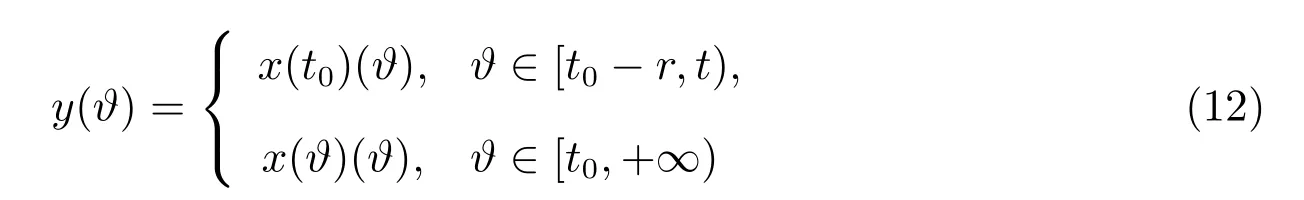
的解.
引理5[7]设f:T×[t0,+∞)→Rn满足(H1)–(H3),且p:[t0,+∞)→Rn满足(H4),(H5),函数g,u:[t0,+∞)→R为不减的,对于y∈O,t∈[t0,+∞),定义如下函数
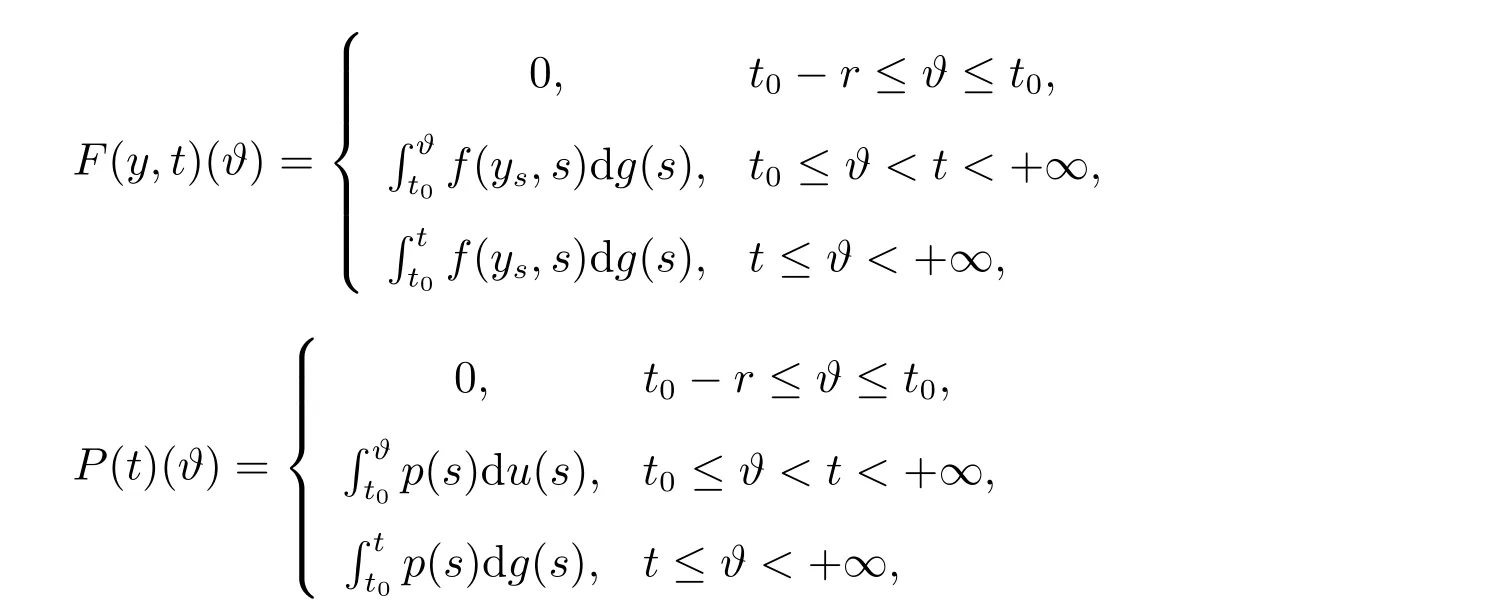
则有

且G∈F(Ω,h),其中G:Ω→G([t0−r,+∞),Rn).
引理6[7]设O⊂G([t0−r,+∞),Rn)是开集,且t∈[t0,+∞)时具有延拓性质,T={yt:y∈O,t∈[t0,+∞)},φ∈T,g,u:[t0,+∞)→R是不减函数,f:T×[t0,+∞)→Rn满足(H1)–(H3),且p:[t0,+∞)→Rn满足(H4),(H5),G:O×[t0,+∞)→G([t0−r,+∞),Rn)由(13)给定.
(i) 假设对于任意的y∈O,t∈[t0,+∞),如果y:[t0−r,+∞)→O是滞后型测度泛函微分方程
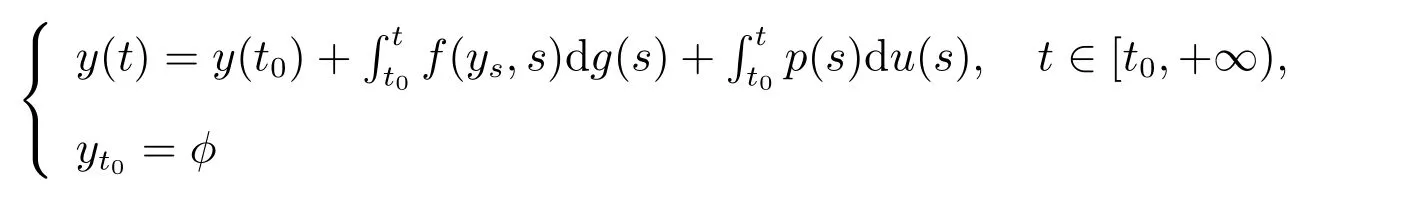
的解.
对任意的t∈[t0−r,+∞),有
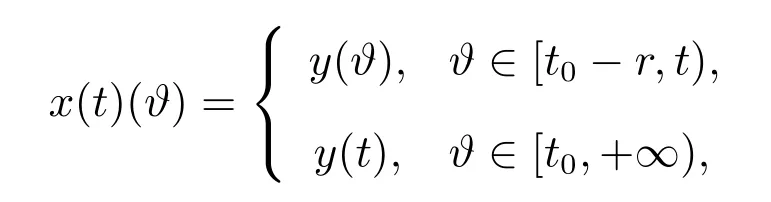
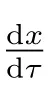
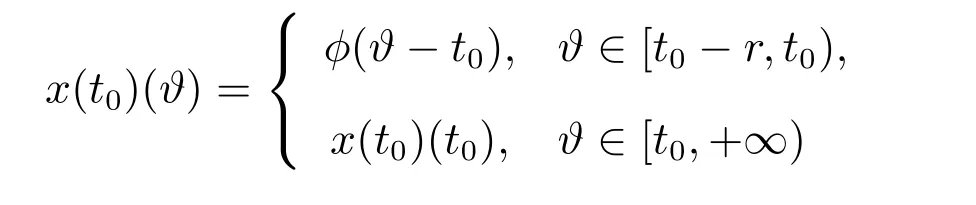
下的解,其中G由(13)式给定.
(ii) 相反地,G由(13)式给定,如果x:[t0,+∞)→O是广义常微分方程
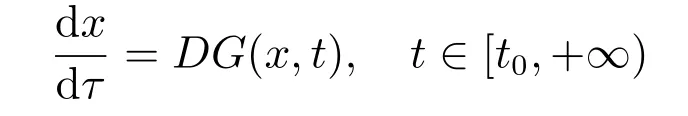
的解,且满足初值条件
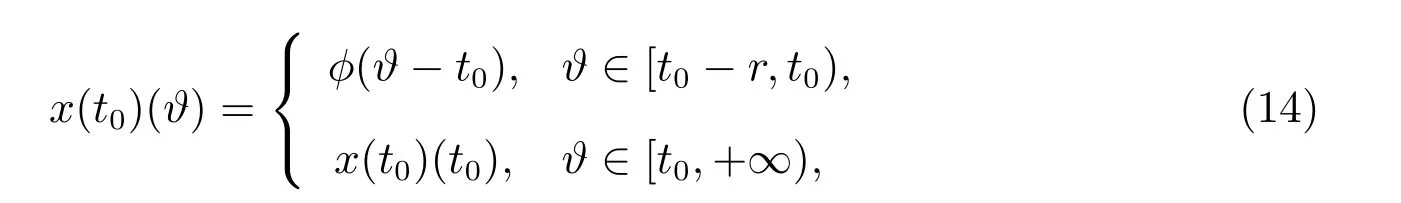
则函数y:[t0−r,+∞)→O是滞后型测度泛函微分方程
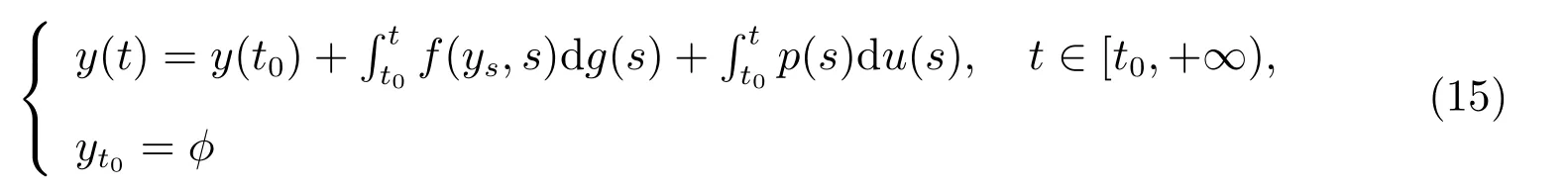
在初值条件
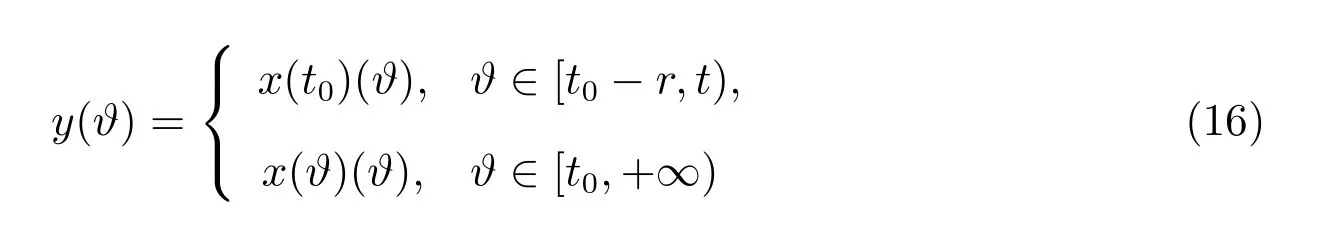
的解.
3 主要结果
本节,将讨论滞后型测度泛函微分方程(2)与受到扰动后的滞后型测度泛函微分方程(3)解对参数的连续依赖性.
定理1 设I⊂G([t0−r,+∞),Rn)是闭子集,O⊂I是开集,函数列Fk:O×[t0,∞)→Rn,对每一个k∈N0,(x,t)∈O×[t0,∞),Fk∈F(O×[t0,∞),h,ω),有
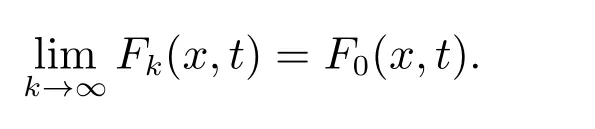
若存在一个序列函数xk:[t0,+∞)→O,k∈N0,t∈[t0,+∞),使
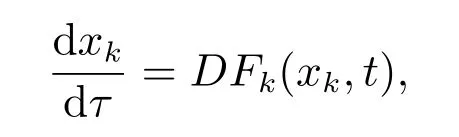
且对每个t∈[t0,+∞),有limk→∞xk(t)=x0(t),则有
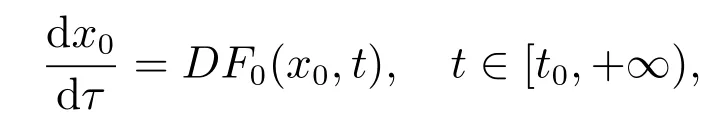
证明 由定义3知,对s1,s2∈[t0,+∞),k∈N0,有
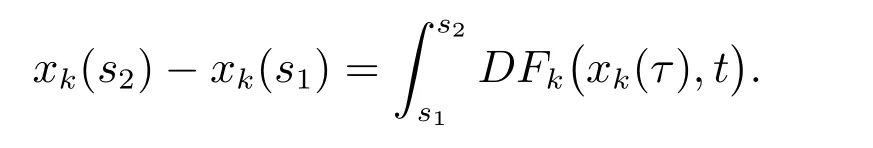
由引理2知
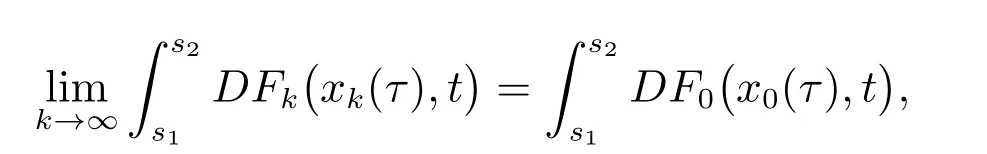
则Fk∈F(O×[t0,∞),h,ω),故对k∈N0[α,β]⊂[s1,s2],有
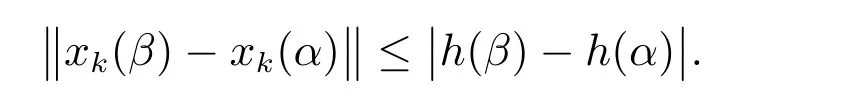
从而,当k→∞时,有
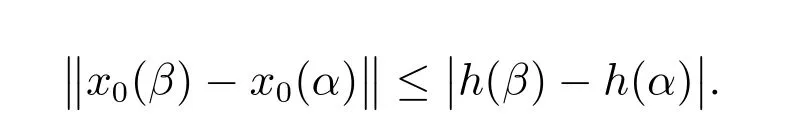
因h是正则的,故x0是正则的,即x0是有界变差的.又
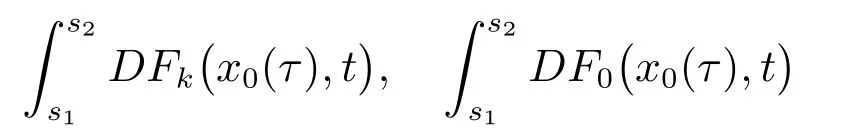
存在,则
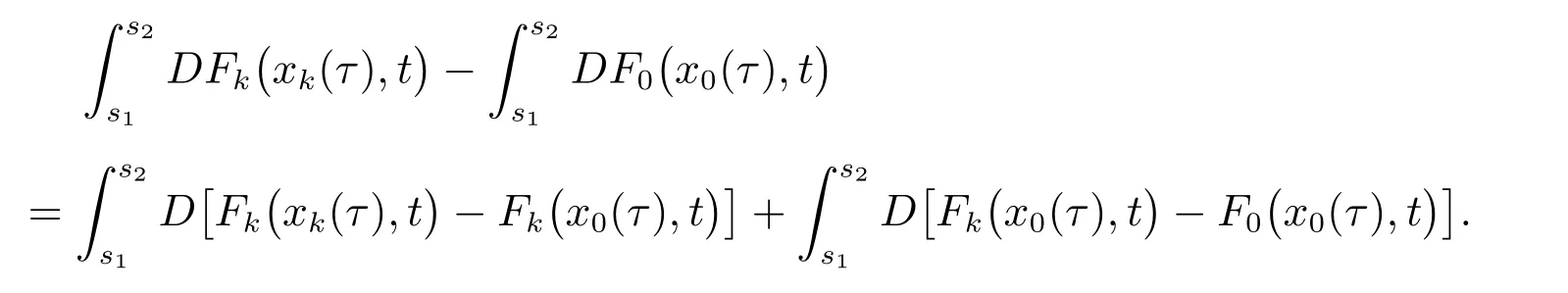
因为
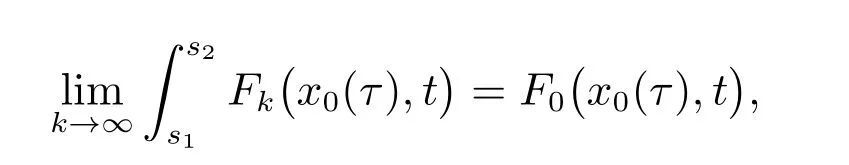
从而,上式第二个积分当k→∞时一致收敛于0.又
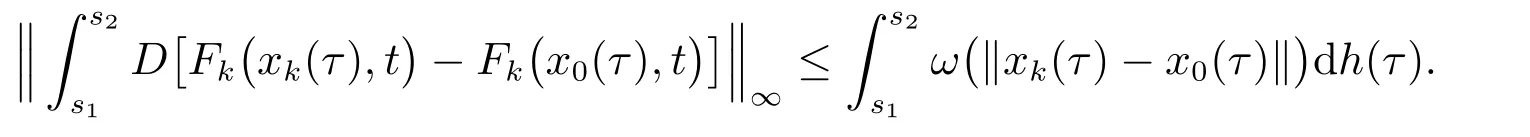
因为,对k∈N0,s1,s2∈[t0,+∞),有
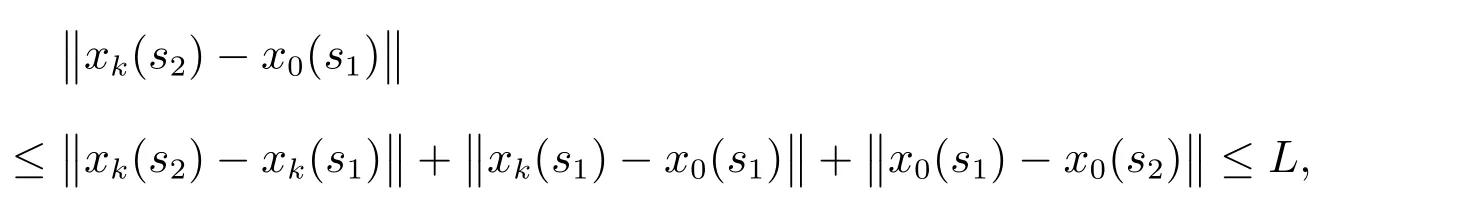
其中

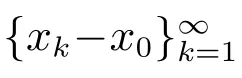
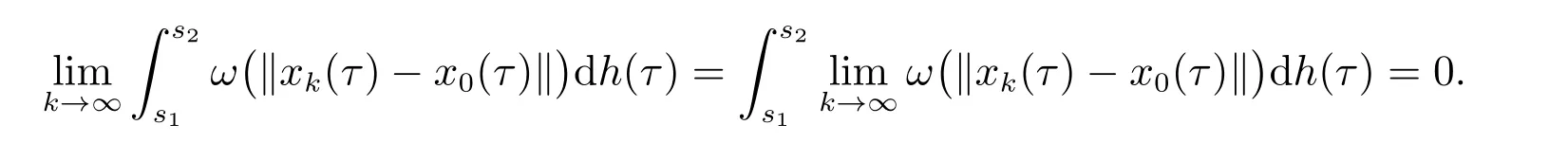
令
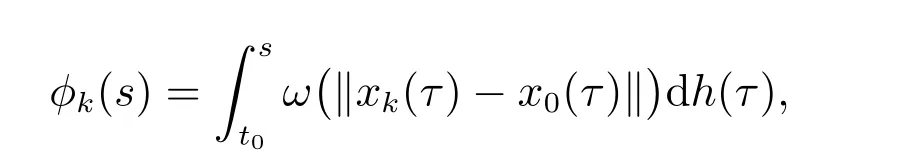
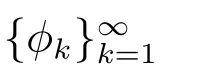
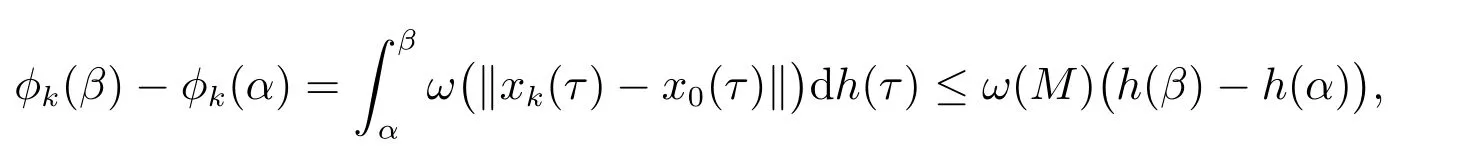
定理2 设I⊂G([t0−r,+∞),Rn)是闭子集,O⊂I是开集且具有延拓性质,T={yt:y∈O,t∈[t0,+∞)},g:[t0,+∞)→R是不减函数,ω:[0,+∞)→[0,+∞)是连续增加函数f:T×[t0,+∞)→Rn满足(H1)–(H3),F:O×[t0,+∞)→G([t0−r,+∞),Rn)由(9)给定,则F∈F(O×[t0,+∞),h,ω),其中h是不减的左连续函数,且
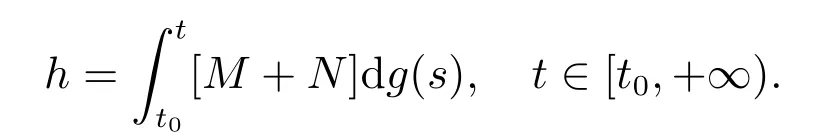
函数列fk:T×[t0,+∞)→Rn,k∈N0满足以下条件:
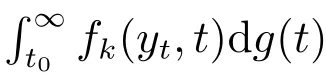
2) 对任意的y∈O,s1,s2∈[t0,+∞),存在一个常数M>0,使得
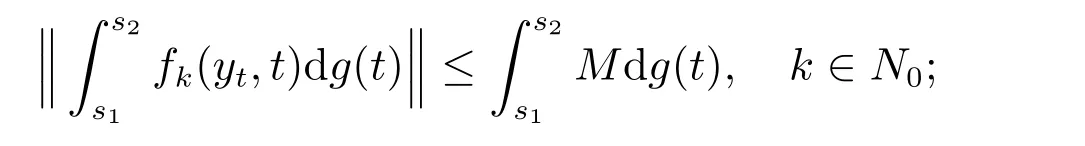
3) 对任意的y,z∈O,s1,s2∈[t0,+∞),存在一个常数N>0,且存在一个连续增加函数ω:[0,+∞)→[0,+∞),ω(0)=0,使得
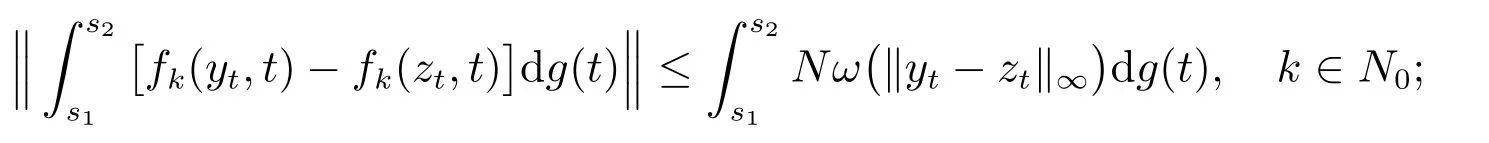
4) 对任意的y∈O,t∈[t0,+∞),有
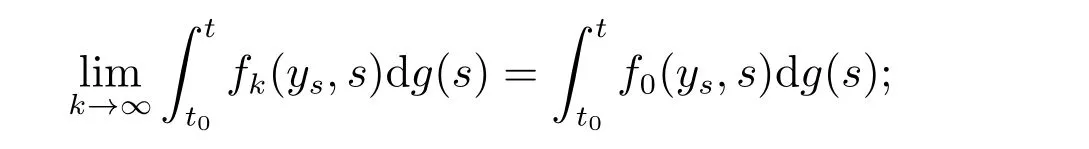
5) 对每个k∈N0,x∈O,t∈[t0,+∞),函数Fk:O×[t0,+∞)→G([t0−r,+∞),Rn),如下给定
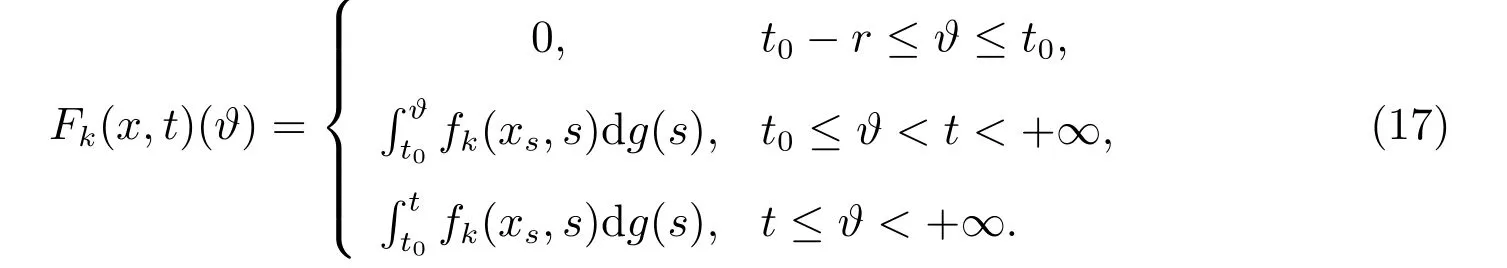
考虑到函数列φk∈T,k∈N0,使得在区间[−r,0]上有
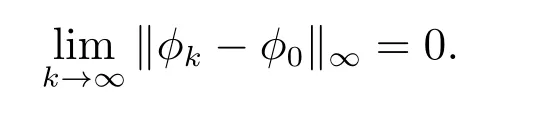
若存在一个k∈N0,函数列yk是Fk的解如下形式
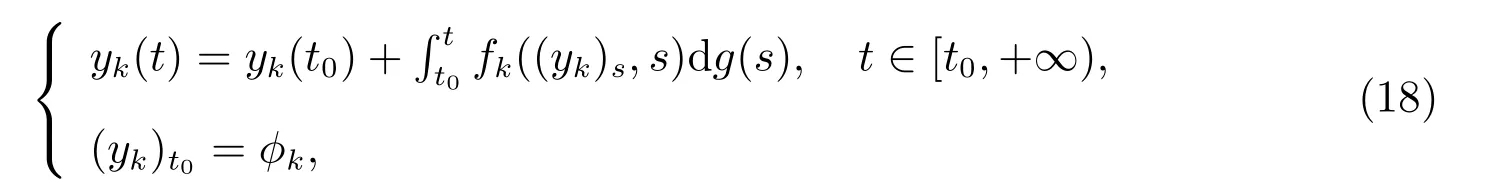
则存在一个函数y0∈O,使得在[t0,+∞)上有limk→∞‖yk−y0‖=0,则y0是F0的解如下形式
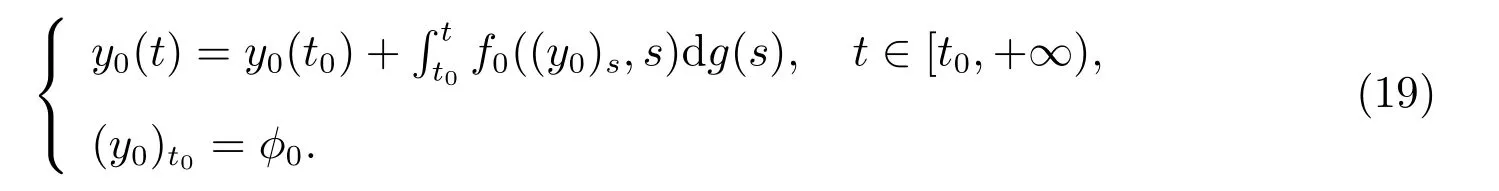
证明 由条件(H1)可知,定义的F积分存在,对任意的y∈O,t0≤s1 因此,对任意的y∈O,t0≤s1 由定义4及(H3)条件,如果y,z∈O,t0≤s1 由定理1知对每个x∈O,t∈[t0,+∞),有limk→∞Fk(x,t)=F0(x,t),通过奥斯古德定理[6],对每个x∈O,t∈[t0,+∞),有limk→∞Fk(x,t+)=F0(x,t+),而且因为I是闭子集即有F0(x,t)∈I.由前面证明可知,对每个k∈N0,Fk∈F(O×[t0,+∞),h,ω),其中h是不减的左连续函数,且对 又因为limk→∞Fk(x,t)=F0(x,t),则有F0∈F(O×[t0,+∞),h,ω),对k∈N0,t∈[t0,+∞),令 由xk的定义,对于t∈[t0,+∞),有limk→∞xk(t)=x0(t),根据定理1,x0是 的解,故而确保y0满足 因此,我们通过运用广义常微分方程与滞后型测度泛函微分方程的等价关系,得到了方程(2)的解对参数的连续依赖性定理. 定理3 设I⊂G([t0−r,+∞),Rn)是闭子集,O⊂I是开集,函数列Gk:O×[t0,∞)→Rn,对每一个k∈N0,(x,t)∈O×[t0,∞),Gk∈F(O×[t0,∞),h,ω),有limk→∞Gk(x,t)=G0(x,t).若存在一个序列函数xk:[t0,+∞)→O,k∈N0,t∈[t0,+∞),使 且对每个t∈[t0,+∞),有limk→∞xk(t)=x0(t),则有 证明 由文献[7]知对s1,s2∈[t0,+∞),k∈N0,有 显然由定理1知 则Fk∈F(O×[t0,∞),h,ω),故对k∈N0,[α,β]⊂[s1,s2],有 从而,当k→∞时,有 因h,h2正则的,故x0正则的,即x0是有界变差的.又 存在,则 因为 从而上式第二个积分当k→∞时,一致收敛于0.又 因为对k∈N0,s1,s2∈[t0,+∞),有 其中 且 由于h2是不减函数,则h2是有界变差的,故是正则的,则对k∈N0,t∈[t0,+∞),Pk∈G([t0−r,+∞),Rn),有limk→∞‖Pk(t)−P0(t)‖∞=0,因此,对s∈[t0,+∞),k∈N,令 定理4 设I⊂G([t0−r,+∞),Rn)是闭子集,O⊂I是开集,g,u:[t0,+∞)→R是不减函数,T={yt:y∈O,t∈[t0,+∞)},f:T×[t0,+∞)→Rn满足(H1)–(H3),P:[t0,+∞)→Rn满足(H4)和(H5),G:O×[t0,+∞)→G([t0−r,+∞),Rn)由(13)给定,则有G∈F(O×[t0,+∞),h,ω),其中h=h1+h2是不减的左连续函数,且 证明 由条件(H1)可知,定义的F积分存在,对任意的y∈O,t0≤s1 由条件(H4)可知,定义的P积分存在,故对任意的y∈O,t0≤s1 因此,由定理2知对任意y∈O,且t0≤s1 且有 同理,由定理2知,如果y,z∈O,t0≤s1 故对任意的y∈O,且t0≤s1 由定义4及(H3)条件知,如果y,z∈O,t0≤s1 定理5 设I⊂G([t0−r,+∞),Rn)是闭子集,O⊂I是开集且具有延拓性质,T={yt:y∈O,t∈[t0,+∞)},g,u:[t0,+∞)→R是不减的函数,函数列fk:T×[t0,+∞)→Rn,pk:[t0,+∞)→Rn,k∈N0满足以下条件: 2) 对任意的y,z∈O,s1,s2∈[t0,+∞),存在一个常数N>0且存在一个连续增加函数ω:[0,+∞)→[0,+∞),ω(0)=0,使得 3) 对任意的y∈O,t∈[t0,+∞),有 5) 对每个k∈N0,s1,s2∈[t0,+∞),存在一个常数K>0,使得 6) 对任意的y∈O,t∈[t0,+∞),有 7) 对每个k∈N0,x∈O,t∈[t0,+∞),函数Gk:O×[t0,+∞)→G([t0−r,+∞),Rn),如下给定 函数Pk∈G([t0−r,+∞),Rn),k∈N0如下给定 则有 考虑到k∈N0,t∈[t0,+∞),Pk∈G([t0−r,+∞),Rn),有 且存在函数列φk∈T,k∈N0,使得在区间[−r,0]上有limk→∞‖φk−φ0‖∞=0. 若存在一个k∈N0,函数列yk是Gk的解如下形式 则存在一个函数y0∈O,使得在[t0,+∞)上有limk→∞‖yk−y0‖=0,则y0是G0的解如下形式 证明 由定理1可知,对每个x∈O,t∈[t0,+∞),有limk→∞Fk(x,t)=F0(x,t),且F0∈F(O×[t0,+∞),h,ω),又有k∈N0,t∈[t0,+∞),Pk∈G([t0−r,+∞),Rn),则有 从而P0∈G([t0−r,+∞),Rn),故对每个x∈O,t∈[t0,+∞),有limk→∞Gk(x,t)=G0(x,t),根据奥斯古德定理对每个x∈O,t∈[t0,+∞),有limk→∞Gk(x,t+)=G0(x,t+),而且因为I是闭子集即有G0(x,t)∈I.由定理3和定理4知,对每个k∈N0,Gk∈F(O×[t0,+∞),h,ω),其中h=h1+h2是不减的左连续函数,且 由limk→∞Gk(x,t)=G0(x,t),则有G0∈F(O×[t0,+∞),h,ω),对k∈N0,t∈[t0,+∞),令 由xk的定义,对于t∈[t0,+∞)有limk→∞xk(t)=x0(t),根据定理3和定理4,对任意的t∈[t0,+∞),有 是广义常微分方程 的解,故而确保y0满足