水土保持多尺度因子探析

王淑芹

(朝阳市喀左县水利局，辽宁 朝阳 122300)

0 引 言

一般地，在复杂浅层地下水发育区域、三角洲或冲击平原等复杂地表径流区域和第四系发育的山地丘陵坡地等均会有水土流失的发生[1]。因此，地表径流的水土冲刷作用及浅层地下水的流体动力过程在很大程度上决定了水土流失的影响因子。然而，第四系的表层稳定性主要取决于浅层地下水径流量、地表径流量、地表坡度和第四系发育程度等因子，水土流失过程也会受到抑制土壤侵蚀的人工构筑物规模及地表植被因子的影响[2-4]。对此，为构建Arc GIS模型可以引入加权累加法，通过加权能够提供水土保持的因子反映可能引起水土流失的动力过程，即以加权的Arc GIS模型数据衡量区域水土保持能力。

1 水土保持多尺度因子

1.1 多尺度因子的构建

1.1.1 地表坡度与第四系厚度

借鉴相关地质资料，在厚度较小的情况下第四系发育极不稳定，在存在一定坡度且厚度较大的条件下地质滑坡概率增大，并随之增加水土保持的难度，因此要联合分析地表坡度与第四系厚度[5]。水土保持难度与地表坡度、第四系厚度存在逆幂函数及二次函数的关系，故两者相乘可确定综合表达式如下：

(1)

式中：e为自然常数；M、N为X和Y象限的位移值；α为第四系厚度系数；B、β为坡度系数的修正量与地表坡度系数。通过约定规律常数表以更好的确定α、β值，如表1。

表1 第四系厚度和地面坡度因子赋值表

从表1可看出，由于式(1)已按照抛物线与逆幂率规律对相应的α、β值分布规律进行了数学表达，因此在表1中的α、β赋值符合线性规律，无需开展非线性赋值的数学关系分析。对两组因子线性赋值的主要目的就是更加简化B、M、N等待回归因子的数学意义，进一步提高函数设计过程中的自由度。

1.1.2 构筑物与地表植被

可以近似的用线性关系反映水土保持构筑物和地表植被促进水土保持能力的作用，其中对水土保持具有较强支持度的有灌木和乔木覆盖率，而支持度较弱的有草本覆盖率。挡土墙、引水渠、拦水沟等均可作为地表水土保持构筑物，其完善程度与水土保持能力存在线性关系，可利用加权累加法控制多种影响因素的数据，具体如下：

N2=0.60(0.15λL+0.35λM+0.50λM)+0.40γ

(2)

式中：γ为地表构筑物的传导因子；λL、λM、λH依次代表草本植物、灌木和乔木的覆盖率传导因子。通过约定规律常数表以更好的确定λL、λM、λH、γ值，如表2。

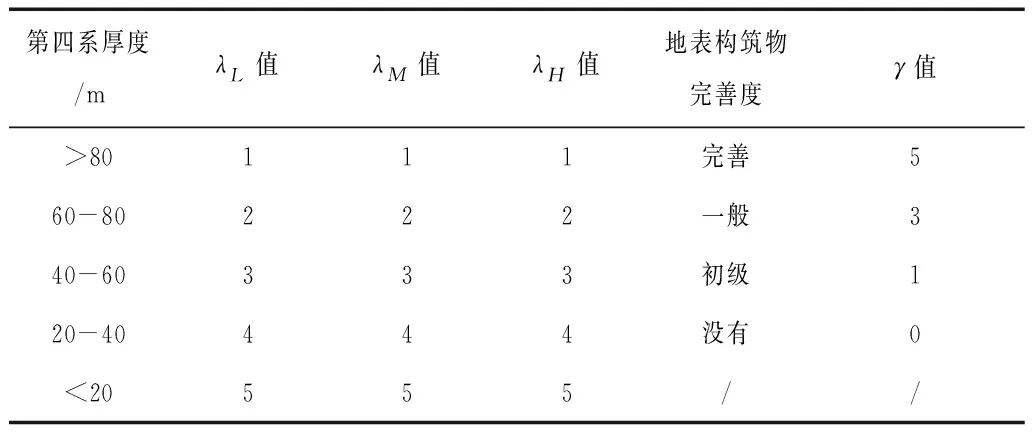
表2 地面植被和构筑物因子赋值表

通过分析可知，公式(2)已经给出表2中需要传导的数据加权参数，因此可按照表2中的线性关系对λL、λM、λH3个因子赋值，无需开展最终因子与3个因子之间的实际加权特征，由此可以实现更高自由度的实际加权因子管理控制[6]。

同理，可利用线性关系对表2中的γ赋值。其中，“完善”代表区域内存在水土保持合理维护且功能健全的地表构筑物系统；“一般”代表区域内已实施功能无法有效或者全部发挥的辅助措施，水土保持地表构筑物体系相对完善；“初级”代表区域内已存在初步控制水土流失的设施，如人造水渠等构筑物；“没有”代表在分析区域外扩100范围内及分析区域内没有任何能够辅助控制水土保持的地表构筑物。

1.1.3 地下渗流与地表径流

区域内地表径流量来源于便携式或者移动式水文站监测数据，结合现有研究资料，水土保持难度随地表径流量的增大而增加[7-8]。以钻孔抽水数据为基础合理确定地下径流量，可利用以下表达式作为其控制函数，即：

(3)

式中：ξU、ξD为区域内地表与地下径流数据。考虑到ξU与ξD之间存在逆函数关系，故函数分布特征分析时应取倒数，近数轴0点的数据关系使用对数函数进行放大处理[9]。通过约定规律常数表来更好的确定实际传导因子值，如表3。

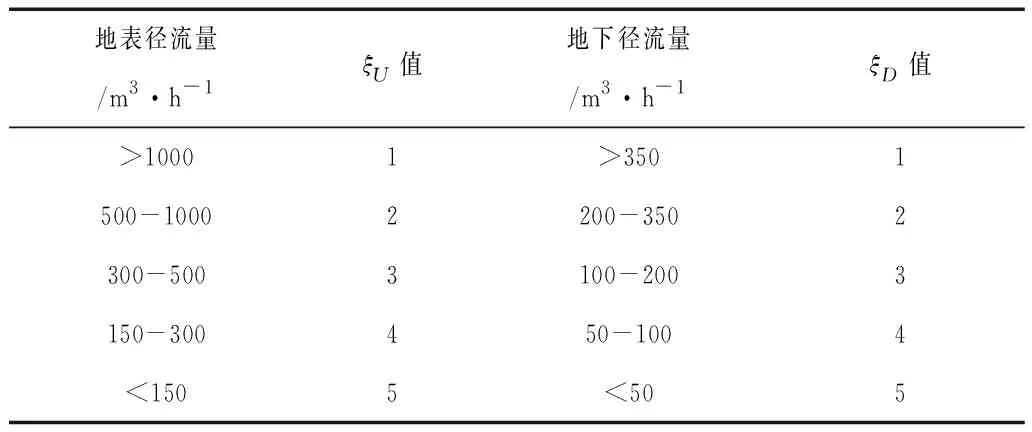
表3 地表与地下径流因子赋值表

从表3可看出，在较小径流量条件下ξU、ξD的赋值较小，在较大径流量条件下ξU、ξD的赋值较大，其统计学本质并非描述的水土保持数据，而是描述的水土流失数据。因此，为增加加权因子的统计学意义可以利用倒数函数对式(3)进行调用。

1.2 整体水土保持措施因子

综上分析，N1、N2、N3依次代表地质地层、地表附着物与地表植被、水体环境对水土保持能力的影响。采用加权累加法对这3个因子进行处理，以构建整体因子表达式如下：

N=0.55N1+0.20N2+0.25N3

(4)

通过预估N1、N2、N3因子的作用机制确定其加权因子值为0.55、0.20、0.25，并且后续仿真数据分析表明以上加权因子能够符合实际研究需求。

2 实例仿真分析

2.1个案特征

以辽西低山丘陵区为例，选择典型地块面积20km×20km为研究对象。区域内60%以上为坡度5°-12°的山体，其最大坡度为18°，境内分布有2条大凌河支流，径流量为110-320m3/s和160-380m3/s。研究区山区、坡积平原区和淤积平原区第四系厚度0-2.6m、1-12m、5-35m，平均值为0.62±0.15m、5.78±0.55m、12.65±3.12m。河流最大水深1.5m，底部为厚度1.2-18.0m的第四系，现状较发育。

将研究区利用Arc GIS软件划分成25m×25m的基本单元，从而形成800×800共64万个方格。然后按照前文所述方法对每个方格的N1、N2、N3因子赋予相应的数值，以检测的水土流失情况与河流载沙量之间的关系，评判以上模型的水土保持能力及其抑制土壤侵蚀的程度。

2.2 实证分析

采用加权法对N1、N2、N3值进行加权计算，即通过对所有单元N1、N2、N3各项均值的计算确定最终的N值。每月采集1次计算河流载沙量，结合区域内的地质条件，在采集过程中重新计算或补充调查N1、N2、N3、N值，结果如表4。

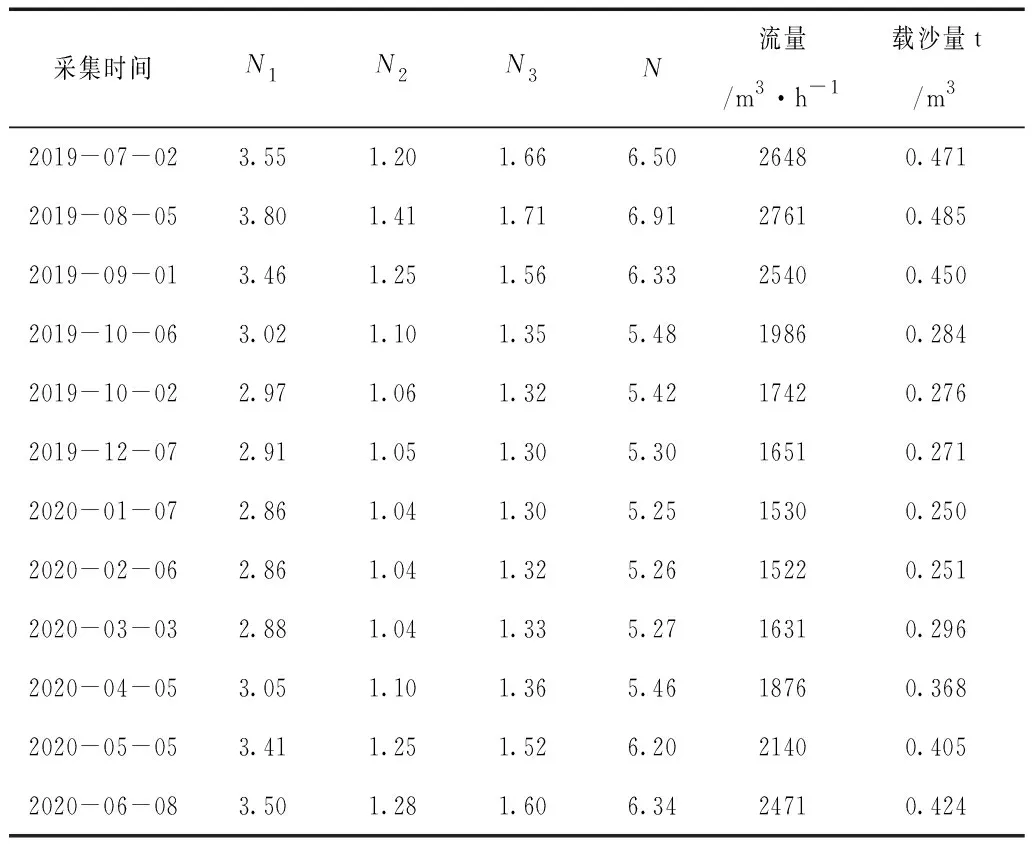
表4 实证分析数据表

从表4可知，该河流的载沙量与河道流量均存在较大的波动，但变化幅度相对较小的为N值的32.4%，其最小和最大值为5.25、6.91；载沙量最低与最高值分别出现在2月、8月，其值为0.251t/m3和0.485t/m3，变化幅度达到93.3%；总体上，载沙量变化趋势与N值基本统一，数据变化可近似符合线性特征。因此，可进一步可视化处理表4中的数据，如图1。

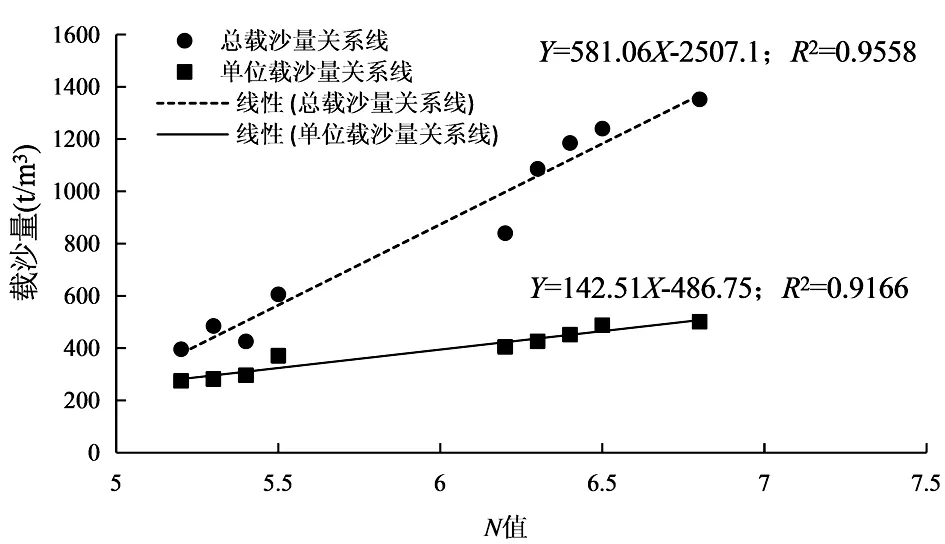
图1 线性拟合关系图

可见，N值与总载沙量、单位载沙量数据符合Y=581.06X-2507.1(R2=0.9558)、Y=142.51X-486.75(R2=0.9166)回归公式，两者的值均满足>0.9的检验要求。此外，拟合分析也验证了水土保持实际测量值与文中设置的多尺度因子具有较高的吻合度，该加权模式对优化水土保持措施布局具有重要意义[10]。

3 结 论

从环境学与地质学的角度，探究了地下和地表径流、地表构筑物和地表植被、第四系发育情况和地貌形态等因子与区域水土保持能力之间的关系，在此基础上利用加权累加法构建了水土保持因子体系。实证分析时，通过限定水土流失与河流总载沙量数据、单位载沙量数据，以统计学分析了实际测量数据与设定因子之间的相关性，结果显示水土保持实际测量值与文中设置的多尺度因子具有较高的吻合度，该加权模式对优化水土保持措施布局具有重要意义。