考虑多层软土地基固结的路堤整体稳定性分析方法

张瑜 肖世国

1.西南交通大学地质工程系，成都610031；2.西南交通大学高速铁路线路工程教育部重点实验室，成都610031

实际路基工程中常涉及软土地基［1-2］，软土地基上路堤稳定性是工程实践中关注的一类重要问题。然而，由于软土地基的排水固结过程较长，在路堤填筑完成后地基土的强度往往并没有充分发挥［3］。因此，地基土的固结度是路堤-地基整体稳定性分析中的关键因素，应充分考虑。

关于单一软土地基固结问题，Terzaghi提出了著名的饱和土体一维固结理论［3］，Biot［4］进一步建立了三维固结理论。在此基础上，文献［5-11］研究了双层地基的一维固结问题，给出了荷载随时间任意变化及起始孔压沿深度任意分布情况下双层地基一维固结解答，讨论了双层地基一维固结特征，并计算分析了实际工程中的地基沉降。但相关方法尚未用于路堤-地基整体稳定性分析中。对于考虑固结度的地基稳定性分析的方法主要为有效应力法和有效固结压力法。有效应力法可得出土体抗剪强度与有效应力增量之间的关系表达式，但在工程中很难估算出孔隙水压力准确值，因此限制了该法的实际应用。有效固结压力法考虑土体压缩而忽略剪缩效应引起的强度增长，在抗剪强度表达式中体现了土体抗剪强度增量与主应力增量及点固结度之间的关系。

实际上，除了单层和双层地基外，多层地基在工程实践中更为常见。因此，本文基于以往的双层地基一维固结计算方法，以三层为例进一步拓展分析多层地基的竖向固结问题，推导任意时刻地基不同点处抗剪强度与该点固结度的函数关系式。在此基础上，采用三种经典的极限平衡条分法（Fellenius法［12］、简化Bishop法［13］、Morgenstern-Price法［14］），给出考虑地基固结度的多层软土地基上路堤整体稳定性分析方法，进而确定多层软土地基固结度对路堤-地基整体稳定性的影响特征，并讨论现行铁路规范中相关计算方法所存在的问题。

1 路堤下多层软土地基一维固结分析

1.1 基本假定与路堤荷载

为便于简化分析问题，采用如下基本假定［5］：①地基中土体均质且完全饱和；②土粒和孔隙水不可压缩；③地基土中只发生竖向渗流，水在地基土中渗流符合Darcy定律；④在渗透固结过程中，土的渗透系数和压缩系数均为常数。

考虑实际路堤的分段填筑施工过程，作用于地基上的路堤荷载视为随时间t分段变化的函数q（t）。

1.2 路堤荷载下地基竖向附加应力

实际的路堤填筑体在横断面上呈梯形，因此，路堤荷载可视为中间均布条形荷载与两侧三角形分布条形荷载的组合，如图1所示。

地基表面在均布条形荷载p作用下，基于Boussinesq理论可得地基中任一点的竖向应力σˉz1、水平应力σˉx1和剪应力τˉxz1，其表达式分别为

式中：a为中间均布条形荷载分布长度的一半；x、z分别为地基中一点M的横、纵坐标。

单侧三角形条形荷载分布长度为L，地基表面在左、右两侧三角形分布条形荷载p1(x)=ξp∕L(0＜ξ＜L)与p2(x)=(L-ξ)p∕L(0＜ξ＜L)作 用 下，基 于Boussinesq理论［16］也可得地基中任一点的竖向应力σˉz2（下标2表示左侧荷载，余同）与σˉz3（下标3表示右侧荷载，余同）、水平应力σˉx2与σˉx3以及剪应力τˉxz2与τˉxz3，其表达式分别为

根据叠加原理，将式（1）—式（3）相应叠加，可得路堤荷载产生的地基中任一点的竖向附加应力水平应力和剪应力分别为

地基中任一点处的总竖向压应力σjz、总水平应力σix、总剪应力τjxz分别为相应的自重应力σjz0、σjx0、τjxz0与式（4）所确定的附加应力之和，即

1.3 三层地基竖向固结度

三层地基一维固结模型如图2所示，图中hi为第i土层厚度，H为渗透地层总厚度，cvi为第i土层的竖向固结系数，Esi为第i土层的压缩模量。

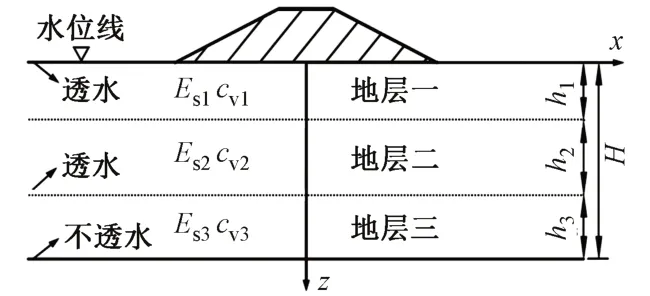
图2 三层地基一维固结模型

可通过满足三层地基固结的边界与连续性条件及初始条件来求解一维固结微分方程，即

式中：ui为第i土层任意点的超静孔隙水压力。

式（6）满足：①边界条件z=0时，u1=0；z=H时，②连续性条形z=hi（i=1，2）时，ui=ui+1；其中，kvi为第i土层的竖向渗透系数。③初始条件t=0时，ui=0（i=1，2，3）。

于是，地层一、地层二、地层三的固结度及超静孔隙水压力的解为

式 中：Cmi为 无 量 纲 系数，Cmi=2∕{λm[1+为 特 征 方 程sin（μ2λm）cos（μ3λm）=0的正根，μ2、μ3分别为第2、第3层地层竖向固结系数比的平方根，Ami为无量纲系数；gmi和βmi为计算系数为第i层地层竖向固结系数比的平方根为无量纲系数为第i土层任意点的点固结度。

当i=1时，Am1=1，Bm1=0；当i＞1时，Ami、Bmi计算式为

2 关联固结度的路堤-地基整体稳定性分析

根据点固结度概念、Mohr-Coulomb强度准则及有效应力原理，可得地基中一点处沿某一方向（与水平向夹角为α）抗剪强度τfi与固结度Ui之间的关系表达式为

基于式（11）确定抗剪强度，针对路堤-地基体系，可采用经典的极限平衡法（Fellenius法、简化Bishop法和Morgenstern-Price法）分析其整体稳定性。

3 实例分析与讨论

3.1 实例分析

中铁二院工程集团有限责任公司承担设计的孟加拉帕德玛大桥铁路连接线工程中某工点路堤横断面如图3所示，地表以下为三层软黏土地基，其下部为工程性质良好的硬塑黏土层（可视为不透水土层）。现场试验所得填土及地基土主要物理力学参数见表1，路堤填高7 m，填方坡率为1∶2。常水位线位于地表处。路堤整体用180 d填筑完成，分为三阶段填筑（图4），每一阶段填筑与静置时间均为30 d。

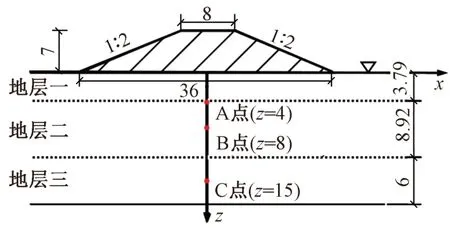
图3 实例铁路路基横断面示意

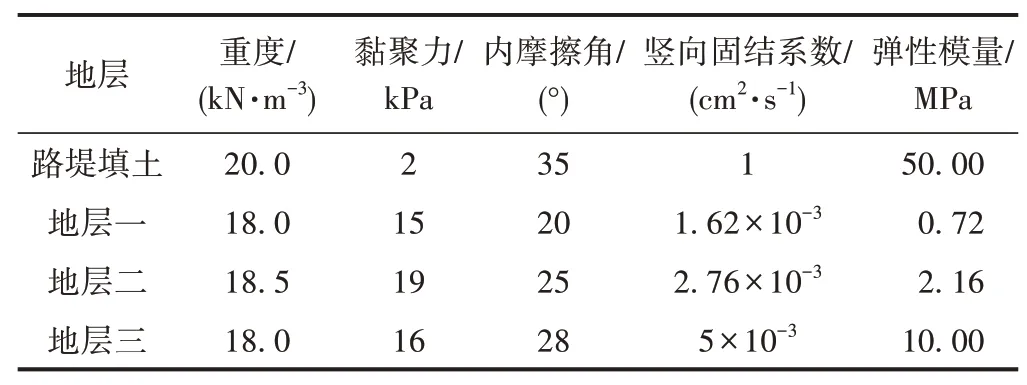
表1 土体主要物理力学参数

图4 路堤填筑荷载随时间变化曲线

根据前述分析方法，可计算得到在路基中心线（x=0处）不同深度下超静孔隙水压力与固结度随时间的变化曲线，见图5。可知：随着时间增加，超静孔隙水压力呈现出先阶梯式增大后变小的趋势。在路堤填筑期，超静孔隙水压力随荷载增大而增大；在填筑暂停期，超静孔隙水压力减小；在路堤整体填筑完成后，地基不同深度处超静孔隙水压力随时间近似呈线性消散，点固结度近似呈线性增大。此外，随深度增加，相同时刻的点固结度非线性增大。

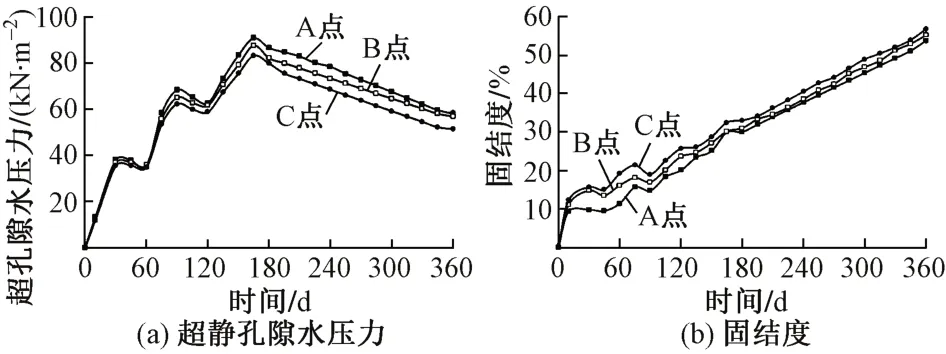
图5 不同深度处超静孔隙水压力与固结度随时间的变化曲线

路堤-地基整体稳定系数随计算参考点（可任取，为便于表述，这里取x=0、z=1 m处）的固结度变化曲线见图6。可知：随着固结度的增大，稳定系数总体呈非线性增大。在相同固结度下，Fellenius法计算的稳定系数最小，Morgenstern-Price法最大，简化Bishop法与Morgenstern-Price法结果相近。在固结度为30%和90%的情况下，简化Bishop法计算所得的稳定系数分别为1.19、1.37，即该点固结度由30%升至90%时，路堤-地基整体稳定系数提高15%。

图6 整体稳定系数随固结度（x=0、z=1 m）变化曲线

固结度为50%、80%条件下最危险滑面（简化Bishop法）及滑面上不同点处（x=0、z=1 m，滑面上等距选择5个监测点）的固结度见图7。可知：随着该点固结度的增大，最危险滑面穿过地基土的长度逐渐减小。这是由于地基软黏土强度远低于路堤填土强度，地基土固结度越小，其强度越低，最危险滑面就越深，整体稳定性越差。

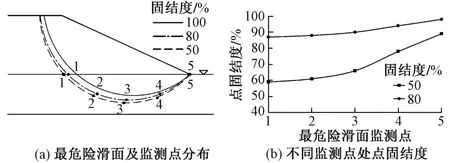
图7 不同固结度时最危险滑面（简化Bishop法）及不同监测点处固结度

3.2 数值模拟分析

为进一步检验前述理论计算方法的合理性，采用FLAC 3D数值模拟方法对实例进行分析，数值模型如图8所示。模型用六面体单元划分网格，共有36 232个实体单元和40 995个节点。同时为消除边界效应影响，基于实际工程条件，自路堤坡脚处向左右两边各取5倍路堤填高（35 m）、深度与宽度（平面外）分别取18.71 m和1倍路堤填高（7 m）作为数值模型几何边界。模型底面采取固定约束，模型四周采取水平位移约束；地基顶面为透水边界、底面为不透水边界。土体采用理想弹塑性本构模型、摩尔库仑强度准则和非关联流动法则。数值模拟中采用强度折减法计算路堤-地基整体稳定系数。

图8 实例FLAC 3D分析模型

路堤荷载下地基竖向应力分布及路堤底面以下深度0.1 m处（即x=-18～18 m、z=0.1 m）的竖向应力分布见图9。可知：在路堤荷载作用下地基中竖向应力呈中间大两边小的梯形分布，数值模拟结果与竖向应力的经典理论计算值在大小及分布特征方面均吻合良好，说明了数值模型的合理性。

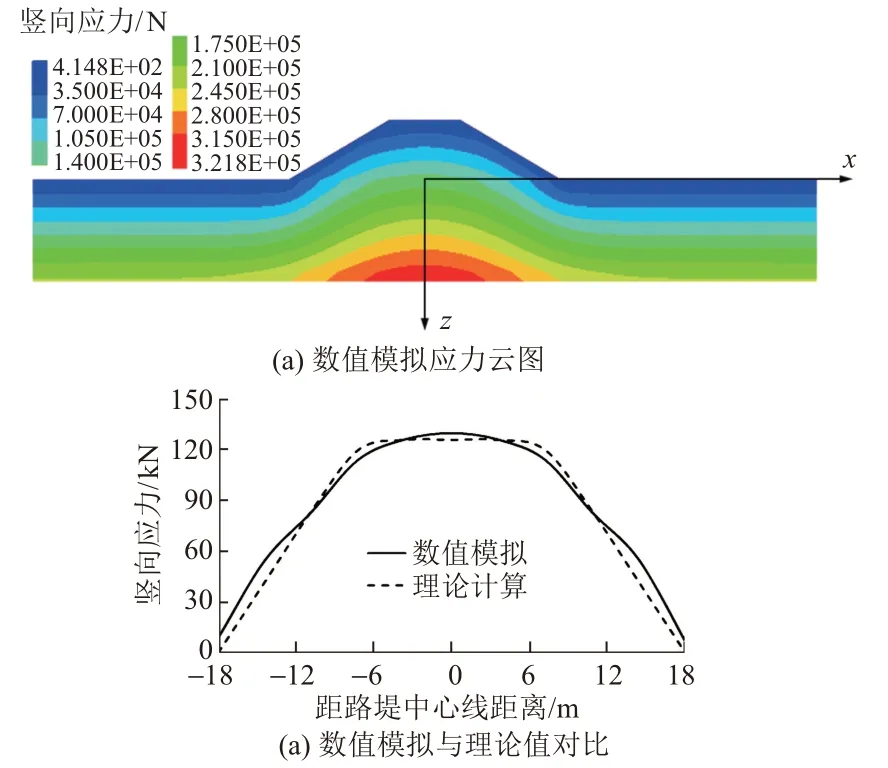
图9 地基中的竖向应力

由稳定系数计算结果（参见图6）可见，FLAC 3D所得稳定系数随计算参考点的固结度增大而增大，计算值均大于三种极限平衡条分法结果。在该点固结度为50%、80%时，FLAC 3D所得稳定系数分别为1.36、1.44，与简化Bishop法结果的相对误差分别为5.9%、6.7%。两种固结度时极限状态下模型的竖向应力见图10。可知，最危险滑面均经路堤填土和地基土层一，从路堤坡脚外穿出。基于简化Bishop法得到的滑面位置与数值模拟结果较为接近，本文方法所得的滑面位置略深（向下），即本文方法略偏保守。

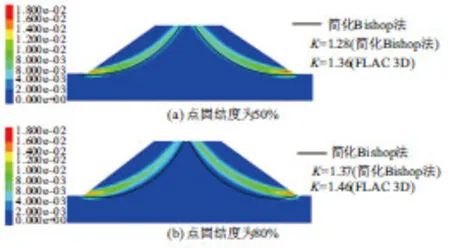
图10 FLAC 3D得到的最大剪应变增量云图

3.3 与规范法对比分析

由于路堤填土施工过程较长（本例为180 d），因此，地基土的抗剪强度指标可采用固结快剪值。基于Fellenius法的本文方法（采用固结快剪指标）与TB 10106—2010《铁路工程地基处理技术规程》中计算方法（采用快剪指标）得到的路堤-地基整体稳定系数随计算参考点（x=0，z=1 m）的固结度变化曲线见图11。

图11 地基-路基整体稳定系数与固结度（x=0、z=1 m）关系

由图11可知，仅当该点固结度达到90%及以上时，两种方法计算结果才趋于一致；而随着固结度的减小，本文方法的稳定系数显著大于规范法结果。为了说明其差异原因，将本文与规范的稳定系数求解式相减，即得稳定系数差ΔK（本文-规范）为

式中：Wdi为第i土条中地基土自重；cgi、ϕgi分别为地基土固结快剪黏聚力及内摩擦角；cqi、ϕqi分别为地基土快剪黏聚力及内摩擦角。

图12 本文与规范法结果差异分析图示

4 结论

1）针对路堤填土的梯形荷载作用模式，基于Boussinesq理论求解地基中附加应力，并结合三层地基的边界条件、连续性条件及初始条件，通过求解一维固结微分方程，得到在梯形路基荷载作用下三层软土地基中超静孔隙水压力与固结度表达式，确定其随时间及空间的非线性变化特征。

2）基于有效应力原理得到地基中不同点处抗剪强度与点固结度的函数关系，将其引入边坡稳定性的极限平衡分析法中，给出了基于Fellenius法、简化Bishop法、Morgenstern-Price法的路堤-地基整体稳定系数及最危险滑面的求解方法，确定路堤-地基整体稳定性与地基土固结度的关系。

3）与TB 10106—2010《铁路工程地基处理技术规程》所规定的路堤-地基整体稳定性分析方法相比，本文方法计算结果在较低的地基固结度情况下大于规范方法，而当地基固结度较高时（达到90%），二者计算结果较为接近。规范法计算结果偏保守的主要原因在于其计算地基固结致滑面强度增长时，只考虑了滑面穿过地基段相应的路堤填土重力，却忽略了地基土自重。