级间导叶数对水轮机模式液力透平性能的影响

李延频，蒋雨煊，张自超，陈金保，陈德新

（1.华北水利水电大学电力学院，郑州450000；2.武汉大学动力与机械学院，武汉430072）

0 引 言

液力透平作为一种能量回收装置，广泛用于工业、电力、农业等领域，通过将来流的动能转化成机械能，从而实现对液体能量的回收。现阶段，液力透平的结构形式主要包水轮机模式，反转泵模式和专用液力透平。针对不同能量等级的回收，液力透平又有单级和多级液力透平之分，提高液力透平性能对提高能源利用率有现实意义［1］。

对于液力透平，导叶是关键的过流部件，关于导叶的研究，杨军虎［5］采用CFD 软件对首级导叶数为7，9，11 的3 种液力透平进行数值模拟，发现效率随导叶片数增多而提高，且较无导叶时透平最高效率点的流量增加、压头降低，导叶数为11 时其变化幅度值最小。YABIN T［6］从理论上分析了影响多级能量回收水轮机性能的主要因素，发现转轮导叶出口段边缘圆弧半径是影响水轮机水力效率的决定性因素。纪运广［7］在液力透平转轮进口处添加导叶减少了水力损失从而使得效率得到提高，同时基于CFD 软件对不同导叶开度下的液力透平内部流场进行了分析。史广泰［8］研究了首级导叶数对液力透平机组工作稳定性的影响，发现首级导叶数增加，叶轮内部的最大脉动幅值减小，对尾水管的脉动幅值影响较小。Timoshevskiy M［9］对高压水轮机导叶缩尺模型的二维水翼绕流紊流结构的试验研究结果进行了分析研究。通过上述研究可以发现，导叶对透平的性能影响显著，但这些研究都仅针对于单级液力透平，而对于多级液力透平而言，级间导叶的损失也占很大一部分［10］。王亚猛［11］对多级水轮机模式液力透平同径正反导叶进行研究，发现优化级间导叶后对整个液力透平水力效率得到了提高。

现阶段，大多数对于液力透平导叶的研究仅针对于首级导叶，对多级液力透平级间导叶的研究较少。为研究级间导叶对多级水轮机模式液力透平的性能影响，本文以一台二级水轮机模式液力透平为研究对象，选取导叶数不同的五种新型空间导叶，分析导叶数对水轮机模式液力透平的水力特性和压力脉动影响，为多级水轮机模式液力透平级间导叶的优化提供参考。

1 液力透平的主要参数

本文选取一种以超低比转速混流式转轮为的二级液力透平进行研究，其中两级转轮结构相同，进水室采用蜗壳进水室，首级导叶选取径向导叶，级间导叶采用新型空间导叶，具体如图1 所示；出水室采用环形出水室；部件的基本参数如表1 所示，液力透平结构具体如图2所示。

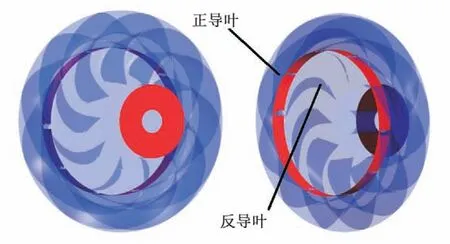
图1 新型空间导叶结构图Fig.1 Structure of new space guide vane

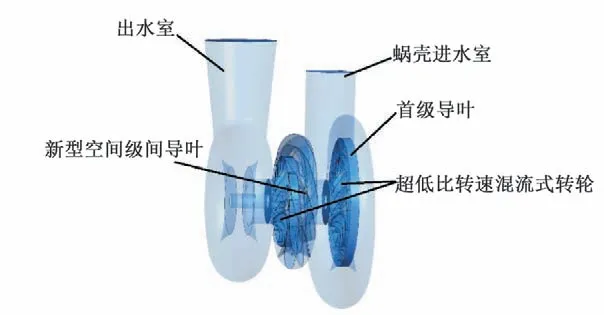
图2 T模式液力透平Fig.2 T-type hydraulic turbine

表1 各部件设计参数Tab.1 Design parameters of various components

2 定常计算

2.1 网格划分与数值模拟计算

基于ICEM，采用非结构化网格中八叉树的方法对液力透平三维模型进行网格划分。同时，保证网格质量在0.3 以上，对模型进行网格无关性验证，当网格数在550 万个左右时，效率和水头浮动均在0.5%以内，具体如图3所示。

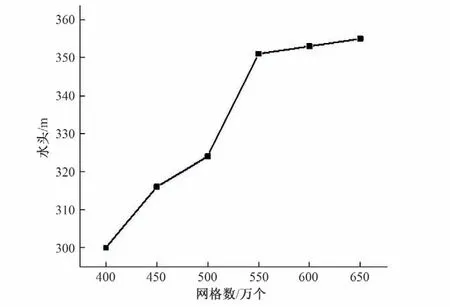
图3 计算域网格划分无关性验证Fig.3 Verification of grid independence in computational domain

数值模拟方面，运用CFD-fluent 软件对模型进行全流道定常计算，数值计算求解方法采用有限体积法，假设为不可压缩三维流动，且满足连续性方程和动量方程，选用标准k-ε湍流模型，收敛精度设为10-4。液力透平进口边界设置为速度进口，出口设置为无压力出口，所有壁面的边界条件选择为wall，设置为固定壁面，满足无滑移条件，各部件交界面设置为interface。

2.2 实验验证

为了验证数值计算的准确性，对采用新型空间导叶数为10的模型进行性能实验，具体试验示意图如图4 所示。实验结果如图5 显示，可以看出，试验和数值模拟得到性能曲线趋势一致，由于数值模拟没有考虑机械损失，还忽略了平衡孔泄露损失，所以计算结果偏大。在最高效率点，采用相对误差值计算，水头误差为3.1%，效率误差为6.57%，可见本文所采用的数值计算方法能较好的预测透平性能。

图4 液力透平试验台Fig.4 Hydraulic turbine test bench

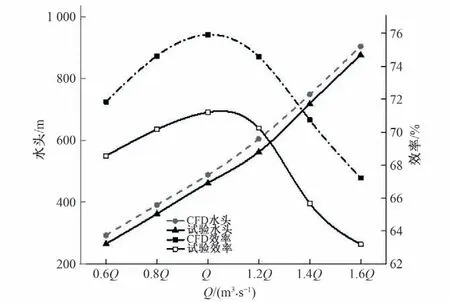
图5 效率最优的模型透平试验外特性和数值模拟外特性对比Fig.5 Comparison of external characteristics of model turbine test and numerical simulation with optimal efficiency

2.3 流量-效率、流量-可利用水头外特性分析

选取导叶数分别6、8、10、12、13 的新型空间导叶，通过CFD-fluent 计算得到在0.6Q、0.8Q、Q、1.2Q、1.4Q、1.6Q工况下，得到整个T 模式液力透平的效率和可利用水头变化如图6所示。

如图6所示，随着导叶数的增加，液力透平效率先增大后减小，在导叶数为12 时，效率最高。同时，5 种不同导叶数下，液力透平均在额定工况处达到效率最高。转轮和新型空间导叶损失计算结果如图7显示，新型空间导叶数增加，转轮的水头损失下降。因此分析原因为随着导叶数增加，导叶对水流的导控能力增强，导叶间水流流态变好，导叶和转轮的损失都逐渐减小，但当数量达到一定数时，导叶的摩擦损失增加，损失开始增大，效率有所降低。同时导叶数增加，总可利用水头均呈现增加趋势，原因为导叶数增加，导叶摩擦损失和整个装置的总可利用水头也逐渐增加。

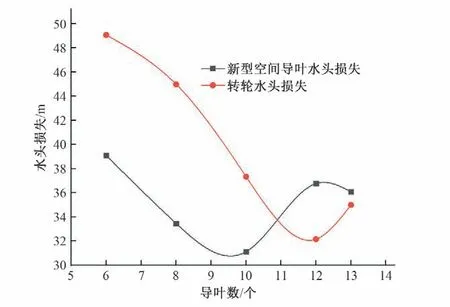
图7 新型空间导叶和转轮水头损失Fig.7 Head loss of new space guide vane and runner

2.4 内部流态

外特性中可利用水头和效率的变化是由内部流态的变化引起的，导叶数变化会引起导叶内静态压力，流线等内部能量特性发生变化，静态压力越大，对应的能量损失以越大，内部流态稳定性就越小；流线直接反映出液流在流道中的流态好坏。

2.4.1 新型空间导叶内部静压力特性分析

对于五种方案进行定常计算，得到压力云图如图8 所示。随着导叶数的增加，压力逐步上升，反导叶高压区范围扩大，从导叶数为10 开始，高压区延伸到过渡段和正导叶处，随后呈梯度减小，在正导叶出口处压力降到最低。但对所接转轮的内部压力分布几乎没有影响，分析原因可能为导叶数增加，导叶导控能力增加，液体所流流道面积减小，流速增加，压力上升，这与导叶数增加可利用水头增加的规律相符。

图8 不同导叶数压力云图Fig.8 Pressure nephogram with different number of guide vanes

2.4.2 流线分布

对于5 种方案进行定常计算，得到不同导叶数内部流线图如图9 所示。导叶数增加，对新型空间导叶内部流态没有显著影响，除导叶数为12 和13 时反导叶处出现少量漩涡，其余无明显区别，但对所接转轮中内部流态影响显著。导叶数增加，所接转轮内部流线逐渐变好，导叶数最高13 时，转轮进口几乎没有涡流，原因为导叶数增加，控制液流能力增强，使之更能够以符合转轮所需液流方向进入下级转轮。

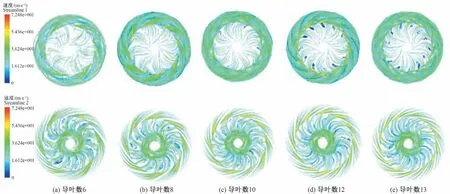
图9 不同导叶数内部流线分布Fig.9 Internal streamline distribution with different number of guide vanes

3 压力脉动分析

3.1 监测点布置及计算设置

透平内部的压力脉动是造成装置振动的主要因素之一，而透平内部的压力脉动主要是由过流部件之间的动静干涉产生的。数值结果显示，转轮和级间导叶的损失占到整体损失的50%以上，为了研究不同级间导叶数对透平内部压力脉动的影响，本文选取两级转轮和新型空间导叶作为脉动研究对象，分别在首级转轮，二级转轮和新型空间导级间导叶内布置压力监测点，并在额定流量工况下进行非定常计算，具体压力监测点的布置方式如图10所示。

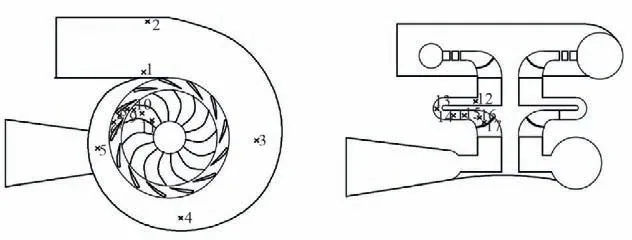
图10 监测点的选取Fig.10 Selection of monitoring points

为了消除静压对结果的干扰，引入压力系数Cp对压力脉动结果进行分析。Cp表达式如下：

式中：P为瞬时压力为采用时间内的平均压力；ρ为液体密度；U为叶轮出口圆周速度。

3.2 转轮内压力脉动分析

3.2.1 一级转轮内部压力脉动

通过数值计算得到不同级间导叶数下一级转轮内部压力脉动频域图和最大脉动压力值表如图11 和表2 所示。可以看出，不同导叶数下，沿着流动方向，监测点压力脉动主频幅值均呈现减小的趋势，越靠近转轮出口，幅值越小，这是因为在进口接近耦合面，动静干涉较为强烈，越远离进口所受动静干涉越小。同时，随着导叶数增加，一级转轮内部进出口压力脉动变化幅值不明显，但有增大趋势，靠近进口处的监测点9和靠近出口处的监测点11 主频幅值均增加，这是因为级间导叶数增多，反导叶进口处过流面积越小，导叶进口处流道内流速增大，一级转轮所受的动静干涉也就越强烈，主频幅值随之增加。

图11 一级转轮内压力脉动频域图Fig.11 Frequency domain diagram of pressure fluctuation in primary runner

表2 一级转轮内最大脉动压力值 kPaTab.2 Maximum pulsating pressure value in the primary runner

3.2.2 二级转轮内部压力脉动

通过数值计算得到二级转轮内部压力脉动频域图和最大脉动压力值表如图12 和表3 所示。可以看出，不同新型空间导叶数下，沿流动方向，压力脉动主频幅值和最大脉动幅值均呈现减小趋势。原因为二级转轮进口处与级间导叶连接，级间导叶和转轮动静干涉，产生的压力脉动幅值变大，距离进口越远，受干涉强度越小，压力脉动幅值也就越小。还可以看出，随着新型空间导叶数的增加，转轮进口处的脉动幅值总体为减小趋势，说明级间导叶数增加，正导叶内流道减小，级间导叶内对束流能力增强，对应图9 可以看出，随着级间导叶数增加，二级转轮进口的液力流态变好，从而转轮进口处脉动幅值减小；同时，二级转轮出口的主频幅值和最大脉动幅值变化不明显，级间导叶数对二级转轮的影响主要体现在转轮进口处，可见，适当增加导叶数可以减小二级转轮进口处压力脉动幅值。

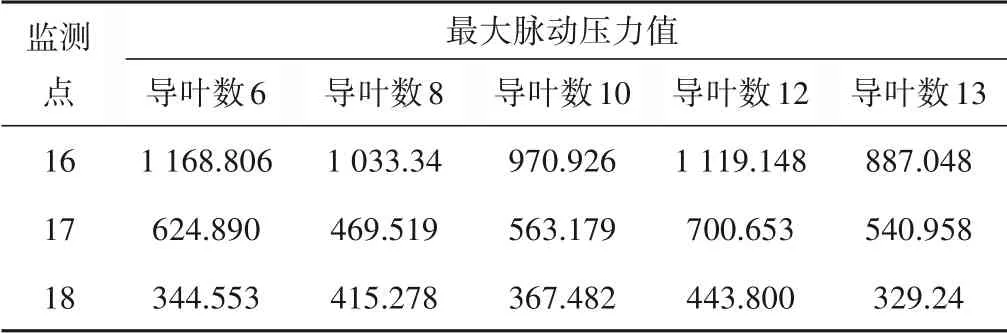
表3 二级转轮内最大脉动压力值 kPaTab.3 Maximum pulsating pressure value in the secondary runner

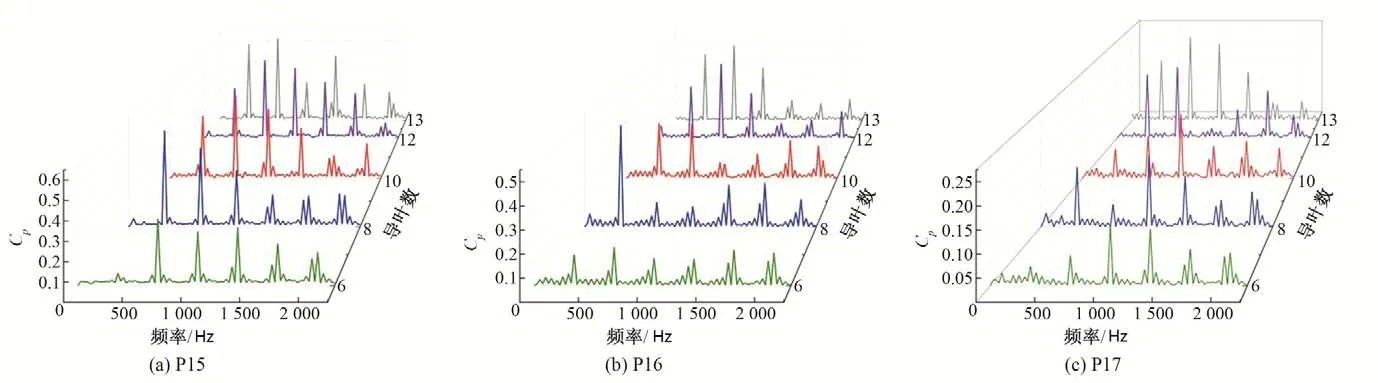
图12 二级转轮内压力脉动频域图Fig.12 Frequency domain diagram of pressure fluctuation in secondary runner

同时，对比一级转轮内部脉动幅值变化，级间导叶数增加，对二级转轮内部压力脉动幅影响更为显著。

3.3 级间导叶压力脉动分析

图13 为将数值计算进行傅里叶变换得到的级间导叶内各检测点的压力脉动频域图，表4为通过数值计算的方法得到级间导叶内各检测点处的最大脉动压力值。

结合图13 和表4 可以看出，不同级间导叶数下，沿液体流动方向，压力脉动主频幅值均逐渐减小，但级间导叶数增加，反导叶进口和正导叶出口处的压力脉动主频幅值均增大，因为导叶数增加，流道面积减小，流道内流速和压力值上升，结合图8压力云图可以看出，正导叶和反导叶处压力值上升，脉动强度也跟着上升，可以看出，导叶数为8 时，正导叶导叶出口处脉动幅值最小，但是反导叶进口处脉动幅值大，导叶数为10时，反导叶进口处压力脉动幅值最小，且正导叶出口处仅比导叶数为8时脉动幅值打，可见，在一定参数范围内，适当增加导叶数能降低导叶内部自身的压力脉动幅值。

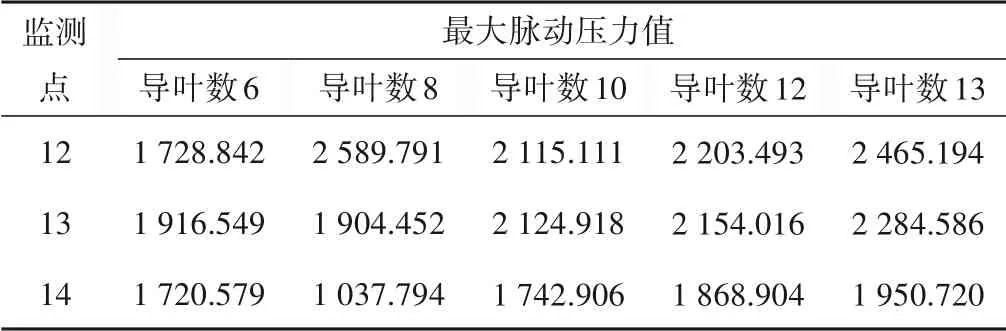
表4 级间导叶内最大脉动压力值 kPaTab.4 Maximum pulsating pressure value in the interstage guide vane

图13 级间导叶内压力脉动频域图Fig.13 Frequency domain diagram of pressure fluctuation in interstage guide vane

4 结 论

（1）新型空间级间导叶数增加，整个T模式液力透平效率先增加后减小，最高效率出现在导叶数为12 时；可利用水头为逐渐增加的趋势；不同流量工况下，导叶数增加，效率也为先增大后减小，可利用水头逐渐增加，五种模型的最优效率和可利用水头均出现在额定工况附近。

（2）新型空间导叶数增加，导叶内部静态压力值，流线均发生变化。导叶数增多，正导叶处逐渐出现高压区，反导叶处高压区面积增大；同时，级间导叶数增加所接转轮进口流线变优，但是反导叶处出现漩涡，当导叶数为12 时，静压和流态处于较优状态。

（3）新型空间导叶数增加，一级转轮内部脉动幅值增加、二级转轮内部压力脉动主频幅值减小，新型空间导叶自身内部压力脉动幅值增加。但是一级转轮和导叶内部脉动幅值增加幅度小于二级转轮内部脉动减小幅值，因此，在一定透平结构参数下，适当的增加新型空间导叶数能减小透平内部压力脉动幅值。

（4）综合上述研究可知，级间导叶数对水轮机式多级液力透平水力性能和压力脉动特性影响较大，综合其水力特性和压力脉动特性，对于本文中的液力透平，推荐最佳级间导叶数为12。