电磁炮炮管振动信号分析及处理方法*

赵 辉，郭利强，兰国峰，郝慧艳，程日炜

（1.中北大学信息与通信工程学院，太原 030051；2.上海航天技术研究院北京研发中心，北京 100081）

0 引言

电磁炮发射时会产生强烈振动，同时，电枢在轨道内高速运动时由于与轨道摩擦、碰撞也会产生剧烈的振动［1-4］，严重影响电磁炮的发射精度和稳定性。因此，在电磁炮研发阶段有必要对其炮管振动情况进行分析、研究，从而为进一步优化炮架、炮管及其固定和减振结构提供数据支持，以改善和提高电磁炮发射精度及稳定性。

目前，国内外常用测量方法主要有：光电位移测量法和加速度传感器测量法［5-6］，光电位移测量法常用于测量炮管出口位置的振动情况，精度较高；而加速度传感器测量法不仅能够测量炮口位置振动情况，而且能够测量炮身任何位置的振动情况，由于电磁炮发射和结构特点，根据测量需求，在满足测量精度要求的情况下，本文选择采用加速度传感器对炮管振动信号进行采集。

通过实验及数据分析，发现加速度传感器采集到的信号除炮管振动信号外，还有很多干扰信号，而在计算炮管振动位移参数时，干扰信号会使位移信号发生畸变，给测量结果带来很大误差。为了解决这一问题，需要对采集到的信号进行处理，目前，主要处理方法有：基于傅里叶变换的频谱分析法、基于小波变换的小波阈值去噪法及最小二乘法等，频谱分析法主要用于处理周期性明显的相对平稳信号，小波阈值去噪法适合对非平稳随机信号进行处理，而最小二乘法适用于变化缓慢、无明显周期性信号。本文将对电磁炮炮管结构、振动情况及相应信号特点和信号处理方法进行分析、研究，选用合适的信号处理方法，并进行相应实验，得到炮管振动数据参数，验证该信号处理方法的有效性，为电磁炮设计、优化提供可靠的数据支持。

1 炮管振动信号分析

电磁炮是通过电磁力作用于电枢进行发射的一种新型武器，具有电枢发射速度快、冲击力强，炮体结构复杂、炮管长、质量大等特点。炮体主要由发射身管（炮管）和发射架（炮架）两部分组成，两者之间通过复杂机械结构进行连接。根据其结构特点，理想条件下，炮管可简化为一端固定的悬臂梁，其受力示意图如图1 所示。在电磁发射过程中，电枢在炮管内高速运动，炮管在运动电枢及自身重力的激励下产生振动，根据悬臂梁振动特性，炮管振动呈现刚性阻尼运动规律［7］，即炮管振动是一随时间变化的往复过程，且振动幅值由大缓慢减小，最终回到初始位置。

图1 电磁炮炮管受力情况示意图

由于测试环境较复杂，使用加速度传感器采集到的电磁炮炮管振动信号不但包含炮管振动有效信号，还包含有许多干扰信号，根据电磁炮结构和采集到的信号特点，可以将其信号分为以下4 种：1）炮管振动有效信号：炮管振动信号，该信号主要呈现刚性阻尼运动规律，信号频率低、周期长；2）电枢扰动干扰信号：由电枢高速加速运动，与轨道发生摩擦、振动，产生的扰动干扰信号，其信号特点是频率高、幅值高、周期短；3）传感器与炮管共振干扰信号：传感器与炮管刚性连接，发射过程中，传感器与炮管共振产生的干扰信号，其信号特点是频率高、幅值低、周期短；4）传感器漂移噪声：电磁炮发射过程中，伴随在测试点产生温度变化，使传感器受到影响，引起噪声，其信号特点是变化缓慢、幅值低。

炮管振动测试中，传感器采集到的信号是炮管振动有效信号与多种干扰信号混合后的复杂信号。因此，需根据不同信号特点，采用合适的信号处理方法，对其进行处理，最后得到炮管振动有效信号。

2 信号处理方法研究

2.1 电枢扰动、传感器共振干扰信号去除方法

通过第1 节分析可知，电枢扰动和传感器共振干扰信号相较于炮管振动有效信号具有频率高、周期短的特点，因此，在去除这两种干扰信号时，首先应在信号的时域及频域上同时对其进行分析，再采用合适的方法对炮管振动有效信号进行提取。

小波变换具有良好的时频特性，能够根据信号频率成分，调整窗口，在抑制干扰信号的同时，保留有效信号，包括有效信号中的细节信息［8-9］。因此，采用基于小波变换原理的小波阈值去噪方法能够对干扰信号进行分析，并实现炮管振动有效信号提取。

图2 小波阈值去噪方法示意图

接下来，通过选取合适的阈值规则来处理小波系数，得到估计小波系数。本文采用Minimax 准则来确定阈值的大小，选择规则为：

式（4）中，n 为待计算小波系数的长度，σ 为噪声信号的标准差。

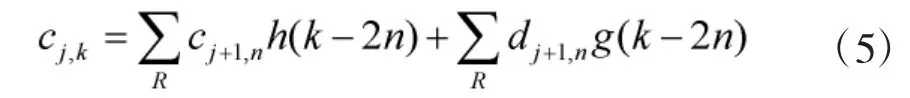
最后，根据式（5）进行信号重构，获得炮管振动有效信号。

2.2 传感器漂移噪声去除方法

由于传感器在测试过程中会受到温度变化影响，信号产生温漂，而积分计算又具有累加特性，会使采用积分计算求取的振动位移信号产生很大误差，因此，需要采用合适的方法去除传感器漂移噪声干扰信号，以提高测试精度和准确性。

最小二乘法是一种误差估计计算方法，能通过线性拟合计算得到信号中的多项式趋势项，即漂移干扰信号，将其去除即可得到无漂移干扰信号。

处理方法：令原始信号为xk，用m 阶多项式yk对xk拟合，并使xk和yk间的差的平方和E 最小：

将E 依次对多项式yk的系数a 取偏导，得到m+1 个方程组，如式（8）：

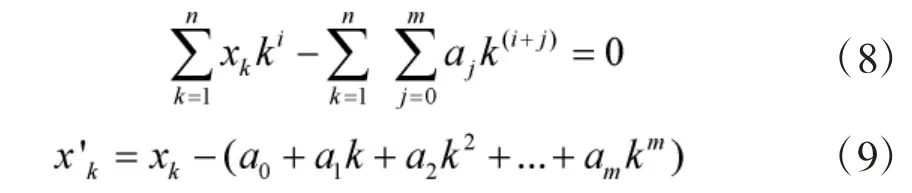
求解式（8），得到漂移干扰信号，最后采用式（9）去除干扰信号，得到无漂移干扰的有效信号。

3 炮管振动信号模拟仿真及信号处理

通过对炮管振动信号分析可知，有效信号呈现刚性阻尼运动规律，干扰信号无固定规律，为随机信号。因此，本节将采用Matlab 软件模拟采集到的振动信号，其中：图3（a）、图3（b）分别为炮管理想模拟振动信号（无干扰的理想振动信号）和加入随机噪声的振动信号。使用第2 节所述的小波阈值去噪方法进行信号处理，验证该方法的有效性和可靠性。

图3 炮管模拟振动信号

小波阈值去噪方法中，如何在常用小波基Haar、Daubechies、Symlets 小波中选取合适的小波基很关键。为确定适合炮管振动信号处理的最佳小波基，引入均方根误差指标，对模拟振动信号处理效果进行评价。式（10）为均方根误差（RMSE）表达式，其数值越小，表明采用该小波基去噪效果越好。

表1 为炮管模拟振动信号在信噪比为20dB～40 dB的情况下，采用不同小波基进行处理后的效果。从表1 可看出，Daubechies 小波相较于另外两种小波，其RMSE 值最小，去噪效果最好，因此，采用Daubechies小波对电磁炮炮管振动信号进行处理更加适合。

表1 不同小波基去噪效果比对数据

电磁发射过程中，炮管振动位移量是振动测试中非常重要的一个参量。要获得振动位移量，首先要将加速度传感器采集的振动信号进行去噪处理，获得加速度参量，再通过二次积分得到振动位移参量。

式（11）为传感器电压值与加速度值映射关系：其中，传感器的灵敏度为0.01v/g，Acc 为加速度值，v为传感器输出电压，g 为重力加速度。

表2 为炮管理想模拟振动信号位移量和含噪声的振动信号经信号处理后得到的位移量之间的比对数据。

表2 振动信号位移量比对数据

从表2 可以看出，在20 dB～40 dB 信噪比下，含噪声的振动信号经信号处理后，得到的位移量相较于理想振动信号位移量误差较小，表明所采用的小波阈值去噪方法，能够有效去除电磁炮炮管振动干扰信号，得到有效振动信号。

4 实测实验数据处理与分析

为了进一步验证炮管振动信号处理方法的有效性，本文设计了振动测试系统对电磁炮振动信号进行了实测，测试系统组成原理图如图4 所示。

图4 测试系统组成原理图

当电磁炮发射时，三轴加速度传感器测得炮管待测点X、Y、Z 3 个方向的加速度信号，经过信号调理装置后，由数据采集装置送入计算机完成信号采集和处理。传感器和炮管采用刚性结构连接，实验现场传感器安装图如图5 所示，其中：三轴传感器X 轴为电枢运动方向，Y 轴为炮管左右方向，Z 轴为炮管上下方向。

图5 实验现场传感器安装图

本节将采用第2 节所述的信号处理方法，对实测实验所采集到的实验数据进行处理和分析。

4.1 实验数据频谱分析

通过加速度传感器采集到的X 方向原始信号如图6（a）所示，可以看出，信号非常复杂，含有大量的干扰信号。由第1 节信号分析可知，有效信号和干扰信号的振动频率不同。因此，需要将原始信号进行傅里叶变换，在频域上对其进行分析。傅里叶变换关系式为：

图6 X 方向原始信号及其频谱图

图6（b）为将原始信号进行傅里叶变换后的信号频谱图。由图可知，原始信号主要在0 kHz～1 kHz、4 kHz～6 kHz 及30 kHz～35 kHz 频段内，其中，0 kHz～1 kHz 频段内的能量最高，根据炮管振动有效信号的特点，可知该频段内信号应为振动有效信号。电枢扰动干扰信号和传感器共振干扰信号均具有频率高、周期短的特点，但电枢扰动干扰信号较传感器共振干扰信号幅值高。因此，可得出4 kHz～6 kHz 频段内的信号应为电枢扰动干扰信号，30 kHz～35 kHz 频段内的信号应为传感器共振干扰信号。

4.2 电枢扰动和传感器共振干扰信号的去除

为了去除炮管振动信号中的干扰信号，通过对实验数据进行频谱分析，在得到有效信号所在频段的基础上，将采用小波阈值去噪方法对电枢扰动和传感器共振干扰信号进行去除。

采集的原始信号如图7（a）所示，利用Dau-bechies小波进行离散小波变换，可得到图7（b）～图7（h）所示的不同分解尺度下的各层细节信息，可以看出，对原始信号进行7 层分解之后，可分离出大部分炮管振动有效信号。

图7 X 方向炮管振动信号分解图

接下来，为获得信号重构所需的估计小波系数，利用Minimax 准则来确定阈值函数，保留小波变换系数中高于阈值的部分，再通过信号重构，得到炮管振动有效信号，如图8（a）所示。再对其进行傅里叶变换后得到其频谱图，如图8（b）所示，可以看出，提取的炮管振动有效信号集中在0 kHz～1 kHz频段内，其他频段的干扰信号均被去除，且有效信号呈阻尼运动规律。

图8 X 方向炮管振动有效信号及其频谱图

4.3 传感器漂移噪声的去除

从图8（a）中可以看出，振动信号末端未归零，存在信号漂移现象，因此，采用最小二乘法对去除干扰信号后的振动有效信号进行处理，处理结果如图9 所示，从图中可看出，信号末端归零，漂移噪声已去除。

图9 X 方向去除漂移噪声后振动有效信号图

4.4 Y 方向和Z 方向信号分析和处理

实验中，传感器采集到的Y 方向和Z 方向原始信号如下页图10（a）、图11（a）所示，原始信号中同样存在着大量的干扰信号，同理，采用X 方向原始信号分析、处理方法，对Y 方向和Z 方向原始信号分别进行分析和处理，即可得到Y、Z 方向炮管振动有效信号，如图10（b）、图11（b）所示。

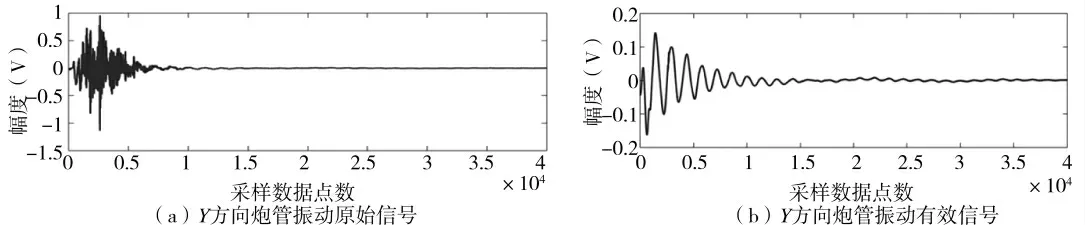
图10 Y 方向炮管振动信号

图11 Z 方向炮管振动信号

4.5 炮管振动位移参量分析

将三轴加速度传感器输出电压值通过映射关系式（11）计算得到相应加速度值，再进行二次积分，即可得到发射过程中炮管在各个方向的振动位移量。图12 所示为炮管振动三维运动曲线，其中，X、Y、Z方向所对应的位移最大值分别为17.5×10-3m、0.79×10-3m、0.26×10-3m。图12 中箭头所示方向为振动开始方向，振动由0 点位置开始，沿右上方振动一周后，回到0 点位置，满足阻尼运动规律。

图12 炮管振动三维运动曲线

5 结论

本文针对电磁炮炮管振动参数测试过程中，传感器采集到的信号存在很多干扰，需要采用合适的方法进行信号处理，从而准确获取炮管振动有效信号这一问题进行分析和研究。首先对炮管振动信号进行了分析，得到振动有效信号及各干扰信号特点；然后根据各信号特点对信号处理方法进行了研究，得到了采用小波阈值去噪和最小二乘法相结合的方法来去除振动干扰信号的信号处理方法，并通过模拟仿真原始信号，对信号处理方法进行验证；最后设计了振动测试系统，对电磁炮振动信号进行了实测，并采用本文所述信号处理方法对实测数据进行了分析、处理，较好地得到了炮管振动有效信号，进一步验证了该信号处理方法的有效性和实用性；在此基础上，对振动有效信号进行分析、计算，得到了炮管振动位移参量，为电磁炮设计、优化、定型提供了数据支撑和理论依据。