非组合模型下Galileo 双频与三频短基线解算精度分析

徐亚楠，刘舜

(1.广州番禺职业技术学院，广州 511483；2.陕西铁路工程职业技术学院，陕西 渭南 714099)

0 引 言

全球导航卫星系统(GNSS)以北斗卫星导航系统(BDS)、GPS、Galileo 和GLONASS 四大系统为主，当前每个系统都能单独提供全球定位服务，且部分卫星能播发三频甚至三频以上的信号，为GNSS 精密数据处理提供了新思路[1-3].Galileo 系统是欧盟建设和研发的卫星导航定位系统，于2016 年12 月15 日正式声明公开服务，其建设计划最早可追溯到20 世纪90 年代，该系统计划由30 颗卫星组成，且能播发E1、E5a、E5b 等多频信号[4-7].虽然Galileo 系统正式开通服务时间较短，但国内很多学者对其定位性能进行了研究.文献[8]基于多个MGEX(Multi-GNSS Experiment)跟踪站数据分析校正天线参数对Galileo系统双频精密单点定位(PPP)的影响，研究结果表明，与消电离层定位结果相比，水平定位精度相当，高程方向定位精度提升较大.文献[9]推导了适用于多频非组合(UC)观测值的GNSS 卫星精密定轨模型，并且基于多测站Galileo 双频和三频数据进行定轨，发现双频UC 模型与IF 模型定轨精度相当，三频UC模型和IF 模型浮点解精度较E1/E5b 双频组合结果有一定的提升.文献[10]对比分析了Galileo 系统双频无电离层组合、双频非差非组合和三频非差非组合PPP 精度以及收敛时间，发现Galileo 三频PPP精度较优，且相比双频PPP 精度有明显提升，但较收敛时间的提升并不明显.文献[11]利用非组合模型解算了Galileo 系统三频组合PPP 精度，发现三频PPP精度与收敛时间优于传统双频PPP，尤其是在观测数据异常时效果更为明显.文献[12]分析了GPS/Galileo组合PPP 精度，发现双系统组合PPP 具有较好的定位结果，且定位精度与收敛时间较单系统具有一定的改善.综合当前各学者对Galileo 系统研究的内容与方法，本文基于自测试9 km 短基线，提出利用一种UC 定位模型解算Galileo 双频与三频短基线数据，并且进一步分析了不同频率组合下定位精度.

1 数学模型

在短基线定位中，双差函数模型是常用的解算模型.该模型能有效消除接收机钟差、卫星钟差，可以最大程度地削弱电离层延迟、对流层延迟和卫星轨道误差的影响，有利于模糊度的固定[13].双差载波相位与伪距观测方程[14]一般表示如下：

在利用UC 模型定位时，电离层误差无法消除，因此将电离层误差当作未知参数进行估计，在式(1)的基础上可以进一步得到三频非组合短基线定位模型[11,15-16]，表示如下：

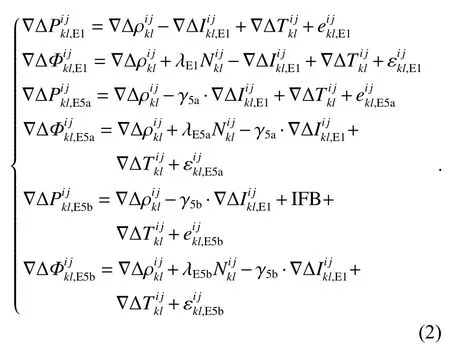
式中：I FB 为频间偏差；γ 为不同频率间的电离层因子；其余符号表示含义与之前相同.

在式(1)、(2)的基础上进一步利用卡尔曼滤波进行参数估计，利用LAMBDA 算法进行模糊度固定，最终解算得到接收机坐标.

2 数据解算分析

为详细评估非组合模型下Galileo 系统双频与三频短基线解算性能，试验设计了一条约9 km长的短基线，数据采集时高度截止角设置为12°，采集时间为2020 年3 月12 日全天，采集间隔为30 s，接收机类型为TRIMBLE ALLOY，天线类型为TRM59800.00.

数据解算软件为根据RTKLIB 编译的开源程序，以GAMIT 软件解算得到的静态坐标作为参考坐标，对流层改正模型采用Saastamoinen 模型，其他误差通过对应模型进行改正.在进行数据解算时，首先解算得到Galileo 系统E1/E5a、E1/E5b 以及E5a/E5b 双频组合短基线定位结果，然后解算得到E1/E5a/E5b 三频组合短基线定位结果，最后根据解算得到的定位结果与参考坐标计算得到定位偏差与定位精度.

如图1 所示，给出了Galileo 系统的卫星可用数与位置精度因子(PDOP)值随时间变化情况.由图1可知，在整个观测期内，Galileo 系统的卫星可用数为4～9 颗，平均卫星可用数为6 颗.Galileo 系统的PDOP 值除个别历元外，PDOP 值在4 cm 以内，平均PDOP 值为2.13 cm.如图2 所示，给出了Galileo 系统双频与三频解算历元率，由图2 可知，Galileo 系统双频与三频短基线历元解算率都在95%以上，三种双频历元解算率相当，而三频历元解算率较双频有一定提升.

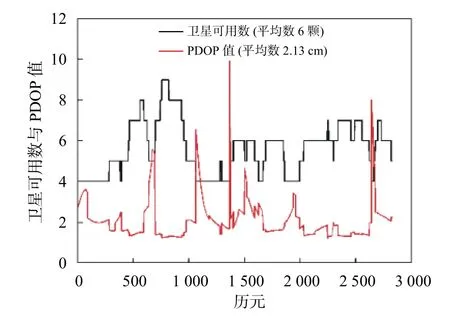
图1 卫星可用数与PDOP 值

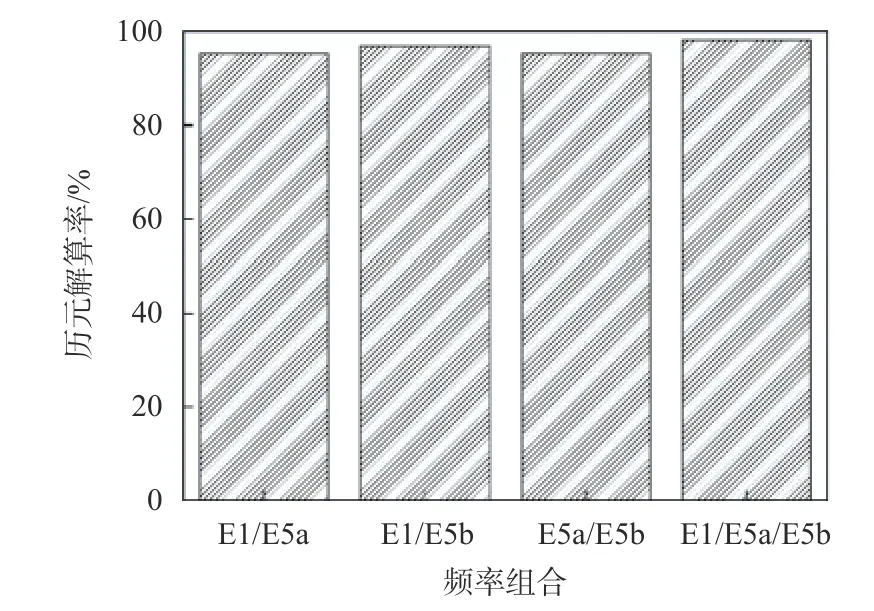
图2 历元解算率

根据解算得到坐标与参考坐标，计算得到水平方向与高程方向的定位误差，Galileo 系统双频与三频水平向与高程向定位误差，如图3～图6 所示.

由图3～图5 可知，E1/E5a 和E5a/E5b 组合短基线定位E 方向定位误差小于0.4 m，N 方向定位误差小于0.3 m，U 方向定位误差小于0.6 m，E1/E5b 组合短基线定位E 方向定位误差小于0.3 m，N 方向定位误差小于0.3 m，U 方向定位误差小于0.6 m.由图6可知，Galileo 三频短基线定位误差较双频有所减小，E 方向定位误差小于0.3 m，N 方向定位误差小于0.3 m，U 方向定位误差小于0.4 m.

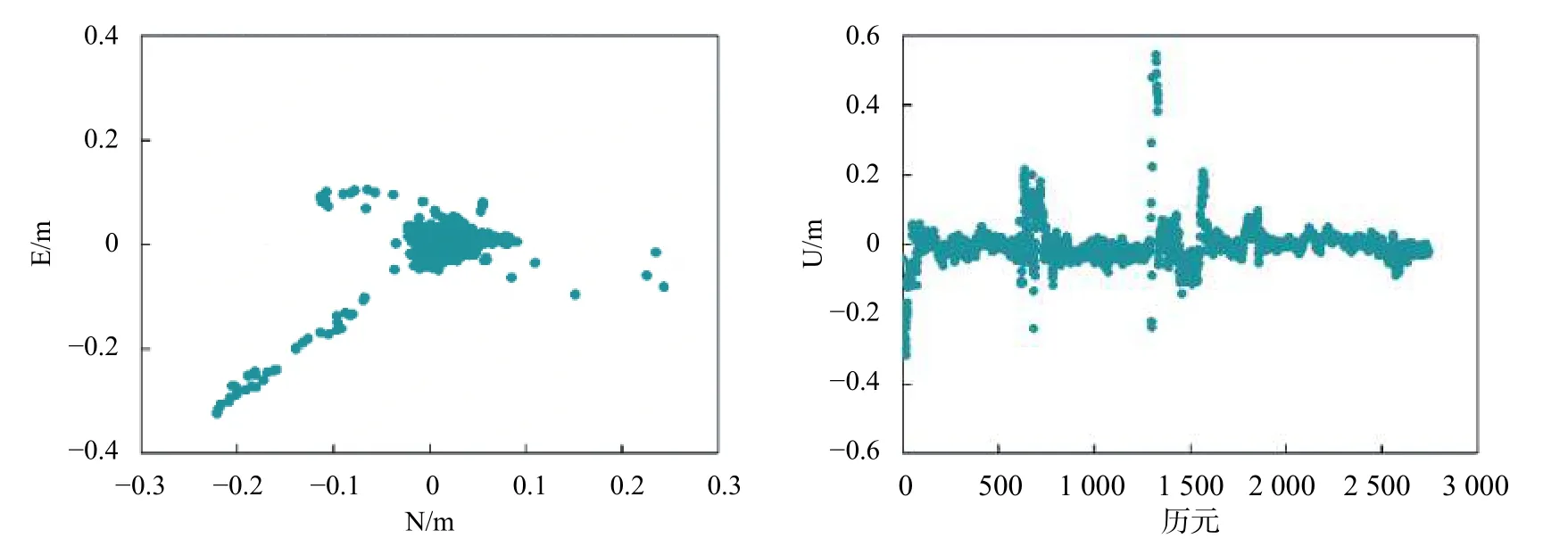
图3 E1/E5a 组合短基线水平与高程向定位误差

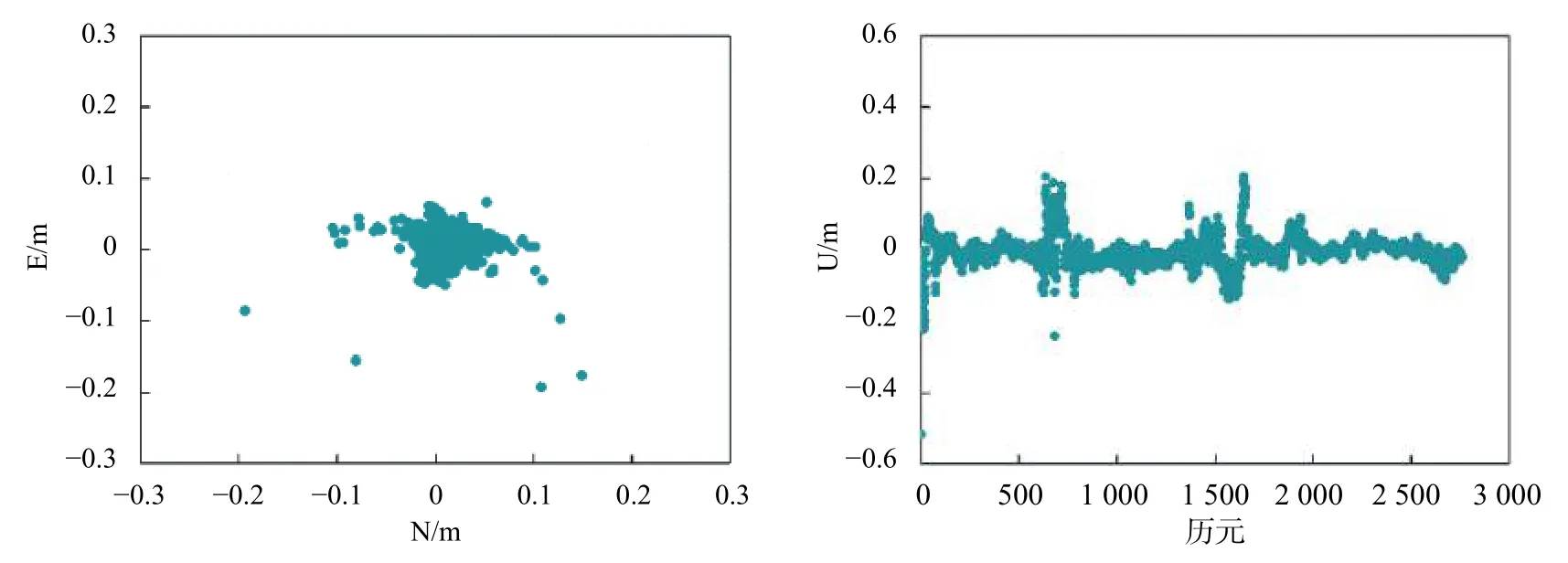
图4 E1/E5b 组合短基线水平与高程向定位误差

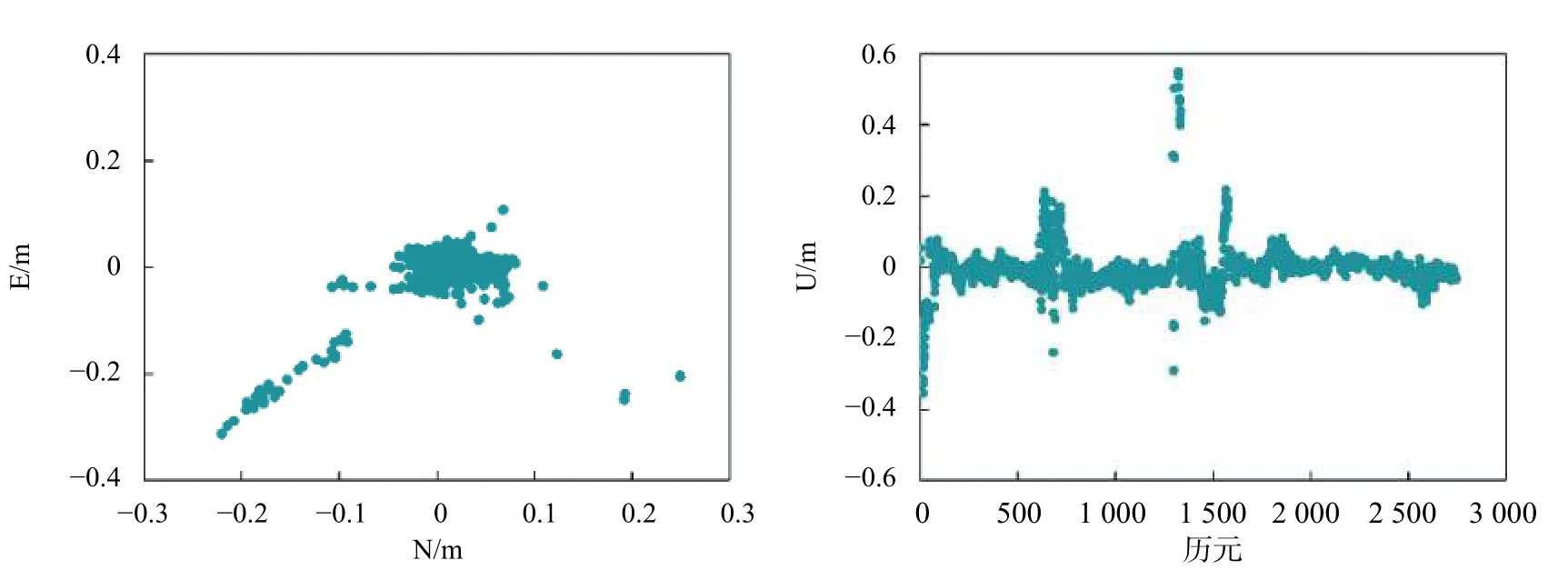
图5 E5a/E5b 组合短基线水平与高程向定位误差

图6 E1/E5a/E5b 组合短基线水平与高程向定位误差

为进一步直观的表示Galileo 双频、三频定位精度以及三频较双频短基线定位精度的提升，统计了不同频率组合东(E)、北(N)、天(U)三个方向的定位精度以及三频较双频短基线定位精度的提升量，如表1所示.

表1 Galileo 双频与三频短基线基线解算精度均方根(RMS)及三频较双频定位精度提升统计

由表1 可知，E1/E5a 和E5a/E5b 短基线E 方向和U 方向定位精度相当，E 方向定位精度优于3.5 cm，U 方向定位精度优于9 cm，E1/E5a 组合N 方向定位精度优于5 cm，E5a/E5b 组合N 方向定位精度优于4 cm，E1/E5b 组合定位精度优于E1/E5a 和E5a/E5b，E 方向定位精度优于2 cm，N 方向定位精度优于4.5 cm，U 方向定位精度优于5 cm.E1/E5a/E5b 三频组合短基线定位精度优于任一双频组合，E 方向定位精度优于1.5 cm，N 方向定位精度优于2.5 cm，U 方向定位精度优于3.5 cm.同时发现，三频组合短基线定位精度较双频定位精度有明显提升，提升量在30%～60%.

3 结束语

本文基于9 km 短基线实测数据，分析了非组合模型下Galileo 双频与三频短基线解算精度，结果表明，Galileo 卫星可用数和PDOP 值较优，双频历元解算率相当，三频历元解算率较双频有明显提升.双频短基线定位中，E1/E5b 组合定位精度要优于另外两种双频组合定位精度，但是定位精度都在cm 级，水平定位精度优于5 cm，高程精度优于10 cm.三频组合短基线定位精度较双频组合有明显提升，E 方向定位精度优于1.5 cm，N 方向定位精度优于2.5 cm，U 方向定位精度优于3.5 cm.