改进的函数连接型非线性回声对消算法

2021-08-07王仁杰杨晓敏芦璐

现代计算机 2021年17期

王仁杰，杨晓敏，芦璐

(四川大学电子信息学院，成都 610065)

0 引言

近年来，通信和网络技术不断发展，使得人们对通信的质量提出了新的要求，其中最主要的就是语音通话质量。声学回声是降低语音通话质量的重要因素之一[1]。回声是由于麦克风和扬声器之间的回声路径的脉冲响应耦合效应而产生的。由于人耳对回声非常敏感，延迟超过10ms的回声就能被人耳捕捉到，超过32ms的回声就会严重干扰通话质量。因此，如何消除声学回声具有重要的现实意义。目前最普遍应用的方法是基于自适应滤波的回声消除器(Acoustic Echo Cancellation，AEC)。AEC的基本原理是运用自适应滤波算法对回声路径的脉冲响应进行估计，其本质是一个系统辨识的问题。然而当回声路径存在非线性的特性时，传统的自适应滤波算法，比如最小均方算法(Least Mean Square，LMS)、归一化最小均方算法(Normalized Least Mean Square，NLMS)的性能会出现明显的下降。因此，如何对回声路径中的非线性特性建模，提出有效的非线性回声对消方法具有重要意义[4]。

目前的非线性回声对消的方法中，具有代表性的有以下两种。文献[1]中提出了一中基于函数连接的非线性自适应滤波算法用于回声对消(Split Functional Link Adaptive Filter，SFLAF)。该方法的特点是对输入信号进行非线性扩展，具体地说，是通过三角函数函数连接扩展，将未经过变换的信号和经过变换的信号分别用两个滤波器进行滤波，以此达到同时对回声路径的线性和非线性特性建模的目的。文献[2]将回声路径中的非线性变换设定为一种sigmoid变换，在进行滤波之前对sigmoid的参数进行估计，并结合RLS的快速收敛和强跟踪能力，能快速使得估计值收敛到真实值。

受以上方法的启发，本文结合以上两种方法，对函数连接型自适应回声对消器做出改进：其中在文献[1]中的SFLAF的线性滤波器中引入文献[2]的RLS-sigmoid算法，将回声路径中的非线性变换设定为sigmoid类型的变换。对非线性变换的参数进行估计，进一步增强了算法的非线性建模能力，提升了回声对消的效果。

1 SFLAF算法

1.1 函数连接型自适应滤波器FLAF

图1给出了一个函数连接型滤波器FLAF的结构。FLAF包括两个阶段：输入信号的非线性扩展以及后续的线性自适应滤波。假设在n时刻，FLAF接收到的输入信号向量为x(n)=[x(n)，x(n-1)，…，x(n-L+1)]，其中L表示输入向量的长度。FLAF利用函数扩展块(Functional Expansion Block，FEB)对其进行处理。FEB由一系列的函数组成，它们可以是正交基函数的完备集，满足Stone-Weierstrass近似定理[5]。FEB将输入信号进行扩展，映射到更高的维度，从而可以提高对系统的非线性建模能力。而所谓的函数连接(Functional Link)，本质上是就是FEB这个函数集合中的函数算子[6]。

图1 FLAF结构示意图

(1)

其中，0≤i≤L-1，L是输入向量原有的长度。

而对于长度为L的输入向量，经过FEB处理后，最终得到扩展向量hn。

=h0(n)，h(n)，…，hLe-1(n)〗T

(2)

其中，Le代表扩展后向量的长度，易得，Le=LQ。

FEB中函数集合的选择对FLAF的性能有重要的影响，需要根据具体的应用场景和处理的信号而定。这些满足Stone-Weierstrass近似定理的基函数，可以是正交多项式的子集，例如切比雪夫[7]、勒让德[10]和三角函数多项式[11]；也可以是近似函数，例如sigmoid函数和高斯函数。这其中，三角函数多项式由于在均方意义上能最好的表征任何的非线性函数，并且相较于幂级数多项式计算复杂度也较低，因此也被运用的最为广泛[8]。

考虑输入向量x(n)中的第i个元素，0≤i≤L-1，一般的三角函数FEB可以表示为：

(3)

其中1≤p≤P，P是三角函数连接扩展的阶数。而0≤j≤Q，在这种情况下，FEB中函数的个数Q=2P+1。1代表线性的元素，即没有通过三角函数变换，和输入向量中元素完全一样的元素。因此，这种情况下得到的扩展向量同时包含了线性和非线性的元素。

最后，只需要对扩展向量进行简单的线性滤波就可以完成整个FLAF过程。滤波器的目标就是在越小的误差范围内准确的对非线性建模。线性滤波器的权值向量记作w(n)=[w0(n)，w1(n)，…，wLe-1(n)]T，期望信号记作d(n)，则FLAF的误差信号表示为：

e(n)=d(n)-y(n)

=d(n)-hT(n)w(n)

(4)

可以看出，e(n)的最小化取决于对权值向量w(n)的估计。我们可以采用任意一种基于梯度下降法的自适应算法来更新权值向量[9]。

1.2 分裂函数连接型自适应滤波器SFLAF

分裂型FLAF(Split Functional Link Adaptive Filter，SFLAF)的结构如图2所示。所谓分裂，就是将经过FEB扩展后的信号中的线性元素和非线性元素解耦合，分别通过两个并行的自适应滤波器，用总体误差分别对两个滤波器的权值向量进行更新。这其中，线性滤波器接收未经过函数变换的输入向量，旨在估计回声路径；而非线性滤波器接收经过三角函数变换的向量，旨在对回声路径中的非线性变换建模[1]。

图2 SFLAF结构示意图

SFLAF的输出信号由线性滤波器和非线性滤波器的输出信号叠加而成：

y(n)=yL(n)+yFL(n)

(5)

2 SFLRLS-sigmoid算法

文献[2]提出了一种对回声路径中的非线性特性进行建模的有效方法：其将非线性畸变建模为sigmoid函数，并通过对其参数的估计来拟合非线性。其结构如图3所示。该算法分别用最小均方算法LMS和递归最小二乘算法RLS(Recursive Least Square，RLS)来更新sigmoid变换的参数和滤波器的权值向量。得益于RLS算法快速的收敛速度和跟踪能力，能快速使得估计值收敛到真实值。

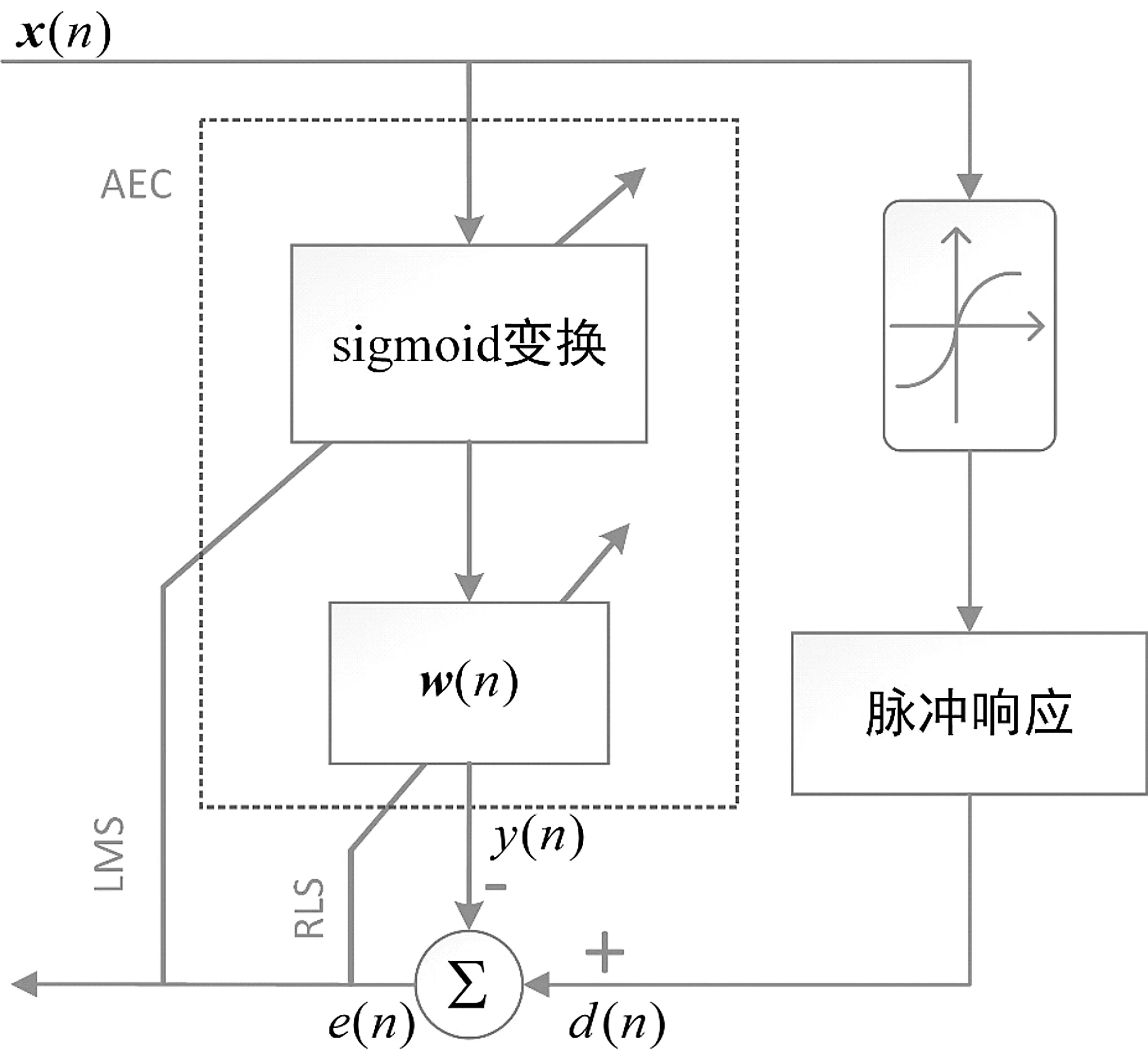
图3 RLS-sigmoid结构示意图

受此启发，我们将RLS-sigmoid算法引入到SFLAF的线性分支中，新的算法记作Split Functional Link RLS-sigmoid，SFLRLS-sigmoid。算法结构如图4所示。

图4 提出的SFLRLS-sigmoid算法结构示意图

首先对长度为L的输入信号x(n)分别进行sigmoid变换和函数扩展。输入信号x(n)通过(6)中的sigmoid变换：

(6)

其中，α和β是sigmoid变换的两个参数。得到xS(n)=[f(x(n)),f(x(n-1)),…,f(x(n-L+1))]。同时，输入信号x(n)通过三角函数连接进行函数连接扩展，得到扩展后的输入信号xFL(n)=[φ1(x(n)),φ2(x(n)),…,φ2P(x(n))]。

接着，分别将xS(n)和xFL(n)通过自适应滤波器：yS(n)=wST(n)xS(n)，yFL(n)=wFLT(n)xFL(n)；其中，wS(n)和wFL(n)为对应滤波器的权值。然后得到总体的滤波输出：y(n)=yS(n)+yFL(n)。将近端麦克风拾取到带回声的近端信号d(n)与总体滤波输出y(n)相减后再回送给远端，回送信号为总残差信号e(n)=d(n)-y(n)。

利用残差信号e(n)对下一次迭代的sigmoid变换的参数按照如下方法进行更新：

(7)

(8)

其中，α(n)和β(n)是在n时刻对α和β的估计值，μα和μβ是两个步长参数[2]。wS(n)利用递归最小二乘算法(RLS)更新：

P(0)=δ[-1]I

(9)

(10)

wS(n+1)=wS(n)+k(n)e(n)

(11)

P(n+1)=λ-1P(n)-λ-1k(n)xT(n)P(n)

(12)

其中，矩阵P(n)是逆相关矩阵，I是单位矩阵，k(n)是增益向量，λ和δ分别是遗忘因子和正则化参数[9]。wFL(n)利用归一化最小均方算法(NLMS)更新：

(13)

其中，μFL和σ分别是步长和正则化参数，‖·‖为二范数运算。

3 实验与分析

图5 回声路径的脉冲响应

按照以上实验条件，用本文方法与现有的两种方法进行回声消除实验，各种算法的参数具体取值如表1所示。图6给出了本文方法和文献[2]对sigmoid非线性变换的参数α和β的估计值的迭代曲线。可以看出，两种方法都能收敛到真实的参数值，而SFLRLS-sigmoid的收敛速度更快。

表1 实验各算法的最优参数近似取值

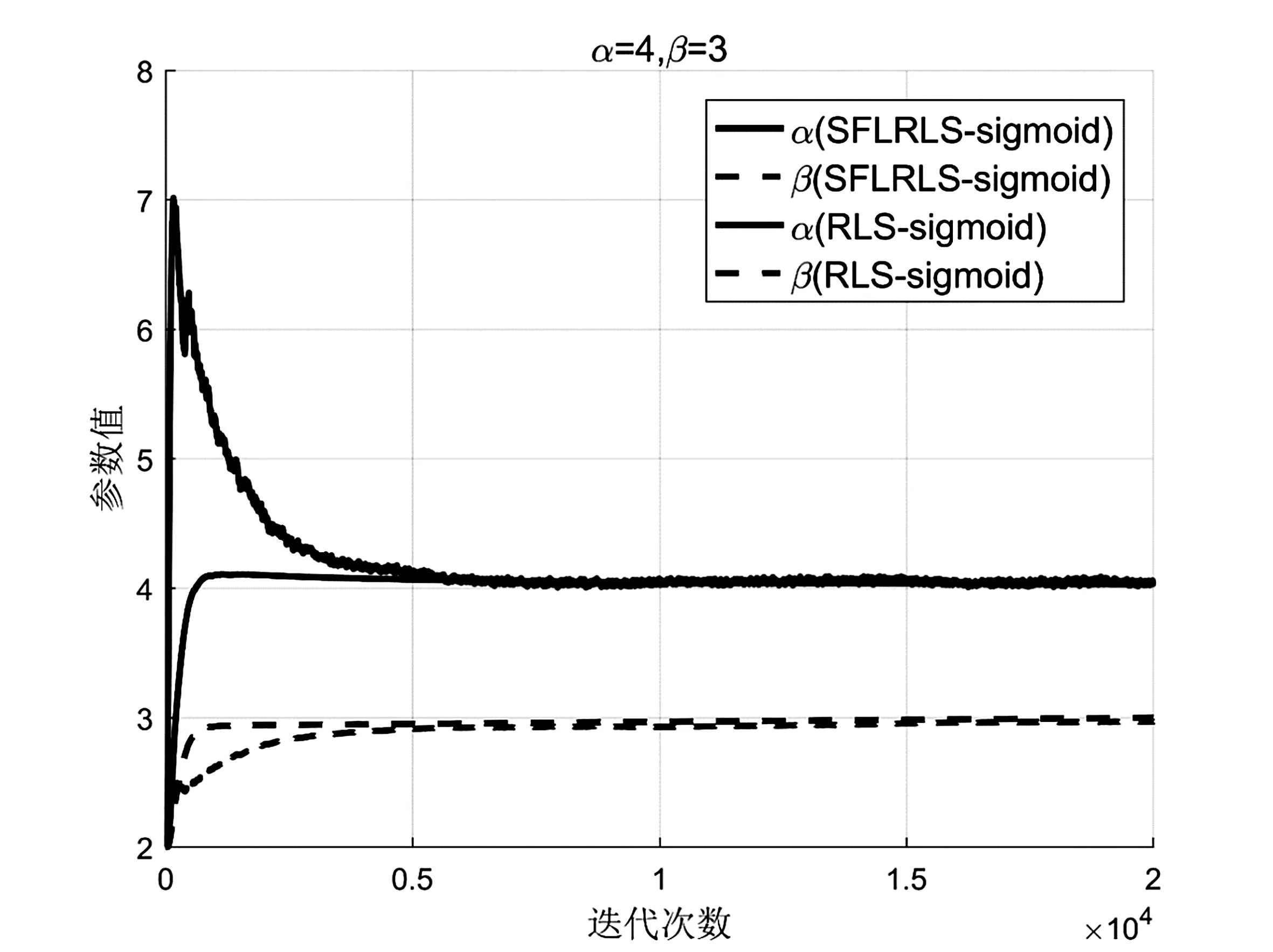
图6 sigmoid参数α和β学习曲线

选择回声返回损失增强(Echo Return Loss Enhancement，ERLE)作为性能指标：

其中，E{·}表示求期望运算。图7给出了3种方法的ERLE对比曲线。可以看出，由于RLS-sigmoid能准确估计sigmoid非线性变换的参数值，其效果要优于SFLAF。而本文方法在RLS-sigmoid的基础上与SFLAF结合，进一步加快了sigmoid非线性变换参数值的收敛过程。因此，相较于文献[1]、[2]的方法，本文方法的收敛速度更快，并且收敛稳定后的ERLE值也更大。