基于ARIMA模型的江苏省GDP的预测分析

肖东亚

【摘  要】GDP是衡量经济发展状况的一个重要指标，研究与预测GDP的发展趋势具有重要意义。论文运用EViews10和SPSS22软件，对1978-2020年江苏省GDP数据进行分析研究。在对数据进行进一步处理以及验证平稳性后，观察自相关图和偏自相关图，建立模型。之后根据AIC、SBC准则，从优选择ARIMA（0，1，1）模型。最后检验模型参数的显著性水平，发现系数显著非零。运用2016-2020年GDP的历史数据对模型拟合的好坏进行判断，得出平均相对误差较低、模型的拟合较好的结论。最后用ARIMA（0，1，1）模型对2021-2023年江苏省GDP数据进行了预测。

【Abstract】GDP is an important index to measure the economic development status. It is of great significance to study and predict the development trend of GDP. This paper uses EViews10 software and SPSS22 software to analyze and study the GDP data of Jiangsu Province from 1978 to 2020. After further processing the data and verifying the stationarity， the paper observes the autocorrelation graph and partial autocorrelation graph， and established the model. Then according to AIC criteria and SBC criteria， the paper selects the ARIMA （0，1，1） model preferentially. Finally， the significance level of model parameters was tested， and the coefficient was found to be significantly non-zero. Using the historical data of GDP from 2016 to 2020 to judge the quality of the model fitting， the conclusion is that the average relative error is low and the model fitting is good. Finally， the paper uses the ARIMA （0，1，1） model to predict the GDP data of Jiangsu Province from 2021 to 2023.

【关键词】ARIMA模型;GDP;预测

【Keywords】ARIMA model; GDP; prediction

【中图分类号】F224;F127                                             【文献标志码】A                                                 【文章编號】1673-1069（2021）07-0120-02

1 引言

GDP是衡量一个国家或者地区经济发展状况的重要指标，它反映了该国家或者地区的经济实力和市场规模。所以，对未来GDP作出准确的预测能为宏观经济健康发展起导向性作用，有利于决策机构作出更好的决策[1]。但是，近几年受国家产业调整等多种因素影响，导致GDP增速放缓。这无疑增加了GDP预测的难度。本文选取了1978-2020年江苏省的GDP数据，建立了ARIMA模型，并用2016-2020的历史数据对模型进行了检验，发现误差较小，于是运用模型对2021-2023年的GDP作出了预测。

2 ARIMA模型基本原理

ARIMA模型又称为求和自回归移动平均模型，由博克思和詹金斯最先提出。该模型的基本思想是：将预测变量随时间变化而形成的序列作为随机序列，其后以时间序列的自相关性为基础，用特定的数学模型来描述该随机序列[2]。

3 实证分析

3.1 数据来源

本文选取的数据是1978-2020年期间江苏省的GDP数据。为确保数据的准确性与真实性，1978-2019年GDP数据来自《江苏统计年鉴2020》，2020年GDP数据来自江苏省统计局官方发布的文件。

3.2 数据的平稳性分析及处理

1978-2020年江苏省GDP数据有明显趋势，为非平稳数据，需要进一步处理。先对数据进行对数处理，发现数据依旧明显是非平稳的。之后再对数据进行一次差分，得到的数据没有了明显趋势，可以进行时间序列分析。

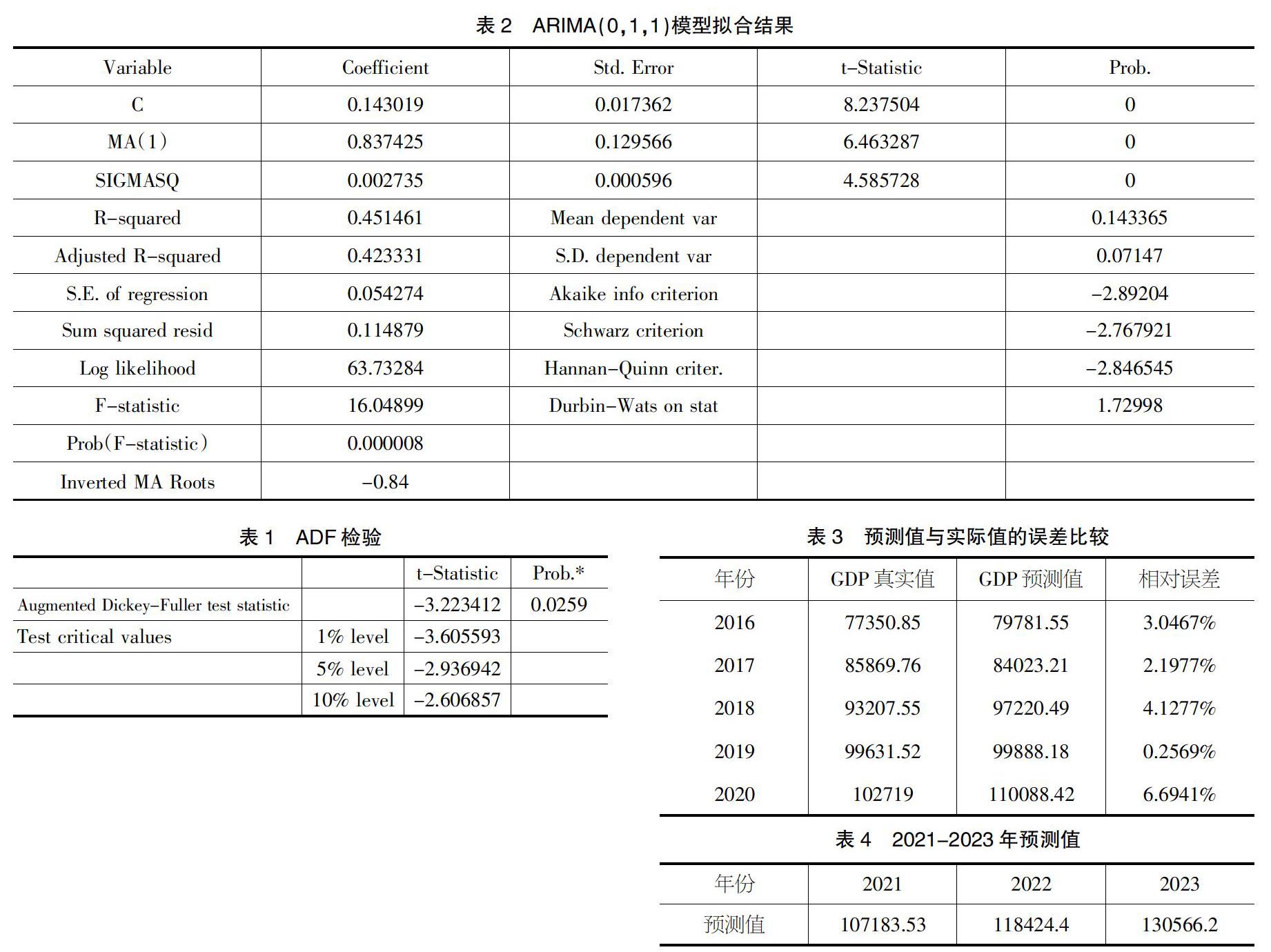
对处理过的数据进行ADF检验，如表1所示，P为0.0259，小于0.05，说明该数据为平稳数据。

3.3 ARIMA模型的建立与模型参数的显著性检验

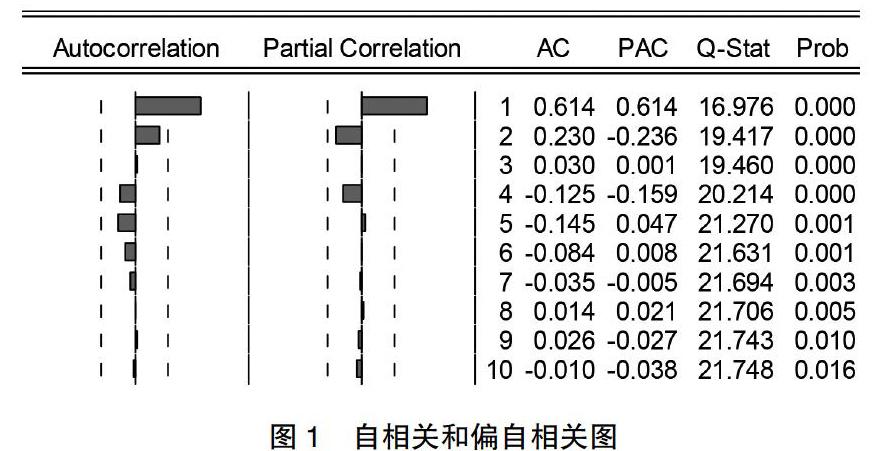
处理过后的GDP数据的自相关图如图1所示，数据的自相关系数为零阶拖尾（自相关系数的第零階为方差），偏自相关系数呈现一阶截尾。所以尝试非中心化的ARIMA（0，1，1）模型和ARIMA（0，1，2）等模型。尝试之下发现只有ARIMA（0，1，1）模型和ARIMA（0，1，（2））模型的解释变量的参数估计值在5%的显著性水平下是显著的。但是ARIMA（0，1，1）模型的AIC和SBC比ARIMA（0，1，（2））模型的小，所以从优选择ARIMA（0，1，1）模型。模型的拟合结果如表2所示。从表中可以看出常数C和MA（1）的系数显著非零。

3.4 ARIMA模型的分析与预测

为进一步检验模型拟合的好坏，本文选取了2016-2020年共5年的GDP数据，计算GDP真实值与预测值的相对误差，如表3所示。除2020年因为疫情的原因导致预测的误差过大，其他的年份GDP的相对误差都在5%以内，平均相对误差为3.2646%，模型的误差较小，预测的准确度高。之后根据ARIMA（0，1，1）模型预测2021-2023年的GDP，结果如表4所示。

4 结语

本文运用1978-2020年江苏省GDP的数据，通过模型参数的显著性检验，再根据AIC和SBC准则从优选择ARIMA（0，1，1）模型，并用2016-2020年的历史数据去检验模型拟合的好坏。除2020年因为疫情的原因，预测的数据误差较大之外，其他年份GDP的相对误差都在5%以内，平均相对误差为3.2646%，模型的拟合较好，准确度较高，能较为准确地预测数据，可以为决策机构提供一定的参考。从预测的结果来看，2021-2023年江苏省GDP仍会保持稳定增长，这符合国家平稳转型的战略。但由于ARIMA模型本身的特性，只能预测GDP的数值，对外界经济环境作出重大改变时无法作出一定的调整，这就导致模型预测的误差较大，所以模型本身是有待进一步改进的。

【参考文献】

【1】王鄂，张霆.时间序列在湖南省GDP预测中的应用——基于ARIMA模型[J].青岛大学学报（自然科学版），2019，32（3）：136-140.

【2】蒯梦娟.基于ARIMA模型及回归分析的安徽省GDP预测研究[D].合肥：安徽农业大学，2015.

【3】易丹辉，王燕.应用时间序列分析（第5版）[M].北京：中国人民大学出版社，2019.