《空间中垂直关系的证明——面面垂直》教学设计

邓 丽

(云南省昆明市西南联大研究院附属学校 650000)

课型：一轮复习课.

一、教学内容分析

1.考点分析

立体几何中有关“线线、线面、面面”位置关系(平行与垂直)的证明是历届高考命题的热点.而“线线、线面、面面”三个垂直关系在高考命题设计中多以面面垂直来呈现，主要以棱柱、棱锥为载体，经常把三个垂直关系的判定和性质作为考查的重点.本考点对学生基本能力要求如下：

(1)能以相关的定义、公理和定理为出发点，认识和理解空间中线面垂直、面面垂直的判定与性质定理.

(2)会运用线面垂直、面面垂直的判定及性质定理证明一些简单空间图形的垂直关系问题.

(3)灵活处理好“线线、线面、面面” 三种垂直关系的相互转化，为后续计算相关的角度问题与距离问题奠定逻辑推理基础，积累逻辑推理经验.

2.重点与难点

线面垂直.

3.思想与方法

涉及到数形结合、转换与化归、特殊到一般等数学思想和类比、归纳、转换与化归等数学方法.

4.学科核心素养

问题编排上渗透了直观想象、数学抽象、数学建模、逻辑推理等数学核心素养.

5.预设教学效果

为让学生初步达成“脑中有形——直观想象；心中有数——数学抽象；手中有术——数学建模、数据分析；解题有路——逻辑推理、数学运算”之效果奠定基础.

二、学情分析

在高一、二期间学生系统的学习了立体几何，初步认识和了解空间中线面垂直、面面垂直的有关判定与性质定理，对三种垂直关系有了一定的知识储备.

多数学生的立体几何基础较弱，特别是文科学生,其空间想象能力还存在一定的困难，对知识的领悟与定理的运用与理科学生存在一定的差距.证明空间中面面垂直的方法有定义法和判定定理法.本节课教学主题定位在利用面面垂直的判定定理来证明面面垂直.所以，首先要有意识地让学生通过简单的正方体模型来观察并证明面面垂直，然后归纳提炼出面面垂直的判定定理.

如何在具体的模型中快速找到其中一个平面内的直线与另一平面垂直，进而将线面垂直转化为面面垂直，给足学生思考的时间和空间，充分化解学生的认知冲突，化难为易，化繁为简，突破难点.

三、教学流程

四、教学设计

设计意图：以问题为主导——忆模，以学生为主体——研模，以探究为主线——拓模，以发展为主题——升华.

今年是我们伟大祖国70岁的生日，看70周年阅兵的时我们感慨祖国的繁荣昌盛.作为一名中国人我感到无比自豪，当然祖国的复兴离不开每一代人的努力奋斗(千千万万的你我他).阅兵方阵的每一行每一列的军人所构成的平面与长安街的底面都是垂直的.可见生活中的面面垂直是无处不在的.下面我们走进数学中的面面垂直.

板块一：忆模

图1

图2

问题1 已知正方体ABCD-A1B1C1D1，求证：平面ACC1A1⊥平面D1DBB1.

证明1∵平面AC为正方形，∴AC⊥BD

又∵AA1⊥平面ABCD，∴AA1⊥BD

∴BD⊥平面AA1C1C，且BD平面BB1D1D

∴平面AA1C1C⊥平面BB1D1D

证明2∵平面AC为正方形，∴AC⊥BD

又∵BB1⊥平面ABCD，∴AC⊥BB1

∴AC⊥平面BB1D1D，且AC平面AA1C1C

∴平面AA1C1C⊥平面BB1D1D

问题2 你能总结如何证明面面垂直？

面面垂直的判定定理：(线面垂直⟹面面垂直)如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.

设计说明：让学生从熟悉的正方体模型中回忆面面垂直模型，并从具体的模型中抽象出面面垂直的判定定理.

问题3在正方体ABCD-A1B1C1D1中，是否还存在过直线BD的截面与平面AA1C1C垂直？

存在.例如：平面A1BD或平面C1BD.

板块二：研模

问题4已知正方体ABCD-A1B1C1D1，求证：平面ACC1A1⊥平面A1BD.

图3 图4

证明∵平面AC为正方形，∴AC⊥BD

又∵AA1⊥平面ABCD，∴AA1⊥BD

∴BD⊥平面AA1C1C，且BD平面BB1D1D

∴平面AA1C1C⊥平面BB1D1D

问题5问题1与问题4的证明过程有什么区别与联系？(变与不变)总结证明面面垂直的关键问题是什么？

变：BD在不同的平面.问题1两个平面都容易找到一条直线与另一平面垂直.问题4只能在一个平面找.

不变：都可以通过证明BD垂直平面AA1C1C证明面面垂直.

关键问题：线面垂直.

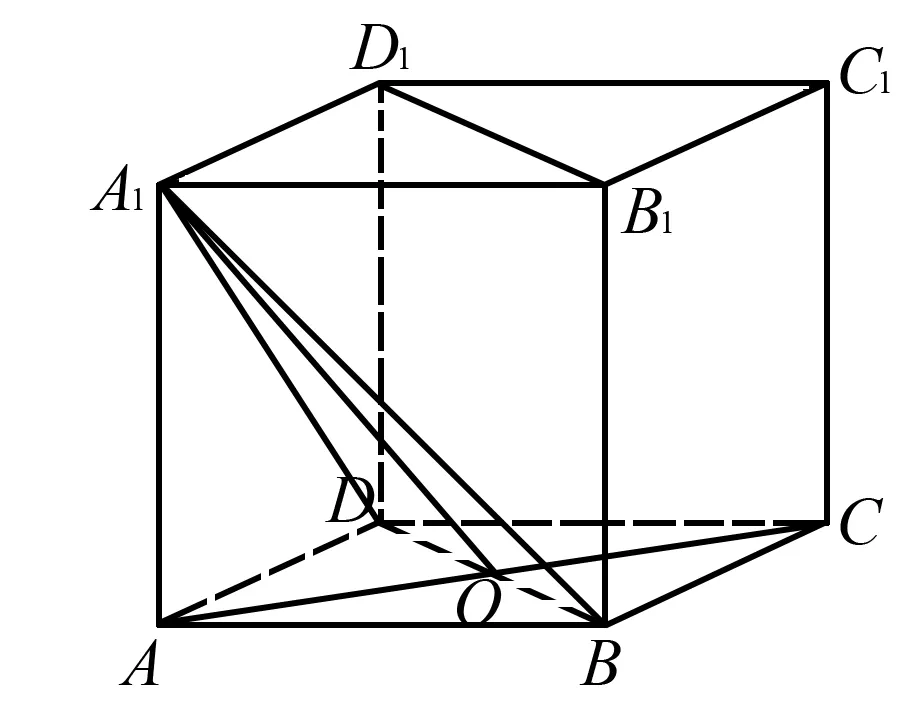
图5

问题6还有没有其它的证明方法？

证明：记直线AC与BD的交点为点O.连接A1O

∵平面ABCD为正方形，∴AO⊥BD

又∵A1D=A1B，∴BD⊥A1O，且A1O∩AO=O

∴BD⊥平面AA1C1C，且BD平面BB1D1D

∴平面AA1C1C⊥平面BB1D1D.

问题7证明面面垂直是如何转化的？最后落实在哪里？如何实施？

面面垂直⟹线面垂直⟹线线垂直(空间⟹平面⟹平面)

问题8如果挪动AA1的位置使得AA1不垂直面ABD，其他条件不变，平面A1OA与平面A1BD是否仍然垂直？

图6 图7 图8

成立.其中的垂直关系并没有变.

设计说明研究面面垂直模型，以及面面垂直模型的关键问题和本质.(线面垂直和线线垂直)以及如何在面面垂直模型中找准(线面垂直).

板块三：拓模与升华

问题9：如图1，要使平面PAD⊥平面ABCD，需要添加什么条件？

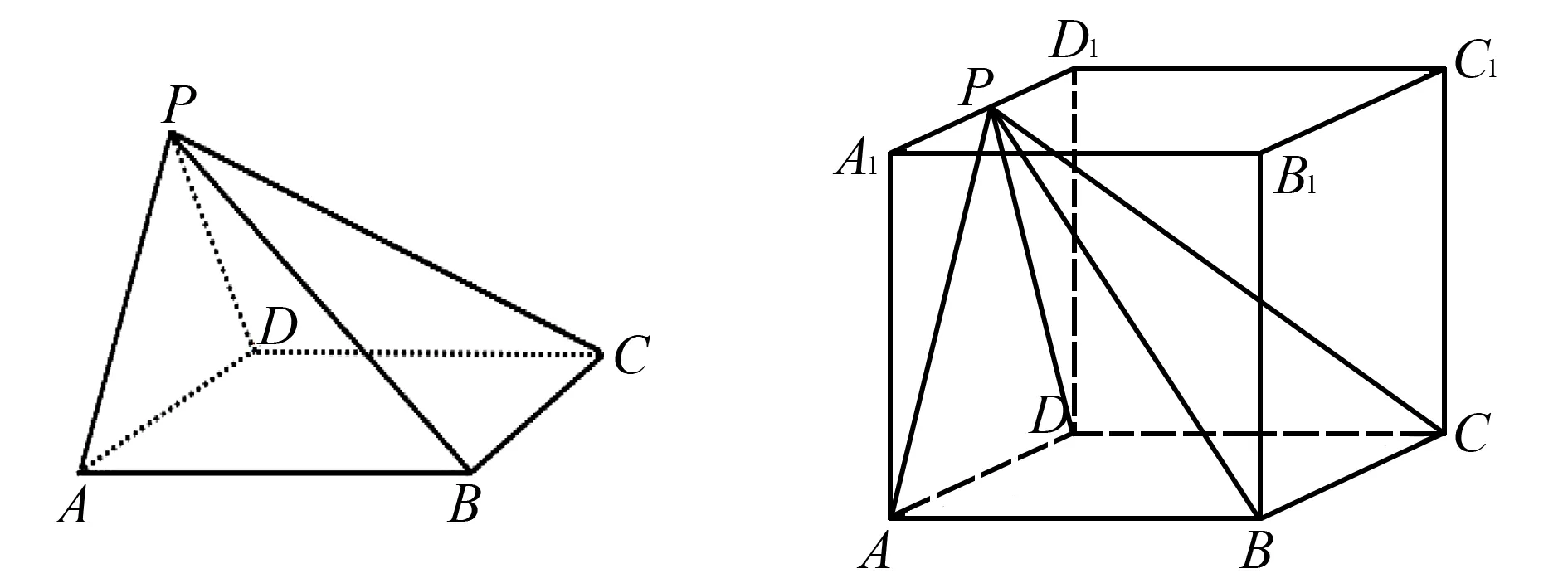
图9 图10

必要时可以提醒学生四边形ABCD为矩形、菱形.或者对三角形PAD为等腰三角形.

例如：已知四边形为矩形ABCD，PA⊥AB,求证：平面PAD⊥平面ABCD.

设计说明拓展面面垂直模型，让学生依托正(长)方体模型对面面垂直模型进一步探究，克服文科生对空间垂直的畏难情绪.让学生对各种锥体和柱体能在熟悉的正(长)方体模型中寻找原型.遇到面面垂直模型大胆猜想，小心证明.

挑战：同学们能否自己借助正方体构造一个面面垂直模型并设计好条件.(或者学习过的面面垂直模型在正(长)方体中找到原型)

五、学生小结(并画出思维导图)

利用面面垂直的判定定理证明面面垂直

面面垂直⟹线面垂直⟹线线垂直(空间⟹平面⟹空间)

六、体会与感悟

本节课是高三一轮复习复习课，整个教学设计是基于问题和基于学情进行开展，尽可能让复习走向关联与交汇，并通过追问与反思让学生自主完成教学内容.其中第三环节(拓模)是难点.

通过让学生自主证明他们所熟悉的正方体中的对角面互相垂直出发，让学生回忆用面面垂直的判定定理来证明面面垂直，培养学生的逻辑推理与数学建模的意识.在环节二中，引导学生对面面垂直模型的关键问题和本质进行归纳，让学生通过类比方式进行学习，并能归纳梳理空间中线线垂直的基本类型.在环节三给出结论让学生寻找条件，培养学生的分析问题的能力和逆向思维能力.

著名的数学家波利亚说过：“学习任何东西最好的途径是自己去发现”，也正本节课的设计理念，利用“最近发展区”原理，创设问题情境让学生在自主、合作、探究中去完成学习任务，当学生可能会遇到困难时，教师再予以适当的引导与点拨.