聚乙烯拉伸屈服应力-分子结构预测模型研究
2021-08-06王金刚高凌雁
王金刚,高凌雁,郭 锐,栾 凌
(中国石油化工股份有限公司齐鲁分公司研究院,山东 淄博 255400)
聚乙烯具有优良的化学稳定性、力学性能和电绝缘特性,广泛应用于薄膜、包装材料、电线电缆、管道、汽车、建筑等领域。拉伸屈服应力是制约聚乙烯应用的一项关键性能,同时也是聚乙烯性能测试和质量控制的重要指标。聚乙烯的整个拉伸过程可分为弹性形变和不可逆形变两个阶段。拉伸初始阶段应力变化较大,但此阶段球晶的变形是弹性的,在撤去外力后依然可以恢复原状,因此材料在此阶段发生的是弹性形变。随着形变的继续增大,当达到一定值时会出现应力变化较小而应变却急剧增长的现象,即屈服现象,使材料发生屈服时的应力就是材料的屈服应力[1]。试样屈服时,球晶中剪切形变占主导,这时组成球晶的层晶之间的连接发生破坏,进而产生滑移和解体,这些都是不可逆的变动。因此,屈服是由可逆形变到不可逆形变的转折点,也是材料能否继续使用的临界点,对材料使用性能至关重要。
拉伸性能测试需要原料较多,小试聚合获得原料难以满足,而结构测试一般需要原料较少,建立聚乙烯拉伸屈服应力与结构参数的关联模型既有利于促进催化剂和聚合工艺的研究,同时对定制开发聚乙烯新产品,指导现有产品性能提升、加工应用及质量控制等具有重要意义。目前,国内外聚乙烯模型研究大多适用范围较窄且侧重于生产过程中熔体流动速率、密度两个主要参数的计算,对力学性能、加工性能等决定产品用途的性能研究较少[2-4]。本工作对国内外17种采用不同装置和催化剂生产的聚乙烯进行分析,通过拟合法建立了聚乙烯拉伸屈服应力与分子结构的关联模型,并进行了验证。
1 实验部分
1.1 主要原料
主要原料见表1。

表1 主要原料Tab.1 Main raw materials
1.2 主要仪器与设备
Z00P型程控压机,德国Collin公司;4467型万能试验机,美国Instron公司;PL-GPC220型凝胶渗透色谱仪,英国Polymer Laboratories公司;is50型红外光谱仪,美国Thermo Scientific公司。
1.3 测试与表征
拉伸试样状态调节按GB/T 2918—2018进行。拉伸性能按GB/T 1040.1—2018测试。相对分子质量及其分布采用凝胶渗透色谱(GPC)法,色谱柱为2根串联,溶剂及流动相均为1,2,4-三氯苯(含质量分数为0.1%的抗氧剂2,6-二丁基对甲酚),柱温150 ℃,溶解4 h,流量1.0 mL/min,采用窄分布聚苯乙烯为标样。支化点含量采用核磁共振波谱法按SH/T 1816—2017测试。
2 模型的建立
聚乙烯拉伸屈服应力的主要影响因素包括相对分子质量及其分布、支化点含量、共聚单体种类和热历史[5]。其中,共聚单体种类和热历史很难量化,因此,对所有聚乙烯试样结构与性能的测试均采用相同条件和程序,以消除热历史对其影响。本工作只建立了乙烯-1-丁烯共聚物的拉伸性能模型,可不考虑共聚单体种类的因素。建立模型所用数据见表2。

表2 建立模型所用数据Tab.2 Data for model establishment
从图1可以看出:拉伸屈服应力与支化点含量的关系规律性较好,随支化点含量的增加而减小;与重均分子量和相对分子质量分布的变化规律性不明显,因此判定支化点含量为拉伸屈服应力最主要的影响因素。

图1 拉伸屈服应力随重均分子量、相对分子质量分布、支化点含量的变化曲线Fig.1 Tensile yield stress as a function of weight-average molecular weight,relative molecular mass distribution,and content of branch point
通过数据分析,模型的建立应具有一个因变量,三个自变量,因此,应用Origin软件,采用线性拟合与多元非线性拟合相结合的逐步拟合法建立了拉伸屈服应力与支化点含量、重均分子量和相对分子质量分布的关系模型。
一次拟合:由于拉伸屈服应力随支化点含量的变化呈线性递减规律,因此,采用线性拟合法建立拉伸屈服应力与支化点含量关系的初步模型。从图2可以看出:拟合直线与原始数据相关度约为0.97,一次拟合所得关系式为:Y′=A′-B′X1(其中,X1为支化点含量,下同;模型系数A′=25.971 16,B′=0.791 63)。

图2 拉伸屈服应力与支化点含量的线性拟合结果Fig.2 Linear fitting results of tensile yield stress-branch point
从表3可以看出:一次拟合后,PE4,PE10,PE16,PE17的位伸屈服应力实测值与计算值偏差较大,相对误差均大于2.00 MPa。其他试样的相对误差为0.11~1.77 MPa。

表3 一次拟合后拉伸屈服应力相对误差较大的4种树脂Tab.3 Four resins with large relative error after first fitting
二次拟合:采用多元非线性拟合法,在一次拟合的基础上增加重均分子量的影响,建立二次拟合模型:Y=A+B(A′-B′X1)-ClgX2(其中,X2为重均分子量,下同;模型系数A=17.278 93,B=1.052 85,C=3.578 1,A′=25.971 16,B′=0.791 63)。从表4可以看出:加入重均分子量作为自变量进行二次拟合后,4种树脂拉伸屈服应力的相对误差均大幅减小。

表4 二次拟合后4种树脂拉伸屈服应力的相对误差Tab.4 Relative errors of four resins after secondary fitting
三次拟合:仍然采用多元非线性拟合法,在一次拟合的基础上同时增加重均分子量、相对分子质量分布两个自变量,建立三次拟合模型:Y=A+B(A′-B′X1)-ClgX2+DX3(其中,X3为相对分子质量分布;模型参数A=32.152 78,B=1.005 34,A′=25.971 16,B′=-0.791 63,C=6.497 71,D=0.099 39)。从表5可以看出:经过三次拟合,4种树脂拉伸屈服应力的相对误差进一步缩小,因此,将三次拟合模型作为最终建立的拉伸屈服应力-分子结构预测模型。

表5 三次拟合后4种树脂拉伸屈服应力的相对误差Tab.5 Relative errors of four resins after third fitting
3 模型验证
3.1 准确性验证
相对误差可以反映模型可信程度。本工作采用平均误差来验证模型的准确性。将参数带入模型计算平均误差,从表6可以看出:拉伸屈服应力平均误差为0.97 MPa,说明计算值与实测值相差不大,证明建立的拉伸屈服应力-分子结构预测模型准确性良好。
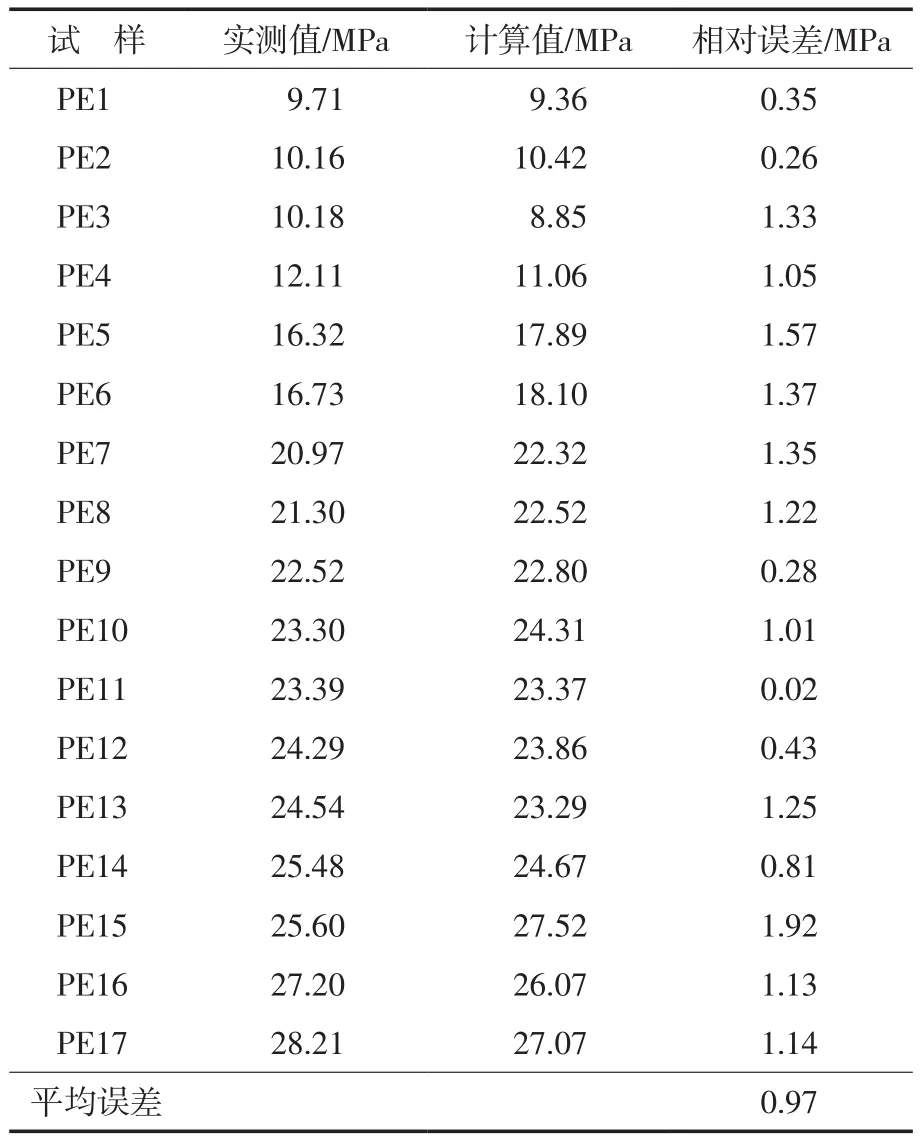
表6 准确性验证Tab.6 Accuracy verification
3.2 应用验证
选取2种未参与建模的聚乙烯带入模型进行验证,从表7可以看出:将采用进口钛系催化剂生产的LLDPE(即PE18)和采用国产铬系催化剂生产的HDPE(即PE19)的相关参数带入模型进行验证。PE18,PE19拉伸屈服应力的相对误差分别为0.03,0.12 MPa,说明模型准确性良好,可以用于指导聚乙烯催化剂及新产品开发和加工应用。
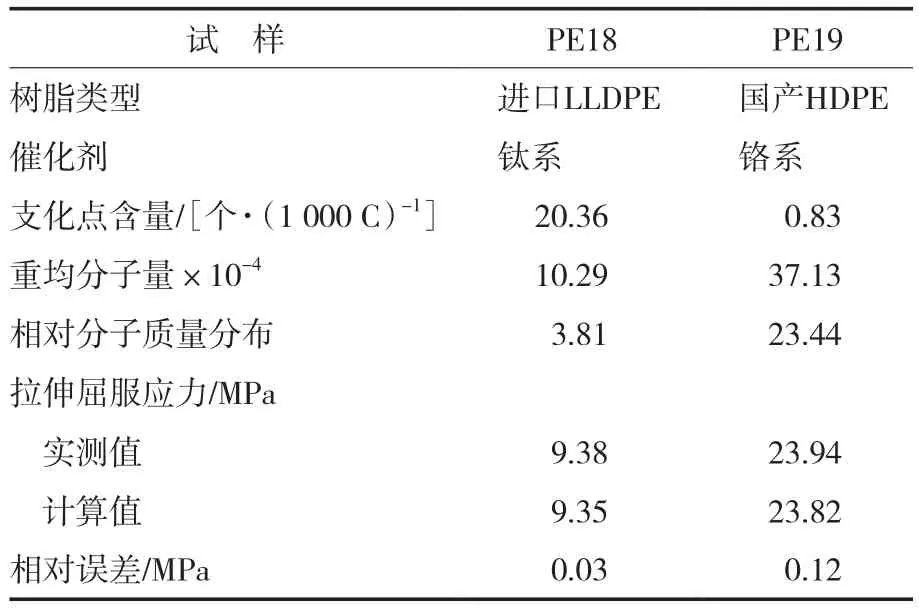
表7 模型应用验证Tab.7 Model validation in application
4 结论
a)通过分析聚乙烯拉伸性能的主要影响因素,以支化点含量、重均分子量和相对分子质量分布为自变量,拉伸屈服应力为因变量,实验数据为基础,采用线性拟合与多元非线性拟合相结合的方法建立了拉伸屈服应力-分子结构预测模型。
b)通过准确性验证及应用验证表明,该模型准确性良好,可以用于指导聚乙烯催化剂及新产品开发和加工应用。
