卷积神经网络和支持向量机算法在塑料近红外光谱分类中的模型应用

张文杰，焦安然，田 静，王晓娟，王 斌，徐晓轩

（1．南开大学 物理科学学院 弱光非线性光子学教育部重点实验室，天津 300071；2．江苏大学 食品与生物工程学院，江苏 镇江 212013；3．宁波海关技术中心，浙江 宁波 315048）

塑料自发明以来为人类生产生活提供了便利，得到了应用广泛。但由于大多塑料制品化学性质稳定、不可降解，导致产生了大量塑料废弃物。2018年环境规划署发布的数据表明全世界塑料废弃物年产量约3亿吨。我国是世界上十大塑料制品生产和消费国之一，塑料废弃物的分类回收再利用十分重要，否则不仅会污染环境，还会造成资源浪费。根据欧洲塑料加工协会的一项调查结果，超过76%的欧洲塑料加工商认为改善塑料废弃物的收集和分类是提高再生塑料质量的最佳方式［1］。传统的塑料分类方式如人工分类法、光学分选法、浮选法［2－5］等耗时耗力，为节约劳动力成本，并精确、高效地进行塑料分类，人们研究了塑料的智能分类算法。如，激光诱导击穿光谱（LIBS）技术和主成分分析（PCA）已成功用于鉴定聚对苯二甲酸乙二醇酯（PET）、高密度聚乙烯（PE）、聚丙烯（PP）和聚苯乙烯（PS）［6］。LIBS技术也可以识别具有相同聚合物基体但添加剂不同的塑料/聚合物样品［7］。X射线吸收光谱（XAS）结合PCA和反向传播神经网络（BPNN）被用于识别15种不同塑料［8］。拉曼光谱和K近邻算法（KNN）、循环子空间回归（CSR）、库搜索被用于塑料分类［9］。衰减全反射傅里叶变换红外光谱结合主成分分析及系统聚类分析（HCA）被用于对7类废旧塑料进行分类鉴别，通过选择余弦和平均距离法作为样品间以及类间距离函数对数据进行聚类，最终得到100%的分类准确率［10］。而分类和回归模型（CART）可以从近红外光谱数据中找到直接和简单的分类条件［11］。研究者们正不断探索系统使用近红外光谱分析技术进行塑料分类的方法。

近红外光谱主要由含氢基团振动的合频、倍频组成［12］，包含吸收峰的强度和位置差异等丰富信息，因快速、无损的特点得到了广泛应用。由于大多数塑料聚合物分子在近红外光谱区域可以提供特征信息［13］，因此近红外光谱分析技术结合传统的机器学习算法如KNN、PCA、CART等可用于塑料的检测。塑料分类还可使用支持向量机（Support vector machines，SVM）和深度学习的分类算法。SVM是典型的有监督分类算法之一，在1993年由Corinna Cortes和Vapnik提出［14］，可以根据给定类别的数据点确定一个超平面，将新的数据点划分在不同类别。而卷积神经网络（Convolutional neural networks，CNN）作为深度学习的热门之一，在图像分类等方面有出色的性能。全连接的人工神经网络方法需要训练的参数太多，时间成本大。而CNN的神经元只感知局部信息，同一层中使用的卷积核参数共享，使得需要训练的参数数量大大减少。近红外光谱数据在空间上有关联形成特征，且每个空间上采样原理一致，适合用CNN学习［15－18］。

PP（聚丙烯）和PE（聚乙烯）是常用的塑料材料，可用于生产生活中的薄膜类制品、注塑制品、管材类制品、丝类制品等。通常塑料废弃物中PP塑料和PE塑料的比例在70∶30（汽车废料）～25∶75（包装废料）之间变化，不适合直接生产高质量的产品（高质量产品的生产应满足两种塑料的纯度达到97%［19］）。PP、PE塑料都包含―CH2和―CH3官能团，有相似的化学结构，因而高效区分PP和PE塑料对其回收再利用有重要价值［20］。本文基于100组4种塑料样本（PP新生料、PP再生料、PE新生料、PE再生料）的近红外光谱数据，建立了一维卷积神经网络（1D CNN）模型，将其用于小数据集的预测，并与支持向量机模型进行比较，开发了快速准确的塑料分类方法。

1 实验部分

1.1 样品与光谱采集

塑料样品由宁波市检验检疫局提供，包括PP和PE两种塑料共100个。其中PE再生料（PE recycled material，简写为PEr）32个，PE新生料（PE new raw material，简写为PEn）36个，PP再生料（PP recycled material，简写为PPr）15个，PP新生料（PP new raw material，简写为PPn）17个，类别分别标记为0、1、2、3。

塑料的近红外光谱数据由江苏大学食品与生物工程学院提供，使用棱光技术S450近红外光谱分析仪采集。设置波长范围为900～2 500 nm，在室温（25℃）下将装有塑料样品的样品杯置于采集窗口进行光谱采集，每个塑料样品扫描3次，取其平均光谱数据。

采集的100个样品的光谱图如图1A所示。根据光谱图比对数据，剔除掉PP再生料中2个异常样本的数据，得到的光谱图如图1B。

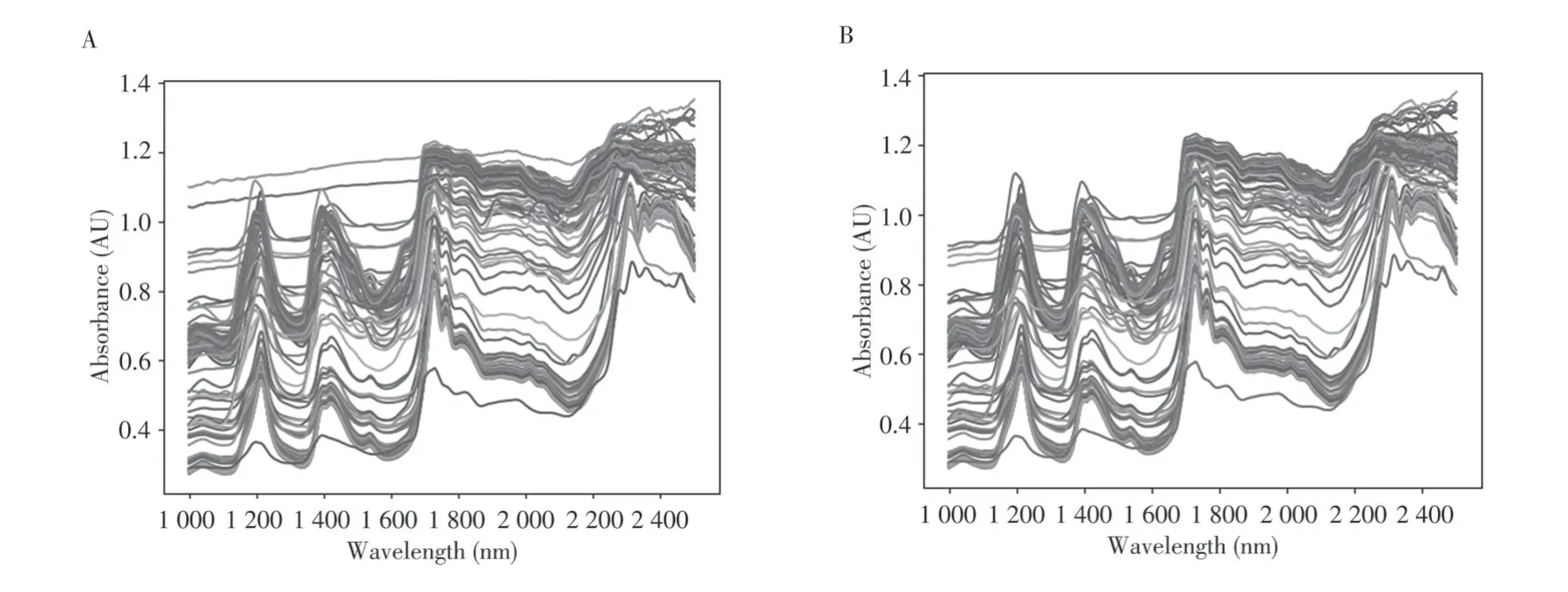
图1 塑料样品的原始光谱图（A）与剔除异常值后的光谱图（B）Fig．1 Raw spectra of plastic samples（A）and spectra after data cleaning（B）

4类塑料样品均采用随机选择法（RS），按照训练集与验证集近似3∶1的比例进行样品集划分。最终将98个有效样本分为训练集样品72个，验证集样品26个。具体信息如表1所示。

表1 塑料样品信息统计表Table 1 Statistical table of 98 plastic samples

1.2 数据预处理

为了减少光谱中背景噪声以及样品散射对模型的影响，在建模之前，分别采用一阶导数法（The first derivative，1st Der）、二阶导数法（The second derivative，2nd Der）、中心化（Centralization）、标准化（Standardization）、Savitzky－Golay平滑法（Savitzky－Golay smoothing method，SG）、多元散射处理（Multiplicative scatter correction，MSC）、标准正态变换法（Standard normal variate，SNV）对光谱数据进行预处理。在建立支持向量机模型之后，根据实验结果，选择最合适的数据预处理方法。

1.3 支持向量机模型

支持向量机一般被用来解决二分类问题，现在也可以处理多分类问题。可以使用一对多（Oneversus－all，OVA）或一对一（One－versus－one，OVO）方式将多分类问题转化为二分类问题［21］。其基本原理是寻找一个超平面ωTx+b=0，使训练集中不同类别的点落在超平面的两侧，同时使超平面两侧的空白区域达到最大［22］。使用不同的核函数可以将样本映射到高维空间找到超平面，因而支持向量机可进行线性分类和非线性分类。

对于线性可分的数据集，目标函数为：

服从约束条件：

对于公式（1）～（4），n为样本数量，ω和b分别是超平面ωT x+b=0的权重和偏置参数，x i和y i表示第i个输入的向量和第i个因变量值。使用拉格朗日乘子法可以求解上述极值。

支持向量机近年来被引入化学计量学领域，并且成功应用于中红外和近红外光谱分类任务［23］。建模后，进行4折交叉验证，通过比较不同数据预处理方法的准确率，选择准确率最高的模型。选择使模型效果最好的参数：使用OVO方法，即在每两个类之间都构造一个二分类SVM模型；惩罚因子C的值设为256，核函数为线性核函数。输入塑料的近红外光谱数据和相应的类别标签（0、1、2、3），按照表1的比例随机选取10个验证集进行10次实验。模型输出包括预测得到的标签、训练集准确率和验证集准确率。

1.4 一维卷积神经网络模型

卷积神经网络作为一种非线性模型，可以有效提取光谱中的局部信息，学习能力强。

典型的卷积神经网络模型包含输入层、卷积层、池化层、全连接层、输出层。对于光谱数据，输入层输入一维光谱数据比二维光谱矩阵更加高效［17］。输入数据和标签后，卷积层使用多个设定好大小和步长的一维卷积核经卷积运算后得到特征图。池化层通常在卷积层之后用来提取数据的局部特征。经过一个或者多个全连接层，可将特征映射到样本空间进行分类。激活函数使用ReLU函数可以避免梯度消失问题；而在分类问题中，神经网络的最后一层通常使用Softmax函数，将输入映射为0到1之间，作为对应类别的概率。模型训练时，首先初始化权值，输入塑料样本训练集近红外光谱数据及类别标签，经过神经网络各层得到最终输出结果。计算模型损失函数值，通过反向传播将损失函数值从最末层传至网络各层，按照最小化损失函数值的方向更新权值，继续训练。

本实验构建了一个6层一维CNN（1D CNN）用于塑料分类，包括输入层－卷积层C1－池化层S2－全连接层F3－全连接层F4－输出层，如图2。将训练集表示塑料类别的标签值“0、1、2、3”转化为one－hot向量输入，每个样本光谱数据输入维度为1 501×1。为了尽可能避免过拟合现象，在神经网络中添加了正则项和随机失活（Dropout）。为降低模型复杂性，仅使用一层卷积层，8个卷积核，大小为3×1，步长为1。池化层使用最大池化法，核的大小为2×1，步长为2。模型最后一层全连接层使用Softmax激活函数，优化器为AdamOptimizer，学习率为0．000 1，卷积核个数为3，全连接层神经元个数为60，迭代次数为5 000。模型训练基于TensorFlow框架GPU版本。

图2 一维CNN模型各层结构示意图Fig．2 Representation of one-dimensional convolutional neural network（1D CNN）architecture

使用与MSC－SVM模型相同的10组验证集进行实验，得到预测类别和预测准确率。

1.5 评价指标

将训练集和测试集的分类准确率作为模型评价指标。准确率P为分类正确的样本数Nc占总样本数Nr的比例，由式（5）得到：

2 结果与讨论

在建立SVM模型时，比较了不进行数据预处理以及不同数据预处理方法建模后的交叉验证实验结果，如表2所示。

表2 不同数据预处理的SVM模型准确率Table 2 Comparison of validation accuracy using different SVM models

可见采用MSC后模型准确率最高。选择分类性能最好的MSC－SVM模型进行10次随机实验，98个样本共得到结果980次，其中训练集720次，验证集260次。将这980次结果进行统计，记录不同塑料种类的分类结果，将其真实值和预测值在表格中体现，得到混淆矩阵，如表3所示。类似的，记录1D CNN模型10次随机实验共980次分类结果的混淆矩阵，如表4所示（每次随机实验验证集与MSC－SVM模型使用的对应验证集相同）。混淆矩阵中对角线元素表示被正确分类的样品，训练集、验证集实验结果若在表格中呈对角线分布，则说明模型分类准确率高。

表3 MSC－SVM模型980次分类结果混淆矩阵Table 3 Confusion matrixes of 980 plastic type labels using MSC－SVM model

表4 1D CNN模型980次分类结果混淆矩阵Table 4 Confusion matrixes of 980 plastic type labels using 1D CNN model

由表3可知，MSC－SVM模型的训练集结果均分布在对角线上，表明在此实验中分类完全准确；而其验证集除PE新生料外其他3种塑料都有分类错误的结果。表4数据未全部分布在对角线，表明1D CNN模型训练集、验证集分类结果都存在少数错误结果。综合来看，对于PP新生料的类别预测，1D CNN模型效果更好，MSC－SVM模型会较大概率将其误判为PP再生料。两种模型中，PE再生料都有一定概率被误判为PE新生料。而PE新生料几乎都可以被正确分类。

将MSC－SVM模型和1D CNN模型10次随机实验结果进行综合比较，得到表5。

表5 MSC－SVM模型和1D CNN模型准确率对比Table 5 Comparison of accuracies using MSC－SVM and 1D CNN models

由表5可知，MSC－SVM模型在训练集上表现很好，准确率为100%。在验证集上，1D CNN模型准确率为91．5%，略优于MSC－SVM模型。对于不同类别的塑料，PE再生料和PP再生料两种模型预测效果近似，PP再生料的判定准确率都不高；PE新生料的判定准确率在验证集上都达到100%；PP新生料使用1D CNN模型进行分类的准确率达100%。单次实验训练所需的平均程序执行时间，MSC－SVM模型为2．84 s，而1D CNN模型为24．55 s。可见在数据量较小的情况下，MSC－SVM模型相比1D CNN模型更快速。CNN一般在数据量大的情况下有显著优势，而在小数据集上容易发生过拟合现象。但本实验证明，只要卷积层数合理，一维卷积核的参数设置合适，加之采用一些避免过拟合的方法，也可以达到较好的准确率。而且CNN对数据预处理的要求较低，有些情况甚至无需数据预处理，亦无需考虑样本数据的特性，是一种普适方法，在近红外光谱数据分析上具有很大的应用潜力。

3 结 论

本文基于近红外光谱分析技术建立了塑料分类的MSC－SVM模型和1D CNN模型。在建立SVM模型时，比较了多种数据预处理方法对模型的影响。MSC－SVM模型在验证集上的准确率为90．8%，1D CNN模型在验证集上的准确率为91．5%，略好于MSC－SVM模型。PE新生料在验证集上的分类准确率均为100%；使用1D CNN模型判别PP新生料在验证集的准确率达100%。在本实验的小数据集上，MSC－SVM建模快速准确，而1D CNN则具有高度自学习、提取特征的能力，说明以1D CNN模型结合近红外光谱技术进行自动塑料分类可行，并可推广到其它领域的光谱分析中。