大气离子迁移率对直流线路合成电场与离子流密度影响的研究

李星举

(国网鞍山供电公司，辽宁 鞍山 114200)

电场中运动离子的速率与电场强度大小的比值被定义为离子迁移率，它是描述离子在电场中运动特性的重要物理量。同时，离子迁移率也是计算高压直流输电(HVDC)线路合成电场和离子流密度的重要参量[1-3]。

当输电线路表面的电场强度超过电晕放电起始电场强度时，导线周围的空气分子被电离成正负离子，或称为空间电荷[4-5]。在输电线路和地面之间的电场作用下，空间电荷发生定向运动，进而产生离子电流。空间电荷的电场与输电线路和地面间原有的电场相互作用，形成离子流场，或称为合成电场[6-8]。

大气离子迁移率会随环境条件，如温度、湿度和气压的变化而改变[9-11]。清华大学季一鸣[9]使用多层平行电极结构，研究了大气离子迁移率同温度、湿度和气压的关系。这一电极结构借鉴了美国国家标准局的M．Misakian[12]测量合成电场的试验平台。结果表明，正负离子迁移率均随温度、湿度、气压的增加而减小。华北电力大学刘云鹏等人[10]使用针环电极结构的测量装置也得到了类似结论。华中科技大学岳一石等人[11]使用同轴圆柱结构的Gerdien传感器测量了不同温度和不同绝对湿度下的大气离子迁移率。

离子迁移率的不同取值可能对计算结果产生影响。邹妍晖等人[13]基于上流有限元法，计算了当正负离子迁移率范围分别为1.0～2.5×10-4m2·V-1·s-1和1.2～2.7×10-4m2·V-1·s-1时，±800 kV直流输电线路下方地面合成电场和离子流密度的变化，但未考虑环境因素对导线起晕场强的影响。

本文使用一维电晕笼内合成电场的解析解和基于边界元法的双极±1100 kV高压直流输电线路合成电场的数值解，在不同大气条件下，研究了离子迁移率对直流输电线路地面合成电场和离子流密度的影响规律。

1 计算模型和方法

1.1 假设条件和控制方程

直流离子流场的建模和分析通常使用以下几个假设条件[14-16]：

a.直流离子流场是非时变场，因此场域内的各个物理量不随时间改变；

b.忽略高压导线表面的电晕层；

c.正负离子迁移率是不随电场强度改变的物理量。

在以上假设条件下，离子流场的控制方程为

(1)

E=-▽φ

(2)

J=J++J-=(ρ+K++ρ-K-)E

(3)

(4)

(5)

式中：φ为电位；E和J分别为离子流场矢量和离子流密度矢量；ρ为电荷密度；K为离子迁移率；Ri为正负离子复合系数；ε为空气介电常数，8.85×10-12F/m；e为电子电量，1.60×10-19C；Ri为正负离子的复合系数，2.2×10-12m3/s。式(1)为Poisson方程，式(3)为电磁场理论中的Ohm定律[17-18]，式(4)和式(5)是电流连续性方程。

1.2 边界条件

设高压直流导线的电压为U，远离导线的人工边界处的电压为Ua。高压导线和地面处为第一类边界条件，即电位分别是φ=U和φ=0。高压导线起晕后，其表面电场强度的大小为起晕场强E0，即为第二类边界条件，一般也成为Kaptzov假设[19-20]。上述边界条件可以写为

φ=U(在导线表面)

(6)

φ=0(在地面)

(7)

φ=Ua(在人工边界)

(8)

E=E0(在导线表面)

(9)

1.3 计算方法

本文使用直角坐标系下的边界元法(Boundary Element Method，BEM)计算高压直流导线的合成电场与离子流密度。Poisson方程和电流连续性方程分别使用边界单元和上流单元计算。

边界元法(BEM)是一种典型的边界型数值计算方法。设计算场域Ω的边界为Γ，P和Q为边界Γ上的两点，R为场域内一点。根据Green公式，得到如下的边界积分方程[21]：

(10)

式中：φ(P)为P点电位；θP为边界上P点的形状系数；rPQ为PQ两点距离；∂φQ/∂n为Q点电位在边界上的法向导数；ρR为R点的电荷密度。

将边界离散后，式(10)可以写成矩阵形式的边界代数方程[21]：

(11)

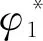
式(11)表明，边界电场强度大小E1的计算精度与电位φ2的计算精度一致，这也是边界元法优于线性单元有限元法的特点。本文在节点的上流单元中更新该节点的电荷密度。若使用三角形单元对整个场域进行剖分，在任一三角形计算单元中，当节点的电场强度方向在该点夹角的延长线内，则这样的计算单元为该节点的上流单元[19]。将式(4)和式(5)代入式(3)，可以得到：

(12)

(13)

根据式(12)和式(13)，该节点的电荷密度由其电场强度和三角形内另外2个节点的电荷密度更新。

近年来，生态旅游业发展火爆，各地都在积极开发生态旅游事业，取得了一定的成效，生态旅游已经成为旅游业可持续发展的有效途径。在发展生态旅游业的过程中，也遇到了一些问题和阻碍，没有有效发挥生态旅游对环境保护的积极作用，对此，还需要进一步提升认识，积极组织开展生态旅游，推进生态旅游发展模式的不断优化，才能促进生态旅游和环境保护的协同发展。

1.4 算法的验证

按边界元法在同轴圆柱电极中加以验证。设内外电极的半径分别为R1和R2，电位分别为φ1=U和φ2=0。若场域内空间电荷密度为零，则圆柱电极间的电位分布可使用Laplace方程描述，电极间场强解析解为

(14)

若圆柱间空间电荷密度为ρ0，如图1所示，则电极间的电位分布使用式(1)描述，电场强度的解析解为

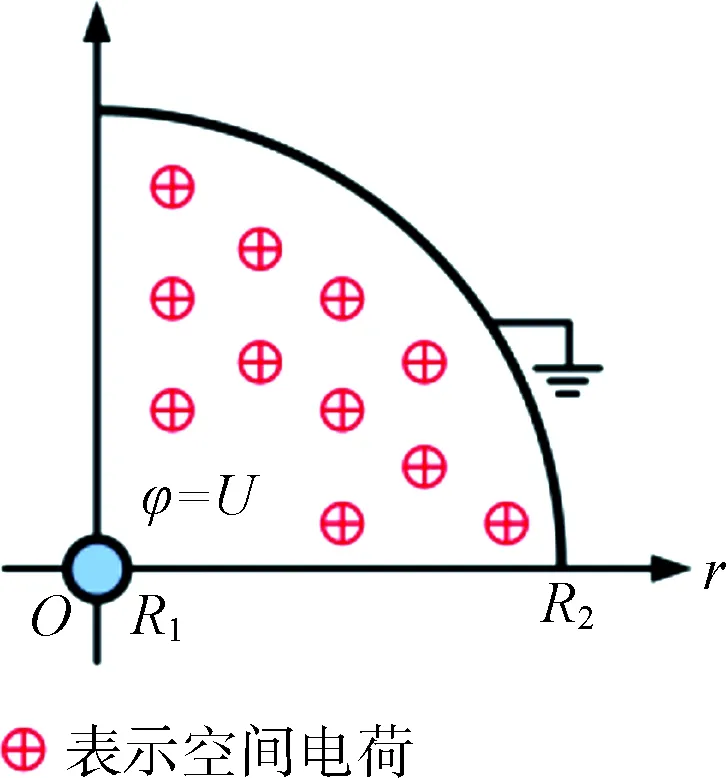
图1 一维圆柱电极间的电场示意图

(15)

本文使用的电晕笼计算参数为R1=5 mm，R2=0.4 m，U=45 kV，ρ0=2.0μC/m3，分别根据式(14)的解析解和边界元法计算圆柱电极间的电场分布，结果如表1所示。在边界元法计算过程中，内外圆柱电极分别使用60个和120个边界元。由表1可知，使用BEM计算得到的电极表面处的离子流场是精确的，相对误差不超过0.2%，验证了算法的准确性。

表1 使用解析解和BEM计算电极处的电场结果

2 迁移率对一维合成电场与离子流密度的影响

电晕笼是研究高压输电线路合成电场、离子流密度或其他电磁环境参数的常用试验装置，由中间的测量段和两端的屏蔽段组成[22-23]。高压导线同心地置于电晕笼内，因而圆形电晕笼测量段内的合成电场可视作一维分布。在1.1的假设条件下，一维圆柱电极间的合成电场与离子流密度的控制方程可简化为

(16)

J=ρKE

(17)

▽·J=0

(18)

圆柱电极间一维合成电场的边界条件为式(6)、式(7)和式(9)。

在以上控制方程和边界条件下，合成电场的解析解可写为式(19)、式(20)[14]。计算流程如图2所示。

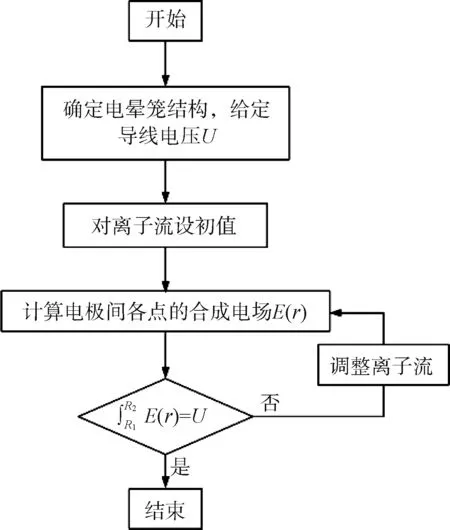
图2 迁移率对一维合成电场影响的计算流程图

(19)

(20)

根据文献[11]，在绝度湿度为9 g/m3时，环境温度从10 ℃增加到40 ℃时，正负离子迁移率变化范围分别约为1.05～1.30×10-4m2·V-1·s-1和1.25～1.65×10-4m2·V-1·s-1。文献[10]研究表明，当温度在16 ℃、相对湿度为50%、气压从64 kPa变为101 kPa时，正负离子迁移率分别为1.20～1.75×10-4m2·V-1·s-1和1.5～2.3×10-4m2·V-1·s-1。由于文献[10]中大气离子迁移率的研究范围更大，因此本文在后续计算中，所使用的环境参数和大气离子迁移率的变化范围与文献[10]的结果一致，如表2所示。

表2 气压对空气相对密度和迁移率的影响

环境条件变化后，导线起晕场强的改变同样需要考虑。根据Peek公式，起晕场强表示为

(21)

(22)

式中：α和β为经验系数，对于正极高压直流导线，α=33.7，β=0.240，对于负极导线，α=31.0，β=0.308[24]；m为粗糙系数，输电线路一般取0.4到0.6；r为导线半径；δ为相对于常温常压下的空气密度；p为环境气压，p0为标准大气压，101 kPa；T为环境温度，T0为常温293 K。

根据文献[10]，大气正负离子迁移率随气压的变化如表2所示；由式(22)计算得到δ的范围为0.642到1.01。在本文中m的取值为0.5；高压导线电压U取55 kV，半径R1取0.5 cm；电晕笼半径R2取40 cm。基于以上计算条件和方法，得到电晕笼处合成电场与离子流密度的结果如图3和图4所示，电极间合成电场与离子流密度的结果如图5和图6所示。以下结果包括两种计算条件：环境条件变化导致大气离子迁移率K与导线起晕场强E0都发生变化，以及只对离子迁移率的取值做改变。

结果表明，当气压由标准大气压减小到0.63倍标准大气压即64 kPa时，电晕笼处的正极性合成电场由50.1 kV/m增加到93.1 kV/m (增强85.8%)。负极性合成电场由-52.4 kV/m变为-93.3 kV/m (变化78.1%)。这是因为气压减小时，正负离子迁移率增加，导线起晕场强降低，导线电晕程度增强。由图3可知，电晕笼处合成电场的增加量随离子迁移率的增加而减小，说明了式(19)和式(20)的非线性特征。如果只人为改变离子迁移率的取值而保持导线起晕场强不变，则电晕笼处合成电场几乎不随大气离子迁移率改变，始终为50.1 kV/m和-52.4 kV/m。以上计算表明，电晕笼处合成电场的增加几乎全部来自导线起晕场强的降低。

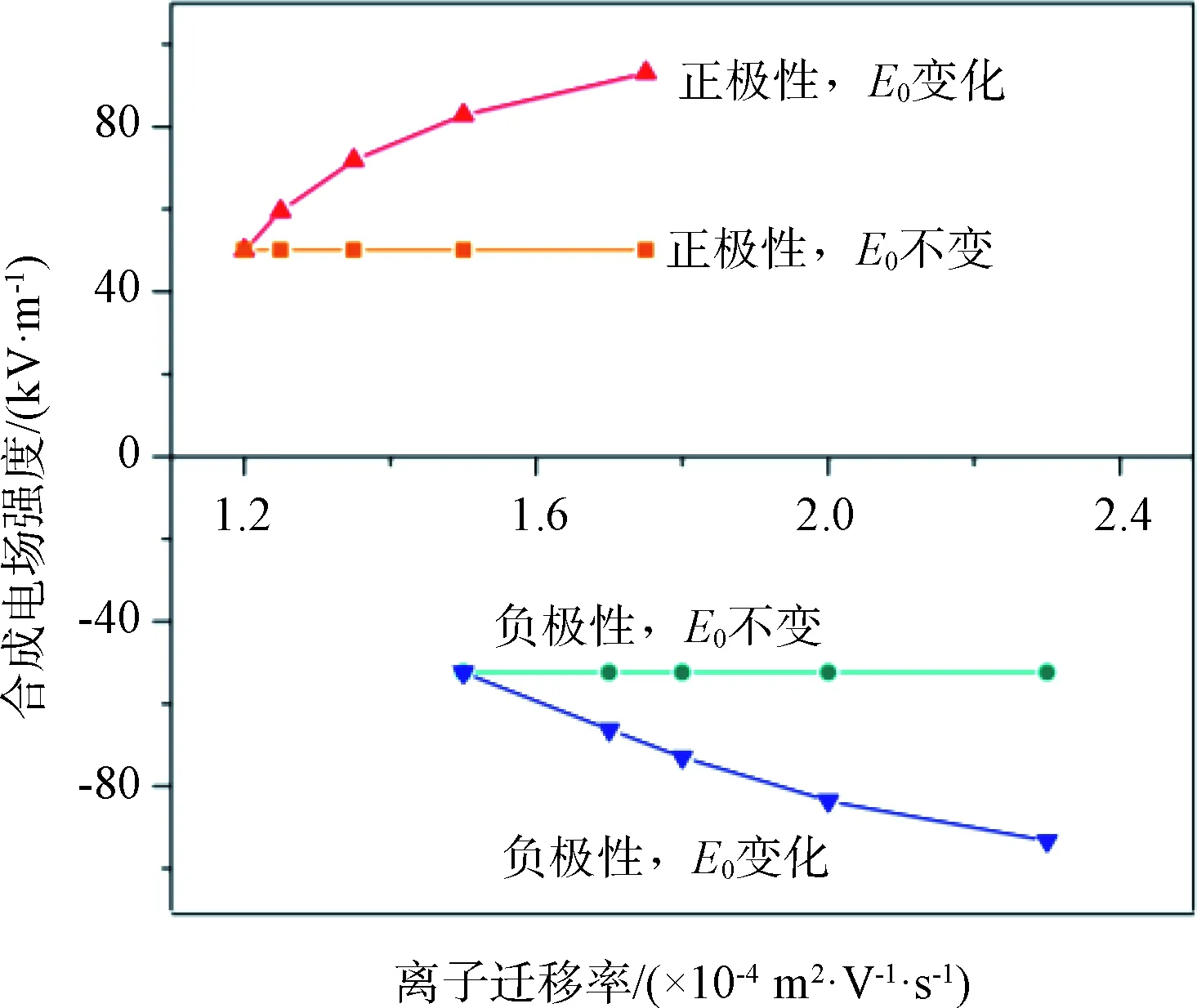
图3 迁移率对电晕笼处合成电场的影响

对于电晕笼处离子流密度的变化，由图4可知，气压的降低导致大气离子迁移率的增加以及导线起晕场强的降低，正负极性离子流密度的增加幅度分别为6.15倍和5.54倍。此外，如果只改变离子迁移率而令导线起晕场强不变，正负离子流密度增加幅度只有0.46倍和0.53倍；此时离子流密度随迁移率呈线性变化。

图4 迁移率对电晕笼处离子流密度的影响

由图5和图6可知，当气压减小导致大气离子迁移率增加以及导线起晕场强降低时，导线附近合成电场减弱，电晕笼附近合成电场增强，离子流密度在整个场域增加明显。如果只有迁移率K取值改变而起晕场强E0不变，场域内合成电场分布几乎不变，离子流密度随迁移率近似呈线性变化。

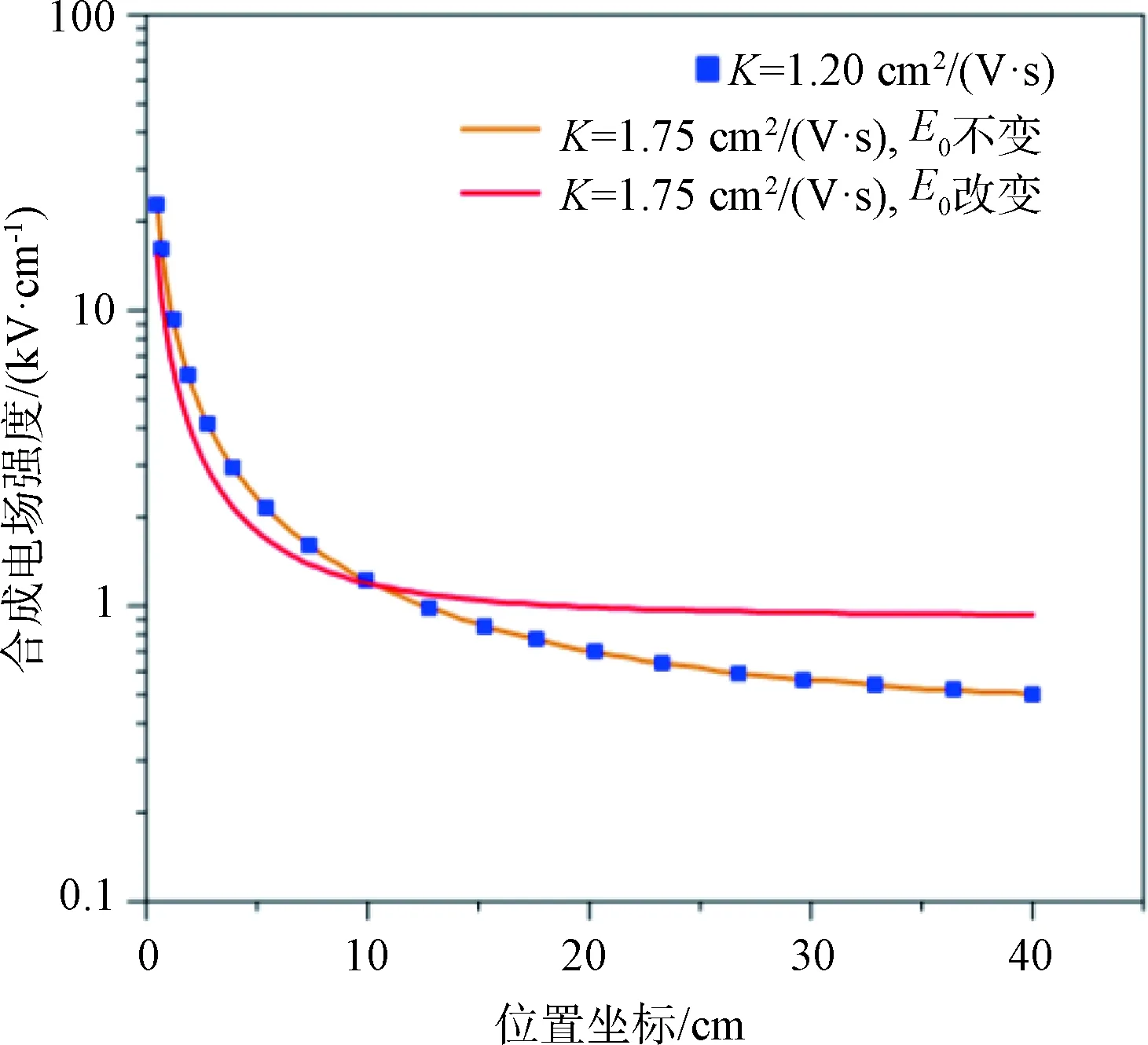
图5 迁移率对电晕笼内合成电场的影响(正极性)

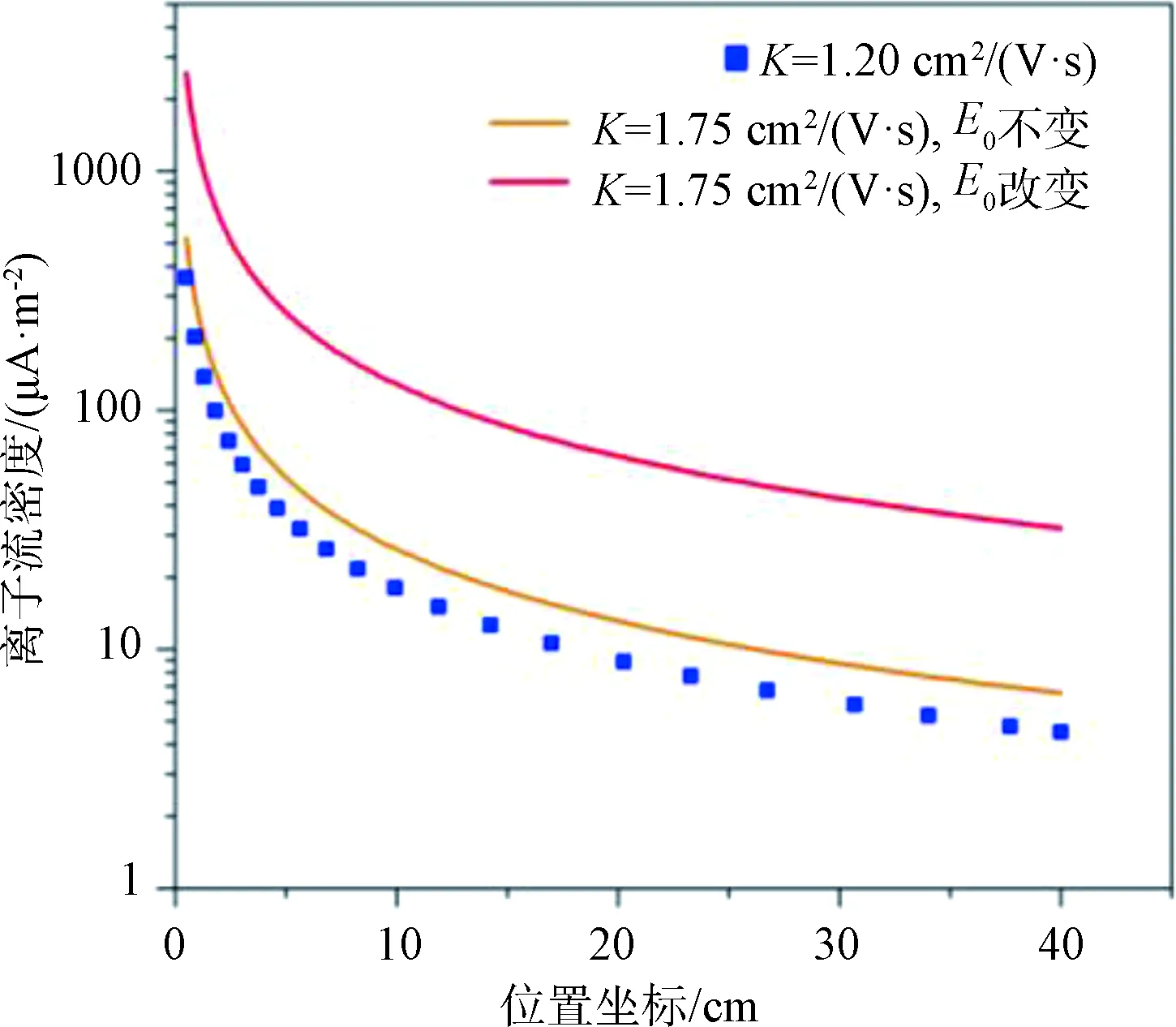
图6 迁移率对电晕笼内离子流密度的影响(正极性)

综上，当离子迁移率增加约一半，同时起晕场强降低33%，电晕笼处合成电场增强约80%，离子流密度增加约6倍。与大气离子迁移率相比，导线起晕场强对合成电场和离子流密度的改变占主导。

3 迁移率对输电线路合成电场与离子流密度的影响

使用±1100 kV双极8分裂直流导线对地的电极结构，研究离子迁移率的变化对地面处的合成电场与离子流密度分布的影响。计算场域为边长200 m×100 m的矩形区域，杆塔置于矩形区域的中心正下方。取每极高压导线中心对地高度为27 m，极间距为28 m，即正负极导线中心坐标分别为±14 m，导线分裂间距为0.50 m，子导线直径为4.74 cm。

矩形边界电位取为0 V。导线起晕场强由式(21)计算，正负极导线粗糙系数m取为0.43。根据文献[10]，当气压从101 kPa降低为94 kPa和84 kPa时，大气离子迁移率与导线起晕场强同时变化。导线在101 kPa时起晕场强取±17.0 kV/cm，根据Peek公式，后两种气压时起晕场强分别为±15.9 kV/cm和±14.3 kV/cm，分别降低了6.5%和15.9%。使用边界元法计算地面处的合成电场和离子流密度，结果如图7和图8所示。

由图7和图8可知，由于气压的降低，大气离子迁移率和导线起晕场强发生同步变化后，地面合成电场与离子流密度都增强。计算表明，当正负离子迁移率从1.20×10-4和1.50×10-4m2·V-1·s-1增加至1.25×10-4和1.70×10-4m2·V-1·s-1，地面处合成电场平均增加14.7%；正负离子迁移率增加至1.35×10-4和1.80×10-4m2·V-1·s-1，合成电场平均增加37.3%。对于地面处离子流密度，增加的幅度分别为0.53倍和1.5倍。

图7 迁移率对直流线路下方地面合成电场的影响(离子迁移率单位：m2·V-1·s-1)

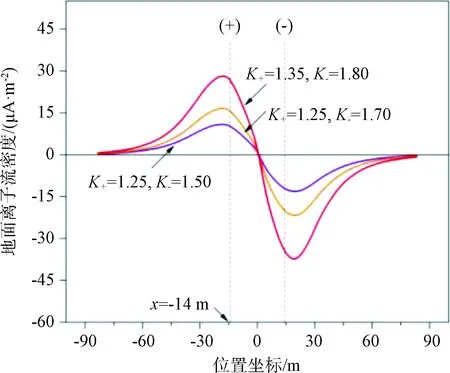
图8 迁移率对直流线路下方地面离子流密度的影响(离子迁移率单位：m2·V-1·s-1)

综上，如果气压进一步降低导致大气离子迁移率的增加和导线起晕电压的降低，地面处合成电场可能超过电磁环境限值30 kV/m[25]。此时应修正杆塔结构参数，例如使用直径更大的输电导线。

4 结论

本文使用一维圆柱电极结构和二维双极输电线对地结构，研究了大气离子迁移率的改变对高压直流线路合成电场和离子流密度分布的影响，取得了如下结论。

a.环境条件的改变使得大气离子迁移率和导线起晕场强都变化，进而改变电晕笼处的合成电场和离子流密度。与大气离子迁移率相比，导线起晕场强对合成电场和离子流密度的改变占主导。

b.一定大气条件下，正负离子迁移率变化范围分别为1.20～1.75×10-4m2·V-1·s-1和1.5～2.3×10-4m2·V-1·s-1时，电晕笼处的合成电场增强约80%，离子流密度增加约6倍。

c.一定大气条件下，正负离子迁移率变化范围分别为1.20～1.35×10-4m2·V-1·s-1和1.5～1.8×10-4m2·V-1·s-1时，±1100 kV双极输电线路下方地面处的合成电场平均增强0.53倍，离子流密度平均增加1.5倍。

d.若计算时仅改变迁移率的取值，合成电场变化不大，离子流密度随迁移率近似呈线性变化。