杠杆率水平对城市商业银行风险承担的影响

陈燕玲,凌 峰

(安徽大学经济学院, 安徽 合肥 230601)

2008年金融危机的爆发加速了《巴塞尔协议Ⅲ》的出台，杠杆率作为银行业的监管工具开始进入国际视野。与此同时，我国也出台了相应的监管政策——《商业银行杠杆率管理办法》(以下简称《办法》)，正式引入具备无风险敏感性特点的杠杆率作为我国商业银行的监管指标，以达到防范风险的目的。2015年，原银监会又对该《办法》进行了修订，此次修订对杠杆率分母作出相应调整，相对降低了银行达标压力。

自1995年第一家城市商业银行(以下简称“城商行”)成立以来，经历了20多年的改革发展，全国城商行数量已发展至134家，行业总体规模扩大近40倍，从业人员数量接近30万，网点遍布全国各地，体系日趋完善，在促进地方城市基础设施建设、给予中小微企业贷款支持和健全地方金融体系方面发挥着重要作用。但是，近年来，由于一味扩张规模以及国内经济增速逐渐放缓等原因，城商行经营管理中的潜在问题不断浮出水面，不良贷款不断增加，资产质量承压增大，信用风险、流动性风险等各类风险陆续显现，风险事件不断发生。2019年以来，相继发生了包商银行被接管、锦州银行重组和营口沿海银行发生挤兑等风险事件，打破了同业间的刚性兑付，市场主体对城商行的不信任情绪显著上升。信用风险和流动性风险相互交融，层层传导。在信息不对称背景下，这使得声誉风险和流动性风险事件爆发的概率加大，导致城商行的风险管控面临前所未有的挑战。因此，研究杠杆率水平对城商行风险承担的影响，对于促进城商行稳健经营、完善杠杆率监管体系、防范银行业系统风险有着重要意义。

一、文献综述

(一)国外文献综述

对于杠杆率与银行风险承担之间的关系，国外有两种不同的意见。一种观点认为杠杆率监管有助于银行稳健经营。Jarrow认为，杠杆率监管对银行真实风险的识别更加可靠，可以有效地控制银行风险[1]。随后，Dermine运用理论模型证实，当银行资产价值存在信息不对称时，杠杆率监管有利于增强银行抵御风险的能力[2]。Smith等学者利用2005—2014年655家欧盟银行的面板数据进行实证分析，得出“对于高杠杆银行，杠杆率的引入可以有效降低其破产风险”的结论[3]。然而，另一种观点认为杠杆率监管会对银行产生不利影响。Baker和Jeffrey以美国银行的非平衡面板数据为研究对象，实证分析杠杆率监管与银行风险之间的关系，研究发现杠杆率监管会导致银行风险上升[4]。Janda和Kravtsov使用2007年之后15家银行8年的数据进行实证研究，分析金融危机发生后的一个经济周期内杠杆率对银行风险承担及其业务分布的影响，研究发现，杠杆率水平的提高会降低贷款数量，影响银行的营利能力，进而可能会导致银行的风险偏好增加，最终增加银行风险[5]。

(二)国内文献综述

《巴塞尔协议Ⅲ》和《办法》颁布后，国内学者围绕杠杆率监管与商业银行风险之间的关系进行了广泛研究。由于模型设定、研究样本或研究对象不同，观点较为多样，主要分为三种。一些学者认为杠杆率监管可抑制风险，如袁辊等、冯乾等、陈伟平等、张庆君等学者利用不同年份商业银行的经营数据进行实证分析，均得出相似的结论，即杠杆率监管的实施可以有效约束银行的风险偏好，有助于银行自有资本持有比例的提升，有效控制了银行风险[6-9]。一些学者则得出完全相反的结论，如陈梦雯等[10]、靳玉英等[11]学者利用理论模型与国内上市银行经营数据相结合的方式得出以下结论：杠杆率的引入会促使银行选择高风险高收益的资产，导致银行对信贷资产的逆向选择，造成银行高风险资产比例上升，从而增加银行承担的风险。还有一些学者认为，在不同的条件下，杠杆率水平对商业银行风险承担的影响不相同。黄海波等基于线性规划方法分析了商业银行同时受到杠杆率和资本充足率约束时的行为变化，发现杠杆率的引入虽然对顺周期性有缓释影响，但也降低了风险敏感度，导致监管资本套利的发生，两种指标共同监管所起的作用可能互相补充，也可能互相抵触[12]。

综上所述，虽然国内外已有相关文献为本文研究提供了重要理论依据，但仍存在以下不足：研究样本大多集中于上市银行等体量较大的银行群体，对体量较小的城商行等银行群体缺乏研究，或虽偶有涉及，也仅是选择数家上市城商行作为子样本进行异质性分析，分布范围仅限于几个经济发达省市，呈数量少、范围窄的特点。因此，本文选取45家城商行作为研究样本，涉及全国23个省(区、市)，从城商行角度对杠杆率监管的影响进行研究，结果具有一定的可靠性。该研究一方面完善了国内文献在杠杆率监管方面的研究，另一方面也有助于监管部门对城商行进行监管。

二、研究设计

(一)模型设计

为研究杠杆率监管对城商行风险承担的影响，本文以城商行风险承担为被解释变量，杠杆率指标为核心解释变量，构建动态面板数据模型

Zit=β0+β1Zi,t-1+β2LEVi,t+β3LEVi,t-1+

其中，i表示城商行，t表示年份。被解释变量为Zit，核心解释变量为杠杆率当期值LEVi,t，控制变量为资产总额的自然对数(ASSETi,t)、 总资产增长率(GROWTHi,t)、净资产收益率(ROEi,t)、存贷比(LDRi,t)、成本收入比(CIRi,t)、资本充足率(CARi,t)、国内生产总值同比增速(GDPi,t)，vi是城商行固定效应，εi,t是随机扰动项。本文着重关注系数β2的符号及显著性。

(二)变量选取与说明

1.被解释变量：城商行风险承担。根据已有的文献可知，学者通常将Z值、不良贷款率、预期违约概率、股价波动率、存贷比、资产资本比率、加权风险资产占比等作为衡量商业银行风险承担的指标。由于部分数据无法获得和部分样本银行尚未上市导致数据缺失较多等原因，本文借鉴以往的处理方法，利用Z值表示银行承担的风险大小[13]。Z值的计算方法为

其中，ROAit表示第t年样本银行的总资产净利率的均值，σit表示总资产净利率的标准差，CAit表示资本资产比率。Z值与商业银行风险承担之间呈反向关系，即Z值越大表明商业银行承担的风险越小。

2.核心解释变量：杠杆率指标当期值(LEVi,t)。2015年监管部门对《办法》进行了修订，调整了杠杆率的计算方式，因此本文选用修订后的《办法》中规定的商业银行杠杆率作为LEVi,t的代理变量。

3.控制变量。为了提高研究结论的准确性，本文选用一系列的控制变量，尽量避免错误、遗漏的出现。在以往研究的基础上，选择如下银行特征变量：代表银行规模的资产总额的自然对数(ASSETi,t)、代表成长性的总资产的增长率(GROWTHi,t)、代表营利能力的净资产收益率(ROEi,t)、代表流动性的存贷比(LDRi,t)、代表运营效率的成本收入比(CIRi,t)、代表资本水平的资本充足率(CARi,t)。由于城商行在不同区域发展情况存在较大差异，故选取各城商行所省(市、区)年度GDP同比增长率(GDPi,t)代表宏观经济变量，在一定程度上控制异质性影响(表1)。

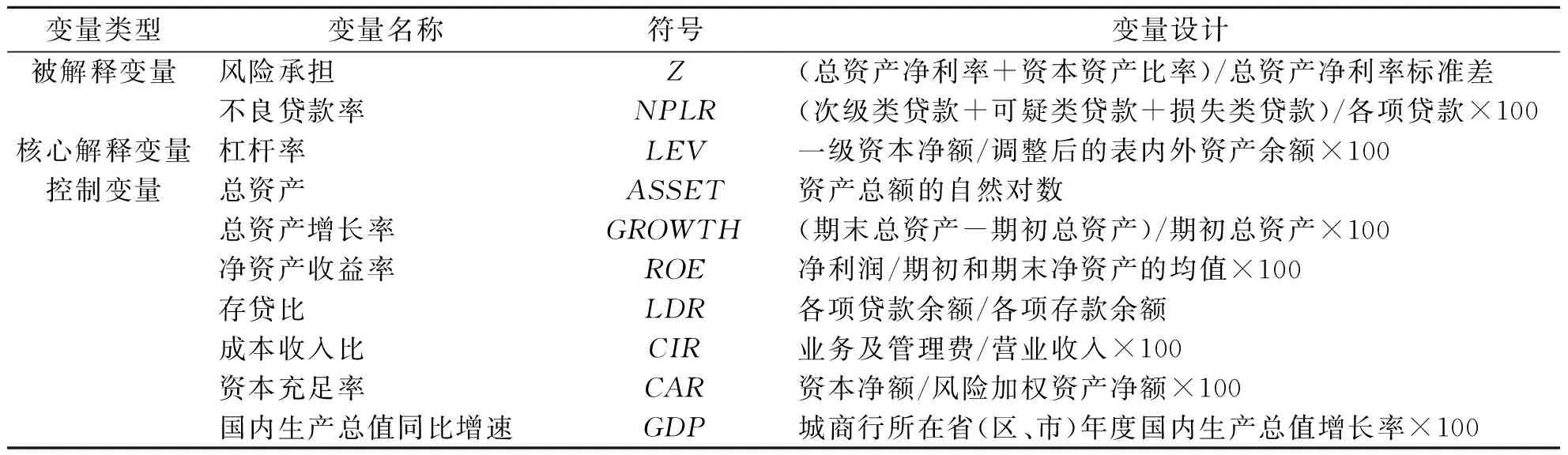
表1 变量说明

(三)样本选取与描述性统计

依据数据的可得性、代表性与真实性，本文选取2015—2019年45家城商行数据作为研究样本。若无特别说明，本文所有数据来源为iFinD数据库、Wind数据库和各城商行年报，部分指标根据以上来源数据计算得出。

表2描述了45家城商行主要变量的总体情况。Z值的最大值为851.89，最小值为6.701，标准差为108.535，说明各城商行间风险承担存在非常大的差异。此外，总资产增长率、净资产收益率、成本收入比和国内生产总值同比增速的标准差均大于5，说明各城商行在这4个指标上均存在较大的差异。解释变量杠杆率最大值为11.080，最小值为2.32，均值为6.285，45家银行5年间仅有两次数值低于4，表明城商行总体杠杆率指标表现良好，进一步说明杠杆率监管在当前城商行中基本得到落实。

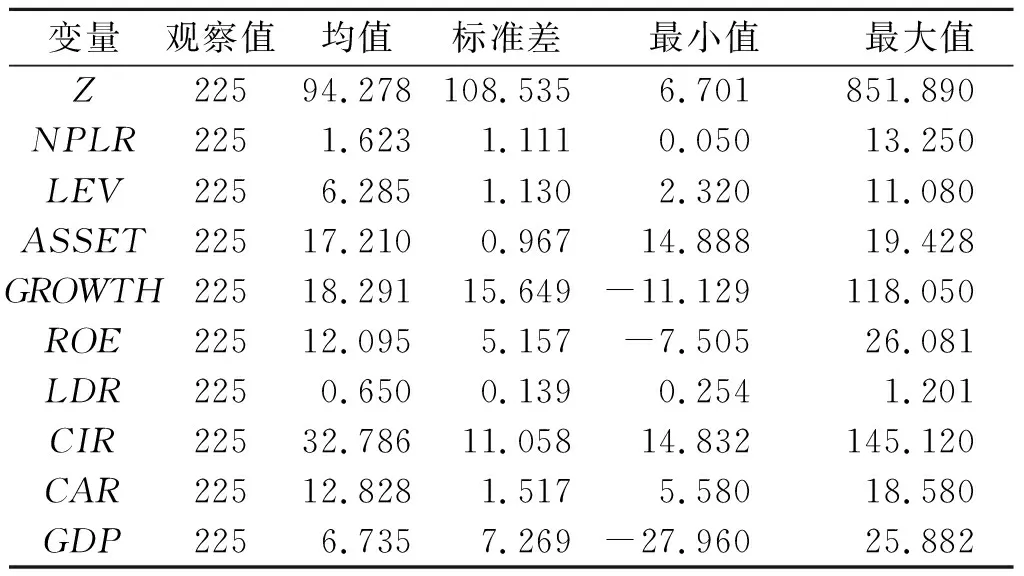
表2 变量描述性统计

三、实证分析

(一)方法

由于本文构建的是含有被解释变量滞后项的动态面板模型，故使用FE模型、RE模型、POOL回归等进行分析都可能会产生内生性问题，而工具变量法是缓解甚至消除内生性问题的一种有效方法，因此，可以采用广义矩估计对当前动态模型进行估计。广义矩估计通常分为两种：差分广义矩估计(DIF-GMM)和系统广义矩估计(SYS-GMM)。差分广义矩估计是先对模型作一阶差分从而消除个体效应，并将所有可能的滞后变量作为工具变量，其缺点在于如果被解释变量的持续性很强，就可能会导致弱工具变量问题；但将差分值与水平值相结合的SYS-GMM可以克服此问题，提高估计效率。综上所述，本文拟选取SYS-GMM方法对样本数据进行回归分析。

(二)相关性检验与结果分析

1.相关性检验。为避免回归模型中因各解释变量之间存在高度相关性而造成多重共线性问题，本文先对主要解释变量进行相关性检验。从表3可以看出，主要解释变量之间基本不存在高度相关的情形。

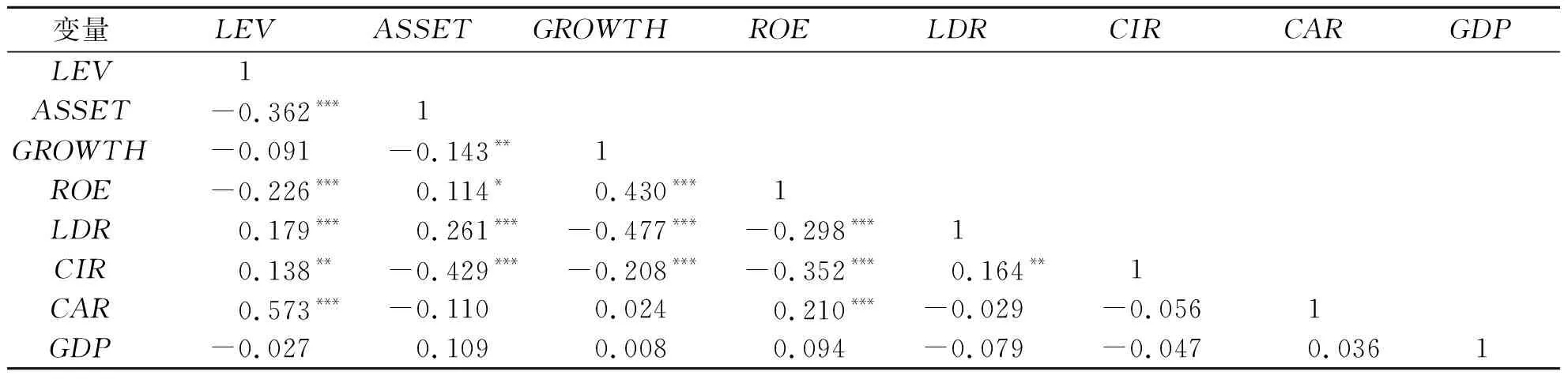
表3 相关性检验

2.结果分析。从表4可以得出如下结论：

表4 杠杆率水平对城商行风险承担的影响

(1)Z值的滞后一期对于当期的影响在1%的置信水平下呈显著正相关关系。由于Z值与银行风险承担呈反向关系，说明上一期的银行风险越小，本期的风险也会越小。

(2)杠杆率在1%的置信水平下呈显著正相关，因此可以证实在保持其他变量不变的情况下，提高杠杆率将会降低城商行承担的风险。具体而言，杠杆率每增加1个单位，商业银行风险将下降6.42个百分点，这与袁辊等、Smith等、陈伟平等、张庆君等的研究结论基本一致。本文研究结论说明，引入最低杠杆率要求能够有效控制城商行的风险承担水平。可见，杠杆率监管十分必要。

(3)城商行自身特征的控制变量对其风险承担的影响有差异。城商行成本收入比的提升、资产规模的扩张及其扩张速度的加快显著提高了其风险水平，资本充足率和存贷比的提升显著增强了城商行抵御风险的能力，以上与前人的结论基本一致；而城商行净资产收益率的提升降低了银行的风险，这与常理不符。可能的原因是，高风险高收益的业务对自身营利能力强的银行诱惑较小，因此银行的风险也会较小。

(4)宏观上GDP的提高对城商行抵御风险有促进作用，但统计效果不显著。此外，Sargan检验的P值为0.610 3，大于0.1，说明工具变量的选取是合理的；AR(2)的P值为0.312 7，大于0.1，说明不存在扰动项二阶自相关。

3.城商行异质性分析。众所周知，相同的监管政策对于不同性质的银行产生的效果可能并不一致，因此需要对城商行分类然后进行异质性分析。由于城商行是以营利为目的商业银行，故本文从总资产净利率、净资产收益率、银行利润率三个维度对总样本进行聚类分析，将其分成两个子样本，分别是经营绩效较好的城商行和经营绩效较差的城商行，并将其定为panel1和panel2，依次进行回归分析。表5所示的回归结果显示，LEV的回归系数分别是0.096 2和0.035 4，回归系数均为正，但大小和显著性有差异，说明城商行的异质性会使得杠杆率水平对不同城商行的风险承担产生不同的影响。

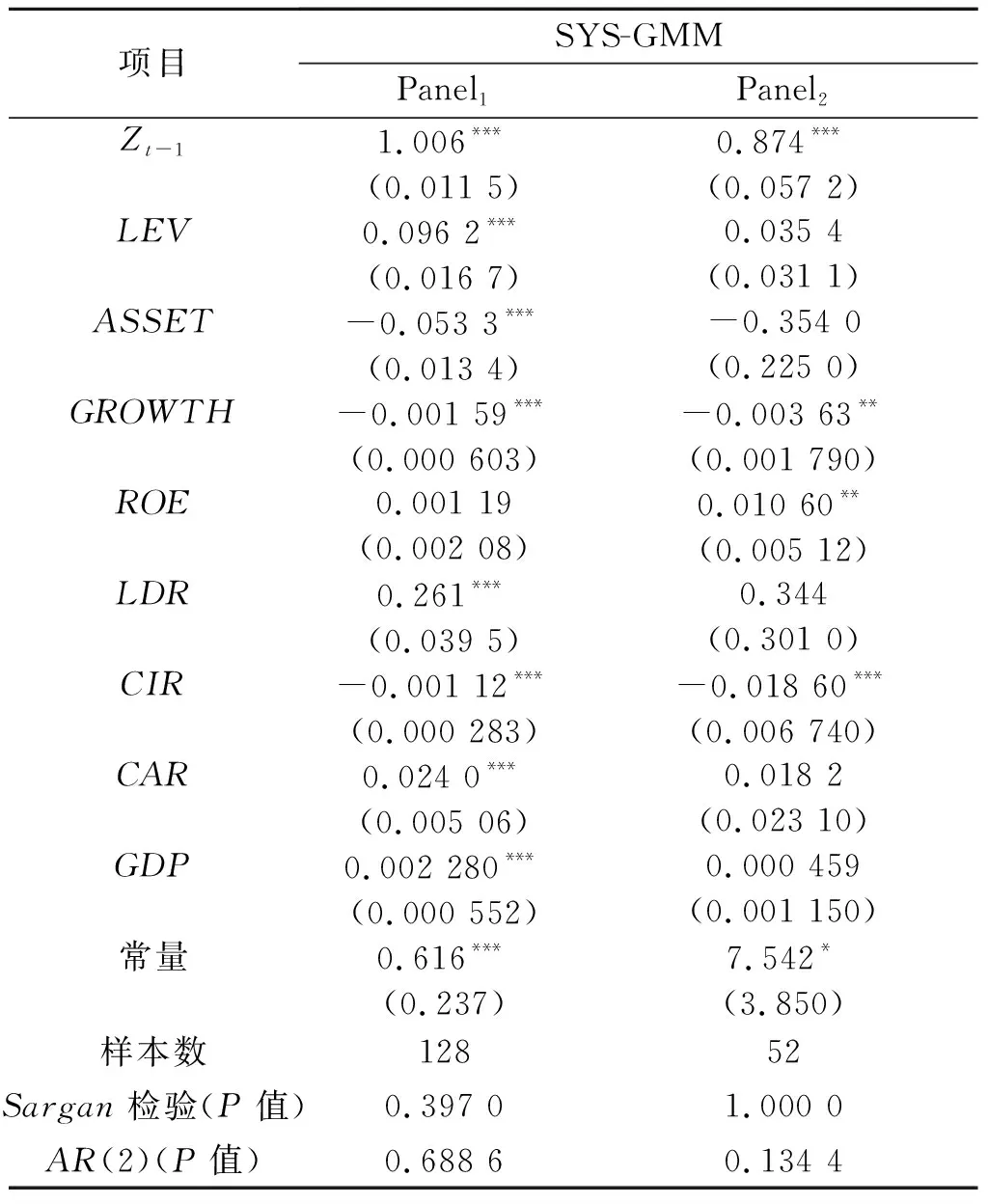
表5 杠杆率水平对异质性城商行风险承担的影响

具体而言，最低杠杆率要求对经营绩效较好的城商行风险缓释作用较大且效果显著，对经营绩效较差的城商行风险缓释作用较小且效果不显著。

(三)稳健性检验

为验证结论的有效性，本文采用两种方法进行稳健性检验。

1.数据不变，使用不同模型进行估计。本文依次采用POOL、FE、RE三种静态模型进行稳健性检验。由表6可知，三种估计方法中杠杆率的回归系数均为正，同SYS-GMM估计结果一致，且除了混合回归模型的显著性不及SYS-GMM外，其他两种估计方法的显著性均同SYS-GMM保持一致，因此该稳健性检验支持SYS-GMM的结果。

2.模型不变，替换被解释变量进行估计。针对银行风险承担度量指标，在控制其他变量保持不变的前提下，利用不良贷款率NPLR代替Z值，再对原模型进行SYS-GMM检验。由表6可知，LEV在5%的置信水平下与银行风险承担呈显著负相关关系，同样得出了杠杆率有助于降低城商行风险的结论，这与以Z值为被解释变量的回归结果无实质性的差别，再次证明本文的回归结果具有可靠性。

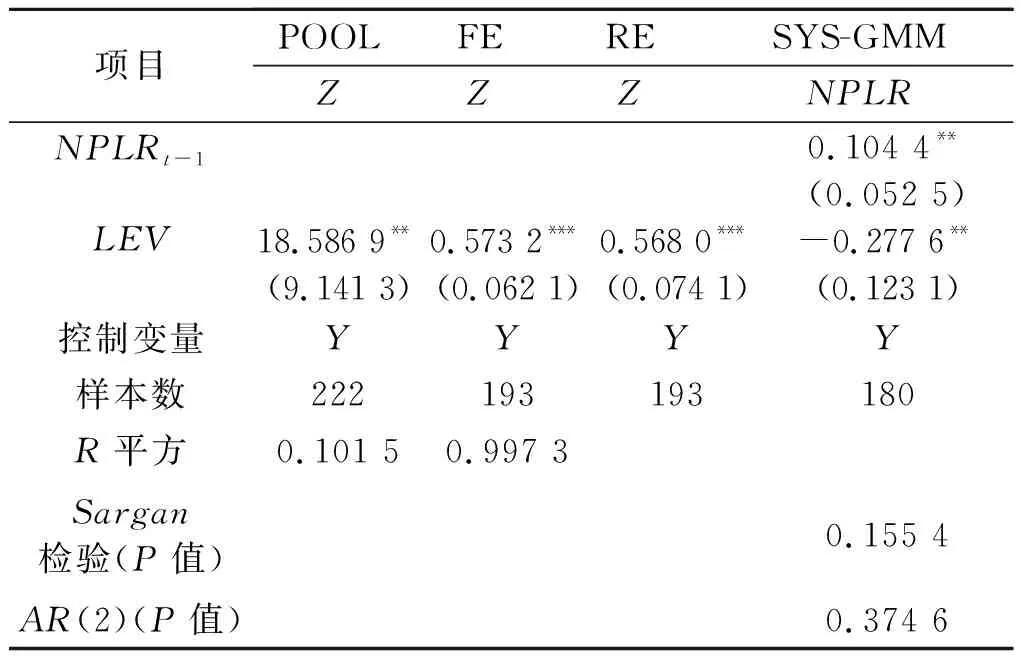
表6 杠杆率水平对城商行风险承担影响的稳健性检验

四、研究结论及建议

(一)结论

本文在杠杆率指标已被纳入我国商业银行监管体系和城商行风险频发的背景下，采用2015—2019年45家城商行的数据，基于SYS-GMM模型探究了杠杆率水平对城商行风险承担的影响。研究结果表明，最低杠杆率要求降低了城商行的风险承担水平，并且该结论通过了多项稳健性检验，这证明了我国监管部门实施《商业银行杠杆率管理办法》的正确性和前瞻性，有助于城商行控制财务杠杆累积，增强自身风险抵御能力。研究结果还显示：微观层面上，城商行自身特征变量对风险承担的影响具有差异性，银行成本收入比、资产规模扩张及其扩张速度的提升会导致银行风险的增加，而银行净资产收益率、存贷比和资本充足率的提升可以降低银行风险；宏观层面上，GDP同比增长率的提升可以提高银行抗风险的能力，但统计意义不显著；此外，通过异质性分析发现，最低杠杆率要求对经营绩效较好的城商行具有显著降低风险的作用，但对经营绩效较差的城商行降低风险的作用较弱，且统计意义不显著。

(二)建议

基于上述研究结论，本文提出四点建议。

1.监管部门需要制定更为严格的城商行杠杆率信息披露制度，提高杠杆率透明度，防止城商行资产负债表过度扩张，尽量避免其发生资本监管套利的现象。

2.由于杠杆率对城商行的监管具有异质性，不同性质的城商行存在客观差异，监管部门应该区别对待，采用差别监管标准，避免采用一刀切的监管方式。同时，城商行也应该积极配合监管部门，与监管部门保持一致，共同营造一个良好的监管环境。

3.监管部门应采用稳杠杆策略，减小去杠杆所引起的城商行体系震动，并将杠杆率与资本充足率相结合，共同控制城商行的高杠杆风险和资本风险，以达到稳定城商行体系的目的。

4.随着金融科技的发展和银行业务、产品的进一步创新，银行面临的风险和产生的问题愈加复杂，给银行风险监管带来挑战，监管部门需结合银行的自身特征变量进一步完善监管体制，以便于更好地控制城商行的风险。