多UAV/MALD 协同下战机生存力评估模型

宋海方，刘 洁，汪时交，周弘哲

（解放军92925 部队，山西 长治 046000）

0 引言

战机要完成作战任务，首先要具有一定的生存力［1］。战机生存力的分析包括敏感性和易损性两部分，对于进入现役的飞机而言，主要是通过战术手段降低其敏感性的方式来提高其生存力。战术手段包括使用电子对抗、执行战术机动以及己方体系支援等。

近几年，随着UAV 和MALD 等技术和装备的发展［2］，有人驾驶飞机与多架UAV 或MALD 的协同作战成为一种新的战术方法。例如，美军从20 世纪90 年代开始研制MALD，经过十几年的发展，2011 年完成了从运输机上投放MALD 来保护己方作战飞机的试验，一架运输机一次可以投放数百个MALD［3］。与MALD 作用类似，UAV 也可以通过多架集群的方式与战机协同作战。MALD 或UAV 通过模拟己方战机的运动及信号特征来保护己方飞机，凭借其长航时、高机动、自主空战和组网能力，提高战机在高威胁环境中执行作战任务的能力，这是对传统作战方式的一种创新。

对战机在多MALD 或多UAV 协同下的生存力评估成为一个重要的问题。目前对飞机生存力的评估主要是对单机生存力的分析，如文献［4］将灵敏度分析应用到飞机生存力设计，为飞机生存力设计中的初始变量范围缩减提供了依据；文献［5］对典型作战场景中的隐身飞机敏感性因素进行了组合分析研究，对隐身飞机敏感性缩减和方案设计改进有一定的参考意义。文献［6-7］将单机对抗情形进行了拓展，从体系对抗和有伴飞诱饵协同情形下的飞行器作战效能进行了研究，分别用探测概率和突防概率对作战效能进行了评估，没有考虑战机的暴露时间同自身生存力的关系。

排队论［13］是一种典型的基于时间的效能评估模型。文献［14-15］基于排队论分析了侧重火力纵深和火力密度两种情形下的作战效能。但是在使用排队论对生存力进行评估时，需要注意两点：一是飞机的生存力本身也是飞机相对威胁暴露时间的函数。例如，文献［14-15］用基本相同的排队模型，得出了两个截然相反的结论：文献［14］指出，对于探测和导弹命中精度较低的系统，应采用协同防御、侧重火力密度的防空模式；对于探测系统和导弹命中精度较高的系统，应该采用侧重火力纵深、多级防御的模式。而文献［15］的结论恰好与此相反，原因就在于没有考虑飞机生存力是时间的函数，各自使用了不同的、与时间无关的导弹命中概率函数。二是地面防空系统如果没有空闲时间或通道来处理来袭飞机，则飞机可以直接通过该防空区域而不是“等待”防空武器的跟踪和射击等“服务”，换句话说，用于分析飞机生存力的排队模型是无等待的服务系统。

本文对战机在突防或对地攻击过程中，受地面防空系统的威胁，对战机在多MALD 或者多UAV协同下的生存力模型进行研究，首先建立了飞机生存力的等效时间模型，其次建立了基于M/M/1/N 排队论的飞机生存力评估模型，最后借助算例，论述了MALD/UAV 投放速率、地面防空单元数目和战机自身敏感性等参数之间的关系。

1 飞机生存力的等效时间模型

战机在突防作战中的生存过程可以用Markov链进行建模，战机的生存力函数可以基于寿命过程建模。战机途径某威胁单元生存力随时间的变化关系可以表示为［9］

推论：分析战机通过各种战术对抗措施降低λ对生存力的影响，等价于分析减少战机暴露时间t2-t1对生存力的影响。

2 基于M/M/1/N 模型的战机生存力评估模型

现代防空导弹作战单元都具有多目标打击能力。考虑在单一地面防空系统的威胁下，作战飞机在多架UAV 或者MALD 的协同支援下进攻，对攻防两端的模型假设如下：

1）UAV 或MALD 的发射过程是平稳的，且服从参数为ξ 的Poisson 过程，即在t 时间内，对防空单元攻击m 次的概率为

由于Poisson 过程和指数分布的等价性，式（5）可以等价表示为两架UAV/MALD 的出动时间间隔服从参数为ξ 的负指数分布。

2）假设UAV 或MALD 能够完全模拟战机的信号特征和运动特征，地面防空系统不能区分是战机还是UAV 或MALD 的假目标；同时，地面防空系统不进行威胁等级判定，只按照飞机或假目标到达的时间进行跟踪、打击。

3）防空单元对目标的处理时间，即从发现、跟踪，到目标-火力单元分配，以及到导弹发射、直至命中目标的总时间，是一个随机变量。设该随机变量服从参数为ζ 指数分布。

4）地面防空系统同时打击的目标数目有限，如果飞机或者UAV/MALD 的假目标数目达到地面防空系统处理目标数的上限，则后续到达的飞机或假目标直接不受威胁地通过防空系统。

上述模型实际上是一个带有拒绝功能的M/M/1/N 排队模型。其中，两个“M”表示目标到达间隔和防空系统“服务”目标的时间分布都是指数分布，“1”表示单一的防空系统，暂不考虑多个防空单元串并联的情形，“N”表示防空系统最多能够同时“服务”目标的数量。用有向图表示稳态时防空系统中目标数量状态的转移情况，如图1 所示。

图1 稳态时防空单元内目标数的变化情况

根据排队论的相关知识，用Pn（n=0，1，…，N）表示防空系统中有n 个目标时的极限概率，用防空系统内正在处理的目标的数目n=0，1，…，N 表示系统的状态。根据速率相等的原理，得到系统的平衡方程为［11］

飞机进入防空阵地，防空单元有空闲通道为飞机“服务”的概率为1-Pn，换言之，如果没有空闲通道，则飞机以概率1 成功通过该防空区域；设飞机在防空单元内停留的平均时间为τ，根据全概率公式，飞机在UAV 或者MALD 掩护下最终的生存概率PS可以表示为

结合式（8）～式（10），就可以评价不同的UAV/MALD 出动间隔下飞机的生存概率。

3 计算实例与分析

为了比较不同的UAV/MALD 投放速率，即不同ξ 下飞机的生存力，设=0.2，ζ=0.99，不同的N 下飞机被拒绝“服务”的概率，即防空单元饱和的概率（PN）以及飞机在非饱和情况下，通过防空区域的平均生存力随ξ 的变化关系，如图2 和图3 所示。

图2 战机被拒绝“服务”的概率

图3 被“服务”后的平均生存概率

由图2 和图3 可知，UAV/MALD 的投放速率越大，战机自身被防空单元拒绝“服务”的概率就越高；防空系统同时能够处理的目标数（N）越小，防空系统为目标拒绝“服务”的概率就越高。同时，UAV/MALD 的投放速率越大，防空单元的平均服务时间就会越长，与此对应的战机平均生存概率就越低；并且N 越大，战机的平均生存概率越低。

根据式（8），得到战机的生存概率与UAV/MALD的投放速率关系如图4 所示。

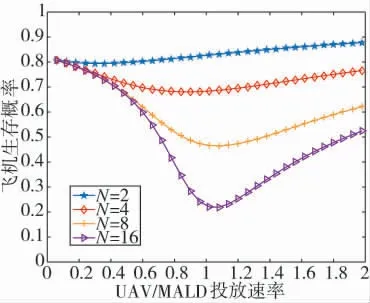
图4 战机在不同UAV/MALD 投放速率下的生存力变化

由图4 可知，战机的生存概率与UAV/MALD 的投放速率并不是单调递增的关系：当投放速率小于一定值时，投放速度越高、飞机生存力越低。表面上看这与直观上的感觉是相反的，实际上，这是因为此时防空单元处于不饱和的状态，且此时平均服务时间随着投放速率的增加而增加，平均服务时间越大，飞机的生存概率越低，所以会有生存力随着投放速率下降的区域。但是当投放速率大于一定值时，飞机的生存概率又随着投放速率的增加而增加，这是因为此时防空单元的作战通道趋于饱和，防空单元“拒绝”为战机提供服务的概率占了生存力的主要成分，作战通道数目越大，UAV/MALD 的支援作用就越小。

当ζ=0.49 时的飞机生存力随UAV/MALD 投放速率的变化关系如图5 所示。

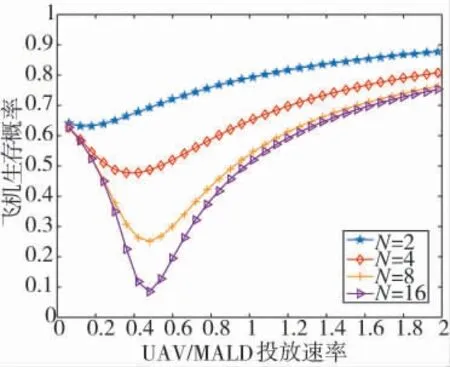
图5 不同投放间隔和等效暴露时间下飞机生存力

由图5 可知，当ζ 较小的时候（ζ 越小表明作战单元的“服务”速率越低，作战能力越弱），增加UAV/MALD 投放速率引起的战机生存力下降的区域也越小，其原因与前面分析的类似，在此不再赘述。

除了使用UAV 或MALD 等假目标掩护，飞机自身还可以采取电子对抗等措施，飞机采取对抗措施相当于降低式（1）中的值。当ζ=0.49，N=4 时，不同的下飞机生存概率随UAV/MLAD 投放速率的变化关系如图6 所示。

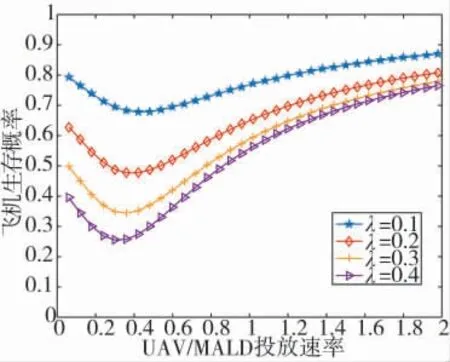
图6 不同投放间隔和暴露时间下飞机的生存力

由图6 可知，不同的λ 主要影响飞机生存力随UAV/MLAD 投放速率下降的区域，原因与之前分析的类似：当ξ 小于一定值时，增加ξ 会增加战机在防空单元内的平均驻留时间，λ 越大，飞机的生存概率越低；但是当ξ 大于一定值时，增加UAV/MLAD 的投放速率，可以让防空单元对战机的服务概率下降，从而飞机生存概率增加，但是此时λ 对战机生存概率的影响逐渐减小。

4 结论

在UAV/MALD 掩护下的飞机生存力主要受两个因素影响：一是飞机能否避免被防空系统探测、跟踪，即被防空系统拒绝“服务”的概率，二是如果飞机不可避免要接收防空系统的“服务”，则“服务”时间越长，战机的生存力越低。UAV/MALD 的掩护下的飞机生存力与UAV/MALD 的投放速率相关：当UAV/MLAD 的投放速率小于一定值时，战机实施对抗措施可以使战机的生存概率增加，但是增大投放速率反而引起防空单元平均服务时间上升，从而导致飞机生存概率的减少；当UAV/MLAD 的投放速率大于一定值时，战机实施对抗措施对飞机的生存概率贡献不大，此时增大UAV/MLAD 的投放速率可以降低防空单元对战机的“服务”概率，从而提升飞机的生存力。当、ζ 和N 都能确定时，可以通过求导的方式，确定最佳的UAV/MALD 投放速率，从而提高战机通过防空系统的概率。