关系代数在数据库实验教学的实践研究

谭毓银，李怀成，缪为民

（海南大学计算机与网络空间安全学院，海口570228）

0 引言

《数据库系统概论》[1]是我校信息类的专业必修课，其教学目标是向学生介绍数据库系统的基本概念及其构成，使学生掌握基本的关系数据库理论和典型关系数据语言SQL的编程。而关系代数运算及SQL语句用法是本课的重点和难点，SQL语句在实际的数据库开发运用中较灵活，其理论基础离不开对关系代数运算的理解[2-4]。

通过多年的教学，发现本课程涉及大量的理论讲解，教学基本采用教材所给的案例，每章节所举例题不尽相同，往往是东一个西一个，没有紧密的连贯性，缺乏统一的教学项目和案例设计，教学效果并不是很好，造成学员学习目的不明确，成就感不强，消极对待数据库原理知识和SQL语言的学习[5-7]。

在实验教学过程中，先以学生接触较多的学生选修课程模型为依托，合理设计教学案例，辅以图示分解教学，帮助学生掌握关系代数的运算，再讲解SQL语句基本用法，最后通过在实验中用SQL语句来实现关系代数运算，从而加深学生对SQL语句用法和关系代数运算的理解，为数据库查询打下坚实的基础。

1 关系代数运算

关系代数是一种抽象的查询语言，它用对关系的运算来表达查询，是处理关系数据库的重要数学基础，是关系数据操纵语言的一种传统表达方式。

关系代数运算按运算符的不同可分为传统的集合运算和专门的关系运算两类。传统的集合运算是二目运算，包括并、差、交、笛卡尔积4种运算；专门的关系运算包括选择、投影、连接、除运算等[1]。

设有学生关系Stud、学生关系Other、课程关系Course和选修关系StudCous，如表1-表4所示。下面的关系代数运算将对这四个关系进行运算。

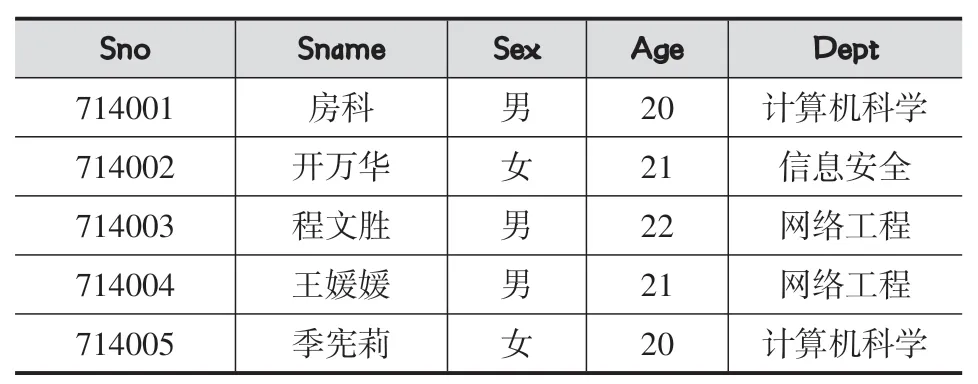
表1 Stud关系

表2 Other关系

表3 Stud关系

表4 StudCous关系

1.1 传统的集合运算

设关系R和关系S具有相同的目n（即两个关系都有n个属性），且相应的属性取自同一个域，t是元组变量，t∈R表示t是R的一个元组。

（1）并运算：将R与S合并，并且去掉重复元组后所构成的一个关系。

例1：将Stud与Other合并成SU关系，关系代数运算表达式为：

关系运算的结果如表5所示。因为Other关系中的“714002”“714004”所对应的元组已经存在于Stud关系中，所以合并后的关系只保留了一份。

表5 并运算后的SU关系

表6 交运算后的SN关系

（2）交运算：由既属于R又属于S的元组组成的新关系。

例2：将Stud与Other相交成SN关系，关系代数运算表达式为：

关系运算的结果如表6所示。因为Stud及Other关系中都有“714002”“714004”所对应的元组，所以相交后的关系只是由共同存在于这两个关系的元组所组成的新关系。

（3）差运算：由属于R而不属于S的所有元组组成，即在R中去掉R与S相同的元组。

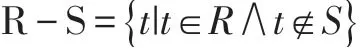
例3：将Stud与Other进行差运算，关系代数运算表达式为：

关系运算的结果如表7所示。因为Stud及Other关系中都有“714002”“714004”所对应的元组，所以差运算就是在Stud关系中去掉这两个相同元组后所组成的新关系。

表7 差运算后的SM关系

（4）笛卡尔积

这里的笛卡尔积严格地讲应该是广义的笛卡尔积。设有n元关系R及m元关系S，它们分别有p、q个元组，则关系R与S经笛卡尔积记为R×S，该关系是一个n+m元关系，元组个数是p×q，由R与S的有序组组合而成。即用R中的每个元组分别与S中的所有元组相结合组成一个新的关系。新的关系的属性个数为R与S属性个数之和，元组个数为R与S元组个数相乘积。

例4：将Stud与StudCous进行笛卡尔积运算，关系代数运算表达式为：

关系运算的结果如表8所示。

从表8中，可以看出，笛卡尔积实际上用左边关系的每一行分别与右边关系的所有行进行相乘（或相合并）。注意：笛卡尔积的全集在应用中是没有意义的。这里列出全集只是表示全部可能的组合而已，并不代表实际上有这么多可行的组合。笛卡尔积运算是为后面的连接、自然连接等做准备。

表8 笛卡尔积后的SCP关系

1.2 专门的关系运算

（1）选择：它是由关系R中满足逻辑条件的元组所组成的新的关系，记作：

逻辑条件F表示选择条件，它是一个逻辑表达式，取逻辑值“true”或“false”。

例5：查询关系Stud中Dept为“计算机科学”的信息。

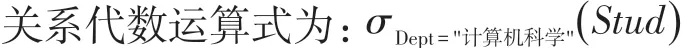
结果如表9所示。Stud关系原来有5个元组，而执行逻辑条件Dept=“计算机科学”运算后，只有2个元组满足条件。讲到这里，大家发现，选择运算是对关系进行元组（行）的选取，当然，如果有重复的行，还需要删除重复行后形成新的关系。

表9 选择运算后的关系

（2）投影：它是从R中选取出若干属性列，去掉重复的元组所组成新的关系，记作：

例6：查询关系Stud中Dept的信息。

关系代数运算式为：∏Dept( S tud)

结果如表10所示。R关系原来有5个元组，而投影结果消除了重复的部分元组，因此只有3个元组。讲到这里，大家发现，投影不仅取消了原关系中的某些列，而且还可能消去了某些元组，因为取消了某些属性列后，就可能出现重复行，就取消这些完全相同的行。所以投影是能够把一个关系的属性域变小的运算。

表10 投影运算后的关系

所以，有了投影、选择运算，我们就可以方便地找到一个关系内的任意行、列的数据。

（3）连接：它是从关系R和关系S的笛卡尔积中选取属性间满足一定条件的元组。记作：

其中，A和B分别为R和S上列数相等且可比的属性组，θ是比较运算符。因此，连接也称为θ连接。当θ为“=”时的连接运算称为等值连接，可以记为：

例7：查询每个学生及其选修课程的情况。关系Stud与关系StudCous进行Sno=S sn o的等值连接。关系代数运算式为：SW=StudSno=Ssno StudCous

结果如表11所示。该关系实际上是在表8关系中进行逻辑条件为“Sno=S sn o”的选择运算后得到的新关系，该运算大大减少了元组的个数。但是请大家注意Sno和S sn o属性对应的值是一样的。假如我们把S sno属性名改为Sno，就将会变成自然连接。

表11 等值连接后的SW关系

（4）自然连接：自然连接是一种特殊的等值连接。它要求：①两个关系要有公共的属性域；②通过公共域的相等值进行连接。记作：

例8：假设我们将关系StudCous中的S sn o属性改名为Sno，把关系Stud与改名后的关系StudCous进行自然连接。

关系代数运算式为：SP=Stud⋈StudCous

结果如表12所示。该关系和表11的关系很类似，只是少了Sno（S sn o已经更名为Sno）的同名属性列。即自然连接是在等值连接的基础上，消除两个关系的公共属性域的连接。

表12 自然连接后的SP关系

一般的连接操作是从行的角度进行运算，但自然连接还需要取消重复列，所以是同时从行和列的角度进行运算。

（5）除运算

设关系R除以关系S的结果为T，则T包含所有在R但不在S中的属性及其值，且T的元组与S的元组的所有组合都在R中。记作：

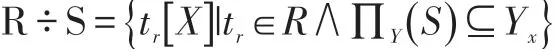
这个定义是教材给出的。在这几种运算中，除法运算复杂、抽象，是教学环节中的难点问题，学生理解起来比较困难[8]。如何来讲解除法运算呢？

我们先对StudCous关系的S sn o和Cno属性做投影操作，即：SCNO=∏Ssno,Ccno(StudCous)，得到的关系SCNO如表13所示。再对Course关系的Cno属性做投影操作，即：CNO=∏Cno(Course)，得到的关系CNO如表14所示。那么SCNO÷CNO得到的关系SSNO如表15所示。这实际上就是：

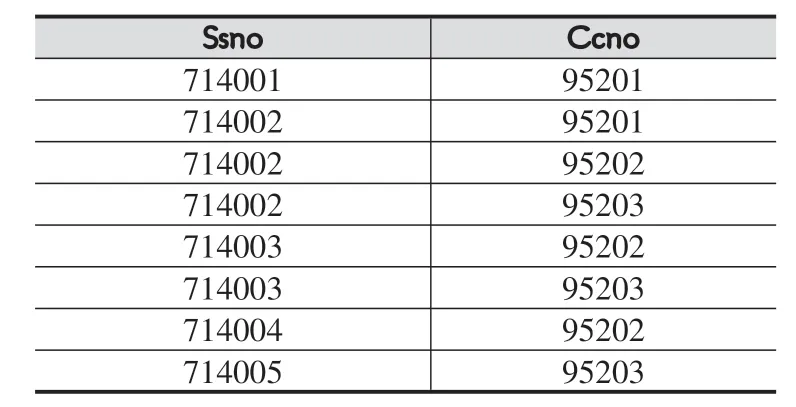
表13 SCNO关系

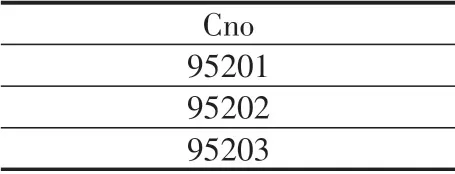
表14 CNO关系

表15 SSNO关系

例9：查询选修了所有课程的学生姓名。

2 SQL中关系代数运算的实现

2.1 SQL简介

SQL（Structured Query Language）是关系数据库的标准语言，也是一个通用的、功能极强的关系数据库语言。其主要特点包括：综合统一、高度非过程化、面向集合的操作方式、以同一种语法结构提供多种使用方式、语言简洁、易学易用等。

2.2 数据查询

数据查询是数据库的核心操作。SQL提供了SELECT语句进行数据查询，该语句具有灵活的使用方式和丰富的功能[10]。其一般格式为：

基本的工作原理：FROM子句先被执行，通过FROM子句获得一个虚拟表，然后通过WHERE子句从虚拟表中获取满足条件的记录，生成新的虚拟表。将新虚拟表中的记录通过GROUP BY子句分组后得到更新的虚拟表，而后HAVING子句在最新的虚拟表中筛选出满足条件的记录组成另外一个虚拟表中，SELECT子句会将指定的列提取出来组成更新的虚拟表，最后ORDER BY子句对其进行排序得出最终的虚拟表。通常这个最终的虚拟表被称为查询结果集[11]。

2.3 SQL实现

每种关系运算在SQL中都有对应的实现，Union、Intersect、Except分别对应集合运算中的并、交、差运算，但在SQL Server中不支持Intersect、Except运算符的使用。本实验通过在SQL Server 2008环境下实现关系代数的各种运算（例1-例9），使学生在感性上进一步认识关系代数在数据库中的应用，从而更深刻地理解了关系代数运算和更熟练地掌握了SQL语句的用法[12]。

例1中并运算的SQL语句

Select*from Stud Union Select*from Other

例2中交运算的SQL语句

Select Stud.*from Stud,Other Where Other.Sno=Stud.Sno）

例3中差运算的SQL语句

Select*from Stud Where Sno not in（Select Sno from Other）

例4中笛卡尔积运算的SQL语句

Select*from Stud,StudCous

例5中选择运算的SQL语句

Select*from Stud Where Dept=^'计算机科学'例6中投影运算的SQL语句

Select Distinct Dept from Stud

例7中等值连接运算的SQL语句

Select*from Stud,StudCous Where Stud.Sno=Stud⁃Cous.Ssno

例8中自然连接运算的SQL语句

Select*from Stud,StudCous Where Stud.Sno=Stud⁃Cous.Sno

例9的SQL语句，除运算

Select Sname From Stud Where not exists

（Select*From Course Where not exists

（Select*From StudCous Where Stud.Sno=StudCous.Ssno

And Course.Cno=StudCous.Ccno

）

）

注意，在做连接查询时，至少涉及两个以上的表，用到的关系运算为笛卡尔积或连接或自然连接。但它们都是在笛卡尔积的基础上所进行的操作。

最后，我们利用教材中的一个例子，引导学生思考查询优化的步骤，激发学生对查询优化的兴趣。

例3.51查询选修了95203的课程且成绩在80分以上的所有学生的学号和姓名。

Select Stud.Sno,Stud.Sname From Stud,StudCous

Where Stud.Sno=StudCous.Ssno and StudCous.Score>=80

对应的关系代数运算表达式为：

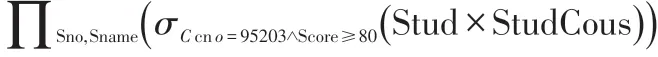
从这个表达式中，先是关系Stud与StudCous做笛卡尔积运算，然后再选取满足逻辑条件为σCcno=95203∧Score≥80的元组组成一个虚拟表关系，再对该关系的Sno，Sname列进行投影运算，如果有重复行，去掉重复行后组成查询结果集。在课堂讲解上，就用表8笛卡尔积运算的结果来演示，让学生知道会产生大量的元组及属性，然后引出优化的问题。

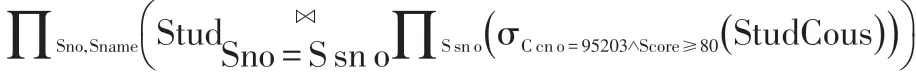
该查询优化的思想是先从StudCous中选取出σCcno=95203∧Score≥80的元组形成一个虚拟表关系，再和Stud中满足连接条件的元组进行连接得到最终的结果关系。

由此，一步步引导学生进行查询优化的提出，在加强学生关系代数的学习的同时，也为后续学生学习SQL查询优化指引了一个方向。

3 结语

关系代数运算是数据库原理课中较为抽象的内容，是SQL查询的理论基础。如果以纯理论教学为主，学生不能真正理解关系代数运算，也就不可能写出优异的SQL语句。这就要求教师在设计教学案例时，能够纵览全局，设计前后统一、连贯性强的教学项目案例，将能帮助学生快速理解该知识点乃至该门课程起到至关重要的作用，同时也能提高学生的实验动手能力。由于该课程在近几年中一直是我校的教学示范课程，2018年3月该课程成为“第二批海南省高校精品在线开放课程立项建设课程”。