高考圆锥曲线离心率问题的基本解析
2021-08-05肖琳婧
肖琳婧
(云南师范大学数学学院 650000)
一、考题分析
离心率是圆锥曲线的一个重要基本量,求圆锥曲线离心率的值或范围的问题也是圆锥曲线中的重点,由于这类问题综合性比较强,能够更好地体现学生的思维能力以及直观想象、逻辑推理、数学运算、数学抽象等核心素养,因此备受高考命题者的关注.
分析2019年高考试题对圆锥曲线知识点考查的情况,全国卷很明显加强了对圆锥曲线的考查力度,试题的题序都在后移,如选择题或填空题文科Ⅰ、Ⅱ卷在第12题,理科Ⅰ卷在第16题.命题者将圆锥曲线和直线结合在一起,普遍把解析几何作为压轴题来考查,改变了传统以函数与导数为压轴题的做法.无论是全国统一命题还是省自主命题,选择题或填空题主要考查圆锥曲线的定义(第一定义、第二定义)、标准方程和简单的几何性质,而解答题的综合性比较强,切入容易深入难.根据对2019年考题的侧重分析,结合新课程的教学理念,预测2020年高考命题者还是会将圆锥曲线的考题放在压轴位置.
二、例题解析
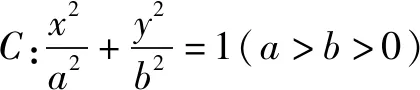
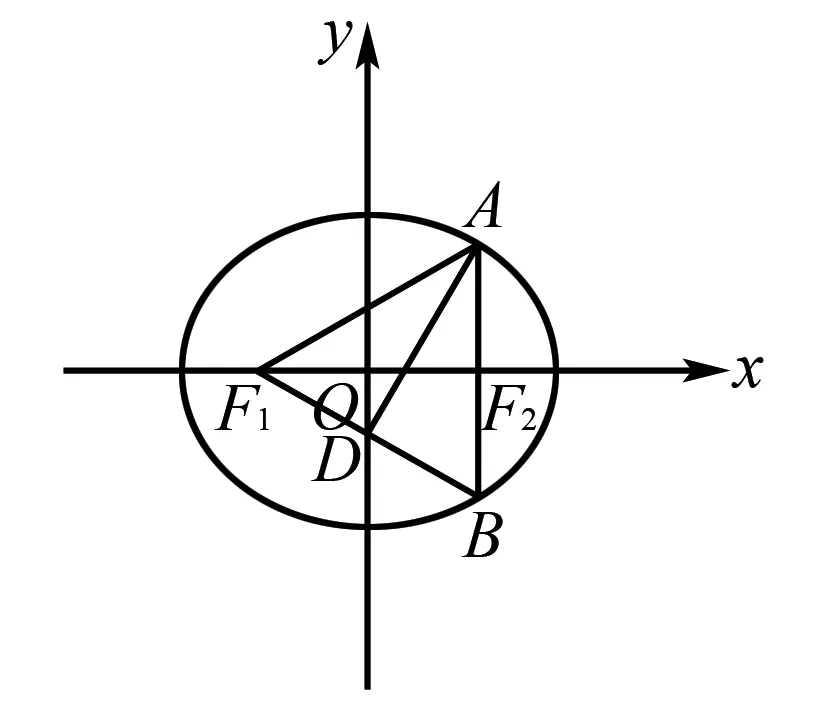
图1
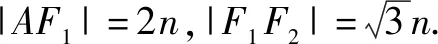
注:用几何关系和椭圆的定义得到a,c的关系,进而得到离心率.
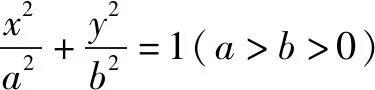
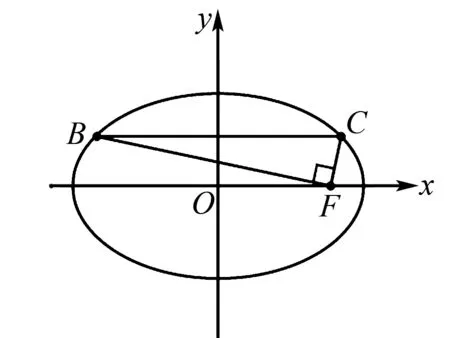
图2
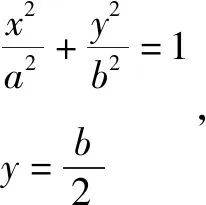
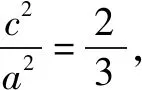
注:用代数关系(向量的坐标表示)找到a,c的关系,进而得到离心率.
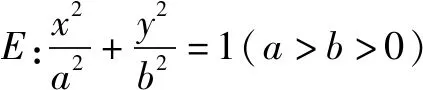
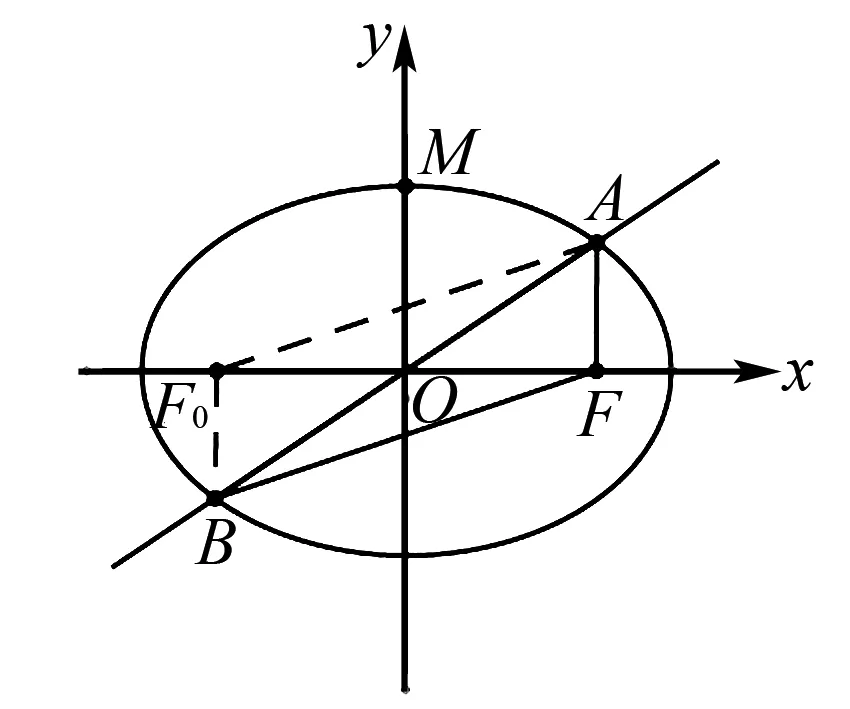
图3
解取左焦点F0,连接F0A,F0B,则四边形AFBF0是平行四边形.
因为|AF|+|BF|=4,所以|AF|+|AF0|=2a=4,即a=2.
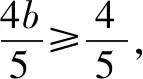
注:先求得a,再利用点到直线的距离公式得到b的取值范围,进而得到离心率的取值范围.
三、基本策略
1.求椭圆离心率或取值范围的方法
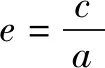
2.求离心率值的常用方法
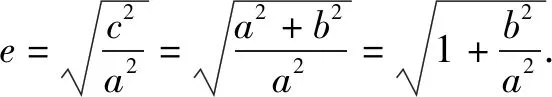
(2)列出含有a,b,c的齐次方程(或不等式),借助于b2=c2-a2消去b,然后转化成关于e的方程(或不等式)求解.
四、解题启示
纵观解析几何试题,题目中一般未给出图形,解题要求解题者正确画出图形,从图形中推理出几何或者代数关系,利用几何直观助力问题思考,不断提高解题者逻辑推理和直观想象的能力.圆锥曲线的定义是圆锥曲线的根源,某些问题的突破口就是回归定义,如例1、例3运用了椭圆的定义.解析几何研究的是几何问题,研究过程中总离不开图形,同时在解决问题时要注意是否能够灵活运用向量、平面几何、三角函数等知识简化几何关系和代数运算,综合考虑问题,养成良好的思维习惯.
如何在解题过程中落实学生的核心素养,这给一线教师的教学也提出了较高的要求.学生在学习圆锥曲线离心率的过程中一是要具备定义意识,定义是对数学问题解决的原动力,所以圆锥曲线的定义,也是对圆锥曲线本质属性的真实反馈,是圆锥曲线的灵魂所在,在解决问题过程中,可以对其定义进行灵活运用.二是方程意识,方程思想在解决数学问题时,寻找已知与未知之间的等量关系,构造方程或方程组,通过求解方程完成未知向已知的转化,其在圆锥曲线离心率问题研究的过程中也发挥了重要的作用.因为有些几何问题表面上看起来与代数问题无关,但是要利用代数方法——列方程来解决,学生在求解过程中要善于挖掘隐含条件,具备方程的思想意识.三是平面几何意识,在对几何问题进行解析的过程中,需要将数量关系作为研究基础,这种方式不仅可以为学生进行思维的简化,同时还可以对解题过程进行优化.培养学生的数学意识,有助于对学生数学抽象、逻辑推理、数学运算、直观想象等核心素养的落实.
