由一道课本练习题引发的多角度探究
2021-08-05贺凤梅
贺凤梅
(新疆伊犁州巩留县高级中学 835400)
一、问题展示
人教A版数学选修2-1第72页练习第题:过点M(2,0)作斜率为1的直线l,交抛物线y2=4x于A、B两点,求|AB|.
二、总体分析
三、试题解答
1.利用两点间的距离公式求解
分析这种解法的的关键是联立直线与抛物线的方程组成的方程组,求出方程组的公共解,即得两交点的坐标,再代入两点间的距离公式求解,便可以得出弦长.
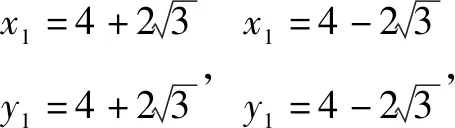
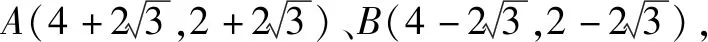
由两点间的距离公式得
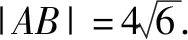
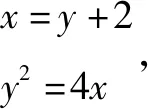
整理得y2-4y-8=0,
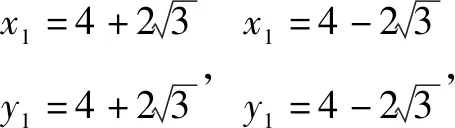
评注解法1和解法2的解题启示是:运用两点间的距离公式求弦长时,根据直线的特点,可以灵活选择消去或消去,当然是以方便求解为原则.这种方法学生比较容易想到,通过此种求解过程,可以锻炼和提高学生的计算能力.
2.利用弦长公式求解
分析这种解法的的关键是联立直线与抛物线的方程组成的方程组,消去x或者消去y,由根与系数的关系得出两根之和以及两根之积,代入相应的弦长公式,便可以求出弦长.
解法3由解法1,有x2-8x+4=0,由根与系数的关系得x1+x2=8,x1x2=4,直线斜率k=1,再代入弦长公式
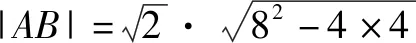
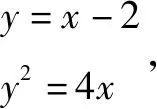
由直线y=x-2方程变形得x=y+2,
代入抛物线y2=4x方程,消去x,得
y2=4(y+2),
整理得y2-4y-8=0,
可知y1、y2是以上关于y的方程的产根,由根与系数的关系得y1+y2=4,y1y2=-8,
代入对应的弦长公式

评注解法3和解法4比较而言,学生比较容易想到的是解法3,如果选择使用弦长公式求解,需要给学生讲清楚的是联立方程得到的方程组消元时,同样需要根据直线方程的特点,以方便求解为前提条件.
3.构造直角三角形,由边角关系求解
分析这种解法的关键是根据题目条件,数形结合,找到直线与抛物线两交点的纵坐标(或横坐标)、弦长以及直线倾斜角之间的联系,在所构造的直角三角形中求解完成.
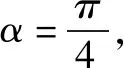
由解法4得
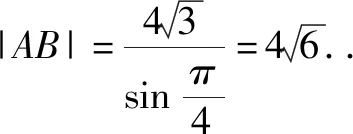
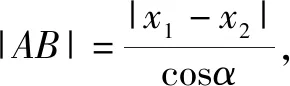
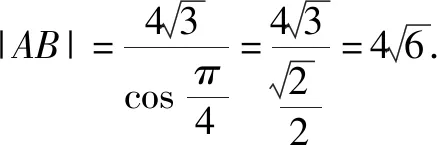
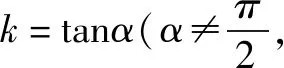
4.利用直线的参数方程求解
分析这种求解方法的关键是利用直线参数方程的几何意义,当直线参数方程为标准型时,将直线的参数方程中的x和y代入抛物线方程,得到关于t的一元二次方程,借助根与系数的关系(韦达定理),以及|AB|=|t1-t2|,可顺利求解完成解答.
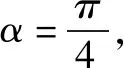
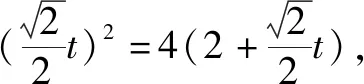
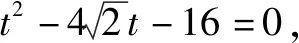
设A、B两点的参数分别为t1、t2,由参数的几何意义得
评注用此法求弦长时,一定要明确直线参数方程中是否具有几何意义.若具有几何意义,可直接求解;若不具有几何意义,一定要进行变形,求出具有几何意义的直线参数方程,方可求解.
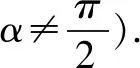
变式将直线l所经过的点改为(1,0),即经过抛物线的焦点F,这道题就是人教A版选修2-1课本第69页的例4.
现作为解法8和解法9简述如下:
5.利用抛物线的定义求解
分析此解法的关键是直线经过抛物线的焦点,根据抛物线的定义,抛物线上的点到焦点的距离等于到准线的距离,转化求解即可完成.
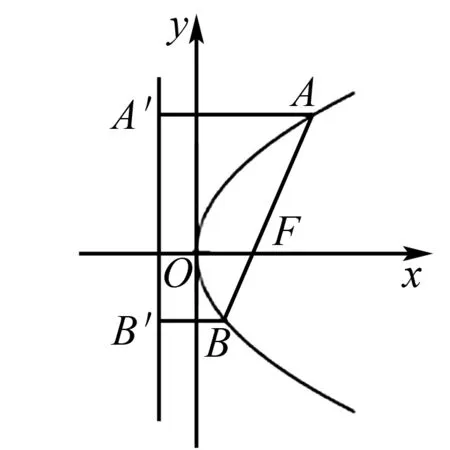
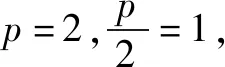
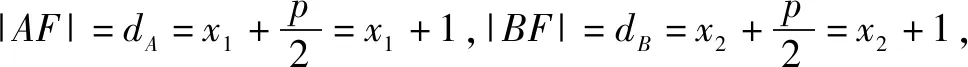
|AB|=|AF|+|BF|=dA+dB
=x1+x2+p=x1+x2+2
直线方程为y=x-1,
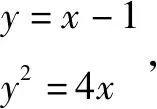
x2-6x+1=0,由根与系数的关系x1+x2=6,
于是|AB|=x1+x2+2=6+2=8.
评注此法只要求出两点A、B的横坐标之和x1+x2,就可以求出弦长|AB|.
6.利用抛物线的焦点弦求解
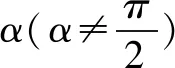
解法9由于直线经过抛物线y2=4x的焦点F,所以可以由抛物线的焦点弦公式求解.

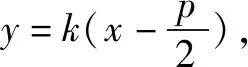
代入抛物线方程中y2=4x,
化简并整理得
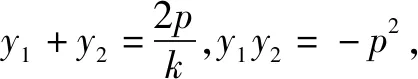
由弦长公式
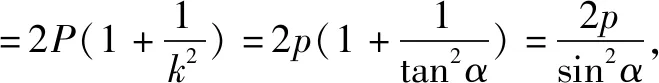
因此,利用焦点弦公式求得
评注此解法在高三总复习的一些参考资料上出现过,原则上这种方法做解答题时需要证明结论的正确性才可以使用.不过做选择题或填空题还是比较方便和快捷的.
四、解后反思
这道练习题和相关联的例题是一道容易题,但却是一道好题.它蕴含着丰富的数学思想方法,考查了学生的运算求解能力,数形结合思想,以及化归转化等方法.在平常的解题中,要引导学生运用所学知识,多角度多方位进行思考,从而获取不同的解法.在平时的解题教学中,一定要跳出定势思维的束缚,提倡一题多解,可以从代数方面进行思考和突破,也可以从几何方面入手,运用数形结合来解决.当然,一定要引导学生重视教材,培养学生研究教材的兴趣,让学生清楚地认识到教材的重要性,同时培养学生的探索精神,还能达到触类旁通、举一反三的效果.
